Понятие регрессионного анализа. Линейный и нелинейный регрессионный анализы. Линейное и нелинейное уравнения регрессии

1. Министерство культуры российской федерации федеральное государственное бюджетное образовательное учреждение высшего образования

МИНИСТЕРСТВО КУЛЬТУРЫ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ КИНО И
ТЕЛЕВИДЕНИЯ»
ПРЕЗЕНТАЦИЯ
По дисциплине «Приемы и методы обработки экспериментальных данных»
Выполнила: Студентка гр. 3134
Петракова А.П.
Санкт-Петербург
2025

2.

Понятие регрессионного анализа. Линейный и нелинейный
регрессионный анализы. Линейное и нелинейное уравнения регрессии.
Регрессионный анализ — это статистический метод исследования зависимости между
зависимой (целевой) переменной и одной или несколькими независимыми (объясняющими)
переменными. Он широко применяется в экономике, биологии, медицине, машинном обучении
и других областях для прогнозирования и анализа данных.

3.

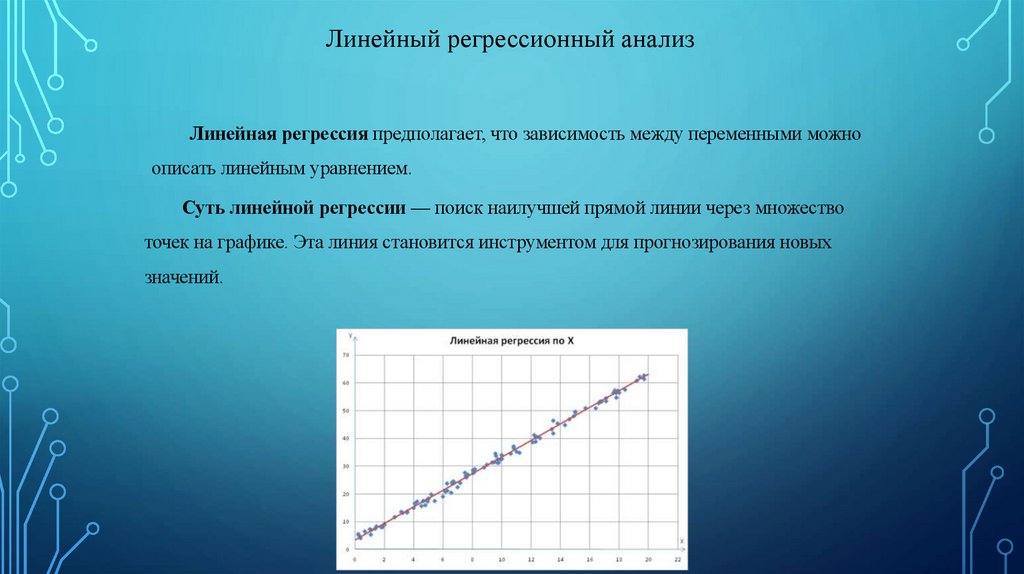
Линейный регрессионный анализ
Линейная регрессия предполагает, что зависимость между переменными можно
описать линейным уравнением.
Суть линейной регрессии — поиск наилучшей прямой линии через множество
точек на графике. Эта линия становится инструментом для прогнозирования новых
значений.

4.

Простая линейная регрессия
Множественная линейная регрессия
Простая линейная регрессия — статистический метод, позволяющий предсказывать
значения зависимой переменной Y по значениям независимой переменной X.
Уравнение имеет вид:
y=β0​+β1​x+ε
Множественная линейная регрессия — это статистический метод, позволяющий
анализировать взаимосвязь между зависимой переменной и несколькими независимыми
переменными. В отличие от простой линейной регрессии, этот метод позволяет работать
с несколькими факторами влияния одновременно, существенно повышая точность
прогнозов и глубину анализа.
Уравнение принимает вид:
y=β0​+β1​x1​+β2​x2​+⋯+βnxn​+ε

5.

Пример линейной регрессии
Зависимость выходного напряжения (y) от входного тока (x)
в транзисторном каскаде:
Входной ток x (мА)
Выходное напряжение y (В)
Уравнение регрессии:
1.0
2.1
y=2.02x+0.05
2.0
4.3
3.0
6.0
4.0
8.2
5.0
10.1

6.

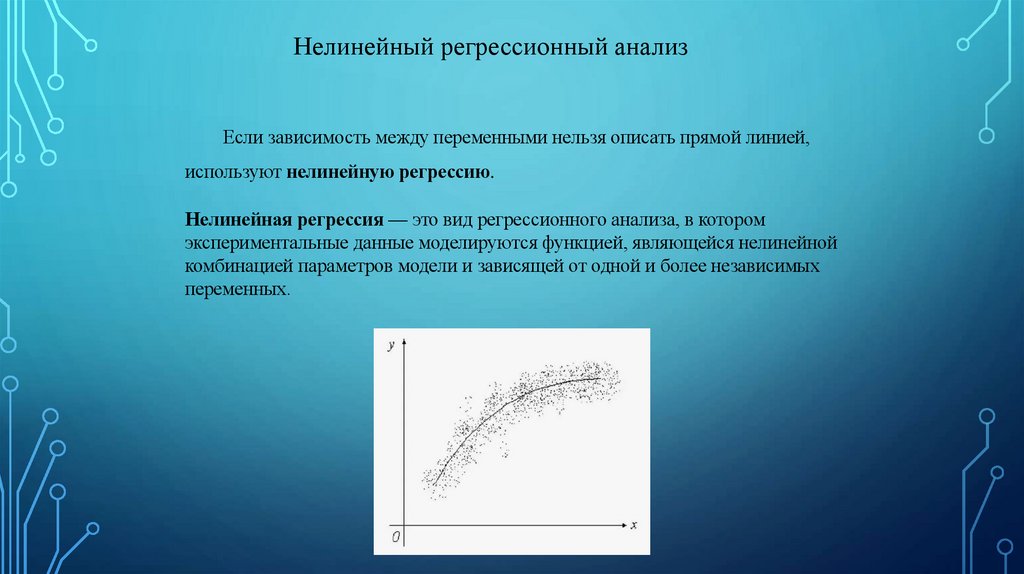
Нелинейный регрессионный анализ
Если зависимость между переменными нельзя описать прямой линией,
используют нелинейную регрессию.
Нелинейная регрессия — это вид регрессионного анализа, в котором
экспериментальные данные моделируются функцией, являющейся нелинейной
комбинацией параметров модели и зависящей от одной и более независимых
переменных.

7.

Виды нелинейных моделей
1. Полиномиальная регрессия (например, квадратичная):
y=β0+β1x+β2x^2+ϵ
2.Экспоненциальная регрессия:
y=β0e^β1x +ϵ
3.Логарифмическая регрессия:
y=β0+β1ln(х)+ϵ
4.Логистическая регрессия (для классификации):
y=1/1+e^−(β0+β1x)

8.

Пример нелинейной регрессии
Моделирование зависимости коэффициента гармоник
(THD) усилителя от входного напряжения
Входное напряжение (В)
THD (%)
0.5
0.1
1.0
0.5
1.5
1.2
2.0
2.8
2.5
5.0
Нелинейная модель (квадратичная регрессия):
THD=0.05+0.1UBвх+0.5U2вх
Нелинейная модель точнее описывает реальные
характеристики усилителя, чем линейная аппроксимация,
особенно в области больших сигналов.

9.

Нормальный случайный процесс и его математическое
описание
Нормальный случайный процесс — это процесс, у которого любая конечная
совокупность его сечений (значений в различные моменты времени) имеет совместное
нормальное (гауссовское) распределение.
Пример : Тепловой шум в резисторе
Когда ток проходит через резистор, из-за хаотичного движения электронов возникает
шум. Этот шум можно описать нормальным случайным процессом с нулевым средним
(так как шум симметричен) и определённой дисперсией (мощностью шума).

10.

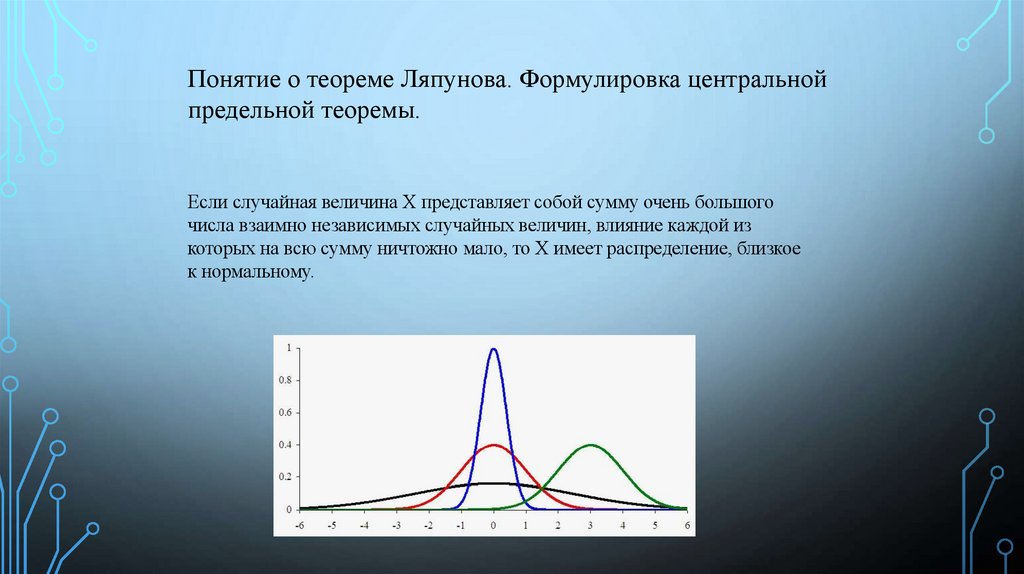
Понятие о теореме Ляпунова. Формулировка центральной
предельной теоремы.
Если случайная величина X представляет собой сумму очень большого
числа взаимно независимых случайных величин, влияние каждой из
которых на всю сумму ничтожно мало, то X имеет распределение, близкое
к нормальному.

11.

Свойства нормального случайного процесса

12.

Математическое описание
Плотность вероятности нормального случайного процесса

13.

Математическое описание
Математическое ожидание и автокорреляционная функция

14.

Математическое описание
Двумерная плотность распределения вероятностей

15.

Заключение
Нормальный случайный процесс является фундаментальной моделью в
радиотехнике благодаря своим удобным математическим свойствам и
широкой применимости для описания случайных сигналов и шумов. Его
статистические характеристики позволяют эффективно решать задачи
фильтрации, обнаружения сигналов и анализа помех.

16.

Спасибо за внимание!