Регрессионный анализ

1.

Регрессионный анализ

2.

Регрессионный анализ – это статистический метод
исследования зависимости величины Y от величин
Х j ( j 1, k ) .
Задачи регрессионного анализа:
установление
формы
зависимости
переменными (спецификация),
определение параметров
(параметризация),
выбранного
между
уравнения
анализ качества уравнения (верификация) и проверка
адекватности уравнения эмпирическим данным,
определение
значений).
неизвестных
значений
(прогноз

3.

Если каждому значению X соответствует свое
значение M(Y|X), то зависимость
M (Y | Х ) f ( Х )
называется функцией регрессии Y на Х.
При этом X называется экзогенной, Y – эндогенной.
При рассмотрении зависимости
двух переменных говорят о парной регрессии:
M (Y | Х ) f ( Х )
нескольких переменных говорят о множественной
регрессии
M (Y | Х 1 , Х 2 ,..., Х k ) f ( Х 1 , Х 2 ,..., Х k ) .

4.

Реальные значения Y не всегда совпадают с
M (Y | Х ) .
Поэтому
фактическая
зависимость
дополняется случайной величиной ε.
Статистическую модель вида:
Y f (Х )
или
Y f ( Х1 , Х 2 ,..., Х k )
называют регрессионными моделями (уравнениями).
В зависимости от вида функции f ( Х ) модели
делятся на линейные и нелинейные.

5.

Спецификация уравнения регрессии.
В случае парной регрессии – графический анализ
реальных статистических данных (наблюдений).
Линейная зависимость Yˆ 0 1 X .

6.

Квадратичная зависимость:
2
ˆ
Y 0 1 X 2 X

7.

Степенная зависимость
Yˆ X 1
0

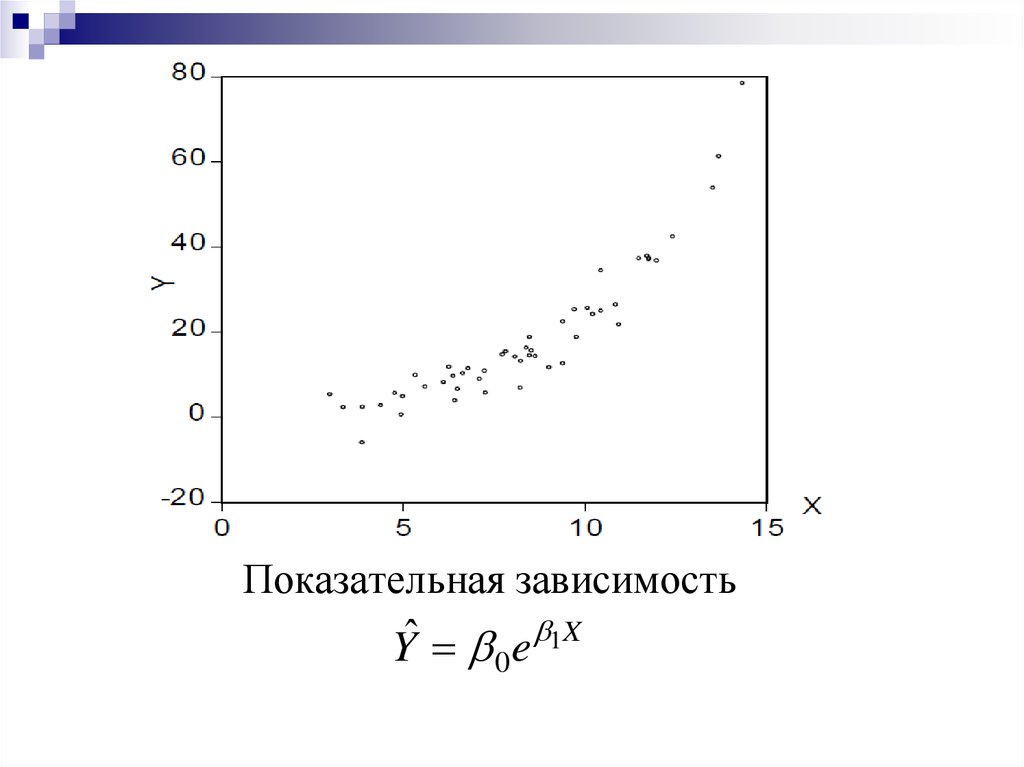
8.

Показательная зависимость
1X
ˆ
Y e
0

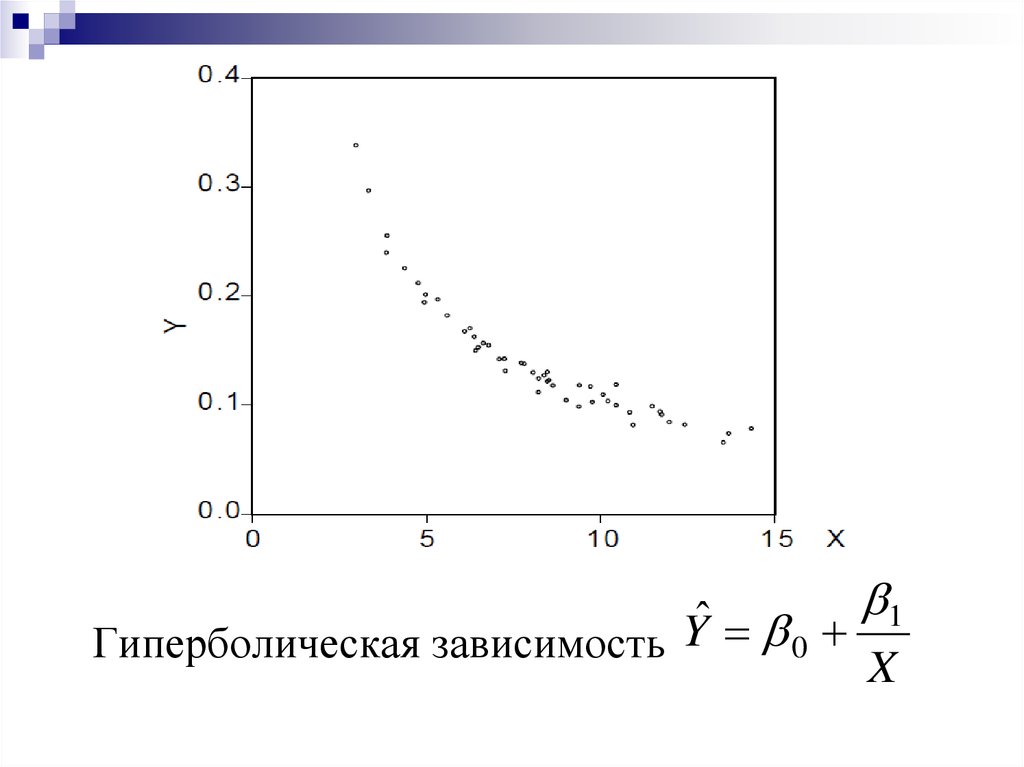
9.

ˆ
Y
0
Гиперболическая зависимость
1
X

10.

X и Y независимы

11.

Классическая модель
парной линейной регрессии.

12.

Общий вид модели парной линейной регрессии:
Y 0 1 X , где
β0 –свободный член уравнения (среднее значение Y при
условии, что X=0),
β1– коэффициент регрессии, характеризует изменение
среднего значения переменной Y, при изменении значения X
на единицу своего измерения:
если 1 0 – переменные X и Y положительно
коррелированные,
если 1 0 – отрицательно коррелированны.
εi – случайная составляющая.

13.

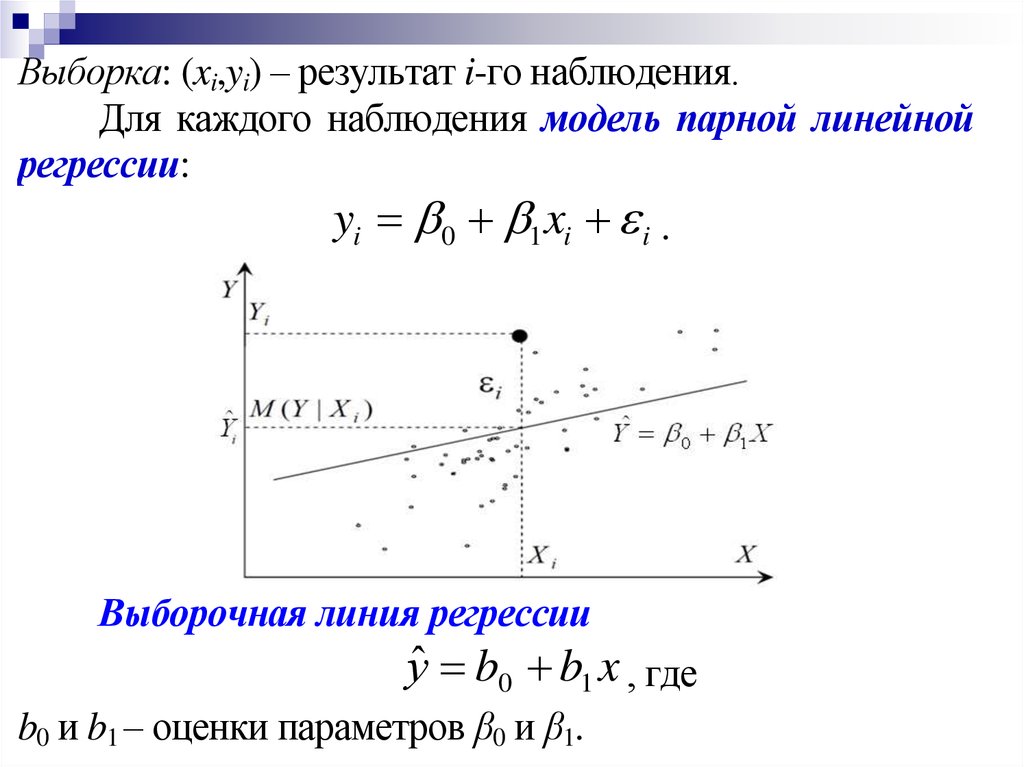
Выборка: (xi,yi) – результат i-го наблюдения.
Для каждого наблюдения модель парной линейной
регрессии:
yi 0 1xi i .
Выборочная линия регрессии
уˆ b0 b1 x , где
b0 и b1 – оценки параметров β0 и β1.

14.

КЛАССИЧЕСКИЙ (ОБЫЧНЫЙ)
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
(МНК)

15.

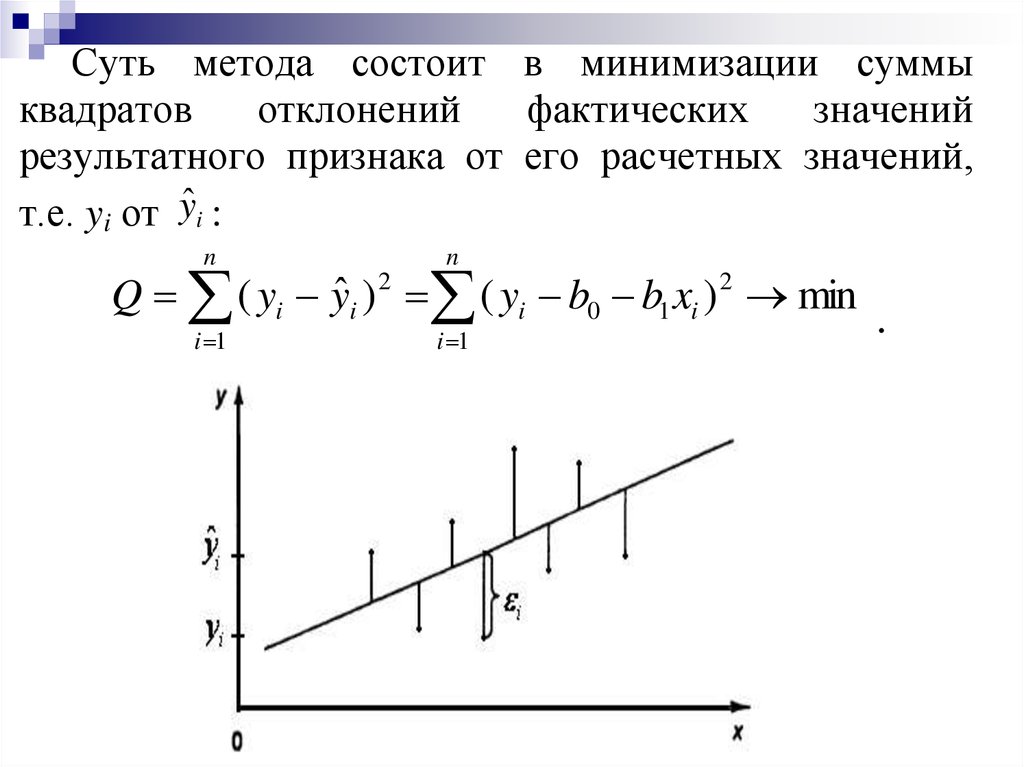
Суть метода состоит в минимизации суммы
квадратов
отклонений
фактических
значений
результатного признака от его расчетных значений,
т.е. yi от yˆ i :
n
n
i 1
i 1
2
2
ˆ
Q ( yi yi ) ( yi b0 b1 xi ) min
.

16.

Найдем частные производные Q и приравняем их к
нулю:
n
Q
b 2 ( yi b0 b1 xi ) 0;
0
i 1
n
Q
2 ( yi b0 b1 xi ) xi 0.
b1
i 1
Получим систему нормальных уравнений:
b0 b1 x y
nb0 b1 xi yi
2
2
или
b
x
b
x
x
y
0 i 1 i
i i
b0 x b1 x xy

17.

Решая систему, получаем:
b0 y b1 x ,
b1
xy x y
x x
2
х
х
у
i
;
n
уi
n
2
cov( X , Y )
,
sx2
x
2
; xy
х
2
i
n
хi yi
n
;
.

18.

По полученному уравнению регрессии
yˆi b0 b1 xi
получают расчетные (прогнозные) значения
переменной у для каждого i наблюдения, т.е.
уˆ i ( хi ) .
Величина b1 – выборочный коэффициент
регрессии Y no X, который показывает, на
сколько единиц в среднем изменяется
переменная Y при увеличении переменной X на
одну единицу.

19.

МАТРИЧНАЯ ФОРМА ЗАПИСИ
ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

20.

Матричная форма модели:
Y X ,где
y1
Y ... – вектор значений зависимой;
yn
0
– вектор неизвестных параметров;
1
1
... – вектор случайных ошибок.
n

21.

1 x1
X ... ... 1 xn
матрица
значений
независимых
переменных размерности.
Оценка модели по выборке
Yˆ Xb , где
b0
b
b1
-
вектор
оценок
параметров.
Решение в матричной форме:
1
b (X X ) X Y .
T
T
неизвестных

22.

ОСНОВНЫЕ ПРЕДПОСЫЛКИ
МНК

23.

Условия Гаусса – Маркова.
1. i (i 1, n) (или yi) есть величина случайная,
а объясняющая переменная хi – величина
неслучайная: cov( i , X i ) 0 .
2. M ( i ) 0 для всех наблюдений Y.
2
D
(
)
const для всех наблюдений Y.
3.
i
Это
условие
называется
условием
гомоскедастичности.
В матричной форме:
D( i ) 2 E n , где
Еn — единичная матрица n-го порядка.

24.

4. i и j независимы в любых двух наблюдениях:
cov( i , j ) М ( i , j ) 0 i j , т.е. отклонения регрессии
не коррелируют:
0, i j
cov( i , j ) 2
.
,
i
j
Матричная форма записи предпосылки:
T
2
cov( ) En , где
E n – единичная матрица n–го порядка, а cov( T ) –
ковариационная матрица возмущений
2 0
2
0
cov( T )
... ...
0
0
0
... 0
.
... ...
2
...
...

25.

Модель
парной
линейной
регрессии,
построенная с учетом условий Гаусса–Маркова
называется классической регрессионной моделью.
Если с условиями Гаусса – Маркова также
предполагается
нормальность
распределения
случайного члена:
i ~ N (0; 2 )
2
~
N
(
0
;
E n ) ),
(если – вектор возмущений, то
то модель называется классической нормальной
регрессионной моделью.

26.

СВОЙСТВА ОЦЕНОК МНК
Несмещенность оценки означает, что M ( ) 0 .
Вектор b – несмещенная оценка вектора : M (b) .
Оценки считаются эффективными, если они
характеризуются наименьшей дисперсией.
Вектор b – наиболее эффективная оценка вектора
, т.е. обладает наименьшей дисперсией:
2 (b) min .
Состоятельность
оценок
характеризует
увеличение их точности с увеличением объема
выборки.
Вектор b – состоятельная оценка вектора :
lim b j β j .
n

27.

ОЦЕНКА КАЧЕСТВА (ВЕРИФИКАЦИЯ)
МОДЕЛИ

28.

Качество модели регрессии связывают с
адекватностью
(или
соответствия)
модели
эмпирическим данным.
Проверка адекватности модели регрессии – на
основе анализа остатков - ei .
Качество модели регрессии оценивается по
следующим направлениям:
1) проверка общего качества уравнения регрессии;
2) проверка значимости уравнения регрессии;
3) проверка
статистической
значимости
коэффициентов уравнения регрессии;
4) проверка выполнения предпосылок МНК.

29.

ПРОВЕРКА ОБЩЕГО КАЧЕСТВА
УРАВНЕНИЯ РЕГРЕССИИ

30.

Вычисляют коэффициенты, по которым
делаются выводы об ее адекватности и
точности.
1. Качество парной линейной регрессии
определяется
с
помощью
выборочного
коэффициента парной линейной корреляции
– показателя близости наблюдений к линейной
регрессии:
r
xy x y
x x y y
2
2
2
2
cov( X , Y )
.
sx s y

31.

2. Коэффициент детерминации – наиболее
эффективная
оценка
адекватности
регрессионной модели:
2
ˆ
(
y
y
)
i i
Qост
R 1
1
2
,
где
Q
(
y
y
)
общ
i
2
2
ˆ
Qост ( yi yi ) – сумма квадратов остатков.
Qобщ ( yi y ) 2 – общая сумма квадратов.
2
показывает на сколько процентов
вариация результативного признака Y учтена в
модели и обусловлена влиянием на него фактора
Х в общем объеме вариации.
R

32.

Свойства коэффициента детерминации.
1. 0 R 1 .
2
R
0 – вывод о независимости Y и X.
2.
2
3. R 1 – вывод о наличии функциональной
линейной зависимости между переменными Y и
X.
2
0
R
1 – чем ближе R 2 к 1, тем лучше качество
4.
подгонки кривой к нашим данным, тем точнее Y.
2

33.

3. Для оценки точности прогноза используются
характеристики: несмещенная оценка остаточной
дисперсии, стандартная ошибка остатков и средняя
относительная ошибка аппроксимации.
Несмещенная оценка остаточной дисперсии:
2
Qост
1
2
S
( yi уˆ i )
,
n 2
n 2
2
ˆ
Qост ( yi yi )
– сумма квадратов остатков.
2
ˆ
Величину S S
называют стандартной
ошибкой остатков.
Чем меньше значения этих характеристик, тем
выше точность модели.

34.

Средняя
относительная
ошибка
аппроксимации – среднее относительное
отклонение расчетных значений зависимой
переменной yˆ i от фактических значений yi :
1 n yi yˆ i
100%
n i 1
yi
Если средняя ошибка аппроксимации
составляет менее 6–7%, то качество модели
считается хорошим.
Максимально
допустимым
значением
данного показателя считается 12-15%.

35.

ПРОВЕРКА ЗНАЧИМОСТИ
УРАВНЕНИЯ РЕГРЕССИИ

36.

Проверить значимость уравнения регрессии –
установить:
соответствует ли модель исходным данным и
достаточно ли включенных в уравнение
объясняющих переменных.
Проверка значимости уравнения регрессии
происходит на основе дисперсионного анализа.

37.

Основное положение дисперсионного анализа
2
2
2
ˆ
ˆ
(
y
y
)
(
y
y
)
(
y
y
)
i
i
i
, или
i
Qобщ
=
Qфакт
+
Qост

38.

СХЕМА ДИСПЕРСИОННОГО АНАЛИЗА
(n – число наблюдений, k –число объясняющих переменных).
Дисперсия
Число
Компоненты
Сумма квадратов степеней на одну степень
дисперсии
свободы
свободы
Общая
Qобщ ( yi y)
2
Факторная
Qфакт ( yˆi y ) 2
(объясненная
регрессией)
Остаточная
Qост ( yi yˆi ) 2
n 1
k
n–k–1
S
S
S
2
общ
2
факт
2
ост
Qобщ
Qфакт
n 1
k
Qост
n k 1

39.

Выдвигают гипотезу о не значимости уравнения в
целом, которая формально сводится к гипотезе о равенстве
нулю параметров регрессии:
H 0 : 1 0 .
Альтернативная ей гипотеза о значимости уравнения –
гипотеза о неравенстве нулю параметров регрессии:
H1 : 1 0 .
Значимость уравнения проверяют с помощью F–
критерия Фишера:
2
S регр
Qрегр / k
Qрегр (n 2)
Fнабл 2
, где
Sост Qост /(n k 1)
Qост
n – число выборочных наблюдений, k – число
объясняющих переменных.
Если Fнабл>Fкр( ; ν1=k=1, ν2=n–2), то гипотеза
отвергается и уравнение считается значимым.

40.

R2 также применяется для проверки значимости
уравнения регрессии.
R 0.
2
R
0.
Н1:
Н0:
2
Для этого рассчитывают статистику:
2
R
F
(n 2) .
2
1 R
Если Fнабл>Fкр, то гипотеза отвергается и уравнение
считается значимым.

41.

ПРОВЕРКА ЗНАЧИМОСТИ
КОЭФФИЦИЕНТОВ
УРАВНЕНИЯ РЕГРЕССИИ

42.

Коэффициент называется значимым, если есть
достаточно высокая вероятность того, что его истинное
значение отлично от нуля.
H0: βj=0.
Для проверки гипотезы рассчитывают:
tнабл j
bj
Sˆb , где
j
Sˆb
0
Sˆ 2 хi2
n
n xi2 ( xi ) 2
i 1
Sˆb
1
Sˆ 2
xi
2
S
n Sx
n
S
n
2
n Sx .
( xi x )
i 1

43.

Если использовать матричную форму записи, то:
2
2
T
1
ˆ
ˆ
Sb j S [( X X ) ] jj
–
дисперсия
коэффициента
регрессии bj;
2
ˆ
S
– несмещенная оценка остаточной дисперсии;
T
1
[( X X ) ] jj
– элементы обратной матрицы, стоящие на
главной диагонали;
Sˆb j – стандартная ошибка коэффициента bj.
Если |tнабл|>tкр(α; ν=n–2), то гипотеза H0 отвергается и
коэффициент считается значимым.
Если |tнабл| tкр, то гипотеза H0 не отвергается.

44.

ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ
КОЭФФИЦИЕНТОВ РЕГРЕССИИ

45.

Доверительным интервалом называется интервал,
относительно которого можно с заранее выбранной
вероятностью утверждать, что он содержит значения
прогнозируемого показателя.
Интервальная оценка для параметра β0:
0 b0 t ,n 2 Sˆb0
, где
tкр(α; ν=n–2) определяется из таблицы распределения
Стьюдента для двусторонней критической области для
уровня значимости α и числа степеней свободы ν=n–2.
Аналогично определяется интервальная оценка для
коэффициента β1:
1 b1 t ,n 2 Sˆb1
1.

46.

ПРОГНОЗИРОВАНИЕ С
ПРИМЕНЕНИЕМ УРАВНЕНИЯ
РЕГРЕССИИ

47.

Регрессионные модели могут быть использованы для
прогнозирования результативной переменной Y:
yˆ пр b0 b1 xпр .
Данный прогноз называется точечным.
Интервальная оценка для уравнения регрессии yˆ в
точке, определяемой начальным условием X=xпр
находится следующим образом:
2
1 ( xпр x )
ˆ
yпр yˆ пр t ,n 2 S 1 n
n
2 .
( xi x )
i 1

48.

Доверительный интервал имеет наименьшую величину,
когда xnp x , а по мере удаления x0 от x ширина
доверительного интервала
оценки yˆ снижается.
увеличивается,
и
точность