Similar presentations:
Свойства поверхностного интеграла второго рода
1.
Свойства поверхностного интеграла второго рода.1. Pdydz Qdxdz Rdxdy Pdydz Qdxdz Rdxdy ,
где через и обозначена одна и та же поверхность , но с двумя
противоположными ориентациями.
2. C Pdydz Qdxdz Rdxdy C Pdydz Qdxdz Rdxdy ,
C const .
3. Интеграл от суммы функций равен сумме интегралов от
соответствующих слагаемых.
4. Pdydz Qdxdz Rdxdy
Pdydz Qdxdz Rdxdy Pdydz Qdxdz Rdxdy ,
1
2
где 1 2 и поверхности 1 и 2 пересекаются лишь по границе
их разделяющей.
2.
5. Если 1 , 2 , 3 – цилиндрические поверхности собразующими параллельными соответственно осям OX, OY и OZ, то
P x, y, z dydz Q x, y, z dxdz R x, y, z dxdy 0 .
1
2
3
§ 13. Вычисление поверхностного интеграла второго рода
Пусть функция R x, y, z непрерывна в точках поверхности ,
заданной уравнением z z x, y , где z x, y – непрерывная функция в
замкнутой области Dxy – проекции поверхности на координатную
плоскость OXY. В этом случае
R x, y, z dxdy R x, y, z x, y dxdy ,
Dxy
где знак «плюс» соответствует стороне поверхности, для которой угол
между нормалью n к поверхности и осью OZ – острый; знак
«минус» соответствует стороне поверхности, для которой угол –
тупой.
3.
Если поверхность задана уравнением y y x, z , Dxz – замкнутаяобласть, являющаяся проекцией поверхности S на координатную
плоскость OXZ, то
Q x, y, z dxdz Q x, y x, z , z dxdz ,
Dxz
где знак «плюс» соответствует стороне поверхности, для которой угол
между нормалью n к поверхности и осью OY – острый; знак
«минус» соответствует стороне поверхности, для которой угол –
тупой.
Если поверхность задана уравнением x x y, z , Dyz – замкнутая
область, являющаяся проекцией поверхности S на координатную
плоскость OYZ, то
P x, y, z dydz P x y, z , y, z dydz ,
D yz
где знак «плюс» соответствует стороне поверхности, для которой угол
между нормалью n к поверхности и осью OX – острый; знак
«минус» соответствует стороне поверхности, для которой угол –
тупой.
4.
В общем случае поверхность проектируется на всекоординатные плоскости. В этом случае имеем
P x, y, z dydz Q x, y, z dxdz R x, y, z dxdy
P x y, z , y, z dydz Q x, y x, z , z dxdz R x, y, z x, y dxdy .
D yz
Dxz
Dxy
Поверхностные интегралы первого и второго рода связаны
соотношением
Pdydz Qdxdz Rdxdy P cos Q cos R cos ds ,
где cos , cos , cos – направляющие косинусы нормали n к
выбранной стороне поверхности , и справедливы соотношения
dxdy ds cos , dxdz ds cos , dydz ds cos ,
где ds – элемент площади поверхности .
5.
Пример. Вычислить xdydz zdxdz 2dxdy по верхней сторонечасти плоскости x y z 1, лежащей в первом октанте.
Решение. В данном случае P x , Q z , R 1 , нормаль n
образует с осями координат одинаковые острые углы (рис.
1.12). Положим n 1; 1; 1 , тогда получим
1
cos cos cos
0 . Следовательно,
3
Pdydz Qdxdz Rdxdy
n 12 12 12 3 ,
Z
1 C
x+z=1
1 y z dydz zdxdz 2 dxdy
D yz
1
Dxz
1 y
O
Dxy
1
1 x
1
dy 1 y z dz dx zdz 2
2
0
0
0
0
y+z=1
n
A 1
B1 Y
x+y=1
X
Рисунок 1.12
6.
1 y1 x
1
1
2
2
z
z
1 y
1 x
dy 1 y z dx 1
dy
dx 1
2
2
2
2 0
0
0
0
0
0
1
2
1
2
y 1
3 1
3 2
0
x 1
3 1
1 4
1 1 .
3 2 0
3 3
Пример. Объем тела, ограниченного снизу поверхностью 1
( z z1 x, y ), сверху поверхностью 2 ( z z 2 x, y ), сбоку
цилиндрической поверхностью с образующей параллельной оси OZ,
равен
V z 2 x, y dxdy z1 x, y dxdy
2
z 2 z1 dxdy.
1
1
7.
§ 14. Формула Остроградского-ГауссаТеорема. Если функции P x, y, z , Q x, y, z , R x, y, z
непрерывны вместе со своими частными производными первого
порядка в пространственной области , то справедлива формула
Остроградского-Гаусса
P Q R
x y z dxdydz Pdydz Qdxdz Rdxdy ,
– граница области , интегрирование производится по внешней
стороне границы области.
Формула Остроградского-Гаусса связывает между собой
поверхностный интеграл второго рода по замкнутой поверхности и
тройной интеграл по объему, ограниченному этой поверхностью.
Пример. Вычислить xdydz zdzdx 2dxdy , где поверхность
– внешняя сторона пирамиды OABC, ограниченной плоскостями
x y z 1, x 0 , y 0 , z 0 (рис. 1.12).
8.
Решение. Используя формулу Остроградского-Гаусса,учитывая, что P x , Q z , R 2 , получим
P Q R
dxdydz
I Pdydz Qdxdz Rdxdy
x y z
и
1
1 0 0 dxdydz Vпир .
6
Используя
этот
результат,
можно
иначе
вычислить
xdydz zdzdx 2dxdy по верхней стороне части плоскости
x y z 1, лежащей в первом октанте. Действительно, обозначим
I .
ABC OAB OAC OBC
9.
IТогда получим
ABC
OAB OAC OBC
1
1 x
1
1
1
2 dxdy zdxdz 0 dydz 2 dx zdz
6
6
2 0 0
OAB
OAC
OBC
2 1 x
z
7
7
1 x
7 1 x
7 1 4
dx
dx
.
6 0 2 0
6 0 2
6 3 2 0 6 6 3
1
1
2
3 1








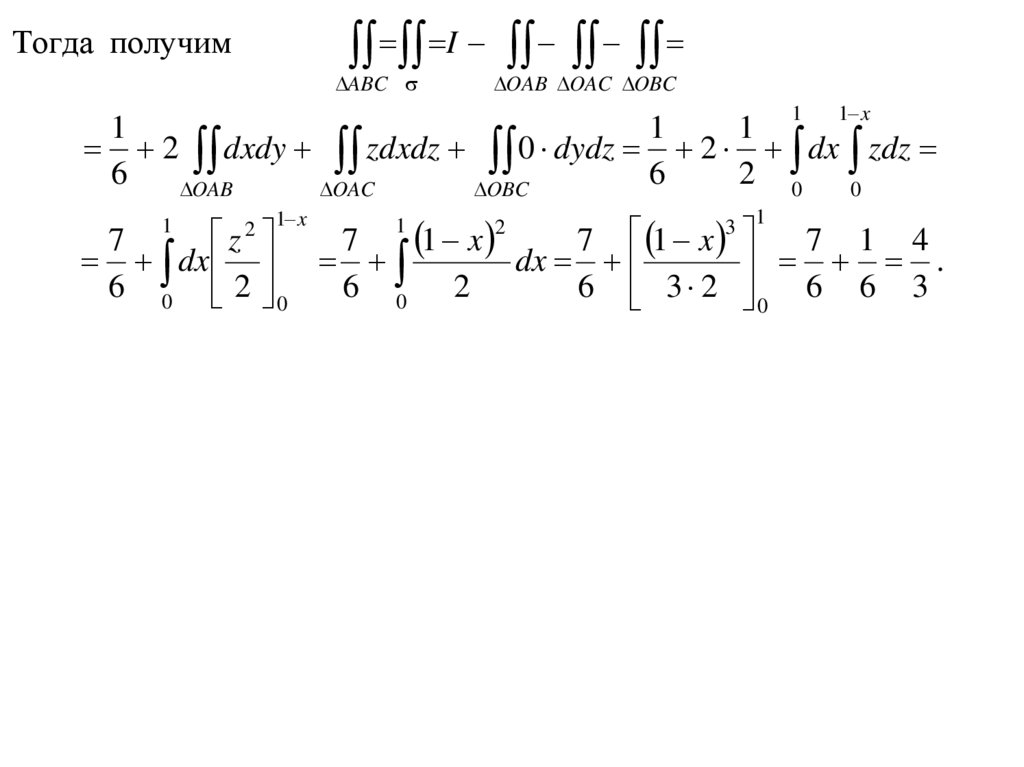
 mathematics
mathematics








