Операции над множествами Лекция № 3

1.

Раздел 1. Элементы теории множеств
Тема 1.2. Операции над множествами
Операции над множествами
Лекция № 3

2. Понятие булеана

Множество всех подмножеств заданного множества называется
БУЛЕАНОМ. Булеан множества A будем обозначать (A).
Если мощность заданного множества равна n, то число
элементов в булеане будет 2n, т.е. | (A) | = 2n.
Разберем, как выглядит булеан для некоторых множеств.
Пусть задано множество A = {1, 2}. Тогда булеан этого
множества будет иметь вид:
(A) = { , {1}, {2}, {1, 2}}.
Пусть задано множество B = {a, b, c}. Тогда булеан этого множества будет
иметь вид:
(B) = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}.

3. Равенство множеств

Два множества А и В называются РАВНЫМИ ( А = В ), если они
состоят из одних и тех же элементов, то есть каждый элемент
множества А является элементом множества В и наоборот,
каждый элемент множества В является элементом множества А .
Например, множества A = {к, л, о, у, н} и B ={к, у, л, о, н} будут
равными.
Также множества M = {к, о, л} и P = {к, о, л, о, к, о, л} тоже будут
равными. Кроме того, множество P нужно записать в виде
P = {к, о, л}, убрав повторяющиеся элементы в множестве.
В этом случае пишут, что A = B, M = P.

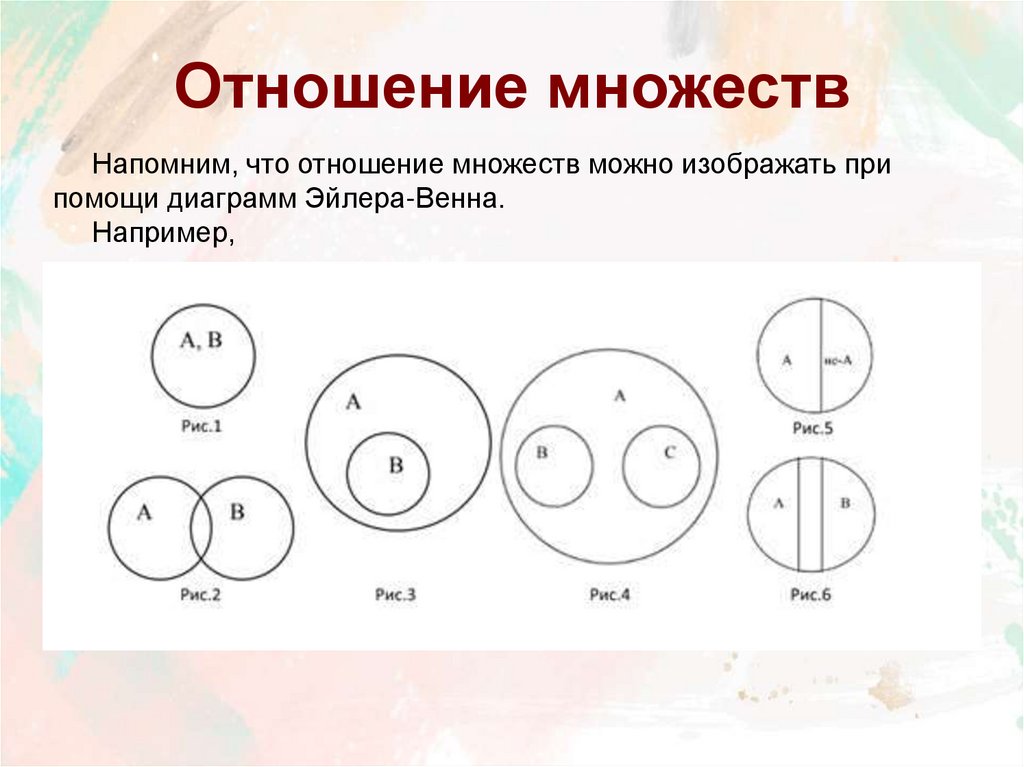
4. Отношение множеств

Напомним, что отношение множеств можно изображать при
помощи диаграмм Эйлера-Венна.
Например,

5. Операции над множествами

К операциям над множествами относятся следующие операции:
1) Объединение множеств
2) Пересечение множеств
3) Разность множеств
4) Симметрическая разность множеств
5) Дополнение множества
На диаграммах Эйлера-Венна результат выполнения всех
перечисленных операций обозначается штриховкой.
Рассмотрим каждую из перечисленных операций подробнее.

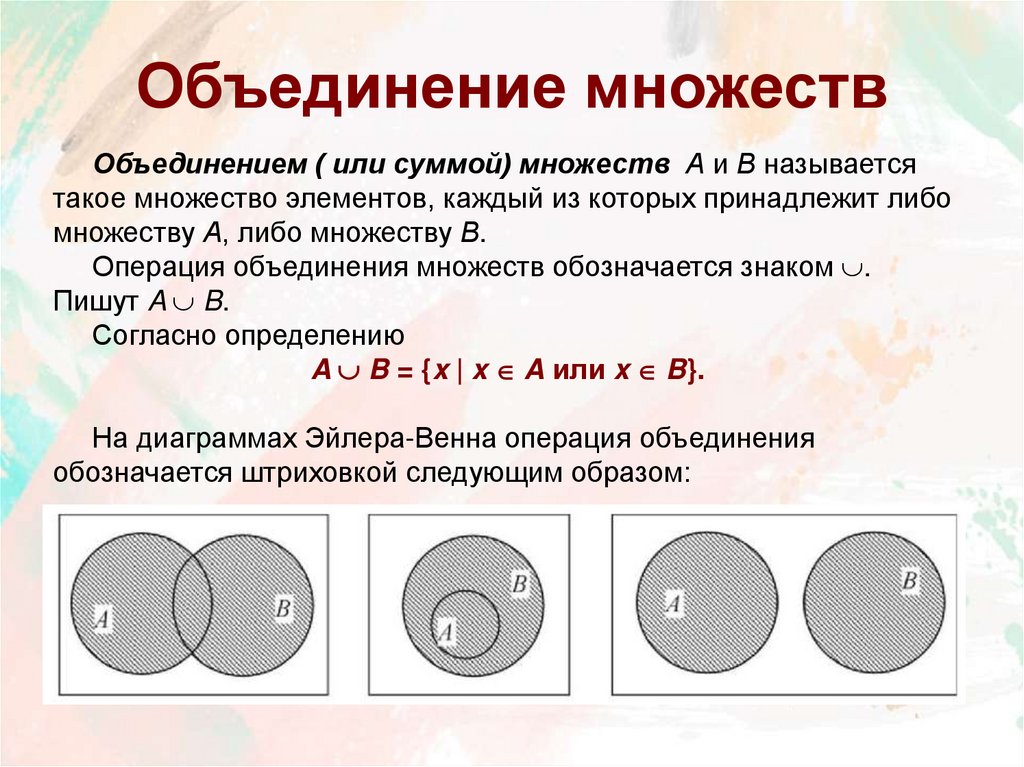
6. Объединение множеств

Объединением ( или суммой) множеств А и В называется
такое множество элементов, каждый из которых принадлежит либо
множеству А, либо множеству В.
Операция объединения множеств обозначается знаком .
Пишут A B.
Согласно определению
A B = {x | x A или x B}.
На диаграммах Эйлера-Венна операция объединения
обозначается штриховкой следующим образом:

7. Объединение множеств

Пусть заданы множества А = {1, 2, 4} и B = {3, 4, 5, 6}. Тогда в
результате выполнения операции объединения получим
A B = {1, 2, 3, 4, 5, 6}
На диаграмме Эйлера-Венна результат выполнения операции
будет показан следующей штриховкой:
B
A
3
2
4
1
6
5

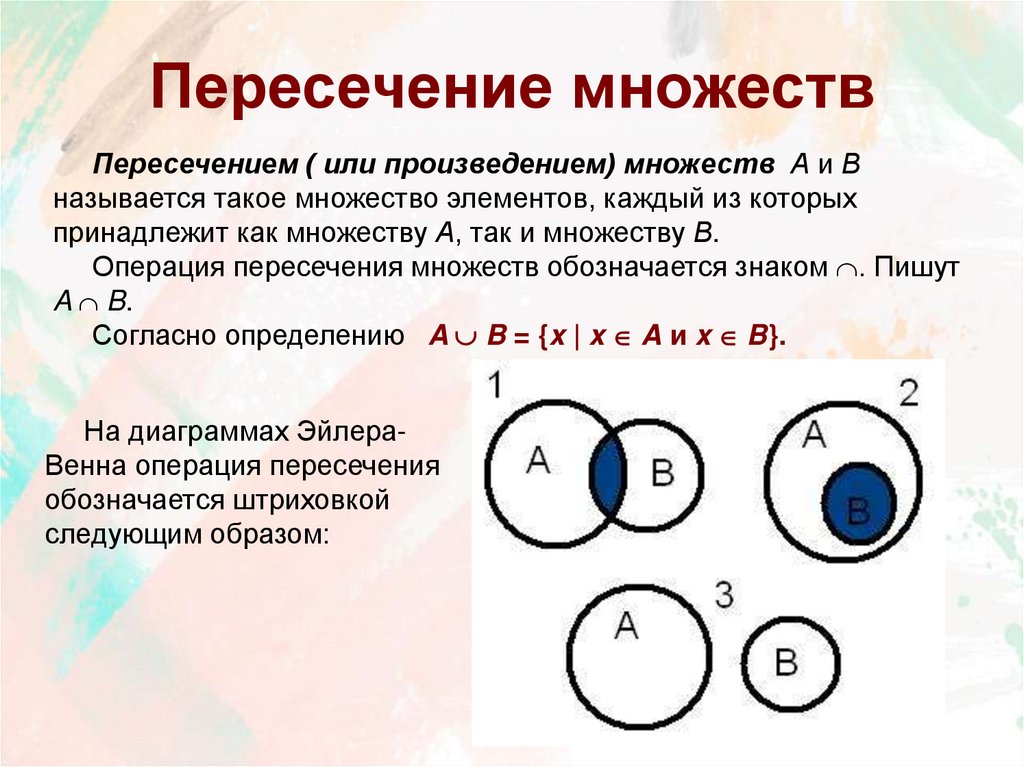
8. Пересечение множеств

Пересечением ( или произведением) множеств А и В
называется такое множество элементов, каждый из которых
принадлежит как множеству А, так и множеству В.
Операция пересечения множеств обозначается знаком . Пишут
A B.
Согласно определению A B = {x | x A и x B}.
На диаграммах ЭйлераВенна операция пересечения
обозначается штриховкой
следующим образом:

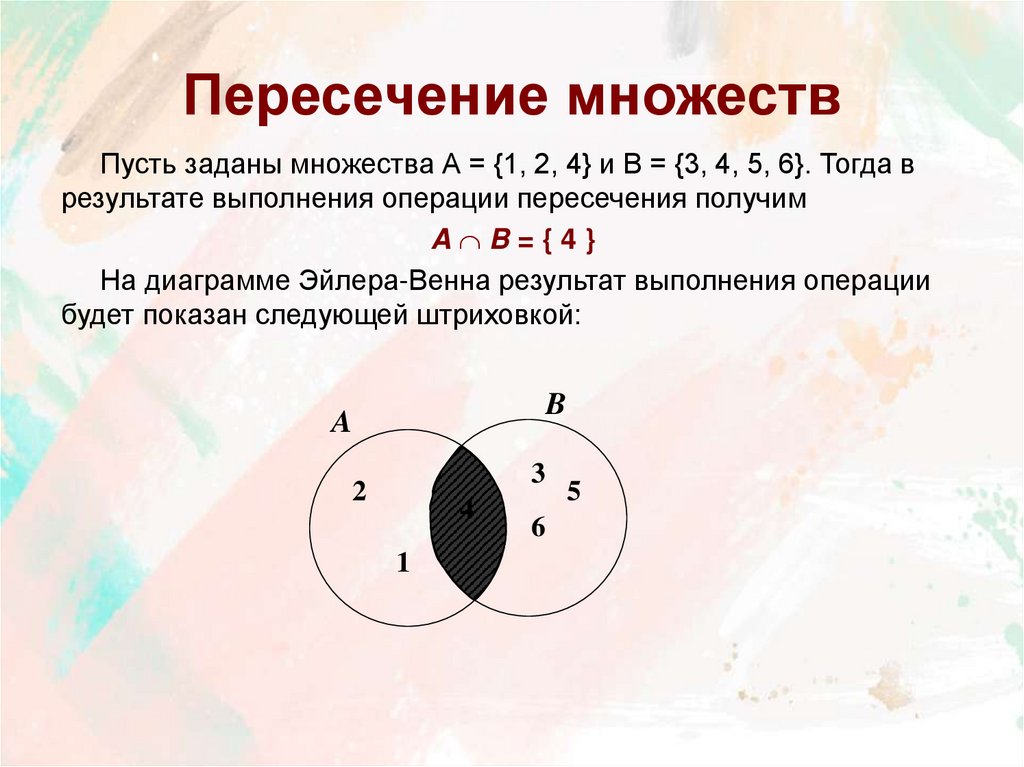
9. Пересечение множеств

Пусть заданы множества А = {1, 2, 4} и B = {3, 4, 5, 6}. Тогда в
результате выполнения операции пересечения получим
A B={4}
На диаграмме Эйлера-Венна результат выполнения операции
будет показан следующей штриховкой:
B
A
3
2
4
1
6
5

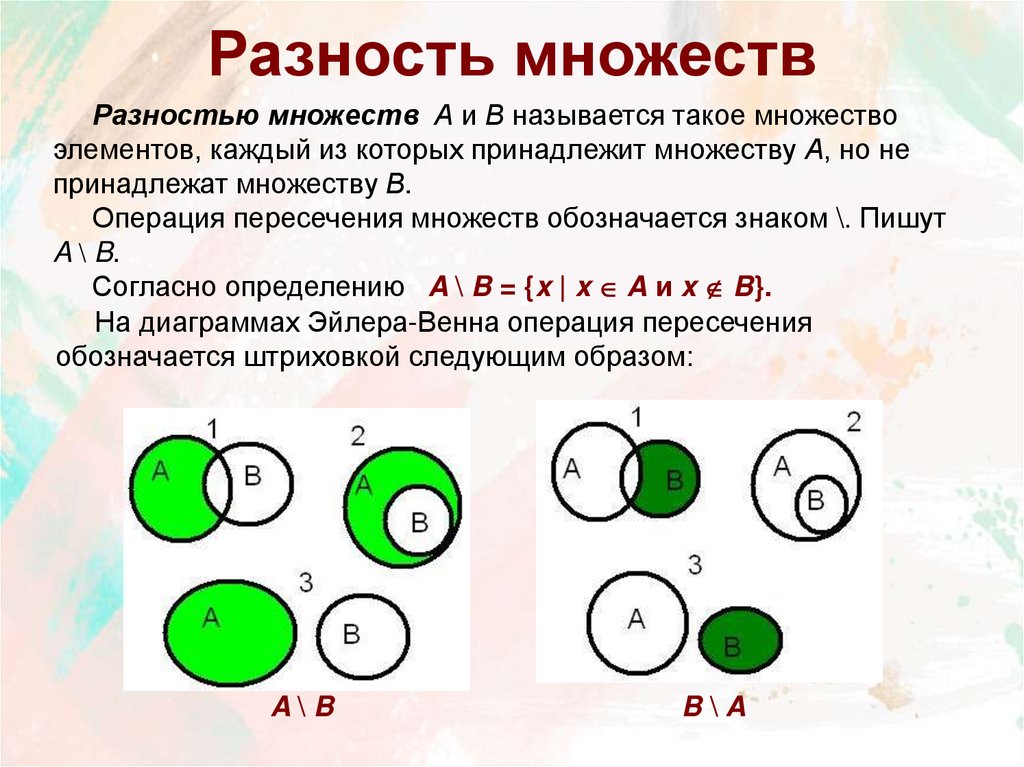
10. Разность множеств

Разностью множеств А и В называется такое множество
элементов, каждый из которых принадлежит множеству А, но не
принадлежат множеству В.
Операция пересечения множеств обозначается знаком \. Пишут
A \ B.
Согласно определению A \ B = {x | x A и x B}.
На диаграммах Эйлера-Венна операция пересечения
обозначается штриховкой следующим образом:
A\B
B\A

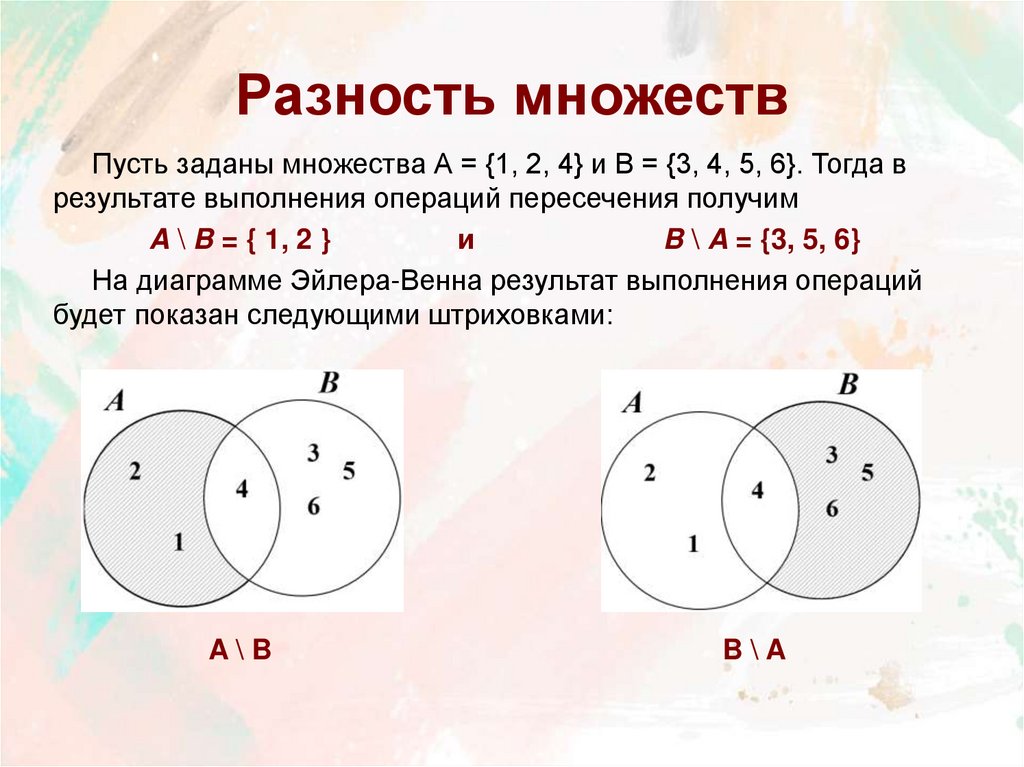
11. Разность множеств

Пусть заданы множества А = {1, 2, 4} и B = {3, 4, 5, 6}. Тогда в
результате выполнения операций пересечения получим
A \ B = { 1, 2 }
и
B \ A = {3, 5, 6}
На диаграмме Эйлера-Венна результат выполнения операций
будет показан следующими штриховками:
A\B
B\A

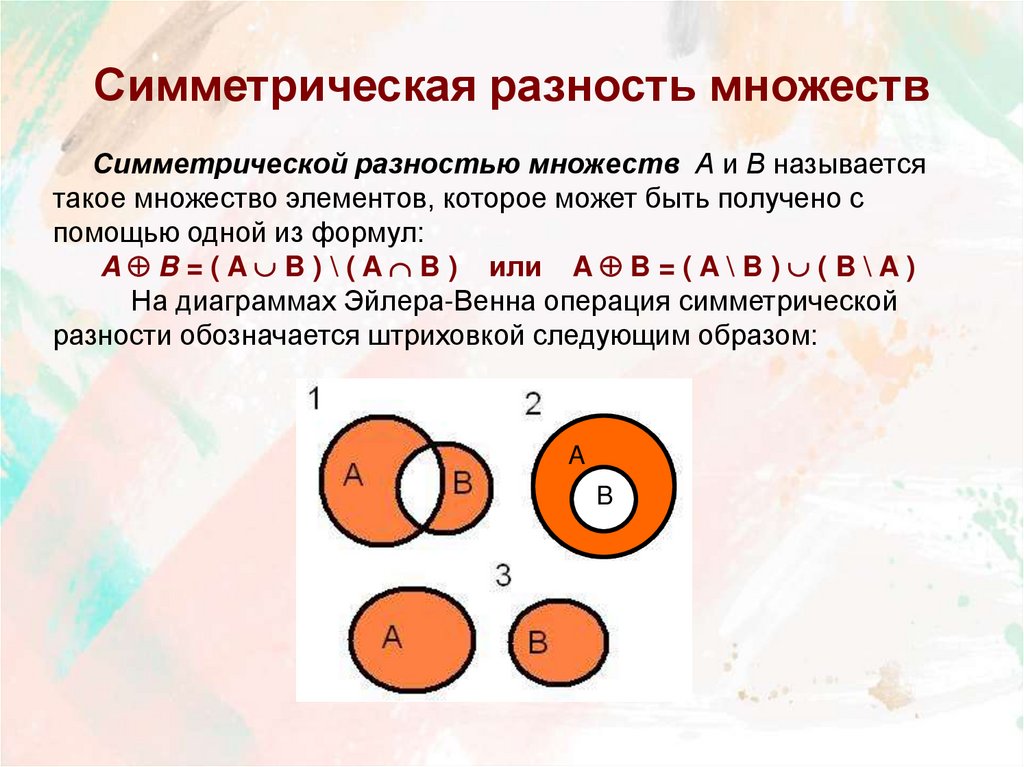
12. Симметрическая разность множеств

Симметрической разностью множеств А и В называется
такое множество элементов, которое может быть получено с
помощью одной из формул:
A B = ( A B ) \ ( A B ) или A B = ( A \ B ) ( B \ A )
На диаграммах Эйлера-Венна операция симметрической
разности обозначается штриховкой следующим образом:
A
B

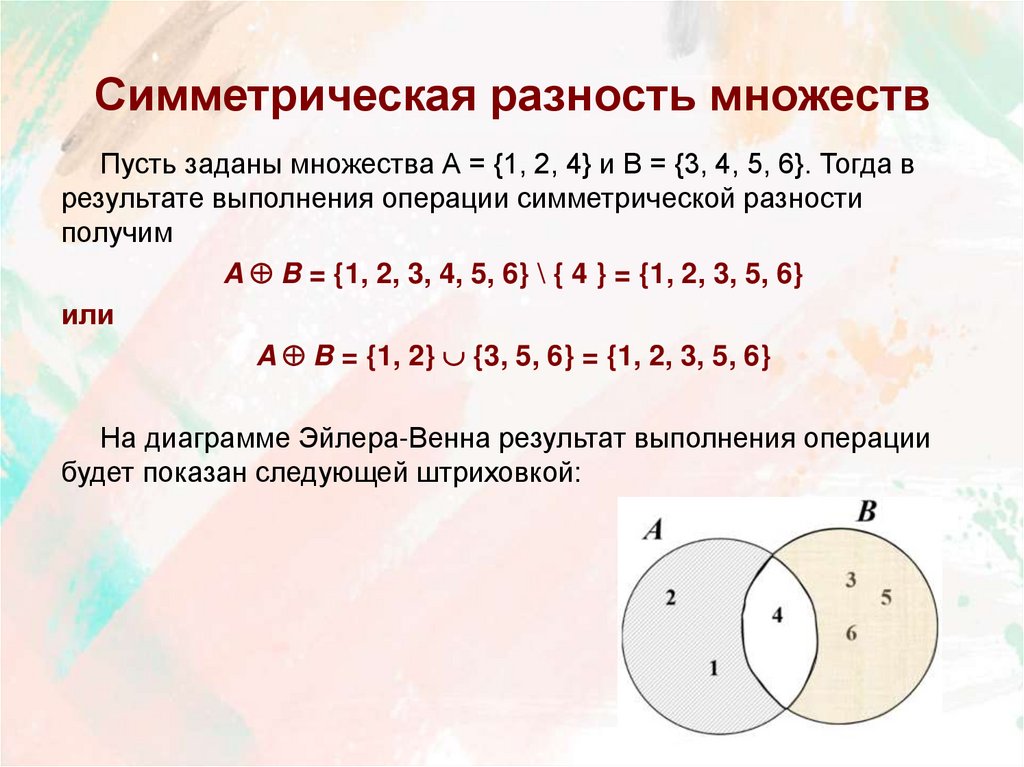
13. Симметрическая разность множеств

Пусть заданы множества А = {1, 2, 4} и B = {3, 4, 5, 6}. Тогда в
результате выполнения операции симметрической разности
получим
A B = {1, 2, 3, 4, 5, 6} \ { 4 } = {1, 2, 3, 5, 6}
или
A B = {1, 2} {3, 5, 6} = {1, 2, 3, 5, 6}
На диаграмме Эйлера-Венна результат выполнения операции
будет показан следующей штриховкой:

14. Дополнение множества

Дополнением множества А называется множество всех
элементов, не принадлежащих множеству A, т.е. множество U \ A,
где U – универсальное множество: A U \ A
На диаграммах Эйлера-Венна дополнение множества
обозначается штриховкой следующим образом:

15. Выполнить самостоятельно:

Для заданных множеств А = {1, 2, 6},
C = {4, 5, 7} найти:
1) A B
2) B \ C
3) B C
4) A C
5) A B
6) (A)
B = {2, 3, 4, 7, 8} и