Волны. Тема 5

1.

Тема 5 ВОЛНЫ
5.1. Распространение волн в упругой среде
5.2. Уравнение плоской и сферической волны
5.3. Волновое уравнение
5.4. Электромагнитные волны
5.5. Энергия и импульс электромагнитных волн
СРС

2.

5.1. Распространение волн в упругой среде
Колеблющиеся тело, помещенное в упругую среду,
является источником колебаний, распространяющихся от него во
все стороны.
Круговая волна на поверхности
жидкости, возбуждаемая точечным
источником
Генерация акустической волны
громкоговорителем.
Процесс распространения колебаний в пространстве
называется волной.

3.

При распространении волны, частицы среды не движутся вместе с
волной, а колеблются около своих положений равновесия.
Вместе с волной от частицы к частице, передается лишь состояние
колебательного движения и его энергия. Поэтому основным свойством
всех волн независимо от их природы является перенос энергии без
переноса вещества.

4.

Волны бывают поперечными (колебания происходят в
плоскости, перпендикулярной направлению распространения), и
продольными (сгущение и разряжение частиц среды происходят в
направлении распространения).
В поперечной волне колебания
происходят в направлении,
перпендикулярном направлению
распространения волны
Процесс распространения
продольной упругой волны

5.

Если взаимосвязь между частицами среды
осуществляется силами упругости, возникающими
вследствие деформации среды при передаче
колебаний от одних частиц к другим, то волны
называются упругими (звуковые, ультразвуковые,
сейсмические и др. волны).
Упругие поперечные волны возникают в среде,
обладающей сопротивлением сдвигу,
вследствие этого:
• в жидкой и газообразной средах возможно
возникновение только продольных волн;
• в твердой среде возможно возникновение как
продольных, так и поперечных волн.

6.

Наложение продольной и поперечной волн равной
амплитуды, сдвинутых по фазе на π/2.
В результате каждая масса совершает круговые движения.

7.

Волна на поверхности жидкости - суперпозиция
продольного и поперечного движения молекул

8.

Движение молекул в волне на поверхности жидкости
У поверхностных волн взаимосвязь между соседними
молекулами при передаче колебаний осуществляется не силами
упругости, а силами поверхностного натяжения и тяжести. В
случае малой амплитуды волны каждая молекула движется по
окружности, радиус которой убывает с расстоянием от
поверхности. Нижние молекулы находятся в покое

9.

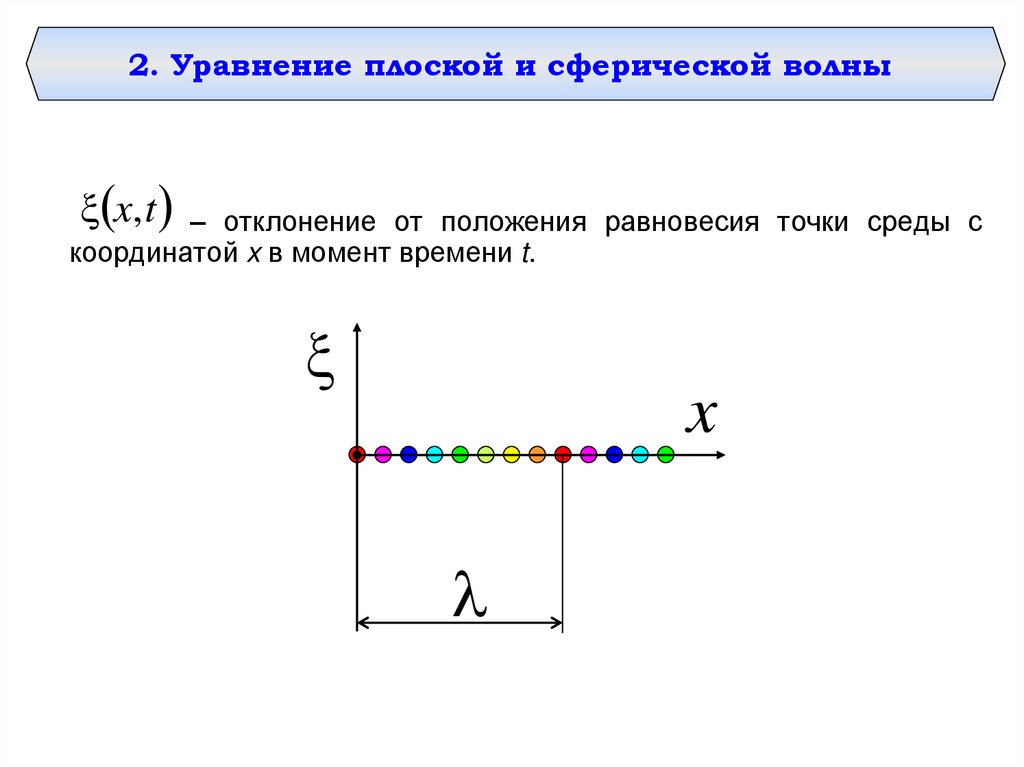
2. Уравнение плоской и сферической волны
x, t – отклонение от положения равновесия точки среды с
координатой x в момент времени t.
x

10.

Волновая функция
ξ ξ( x, y, z, t )
Расстояние между ближайшими частицами, колеблющимися в
одинаковой фазе, называется длиной волны :
λ υT
– частота
1
T
ν
– период
υ λν υ – скорость распространения волны :
В среде без дисперсии скорость распространения волны
есть фазовая скорость, или скорость распространения
поверхности постоянной фазы.

11.

Фронт волны – геометрическое место точек, до
которых доходит возмущение в момент времени t: это
та поверхность, которая отделяет часть пространства, уже
вовлеченную в волновой процесс, от области, в которой
колебаний еще не возникли.
(В однородной среде
направление распространения перпендикулярно фронту
волны )
Волновая поверхность –
геометрическое место точек,
колеблющихся в одинаковой фазе.
Число волновых поверхностей –
бесконечно.
Фронт волны – один.
Волновые поверхности неподвижны,
Фронт волны все время
перемещается

12.

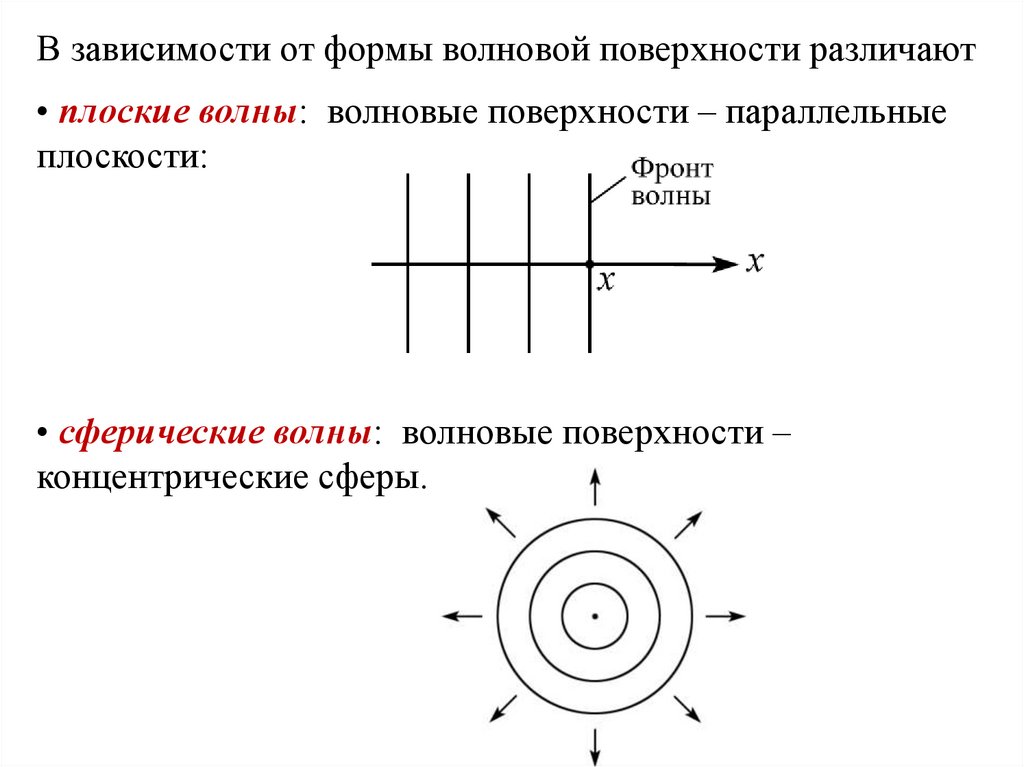
В зависимости от формы волновой поверхности различают
• плоские волны: волновые поверхности – параллельные
плоскости:
• сферические волны: волновые поверхности –
концентрические сферы.

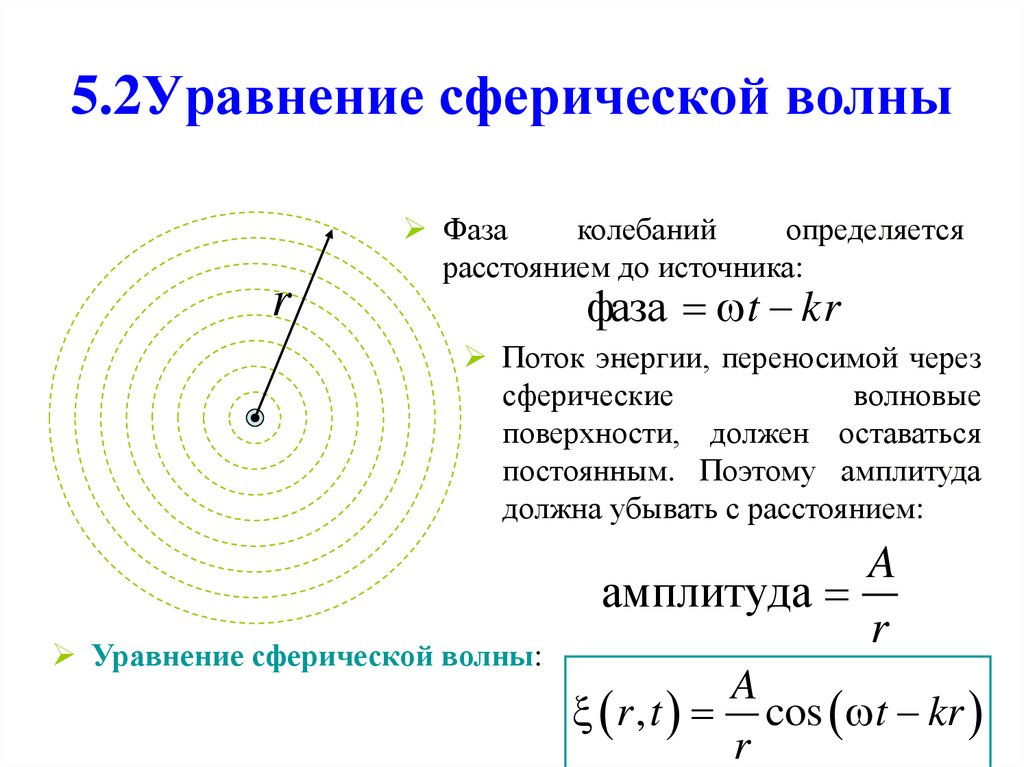
13. 5.2Уравнение сферической волны

r
Фаза
колебаний
определяется
расстоянием до источника:
фаза t kr
Поток энергии, переносимой через
сферические
волновые
поверхности, должен оставаться
постоянным. Поэтому амплитуда
должна убывать с расстоянием:
Уравнение сферической волны:
A
амплитуда
r
A
r , t cos t kr
r

14. 5.2 Уравнение плоской волны

X
x
Источник колебаний находится в начале координат: 0, t А cos t
Колебания в точке с координатой x запаздывают на время:
x
x, t A cos t A cos t x
V
V
x
V

15. Уравнение плоской волны

2
2
x, t A cos t
x A cos t
x
Волновое число:
2
k
V
k
Уравнение плоской волны:
x, t A cos t kx
Волна, бегущая справа налево:
x, t А cos t kx

16. Плоская волна в пространстве

r , t A cos t kl
l r cos n r cos n r
2
k k n
n
' Волновой вектор:
x
0, t A cos t
y
r
равен по величине волновому числу
n
x
направлен
вдоль
направления
распространения волны
r , t A cos t kr
l
x, y, z, t A cos t k x x k y y k z z

17.

5.3. Волновое уравнение
Распространение волн в однородной среде в общем случае
описывается волновым уравнением – дифференциальным
уравнением в частных производных:
ξ ξ ξ 1 ξ
2 2 2 2
2
x
y
z
υ t
2
2
2
2
1 ξ
ξ 2 2
υ t
2
или
2
Всякая функция, удовлетворяющая этому
уравнению,
описывает некоторую волну, причем υ - фазовая скорость
волны

18.

Решением волнового уравнения
1 ξ
ξ 2 2
υ t
2
2
является уравнение любой волны, например
сферической:
или плоской :
A
ξ cos(ωt kr )
r
ξ A cos(ωt kr )
ξ 1 ξ
x 2 υ2 t 2
2
2
Для плоской волны, распространяющейся вдоль оси x,
2
2
2
волновое уравнение упрощается:
2
Напоминаю, что =оператор Лапласа: x
2
y
2
z
2

19.

5.4. Электромагнитные волны
Возможность существования
электромагнитных волн предсказывал еще
Майкл Фарадей в 1832 г., обобщая
известные к тому времени данные по
изучению электричества и магнетизма.
Теоретически обосновал это
предположение Дж. Максвелл.

20.

Максвелл Джеймс Клерк
(1831 – 1879) – английский
физик,
член
Эдинбургского
(1855) и Лондонского (1861)
королевских обществ с 1871 г.
Работы
посвящены
электродинамике, молекулярной
физике,
общей
статистике,
оптике,
механике,
теории
упругости.
Самым большим научным достижением Максвелла
является созданная им в 1860 – 1865 теория
электромагнитного поля, которую он сформулировал в
виде системы нескольких уравнений (уравнения
Максвелла), выражающих все основные закономерности
электромагнитных явлений.

21.

Полная система уравнений Максвелла в
дифференциальной и интегральной формах имеет вид:
divD ,
S D, dS V dV
B
B
rotE
,
L E, d l S t dS
t
div B 0,
B, dS 0
S
D
L H, d l S j t dS
B μ 0μH,
D
rotH j
,
t
D ε 0εE

22.

Изменяющееся во времени поле B( t ) порождает вихревое
переменное электрическое поле E(. t )
А изменяющееся во времени поле D 0 E( t )
переменное вихревое магнитное поле H( t ) .
порождает
Из этого следует возможность существования переменных
электромагнитных полей вдали от зарядов и токов
проводимости не только в среде, но и в вакууме ( 1, 1).
Электрические и магнитные переменные поля взаимно
порождают друг друга, удаляясь от источника и теряя
связь с ним. Возникает электромагнитная волна, которая
существует в пространстве даже после выключения
источника.
Источниками
электромагнитных
волн
являются: движущиеся с ускорением электрические заряды,
переменные токи и изменяющиеся во времени электрические
и магнитные поля.

23.

Таким образом, существование электромагнитного поля следует из
уравнений Максвелла.
Упрощая задачу, будем считать, что среда:
однородная и изотропная const , const (свойства не зависят от
направления),
нейтральная, т.е. отсутствуют заряды ( 0 ),
непроводящая, т.е. отсутствуют токи
( j 0 ).
Для рассматриваемых свойств среды эти уравнения имеют вид:
div E 0 ,
rot E 0
H
,
t
div H 0 ,
rot H 0
E
t

24.

Волновое уравнение
Любые волновые процессы должны описываться волновым
уравнением, которое связывает вторые производные по времени и
координатам.
Используя полученную систему и известное тождество векторной
алгебры
a , b , c b a , c c a , b
H
rot E 0
,
, найдем ротор от обеих частей уравнения
t
2
H
E
rot
rotE
rot
rotH
0 t t
o o
2
t
rot rotE , , E , E , E grad divE , E , E
Учтем, что
2
2
2
, 2 2 2 2
x
y
z

25.

Волновые уравнения
E
2
E 0 0 2
t
2
Эти соотношения представляют
уравнения для полей E и H .
Вспомним, что в волновом уравнении
H
H 0 0 2
t
2
2
собой
идентичные
1 2
2 2
v t
2
волновые
множитель
перед второй производной в правой части – это величина, обратная
квадрату фазовой скорости волны.
1
0 0 2
v

26.

2
E
2 E 0 0 2
t
1
Следовательно, 0 0 2
v
Оказалось, что в вакууме эта скорость для
2
электромагнитной волны равна скорости света.
H
2
H 0 0 2
1
0 0 2
t
c
Тогда волновые уравнения для полей E и H можно записать как
1 H
2
H 2
с t 2
2
1 E
2
E 2 2
с t
2
Эти уравнения указывают на то, что электромагнитные поля могут
существовать в виде электромагнитных волн, фазовая скорость
которых в вакууме равна скорости света.

27.

Скорость распространения электромагнитных волн в среде зависит
от ее электрической и магнитной проницаемостей.
n εμ - абсолютный показатель преломления.
1
υ
μ 0ε 0
1
c
με n
и
c
n
υ
Следовательно, показатель преломления
есть физическая величина, равная отношению
скорости электромагнитных волн в вакууме к их
скорости в среде.

28.

Герц Генрих Рудольф (1857 – 1894) – немецкий
физик. Окончил Берлинский университет (1880 г.) и
был ассистентом у Г. Гельмгольца. В 1885 – 89 гг. –
профессор Высшей технической школы в Карлсруэ.
Основные работы относятся к электродинамике,
одним из основоположников которой он является,
и механике.
В 1888г. экспериментально доказал существование
электромагнитных
волн,
распространяющихся
в
свободном
пространстве,
предсказанных
теорией
Максвелла. Экспериментируя с электромагнитными
волнами, наблюдал их отражение, преломление,
интерференцию, поляризацию. Установил, что скорость
распространения электромагнитных волн равна скорости
света. В 1887 наблюдал внешний фотоэффект.
Исследования Герца посвящены также катодным лучам,
теории удара упругих тел и т. п.

29.

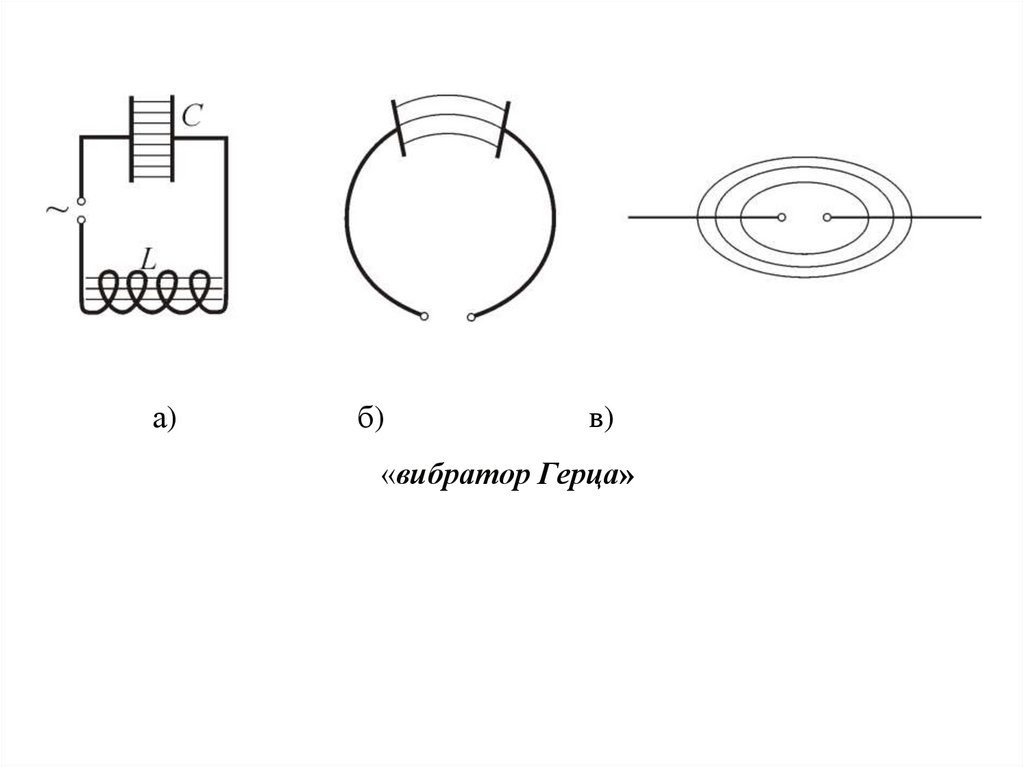
3. Экспериментальное исследование ЭМВ
В колебательном контуре, образованном конденсатором С и
катушкой L электрическое поле сосредоточено в зазоре между
обкладками, а магнитное – внутри катушки.
В окружающем конденсатор и катушку пространстве поля
практически равны нулю.

30.

а)
б)
в)
«вибратор Герца»

31.

В ходе своих исследований Герц
https://viol.uz/kak-vse-nachinalos/
обнаружил, что если расстояние между вибратором и
приемником (резонатором) меньше одного метра, то поле
вибратора в этой области соответствует излучению поля диполем и
убывает обратно пропорционально кубу расстояния (эту зону
r λ
назвали ближней зоной, здесь

32.

Однако на расстояниях более трех метров поле
убывает значительно медленнее (это волновая зона r λ)
и неодинаково в различных направлениях.
В направлении оси вибратора поле практически
исчезает на расстоянии четырех метров, а в
направлении, перпендикулярном к оси вибратора,
достигает расстояния двенадцати метров и более.

33. При подготовке к лабораторным работам по оптике Обязательно законспектировать!!!!

• Основные положения теории оптических
явлений.
………………….
• Глава 1.
Электромагнитные волны.
• …………………….
5. Свойства волн.

34.

1. В любой точке векторы напряженности электрического
и магнитного полей взаимно перпендикулярны
и
перпендикулярны направлению распространения υ , т.е.
образуют правовинтовую систему: E Η υ
2. Колебания
электромагнитных полей
происходят поперек
направлению
распространения волны.
В однородной, изотропной
среде волна поперечна
для полей E и Η
3. Электрическое и магнитное поля находятся в фазе,
т.е. они достигают максимума и обращаются в нуль в
одних и тех же точках. 0 E 0 H
E vB ,

35.

ЭМВ представляют собой поперечные волны и аналогичны
другим типам волн.
ЭМВ происходят колебания полей, а не вещества, как в случае
волн на воде или в натянутом шнуре.
4. Электромагнитная волна в вакууме распространяется со
скоростью света .
5. Электромагнитная волна переносит энергию, но и импульс.
(см гл. 5.5)

36. Шкала электромагнитных излучений.

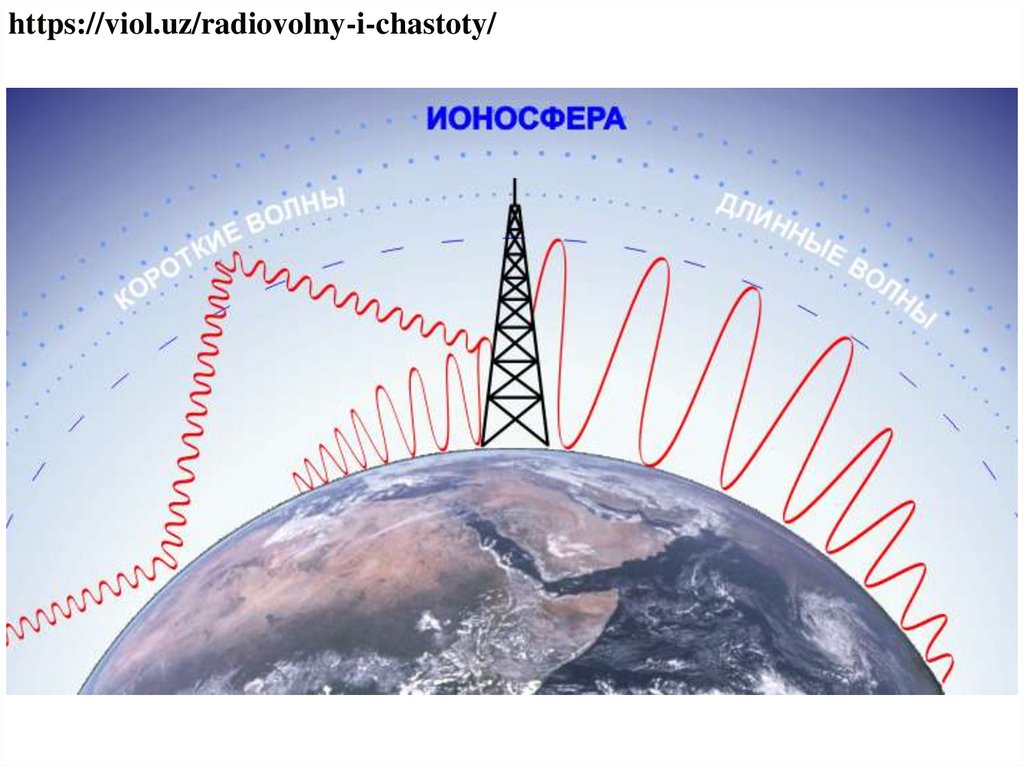
Шкала электромагнитных волн простирается от длинных
радиоволн до гамма – лучей.
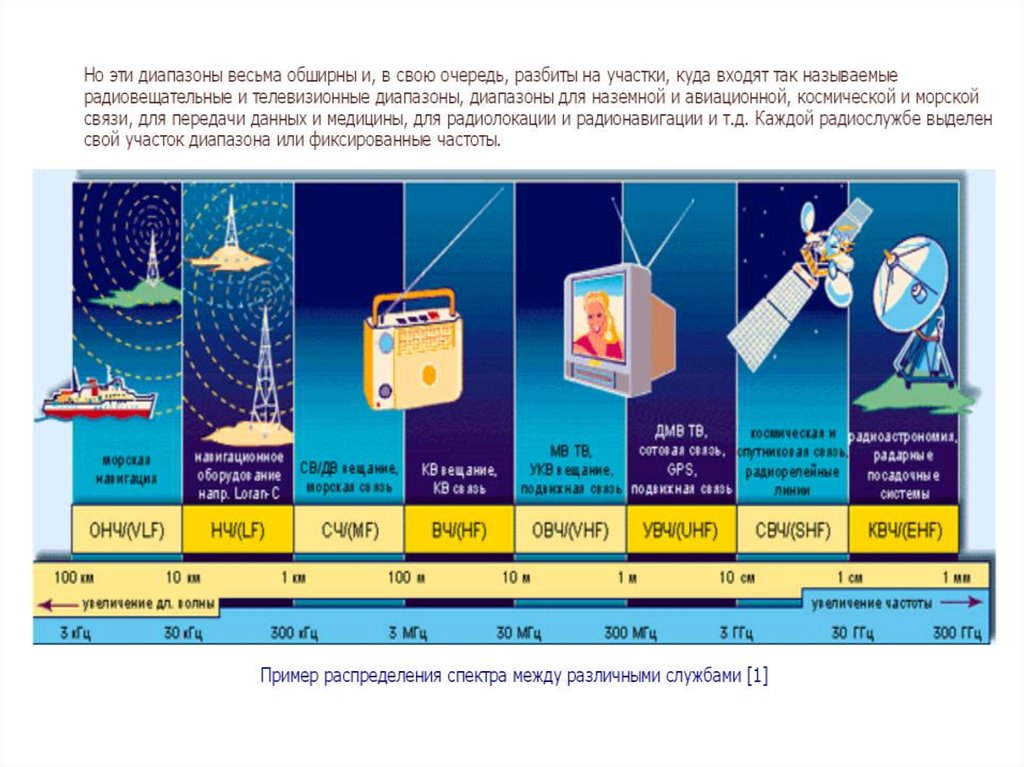
Электромагнитные волны различной длины условно делят
на диапазоны по различным признакам
( способу получения, способу регистрации, характеру
взаимодействия с веществом).
Все виды излучений имеют, по существу, одну и
ту же физическую природу.
Луи де Бройль

37.

Шкала электромагнитных волн
Видимый свет (в вакууме): λ = [380 (фиолетовый);
760 нм (красный)]

38.

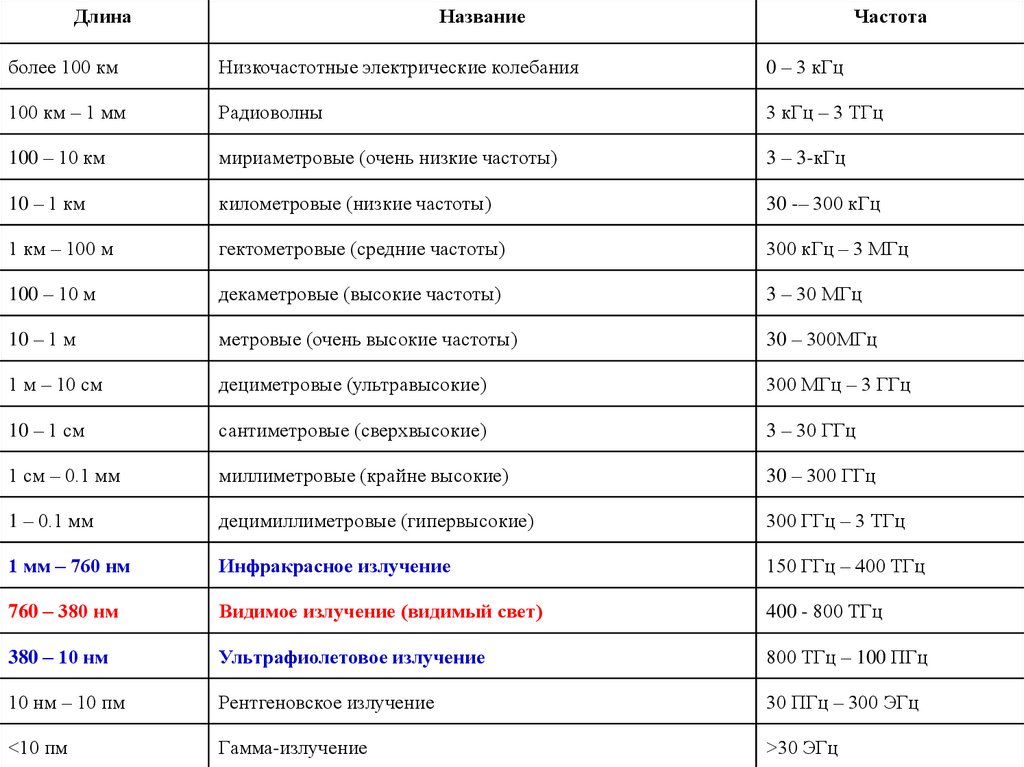
Длина
Название
Частота
более 100 км
Низкочастотные электрические колебания
0 – 3 кГц
100 км – 1 мм
Радиоволны
3 кГц – 3 ТГц
100 – 10 км
мириаметровые (очень низкие частоты)
3 – 3-кГц
10 – 1 км
километровые (низкие частоты)
30 -– 300 кГц
1 км – 100 м
гектометровые (средние частоты)
300 кГц – 3 МГц
100 – 10 м
декаметровые (высокие частоты)
3 – 30 МГц
10 – 1 м
метровые (очень высокие частоты)
30 – 300МГц
1 м – 10 см
дециметровые (ультравысокие)
300 МГц – 3 ГГц
10 – 1 см
сантиметровые (сверхвысокие)
3 – 30 ГГц
1 см – 0.1 мм
миллиметровые (крайне высокие)
30 – 300 ГГц
1 – 0.1 мм
децимиллиметровые (гипервысокие)
300 ГГц – 3 ТГц
1 мм – 760 нм
Инфракрасное излучение
150 ГГц – 400 ТГц
760 – 380 нм
Видимое излучение (видимый свет)
400 - 800 ТГц
380 – 10 нм
Ультрафиолетовое излучение
800 ТГц – 100 ПГц
10 нм – 10 пм
Рентгеновское излучение
30 ПГц – 300 ЭГц
<10 пм
Гамма-излучение
>30 ЭГц

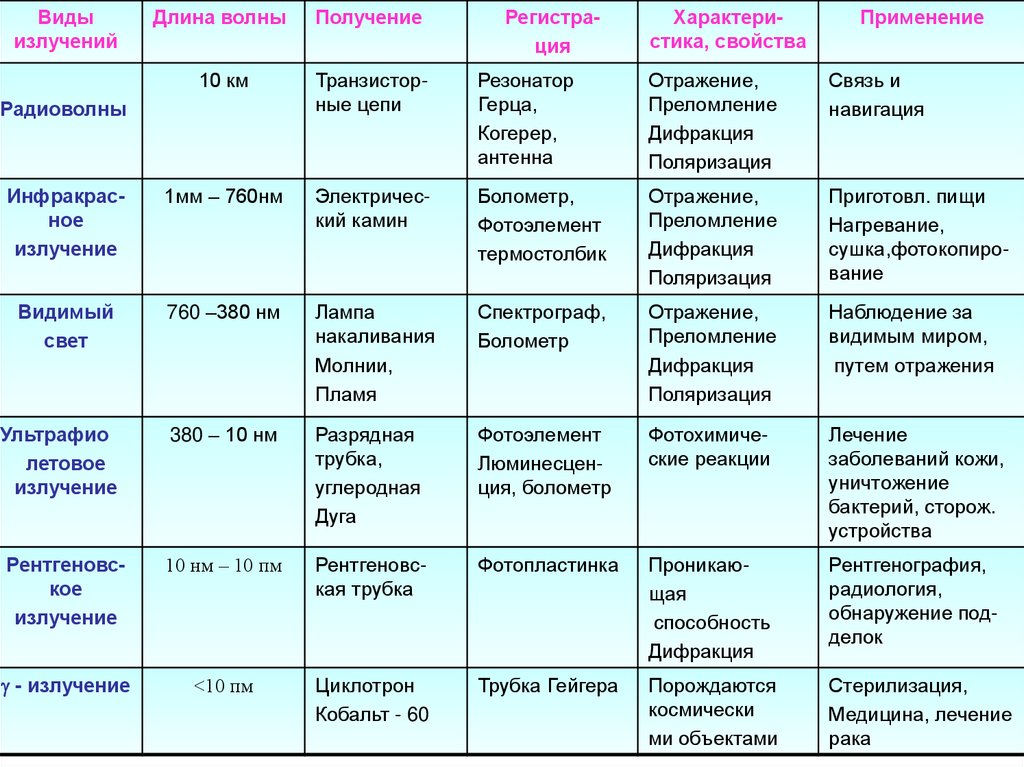
39.

Виды
излучений
Длина волны
Получение
10 км
Транзисторные цепи
Резонатор
Герца,
Когерер,
антенна
Отражение,
Преломление
Дифракция
Поляризация
Связь и
навигация
Инфракрасное
излучение
1мм – 760нм
Электрический камин
Болометр,
Фотоэлемент
термостолбик
Отражение,
Преломление
Дифракция
Поляризация
Приготовл. пищи
Нагревание,
сушка,фотокопирование
Видимый
свет
760 –380 нм
Лампа
накаливания
Молнии,
Пламя
Спектрограф,
Болометр
Отражение,
Преломление
Дифракция
Поляризация
Наблюдение за
видимым миром,
путем отражения
Ультрафио
летовое
излучение
380 – 10 нм
Разрядная
трубка,
углеродная
Дуга
Фотоэлемент
Люминесценция, болометр
Фотохимические реакции
Лечение
заболеваний кожи,
уничтожение
бактерий, сторож.
устройства
Рентгеновское
излучение
10 нм – 10 пм
Рентгеновская трубка
Фотопластинка
Проникающая
способность
Дифракция
Рентгенография,
радиология,
обнаружение подделок
- излучение
<10 пм
Циклотрон
Кобальт - 60
Трубка Гейгера
Порождаются
космически
ми объектами
Стерилизация,
Медицина, лечение
рака
Радиоволны
Регистрация
Характеристика, свойства
Применение

40.

41.

https://viol.uz/radiovolny-i-chastoty/

42.

43.

5.5 Энергия и импульс ЭМП
Распространение электромагнитных
волн связано с переносом энергии (подобно
тому, как распространение упругих волн в
веществе связано с переносом механической
энергии). Сама возможность обнаружения
ЭМВ указывает на то, что они переносят
энергию.

44.

Для характеристики переносимой
волной энергии русским ученым
Н.А.Умовым были введены понятия о
скорости и направлении движения
энергии, о потоке энергии. Спустя
десять лет после этого, в 1884 г.
английский ученый Джон Пойнтинг
описал процесс переноса энергии с
помощью
вектора
плотности
потока энергии.

45.

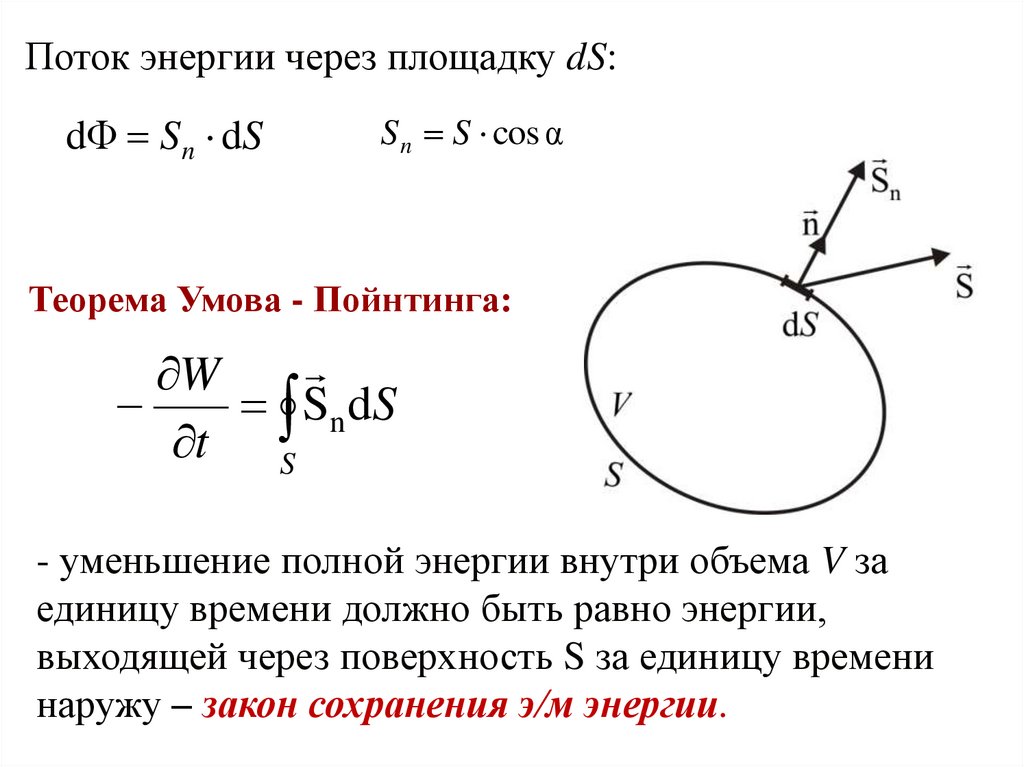
Поток энергии через площадку dS:
dΦ S n dS
S n S cos α
Теорема Умова - Пойнтинга:
W
Sn dS
t S
- уменьшение полной энергии внутри объема V за
единицу времени должно быть равно энергии,
выходящей через поверхность S за единицу времени
наружу – закон сохранения э/м энергии.

46.

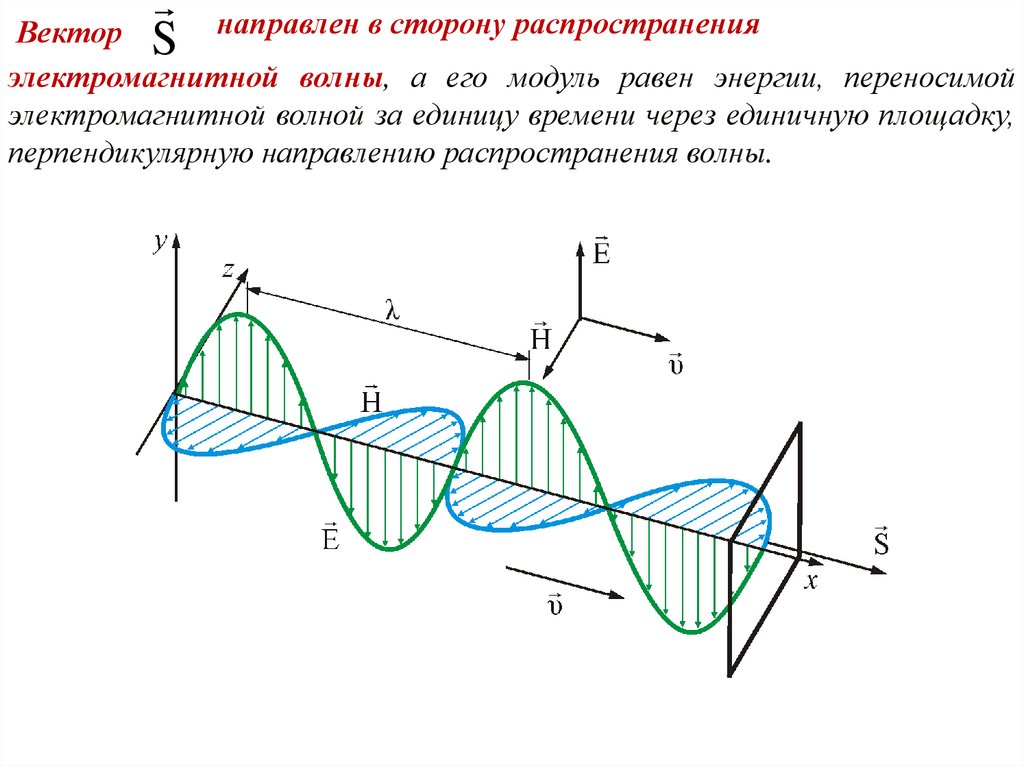
Вектор S
направлен в сторону распространения
электромагнитной волны, а его модуль равен энергии, переносимой
электромагнитной волной за единицу времени через единичную площадку,
перпендикулярную направлению распространения волны.

47.

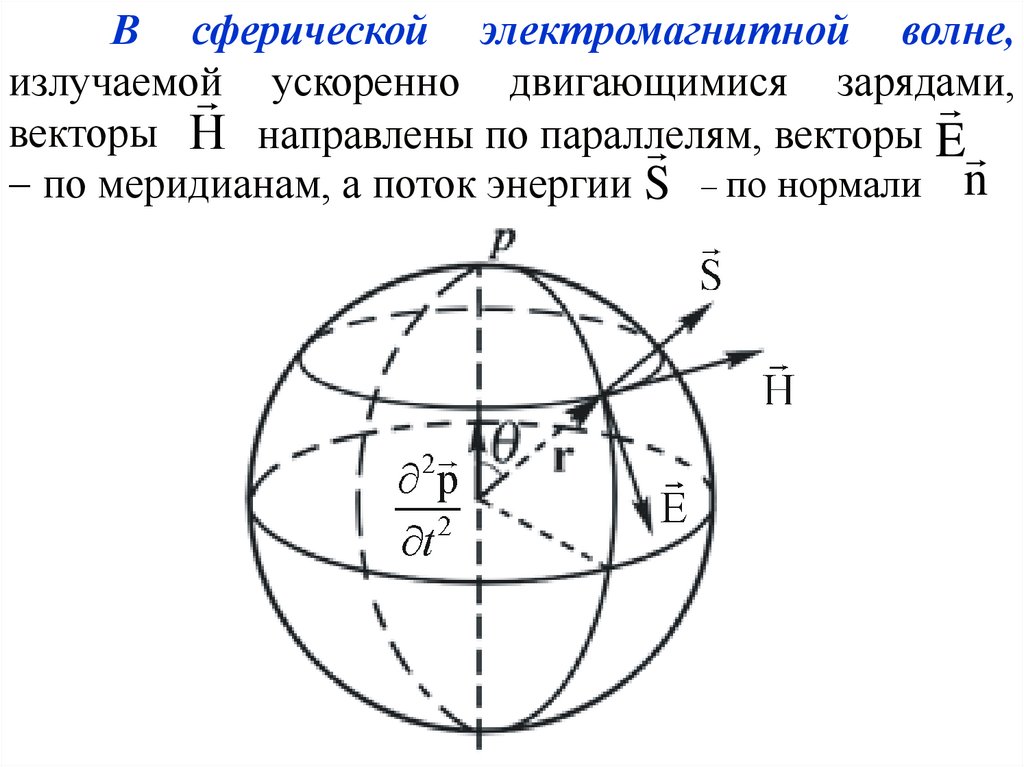
В сферической электромагнитной волне,
излучаемой
ускоренно двигающимися зарядами,
векторы Η направлены по параллелям,
векторы E
по меридианам, а поток энергии S по нормали n

48.

Интенсивность электромагнитной волны.
Для периодической электромагнитной волны модуль среднего значения
вектора Пойнтинга, (усреднение - по периоду волны) – это
интенсивность I :
1T
1
I S Sdt
T0
T
0 2 T 2
E cos t kx dt
0 m 0
При усреднении по периоду среднее значение квадрата косинуса
равно 1 2, следовательно, окончательно получится:
I S
1 0 2
E
2 0 m

49.

Импульс электромагнитной волны.
Перенос энергии электромагнитной волной сопровождается
переносом импульса. Импульс электромагнитного поля
где W - энергия электромагнитного поля.
P W c,
и
Запишем это выражение для плотностей импульса и энергии т.е., для
величин, отнесенных к единице объема: p w c
Если умножить и разделить числитель и знаменатель этого
выражения на с , получим в числителе плотность потока энергии wc ,
которая равна модулю вектора Пойнтинга.
1
p 2 E,H
c
Характеристики электромагнитной волны, такие как энергия, импульс
и интенсивность присущи любому типу волн, например, упругим.
Если учесть свойства среды, в которой распространяются упругие
волны, то легко получить выражения для этих характеристик.

50.

Излучение электрического диполя.
Возбуждение электромагнитных волн какой-либо системой называют
излучением этих волн, а саму систему – излучающей системой.
В соответствии с представлениями классической электродинамики
электромагнитные волны в вакууме возбуждаются электрическими
зарядами, движущимися с ускорением.
Простейшей
излучающей системой является электрический диполь,
момент p которого изменяется с течением времени.
Вспомним, что электрическим диполем называется система двух
одинаковых по абсолютной величине разноименных точечных зарядов
q и q .
Электрический момент диполя это вектор, направленный по оси
диполя от отрицательного заряда к положительному:
p ql

51.

Излучение электрического диполя.
Пусть момент p диполя изменяется по гармоническому закону:
p p0 cos t
Это излучение простейшего гармонического осциллятора.
Рассмотрим некоторые закономерности излучения электрического
диполя.
А). Электрическое поле постоянного диполя спадает при удалении .
от диполя по закону 1 r 3 .
В случае осциллирующего диполя ситуация изменяется.
Вблизи диполя картина электрического поля сложна. Однако на
расстояниях r λ (в так называемой волновой зоне) можно
рассматривать только поле осциллирующих зарядов.
В волновой зоне сохранится расходящаяся сферическая волна с
той же частотой, что и у осциллятора.

52.

Излучение электрического диполя.
Амплитуда волны уменьшается с ростом расстояния r от диполя как
1
.sin , где (тета) – угол между осью диполя и радиус – вектором r
r
точки O , где наблюдается поле.
О
Диполь
Б). Интенсивность I электромагнитной
волны пропорциональна произведению
. m H m, следовательно, пропорциональна
E
1
I ~ 2 sin 2
r
I
Зависимость
наглядно
изображается с помощью диаграммы
направленности излучения диполя.

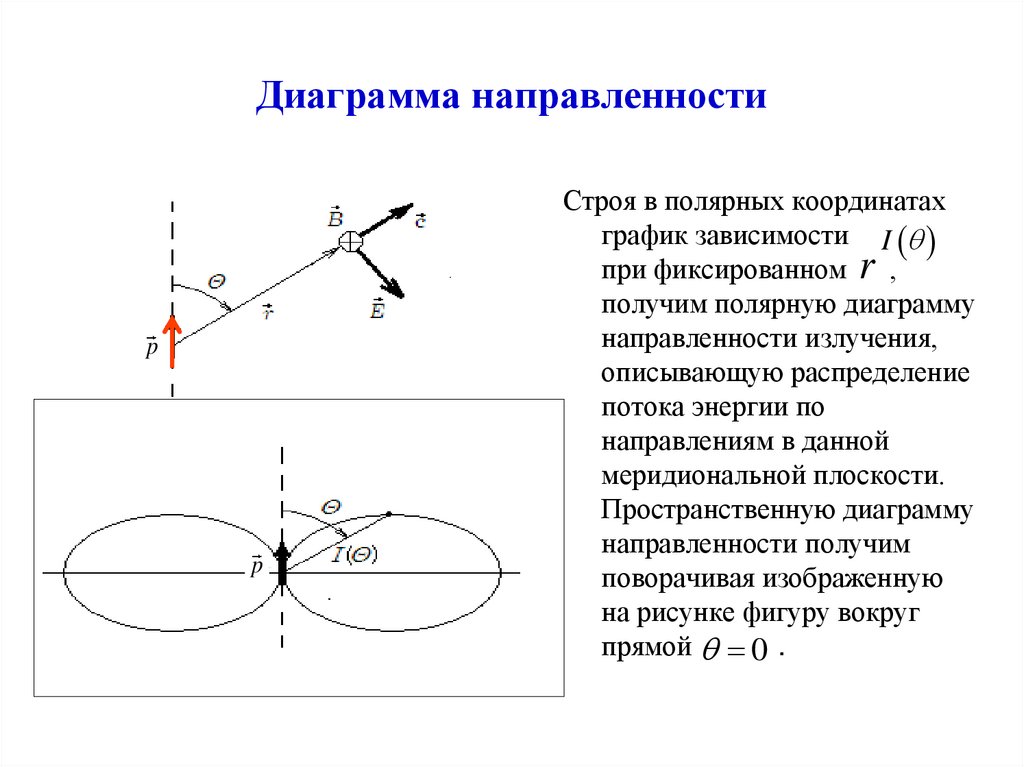
53. Диаграмма направленности

p
p
Строя в полярных координатах
график зависимости I
при фиксированном r ,
получим полярную диаграмму
направленности излучения,
описывающую распределение
потока энергии по
направлениям в данной
меридиональной плоскости.
Пространственную диаграмму
направленности получим
поворачивая изображенную
на рисунке фигуру вокруг
прямой 0 .

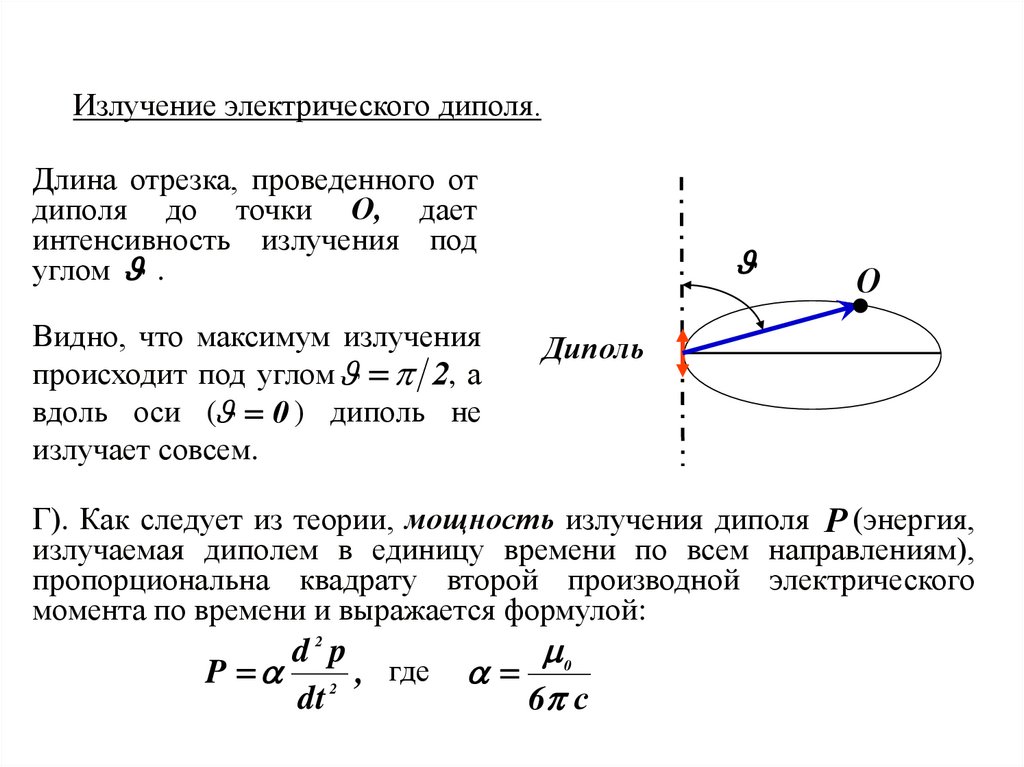
54.

Излучение электрического диполя.
Длина отрезка, проведенного от
диполя до точки О, дает
интенсивность излучения под
углом .
Видно, что максимум излучения
происходит под углом 2, а
вдоль оси ( 0 ) диполь не
излучает совсем.
О
Диполь
Г). Как следует из теории, мощность излучения диполя P (энергия,
излучаемая диполем в единицу времени по всем направлениям),
пропорциональна квадрату второй производной электрического
момента по времени и выражается формулой:
d2 p
P 2 , где
dt
0
6 с

55.

Излучение электрического диполя.
Поскольку зависимость p t задана гармонической функцией,
выражение для мощности излучения диполя можно записать в виде:
P 4 pm2 cos 2 t
Средняя по времени мощность излучения
О
P
2
4 pm2 ~ 4 pm2
Важный вывод: средняя мощность излучения
осциллирующего диполя зависит от квадрата
его амплитуды и сильно от частоты (~ 4 ).
Таким образом, излучение линий передач
промышленной частоты мало, а радиостанции
должны использовать высокие частоты.
Значение задачи об излучении диполя: всякую реальную излучающую
систему (например, антенну) можно рассматривать как совокупность
точечных диполей.
Излучение антенны в целом есть суперпозиция излучений отдельных
диполей, с помощью которых моделируется антенна.

56.

Излучение электрического диполя.
Поскольку зависимость p t задана гармонической функцией,
выражение для мощности излучения диполя можно записать в виде:
P 4 pm2 cos 2 t
Средняя по времени мощность излучения
О
P
2
4 pm2 ~ 4 pm2
Важный вывод: средняя мощность излучения
осциллирующего диполя зависит от квадрата
его амплитуды и сильно от частоты (~ 4 ).
Таким образом, излучение линий передач
промышленной частоты мало, а радиостанции
должны использовать высокие частоты.
Значение задачи об излучении диполя: всякую реальную излучающую
систему (например, антенну) можно рассматривать как совокупность
точечных диполей.
Излучение антенны в целом есть суперпозиция излучений отдельных
диполей, с помощью которых моделируется антенна.

57. Момент импульса электромагнитной волны (СРС *)

• В 1889г А.И.Садовский теоретически предсказал, что свет,
поляризованный по кругу или эллиптически (см. лекцию
по поляризации) должен обладать моментом импульса.
Экспериментально наличие момента импульса у
электромагнитной волны обнаружили в 1935-36гг
Холборн (Англия) и Бет (США).