Similar presentations:
Формула с татуировкой Ньютона
1. Формула с татуировкой Ньютона
2.
История развития ДМ. ЗадачиПринцип Дирихле
Основные правила комбинаторики
Выборки. Комбинаторные числа
Метод включений и исключений
Бином Ньютона. Полиномиальная формула
Рекуррентные соотношения
Производящие функции
3. БИНОМ НЬЮТОНА
4.
5.
(a + b)2 = a2 + 2ab + b2;(a + b)3 = a3 + 3a2b + 3ab2 + b3.
Эти равенства являются частными случаями
общей формулы, дающей разложение (a + b)n.
6.
7.
8.
(a + b)n = (a + b)(a + b) … (a + b).Раскроем скобки в правой части этого равенства, записывая множители в
том порядке, в котором они встречаются.
Например, (a + b)2 = (a + b)(a + b) = aa + ab + ba + bb;
(a + b)3= (a + b)(a + b)(a + b) = aaa + aab + aba + abb + baa +
+ bab + bba + bbb.
Таким образом, после раскрытия скобок получатся всевозможные
размещения с повторениями из 2 букв a и b, состоящие из n элементов.
9.
Приведем подобные члены. Подобными будут члены, содержащиеодинаковое количество букв b (тогда и букв a в них будет поровну).
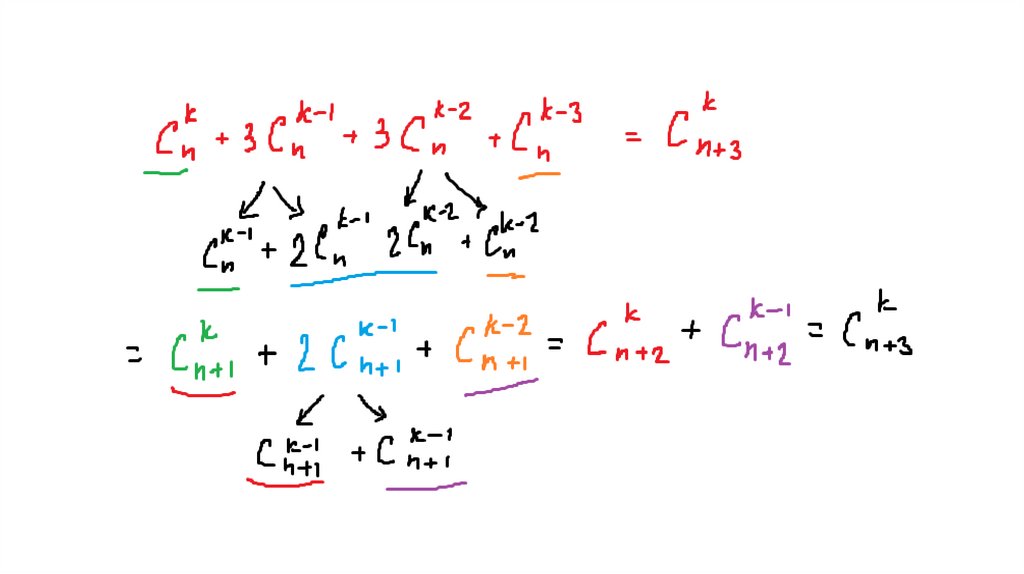
Найдем число членов, в которые входит k букв b и, следовательно,
n – k букв a.
Эти члены являются перестановками с повторениями, составленными
из k букв b и n – k букв a. Поэтому их число равно
.
n!
k
P(k , n k )
Cn
(n k )! k!
10.
11.
Таким образом:(a b)
n
0 n
1 n 1
k n k k
n n
C n a C n a b ... C n a b ... C n b
Это равенство принято называть формулой бинома Ньютона.
.
12.
13. Свойства биномиальных коэффициентов
14.
15. 1
16. 2 В формуле бинома Ньютона наибольшее значение имеют центральные коэффициенты. Если n = 2m, то наибольшее значение имеет
2В формуле бинома Ньютона наибольшее значение
имеют центральные коэффициенты. Если n = 2m, то m
наибольшее значение имеет (m + 1)-й коэффициент C2 m
если n = 2m + 1, то наибольшее значение имеют два
коэффициента:
m
m 1
C 2 m 1
C 2 m 1
17.
18.
19. 3 Тождество Паскаля
20. 4 Упражнение Доказать формулу бинома Ньютона методом математической индукции (используя тождество Паскаля)
21. 5 Упражнение Доказать тождество Паскаля с помощью соотношения
22.
23.
24.
25.
26.
27. 6
28.
29.
30.
31. 7
32.
Пример 1. В разложении7
b
a
10 3
a
b
имеется член, содержащий ab.
Найти этот член.
n
33.
Используя формулу бинома Ньютона, получаем, чтообщий член разложения имеет вид
k b
Cn
a
n k
7
a
10
b3
k
6 n
n 4
k
k
k
5
2
2
5
Cn a
b
34.
Общий член будет содержать ab, если показатели степени6
n
k
5
2
n 4
k
2 5
равны единице,
следовательно, n и k должны удовлетворять системе
n
6
k
1
5
2
n 4 k 1.
2 5
Решив эту систему, получим n = 10, k = 5
C ab 252ab.
5
10
35.
Пример 3. Найти все рациональные члены разложения1 3
2
2
20
, не выписывая иррациональные.
36.
Это число будет рациональным, если показатель – целое число.37.
Это возможно при k = 0, k = 6, k = 12, k = 18Следовательно, соответствующими членами разложения будут
0 10
C20 2
1
1024
C 125970
12
20
6
C
4845
6 5
20
C20 2
32
4
C 2 32C 6080
18
20
5
18
20
38.
Пример 4. Найти, не раскрывая скобок, коэффициент при х9 вмногочлене
(1 + х)9 + (1 + х)10 + (1 + х)11 + (1 + х)12 + (1 + х)13+ (1 + х)14.
39.
Общий член разложения (1+х)n имеет видn k
C 1
k
n
x C x
k
k
n
k
поэтому в разложении (1 + х)9 коэффициент при х9 равен
в разложении (1 + х)10 коэффициент при х9 равен
…, в разложении (1 + х)14 коэффициент при х9 равен
Отсюда получаем, что коэффициент при х9 равен
9
9
9
C9 C10 ... C14 3003.
9
C9
9
10
C
9
C14
40.
Пример 6. Найти член разложения бинома( x 4 x 3 )n
содержащий x6,5, если 10-й член разложения имеет наибольший
биномиальный коэффициент.
41.
Так как 10-й член разложения имеет наибольшийбиномиальный коэффициент, то m = 10 – 1 = 9, а
n = 2m = 18.
Общий член разложения имеет вид
k
C18
5k
9
18 k 4 3 k
k
4
x
x
C18 x
5k
9
6,5
4
2 6, 5
18
C x
153x .
6, 5
42.
Пример 9. Вычислить суммуC 2C 3C ... nC
1
n
2
n
3
n
n
n
43.
Обозначимn 1
n
S C 2C 3C ... (n 1)C
1
n
2
n
3
n
Воспользовавшись
коэффициентов
k
получим
Cn C
свойством
nC
n
n
биномиальных
n k
n
n 1
n 2
1
0
S Cn 2Cn ... (n 1)Cn nCn
44.
Сложим эти равенства2S nC C (n 1)C 2C (n 2)C ... nC
0
n
1
n
1
n
2
n
2
n
n
n
0
1
2
n
0
1
n
n
nCn nCn nCn ... nCn n(Cn Cn ... Cn ) n 2
Отсюда получаем
1
n
n 1
S n 2 n 2
2
45.
46.
47.
48.
49. 13 Доказать
50.
51.
52.
53. 14 Показать, что при любом k сумма есть точный квадрат
54.
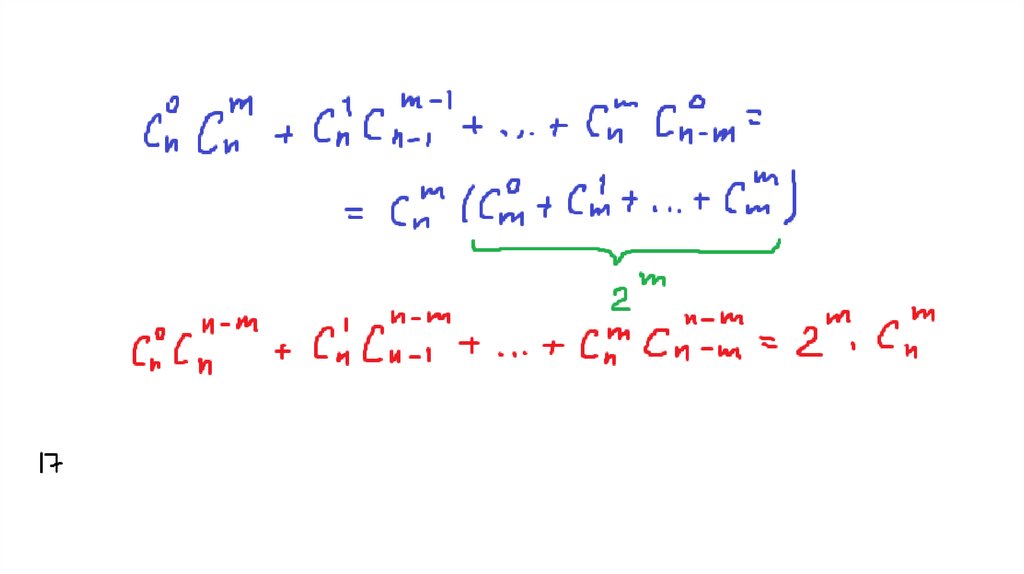
55. 15 Доказать, что
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69. 24 Доказать, что
70.
71. ИЗВЛЕЧЕНИЕ КОРНЕЙ
72.
mОпределим Cn для любых значений n и m так, чтобы почти
все их свойства сохранились и после такого обобщения. Для этого
m
C
запишем n в следующем виде:
n(n 1)...( n m 1)
m
Cn
.
1 2 ... m
73.
1Формула Ньютона при n примет вид
2
1 1
1 1 1
1
1
1 2
1
2 2 2 2 2 2
x3
2
(1 x) 1 x
x
2
1 2
1 2 3
1 1 1
1 ... k 1
2 2 2
x k ...
1 2 ... k
74.
После преобразования этого выражения, получаем1
1
2
(1 x) 1 x
2
1 2
1 3 3
x
x ...
2 4
2 4 6
k 1 1 3 ... ( 2k 3) k
... ( 1)
x ...
2 4 ... 2k
75.
11
2
(1 x) 1 x
2
1
2 2
1 2
С x
3 2
1
3 2
2 3
С x ...
5 4
...
( 1)
k 2
k 1
k 1 k
C
x
...,
2
k
2
2k 1
76.
Например:30
1
25 5 5 1 0,2 5(1 0,2) 2
1
1 3
1
2
3
5 1 0,2
0,2
0,2 5,4775.
2 4
2 4 6
2



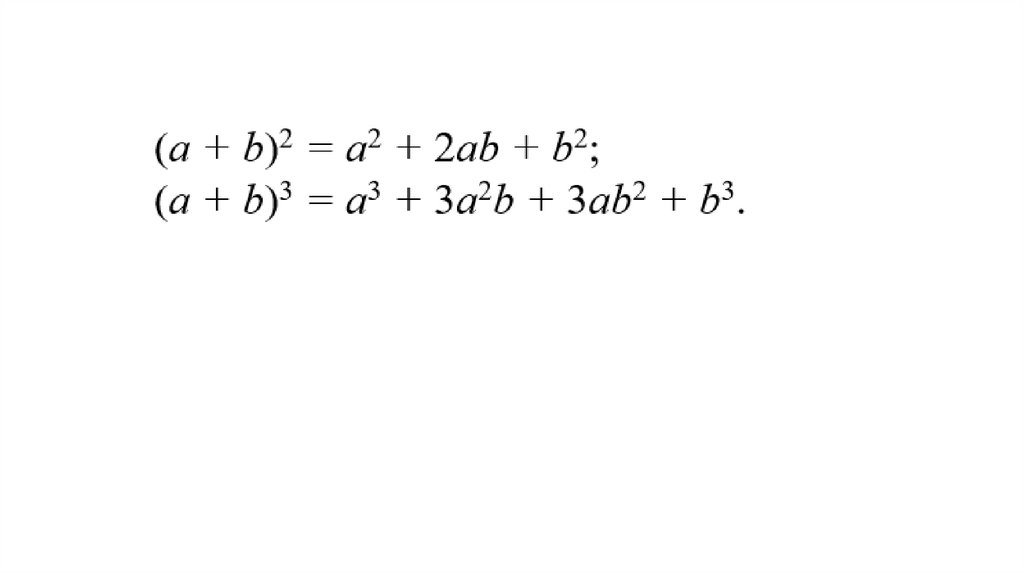









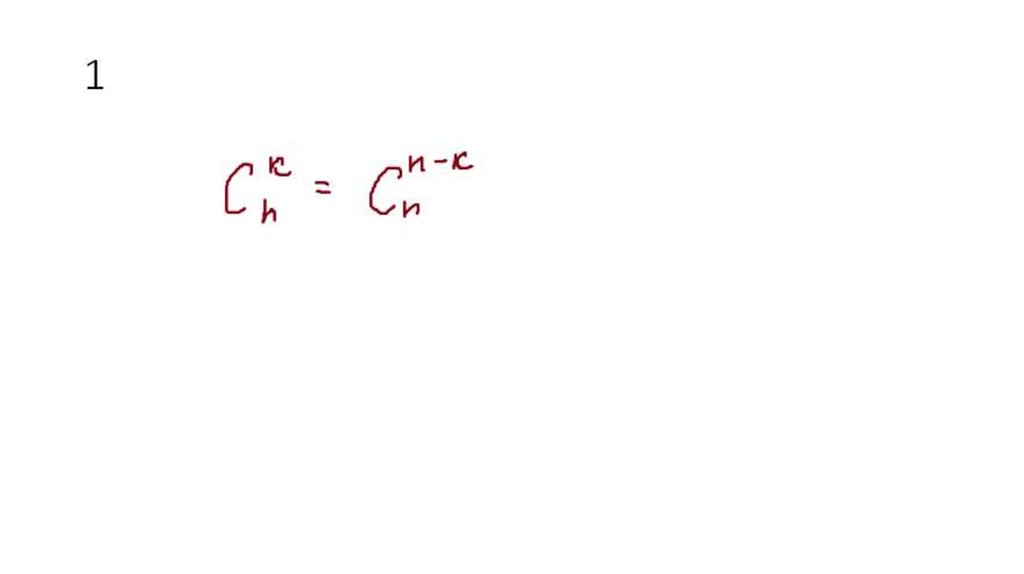
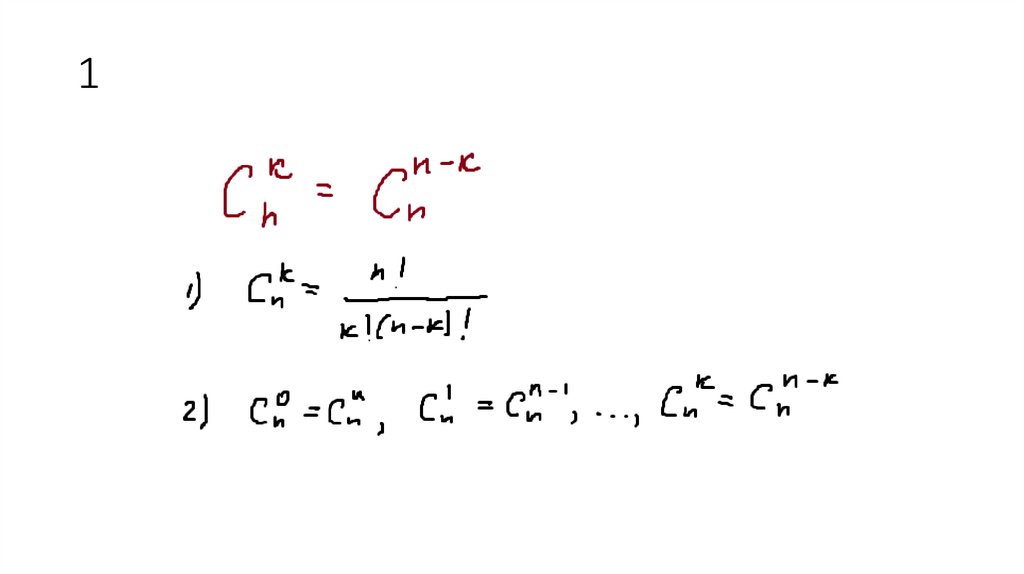







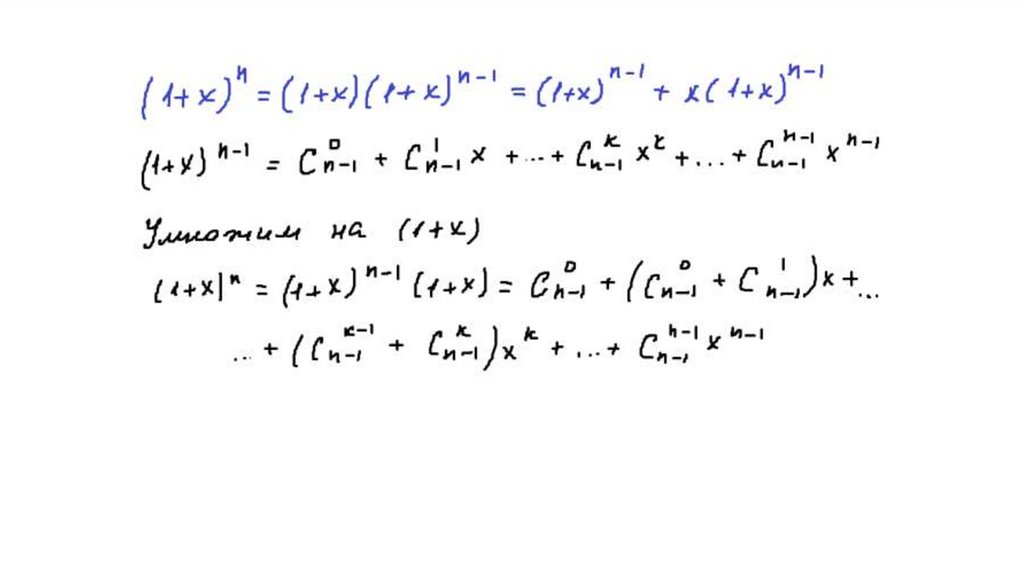
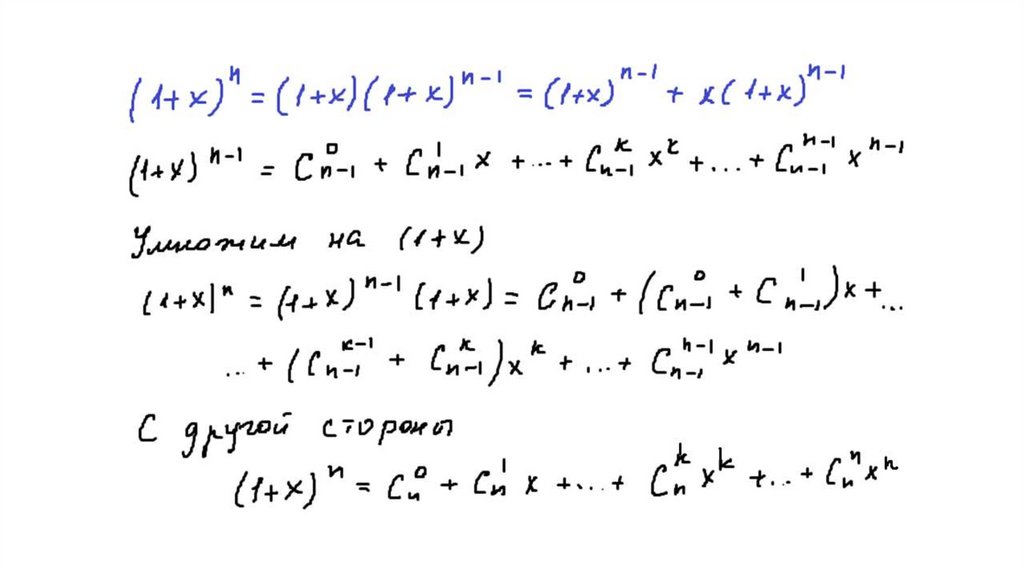
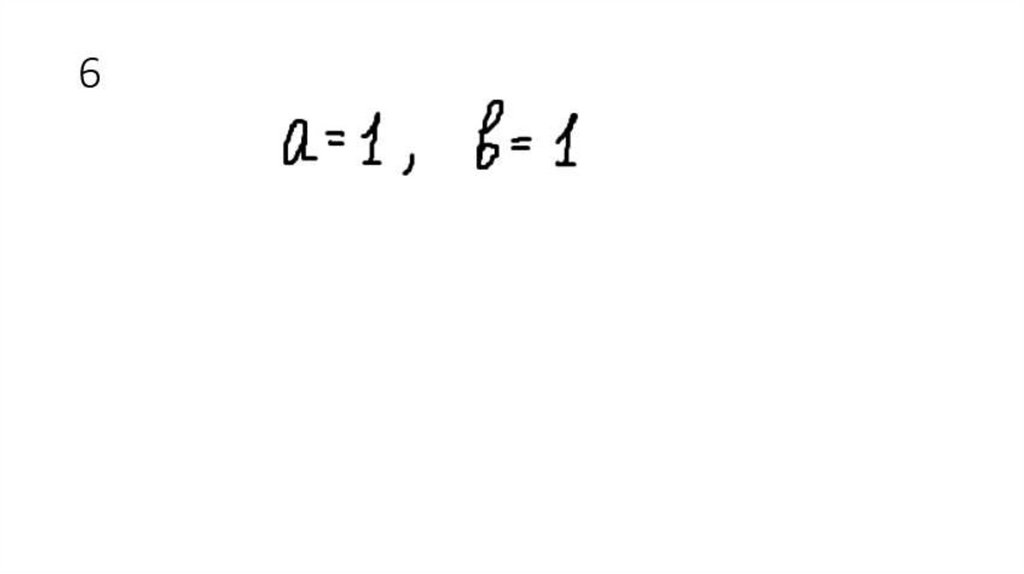
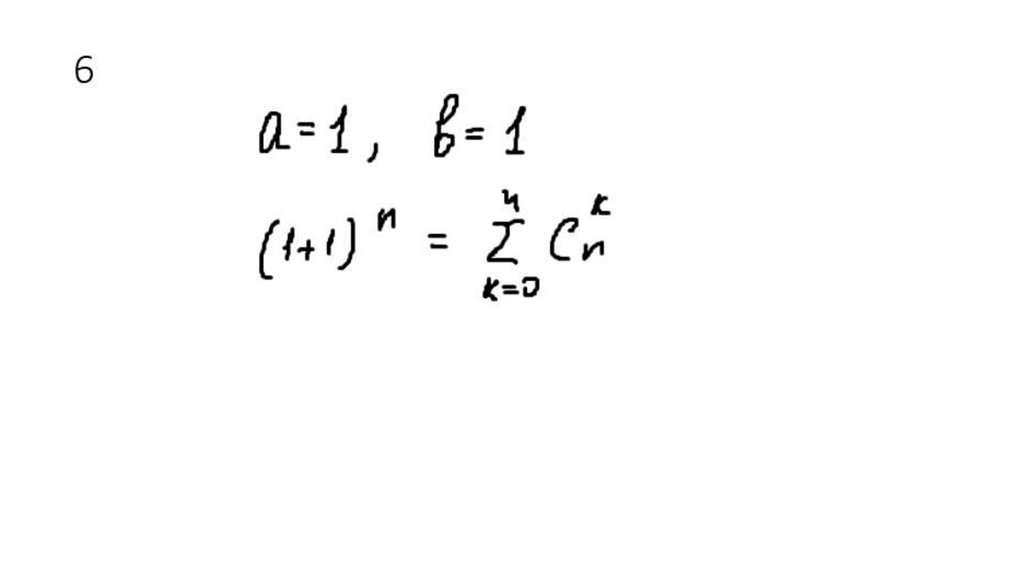
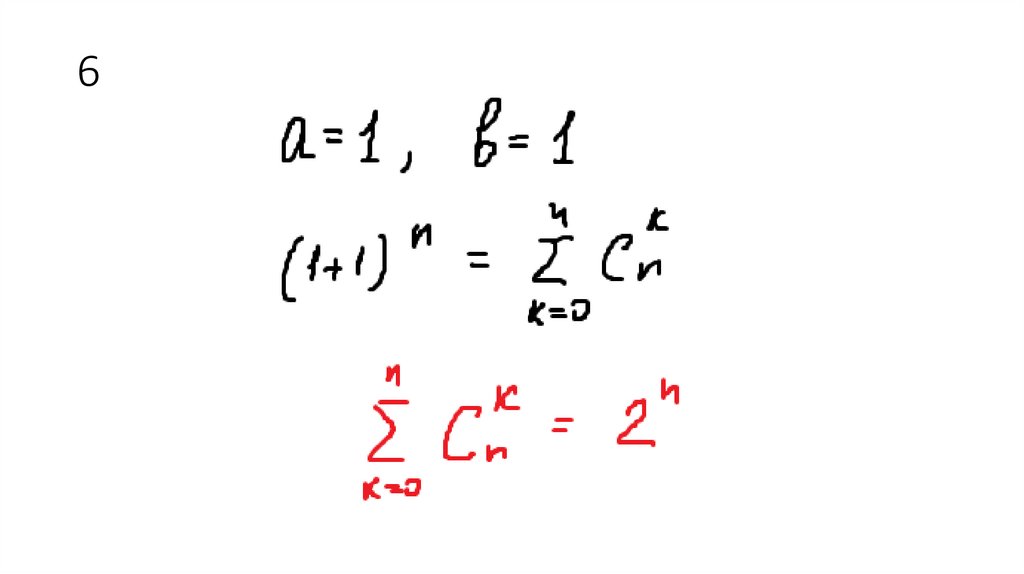
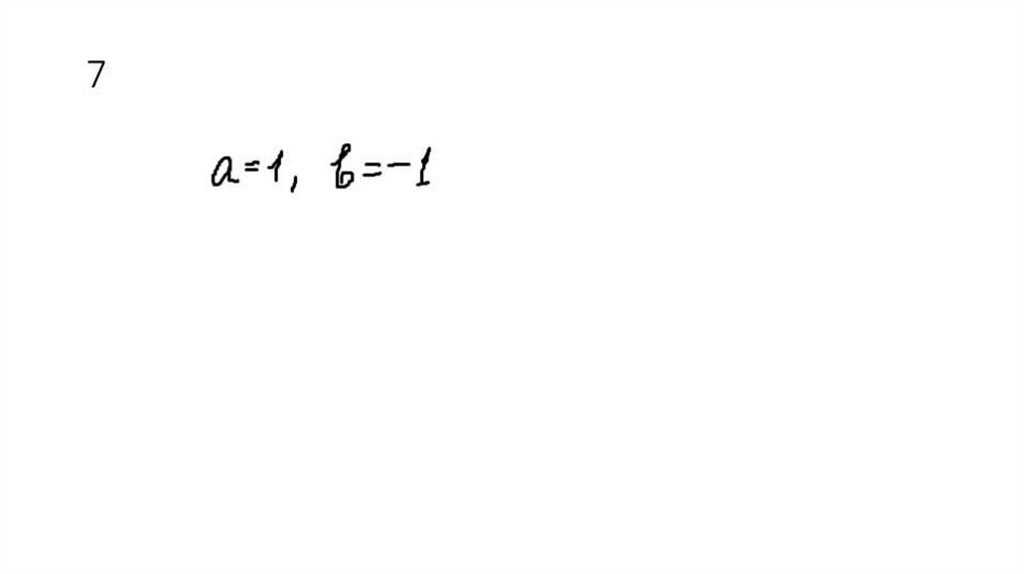
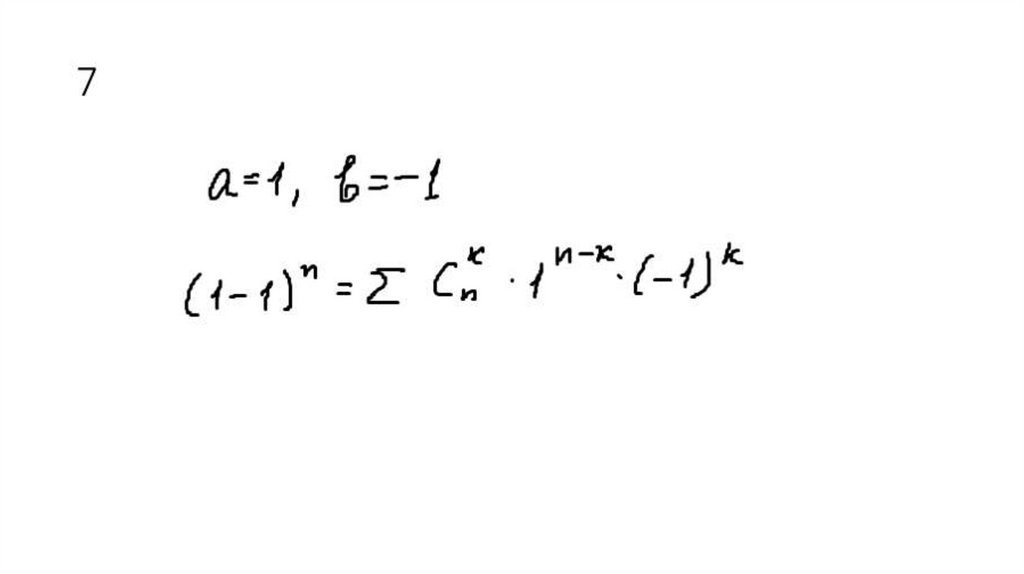
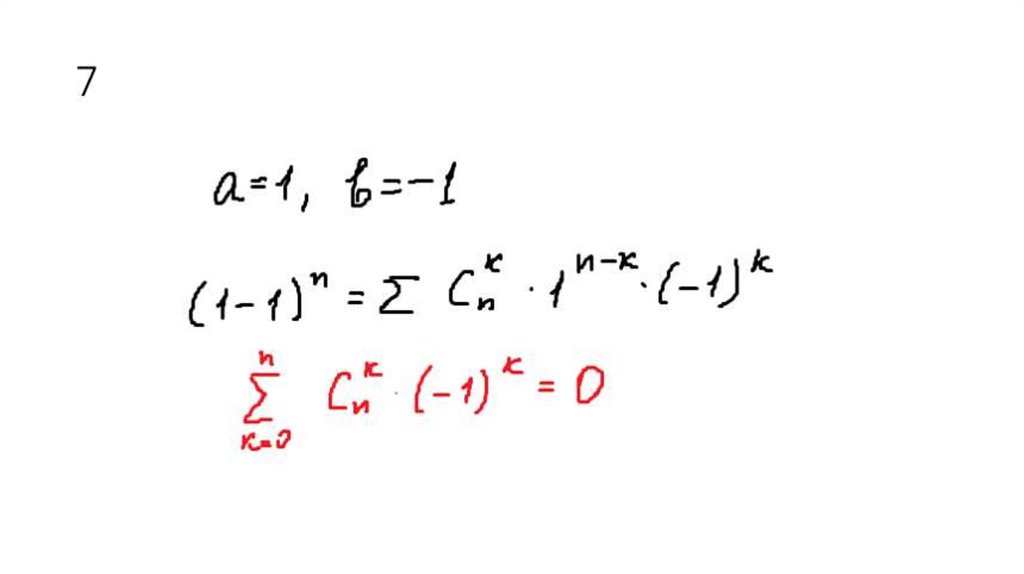
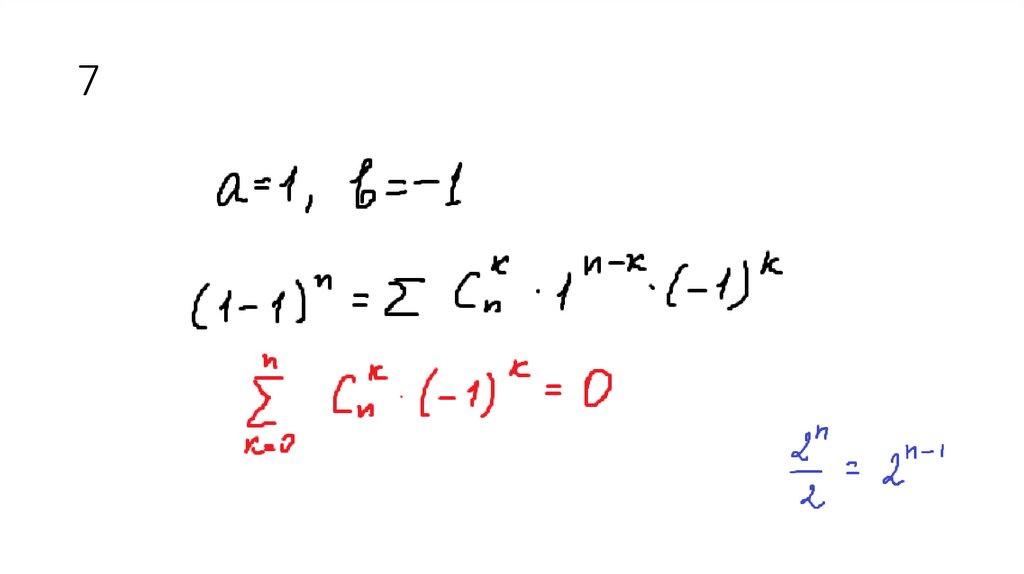










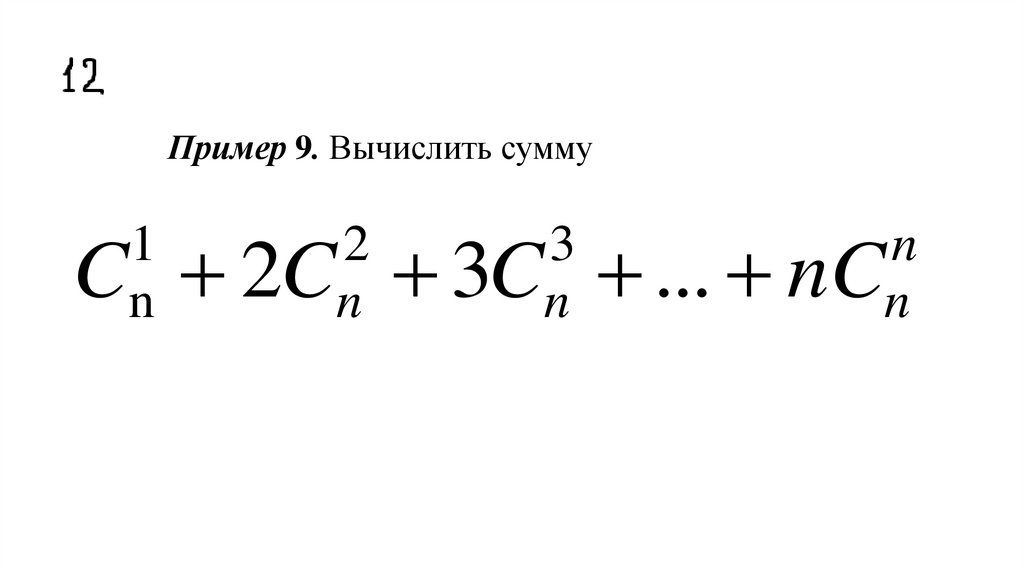


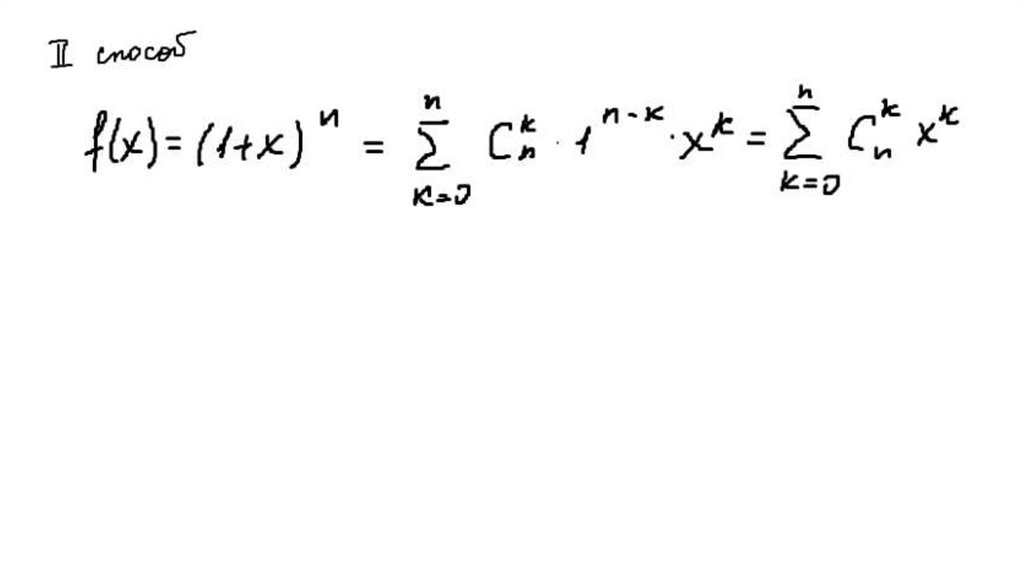
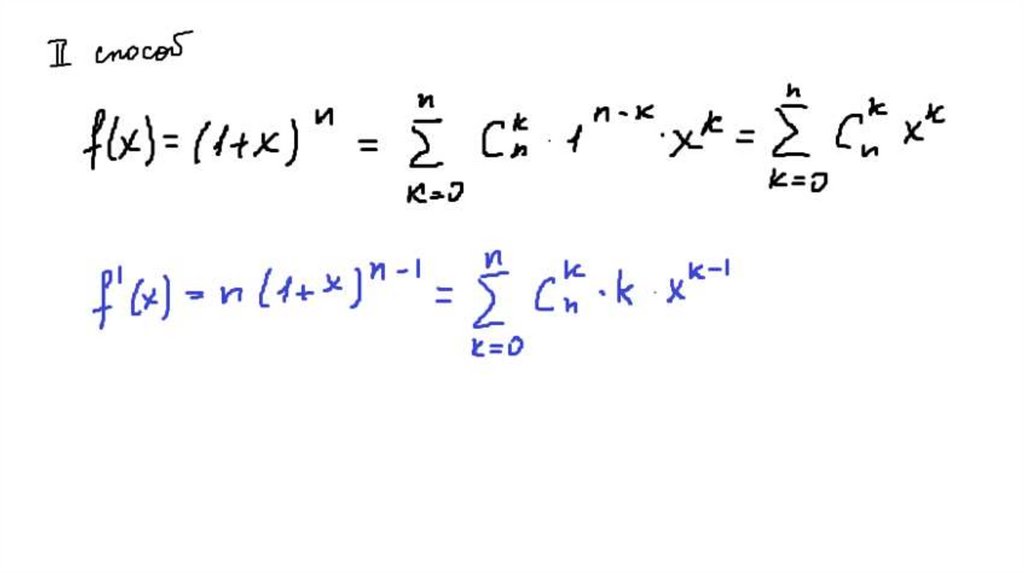
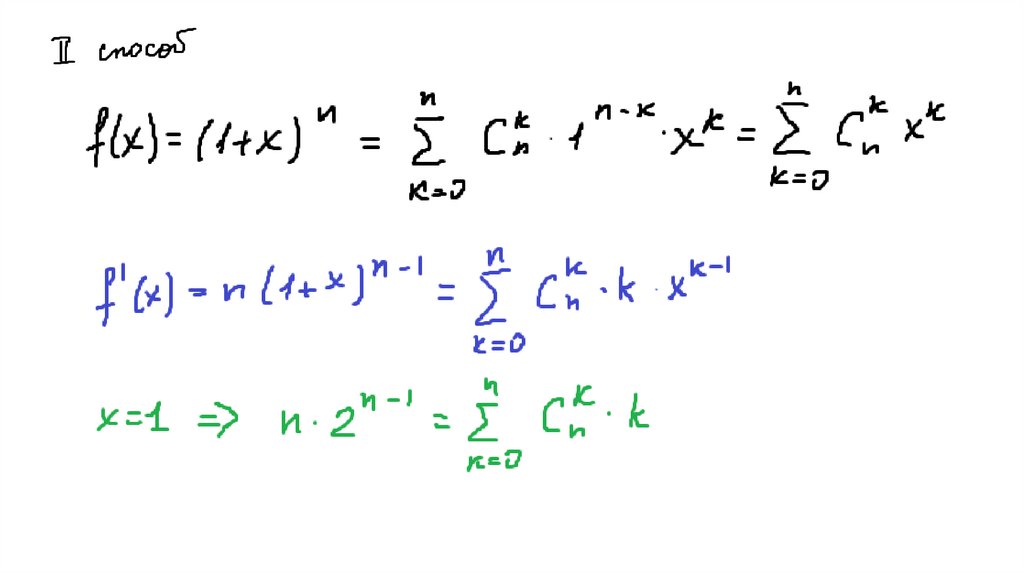

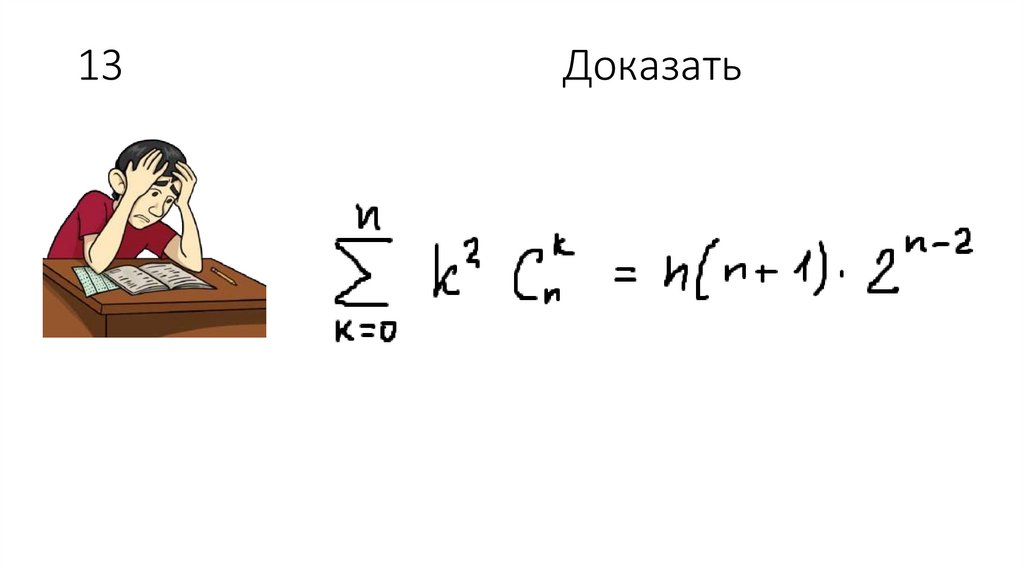

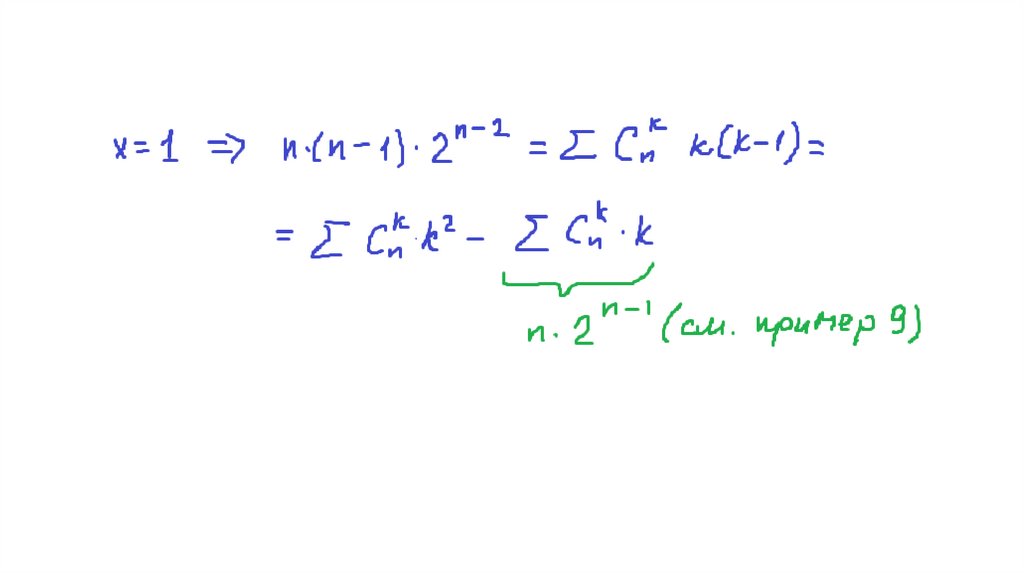
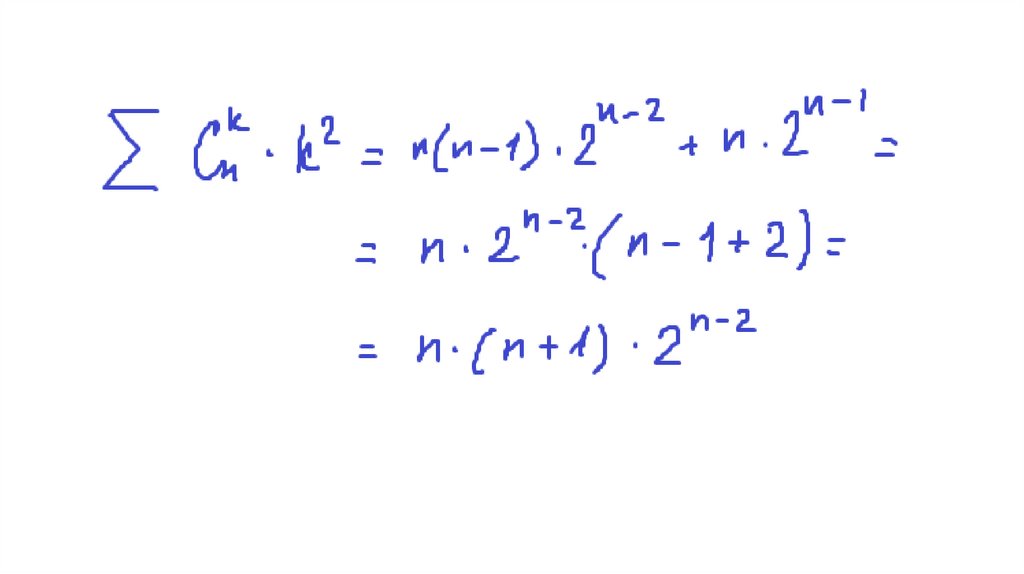

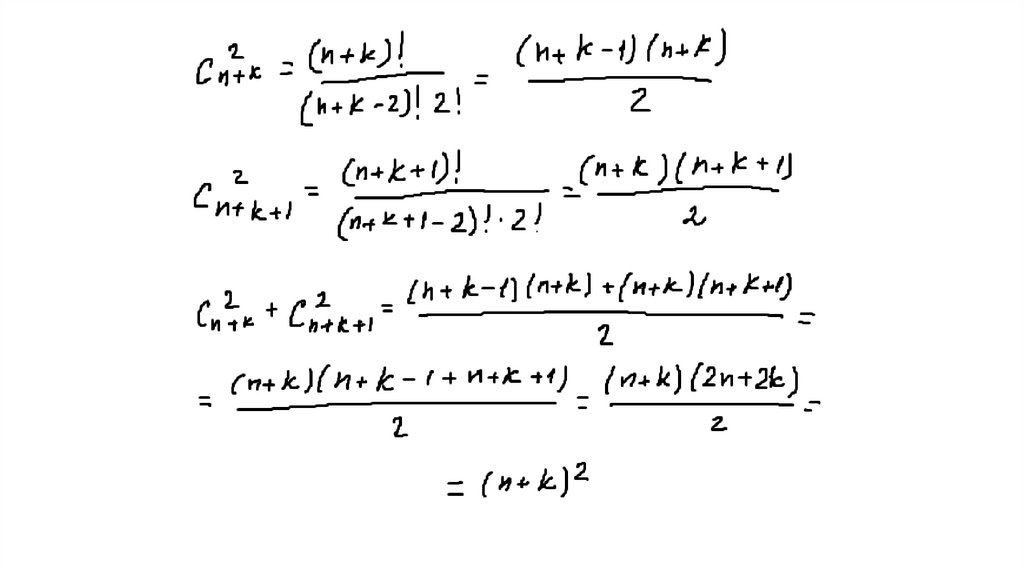
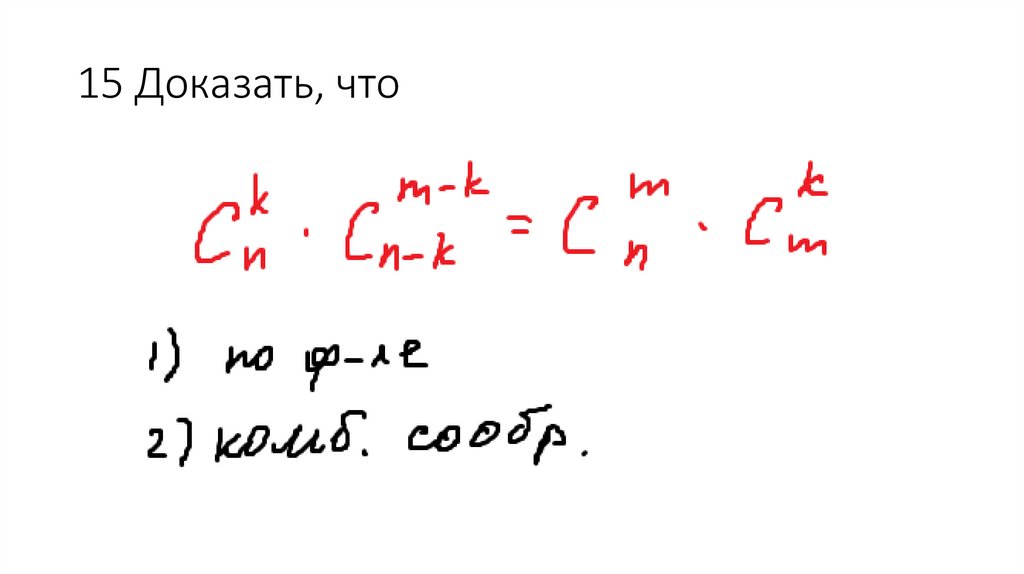
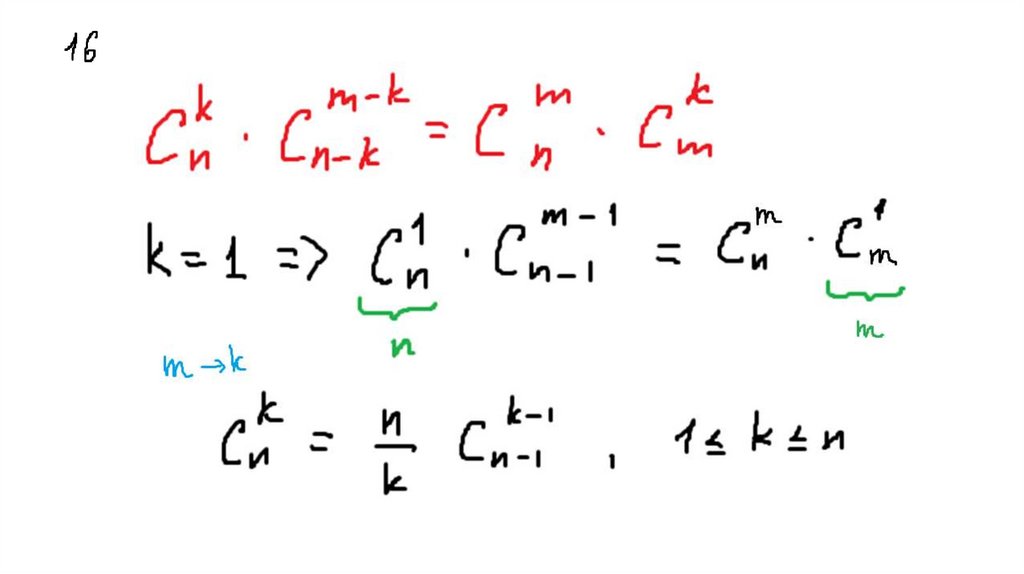
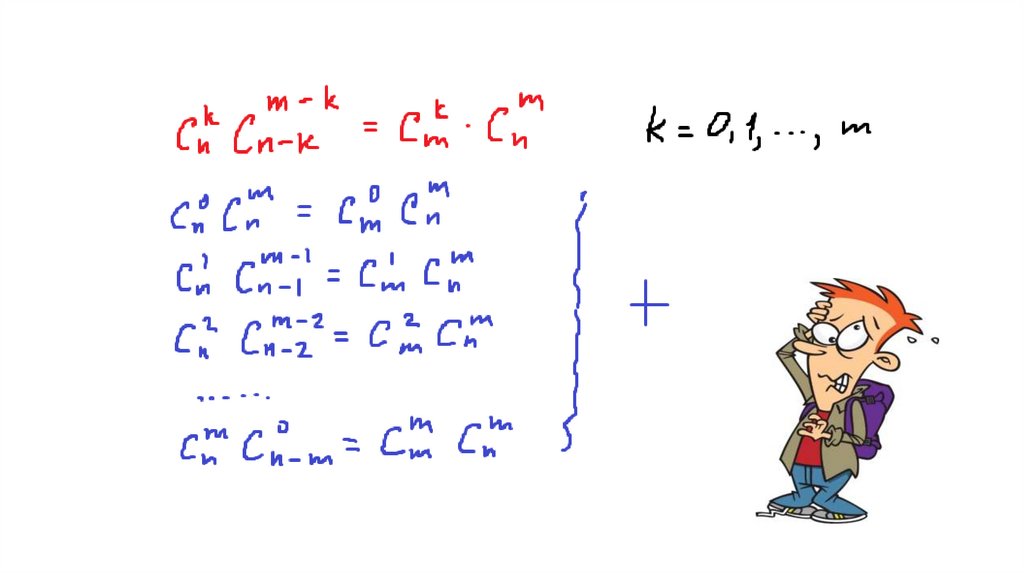

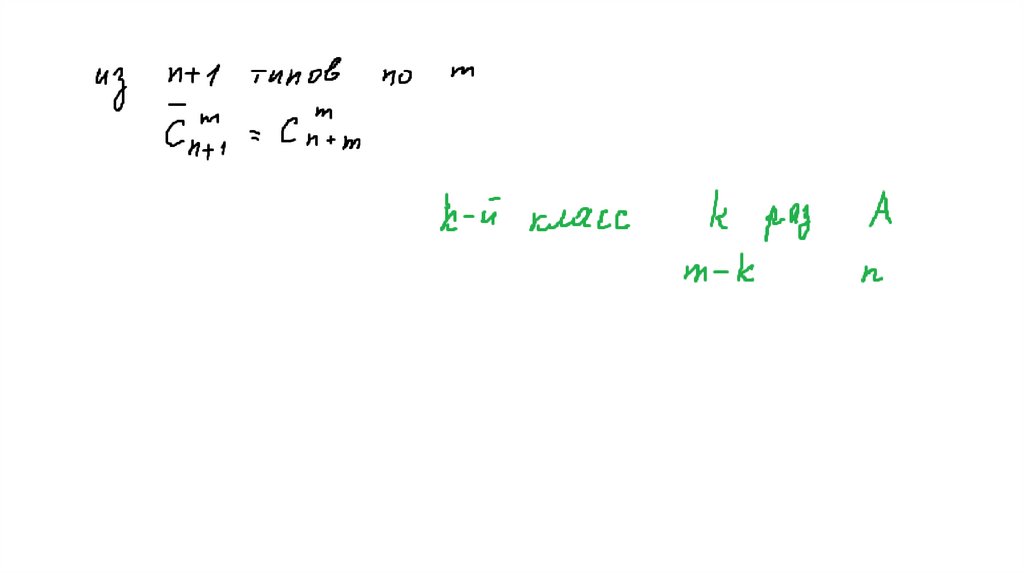
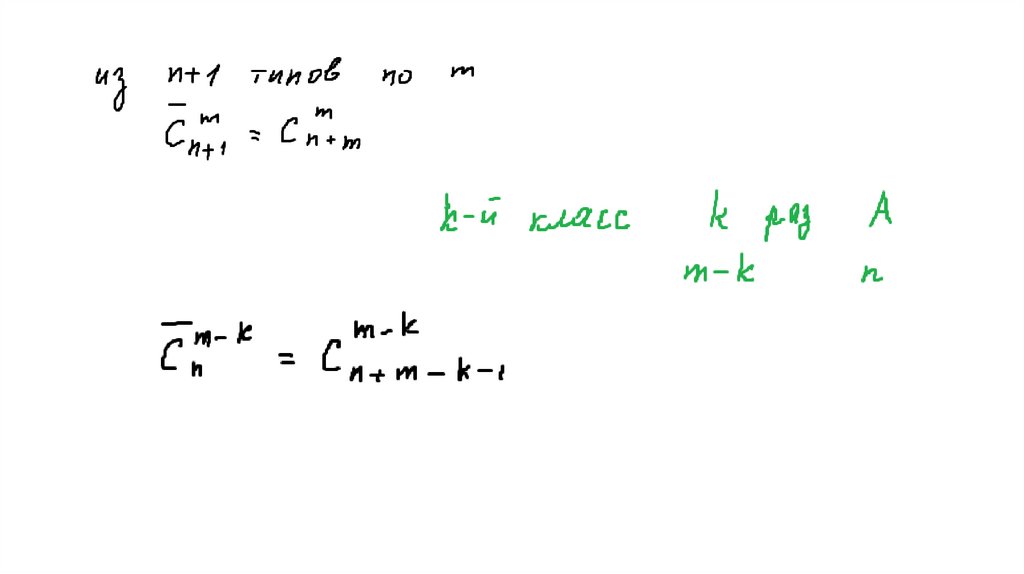
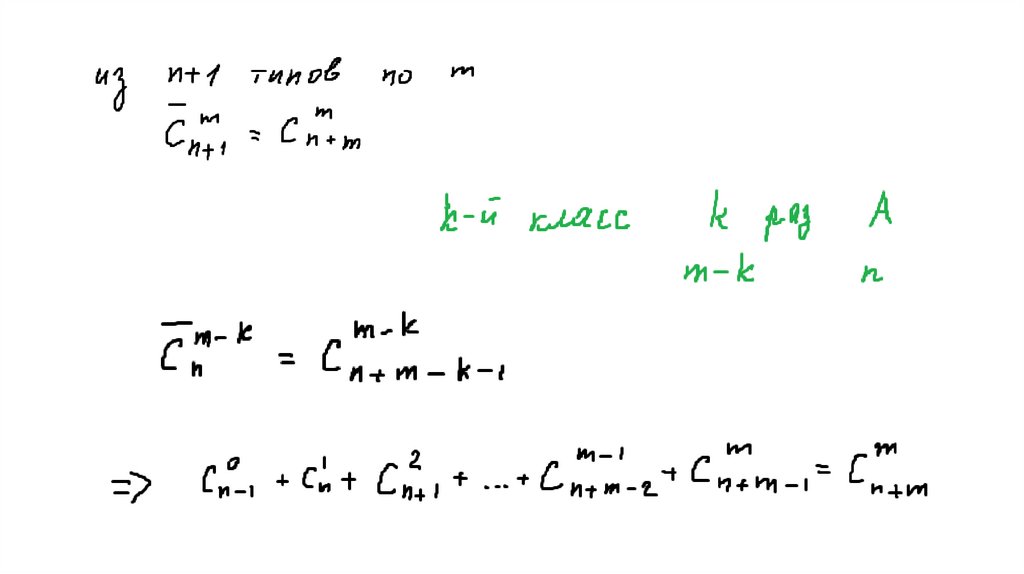
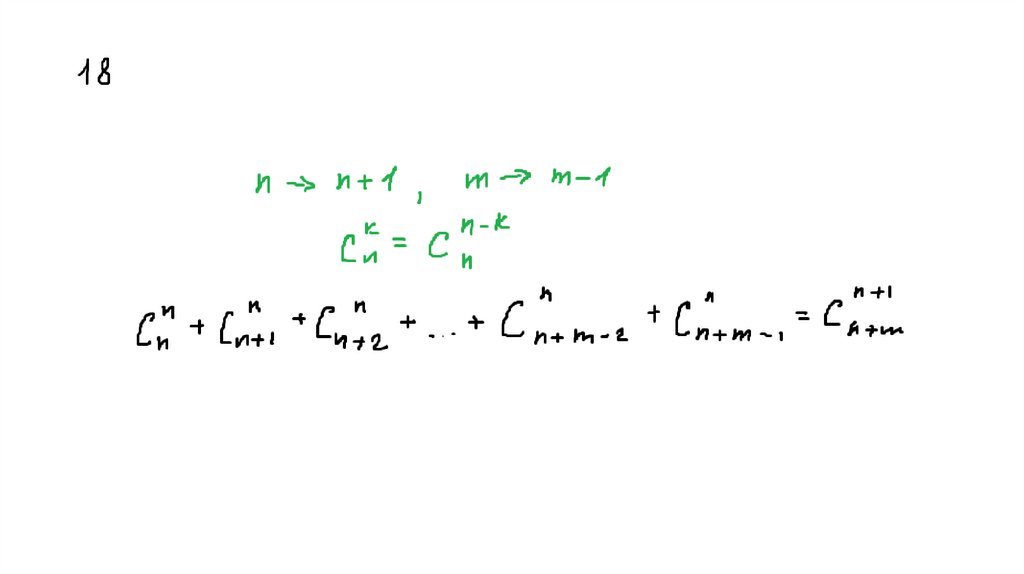

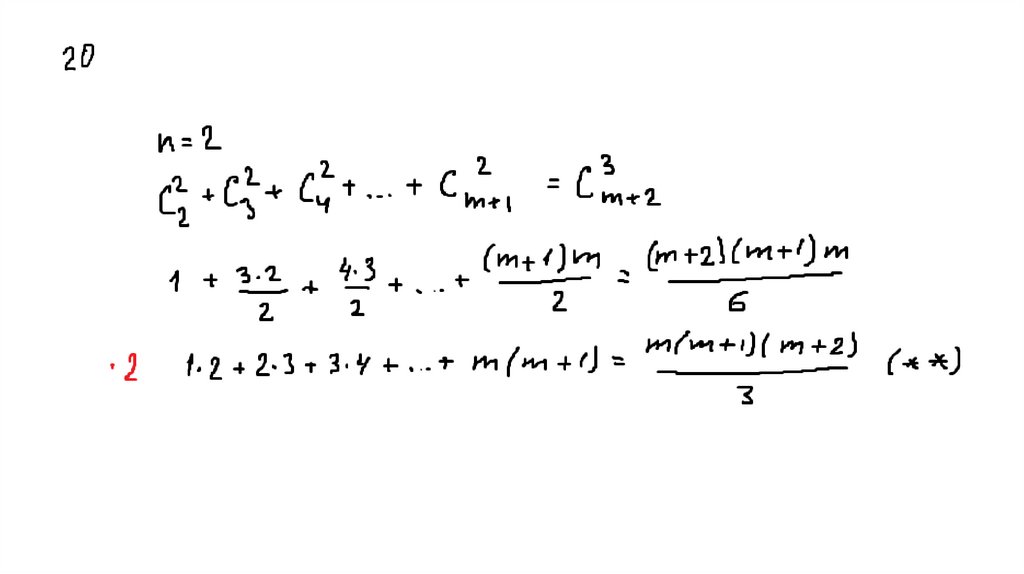
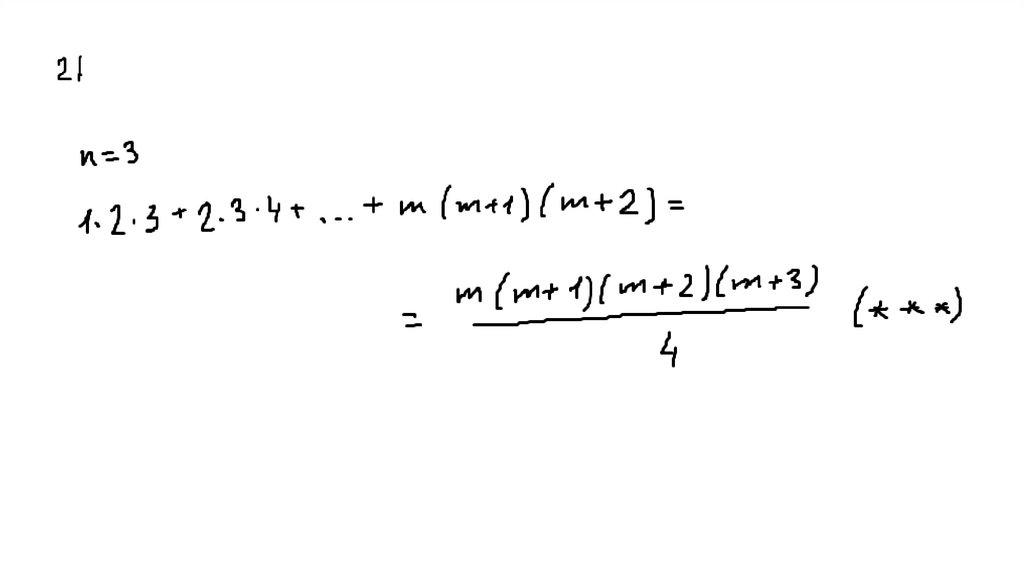

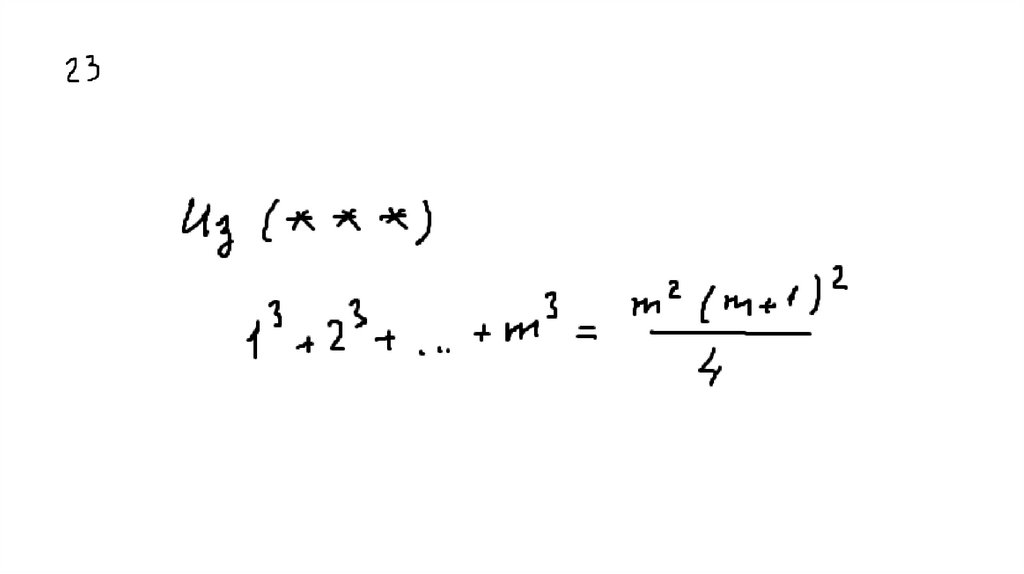
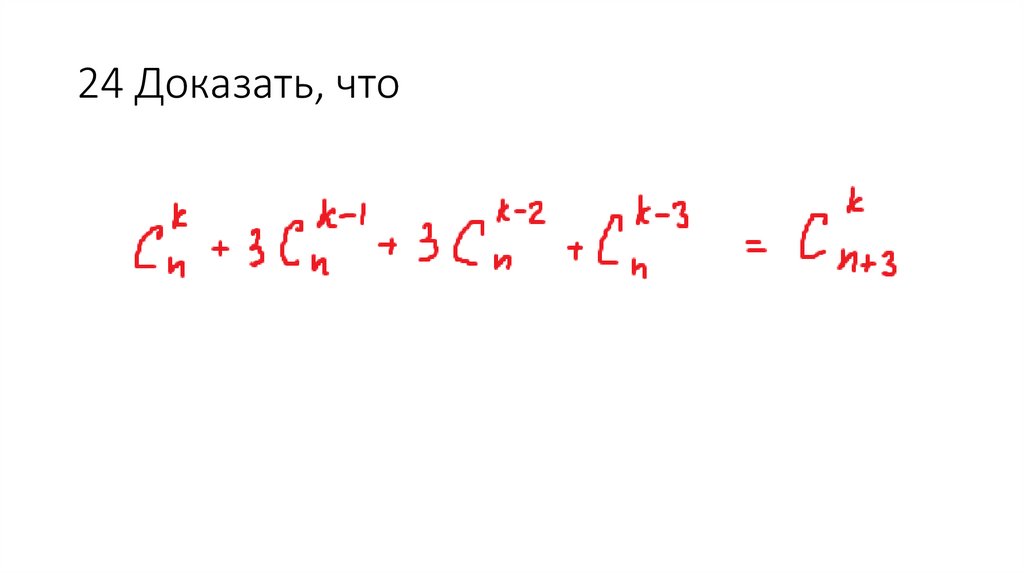




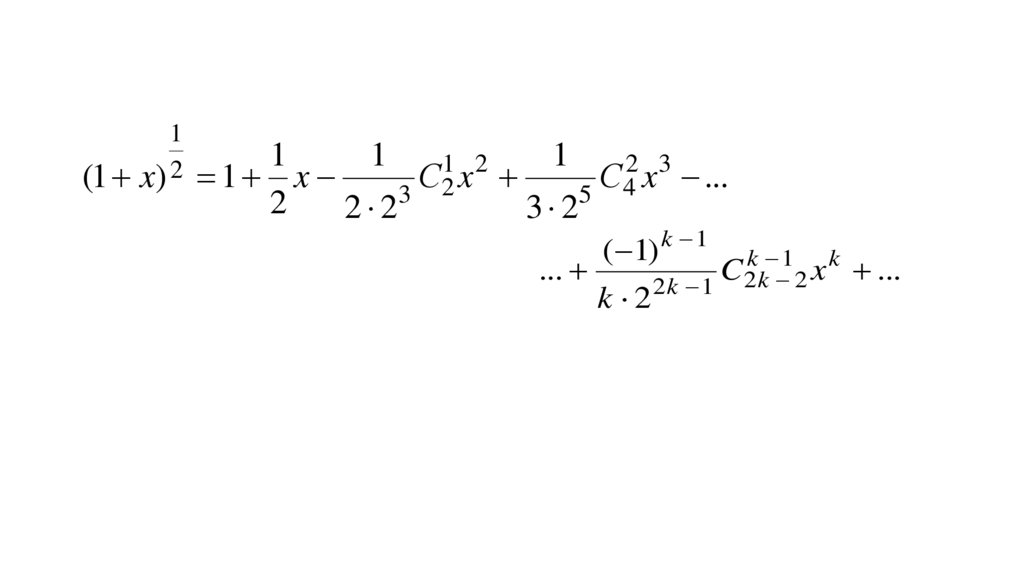
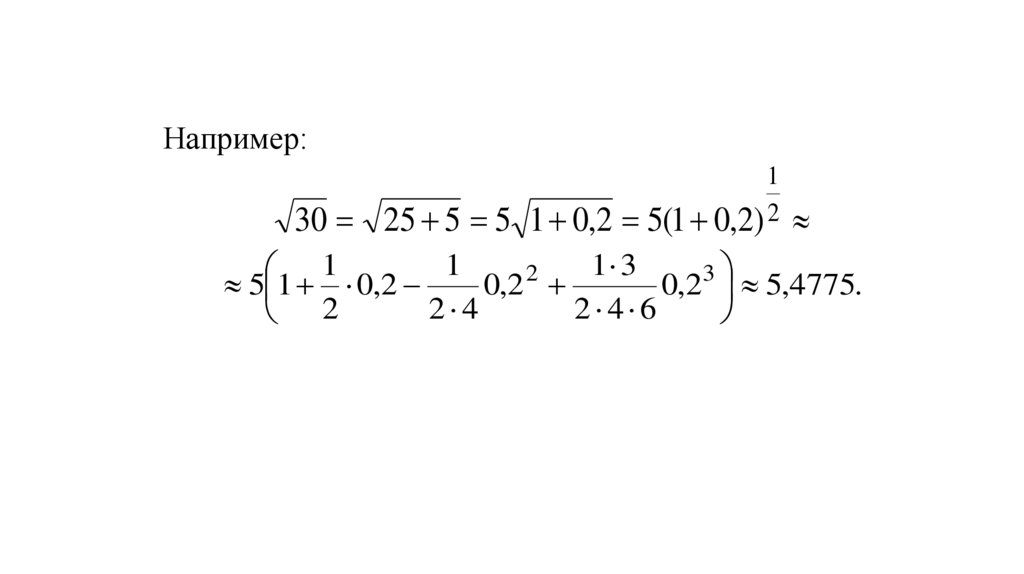

 mathematics
mathematics








