Similar presentations:
Формула бинома Ньютона. Биномиальная формула Ньютона
1.
Урок 112.
• Устно• Заполните пустые квадраты.
• а) (3 + а)2 = + а + а2;
2
2
• б) ( – b) = 49 14 + b ;
2
2
• в) ( + ) = 25 + 10 + ;
• г) (а + )3 = а3 + а + + 27
3.
4.
НЬЮТОН - английский математик,механик, астроном и физик, создатель
классической механики. Разработал
дифференциальное и интегральное
исчисления. Открыл дисперсию света,
исследовал интерференцию и
дифракцию, развивал корпускулярную
теорию света. Построил зеркальный
телескоп. Сформулировал основные
законы классической механики. Открыл
закон всемирного тяготения, создал
теорию движения небесных тел, создав
основы небесной механики.
1643-1727 г.г.
5. В теории многочленов часто двучлены называют биномами.
6. Биномиальная формула Ньютона.
1 n 1n
2 n 2 2
n
(a b) a C a b C a b ...
n
k n k k
n
n
C a b ... b
n
7.
Биномиальные коэффициенты легко находитьс помощью треугольника Паскаля
1
1
1
1
1
1
1
1
7
2
3
4
5
6
1
3
6
10
15
21
1
4
10
20
35
1
1
5
15
35
1
6
21
1
7
1
8.
1623-1662 г.г.ПАСКАЛЬ -французский
математик, физик,
религиозный философ и
писатель. Работы по
арифметике, теории
чисел, алгебре,
геометрии, теории
вероятностей. В 1641г.
сконструировал
суммирующую машину.
9.
Число слагаемых на 1 больше степенибинома.
Коэффициенты находятся по треугольнику
Паскаля.
Коэффициенты симметричны.
Если в скобке знак минус, то знаки + и –
чередуются.
Сумма степеней каждого слагаемого равна
степени бинома.
10. Записать разложение бинома:
11. Определение:
• Для любого натурального числа n (n≥2)справедлива формула:
а b a b a a b a b ... b
n
n
n 1
n 2
n 3 2
n 1
12. Определение:
• Если нечётно, то для любых чисел иливыражений и верно тождество
a b a b a a b a
n
n
Пример:
n
n 1
n 2 2
b ... ab
n 1
b
n
13. Домашнее задание
№ 2.14 в
№ 2.17 б
№ 2.18 в
№ 2.20 в


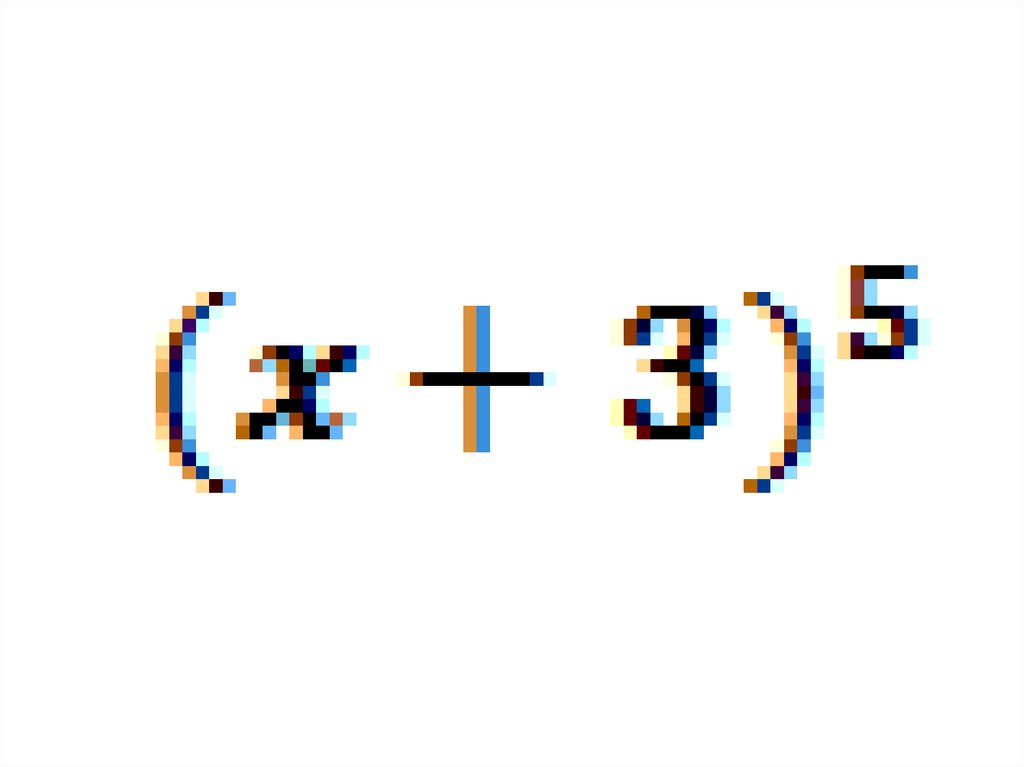










 mathematics
mathematics








