Similar presentations:
Методы определения силовых факторов в деформируемых системах. Лекция 3
1. ЛЕКЦИЯ 3
МЕТОДЫ ОПРЕДЕЛЕНИЯСИЛОВЫХ ФАКТОРОВ
В ДЕФОРМИРУЕМЫХ
СИСТЕМАХ
2.
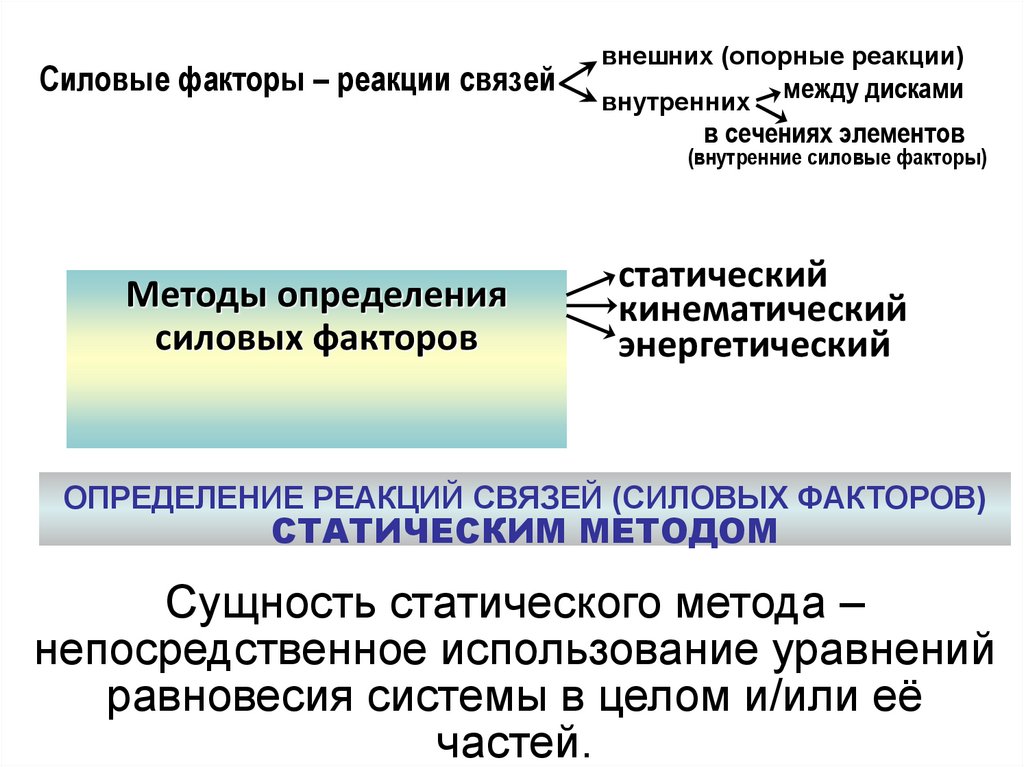
Силовые факторы – реакции связейвнешних (опорные реакции)
внутренних
между дисками
в сечениях элементов
(внутренние силовые факторы)
Методы определения
силовых факторов
статический
кинематический
энергетический
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
Сущность статического метода –
непосредственное использование уравнений
равновесия системы в целом и/или её
частей.
3.
qF2
F1
F1
B
C
C
M
h
A
A
l
l/2
l/2
VA
F 0
F 0
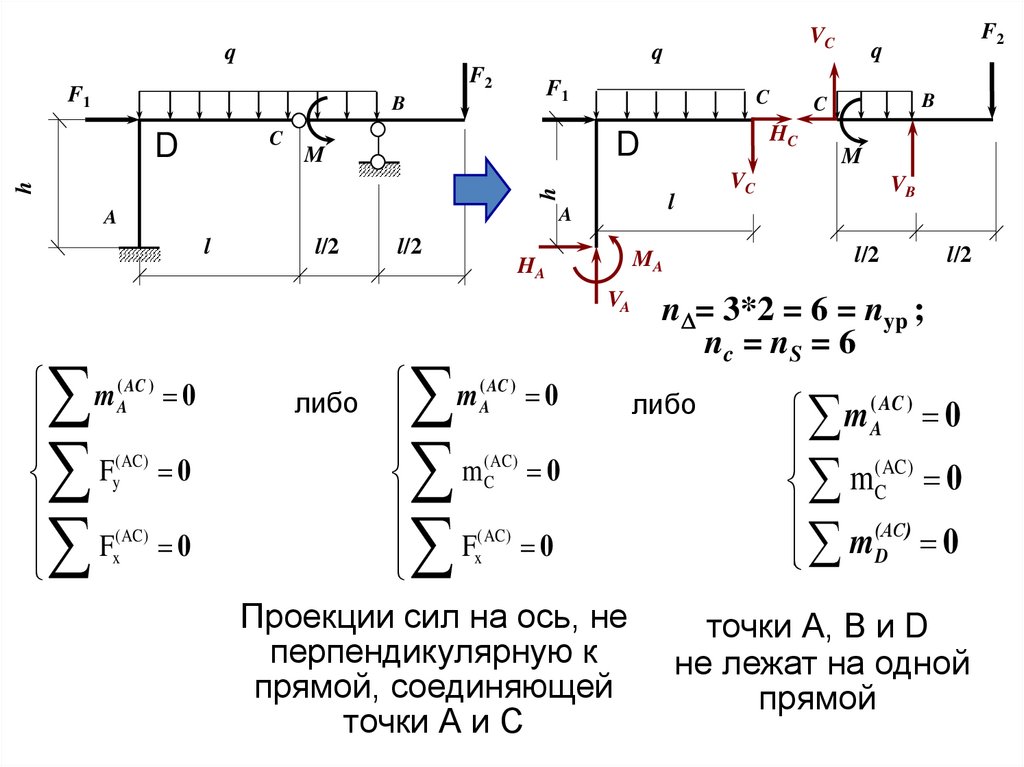
m (AAC ) 0
( AC )
y
( AC )
x
либо
m 0
F 0
m (AAC ) 0
( AC )
C
( AC )
x
Проекции сил на ось, не
перпендикулярную к
прямой, соединяющей
точки А и С
M
VB
l/2
MA
HA
B
VC
l
F2
q
C
HC
D
h
D
VC
q
l/2
nD= 3*2 = 6 = nyp ;
nc = nS = 6
либо
m (AAC ) 0
(AC)
m
C 0
(АC)
m
D 0
точки А, В и D
не лежат на одной
прямой
4.
qF2
F1
F1
B
M
h
l
A
A
C
l/2
l/2
m (AAC ) 0
F y(AC) 0
(AC)
F
0
x
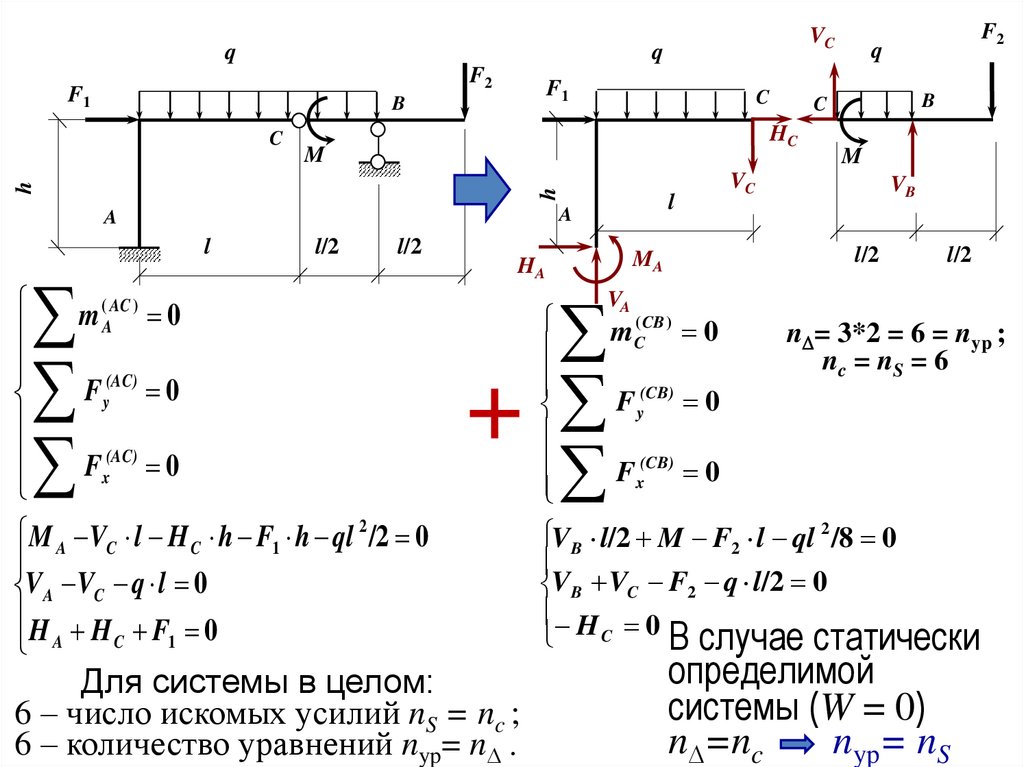
M A VC l H C h F1 h ql 2 /2 0
V A VC q l 0
H H F 0
C
1
A
MA
HA
F2
q
B
C
HC
h
C
l
VC
q
M
VC
VB
l/2
l/2
+
Для системы в целом:
6 – число искомых усилий nS = nc ;
6 – количество уравнений nyp= nD .
VA
mC( CB ) 0
nD= 3*2 = 6 = nyp ;
nc = nS = 6
F y(CB) 0
(CB)
F
0
x
VB l/2 M F2 l ql 2 /8 0
VB VC F2 q l/2 0
H 0
C
В случае статически
определимой
cистемы (W = 0)
nD=nc
nyp= nS
5. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ) КИНЕМАТИЧЕСКИМ МЕТОДОМ
В основе метода – принцип возможных перемещений (принцип Лагранжа )*:
если механическая система находится в равновесии,
то сумма работ внешних сил, приложенных к системе,
и соответствующих им внутренних сил
на возможных ( виртуальных) перемещениях
равна нулю:
Wext + Wint = 0
*J.L. Lagrange ( 1788 )
6. Возможные (виртуальные) перемещения –
а) бесконечно малые ( для линейнодеформируемых систем – конечные,
но малые в сравнении с габаритами
системы );
б) не противоречащие условиям
совместности деформаций
( перемещений ) и кинематическим
граничным условиям ( условиям
закрепления );
в) отсчитываемые от исследуемого
положения равновесия.
7.
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
Силовой фактор S в линейно деформируемой системе
определяется как производная потенциальной энергии
упругой деформации U (ПЭУД) по соответствующему
перемещению DS по направлению S
( т е о р е м а Л а г р а н ж а ):
S dU
dΔ S
8.
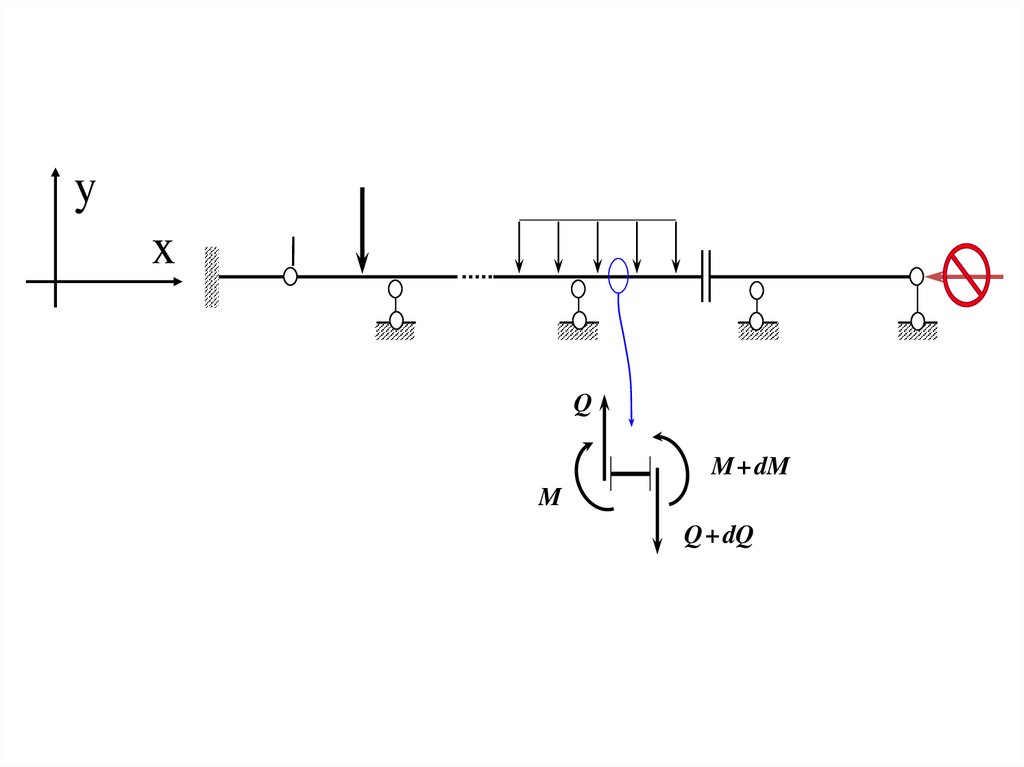
Qy
q
x
M dM
M
dx
Q dQ
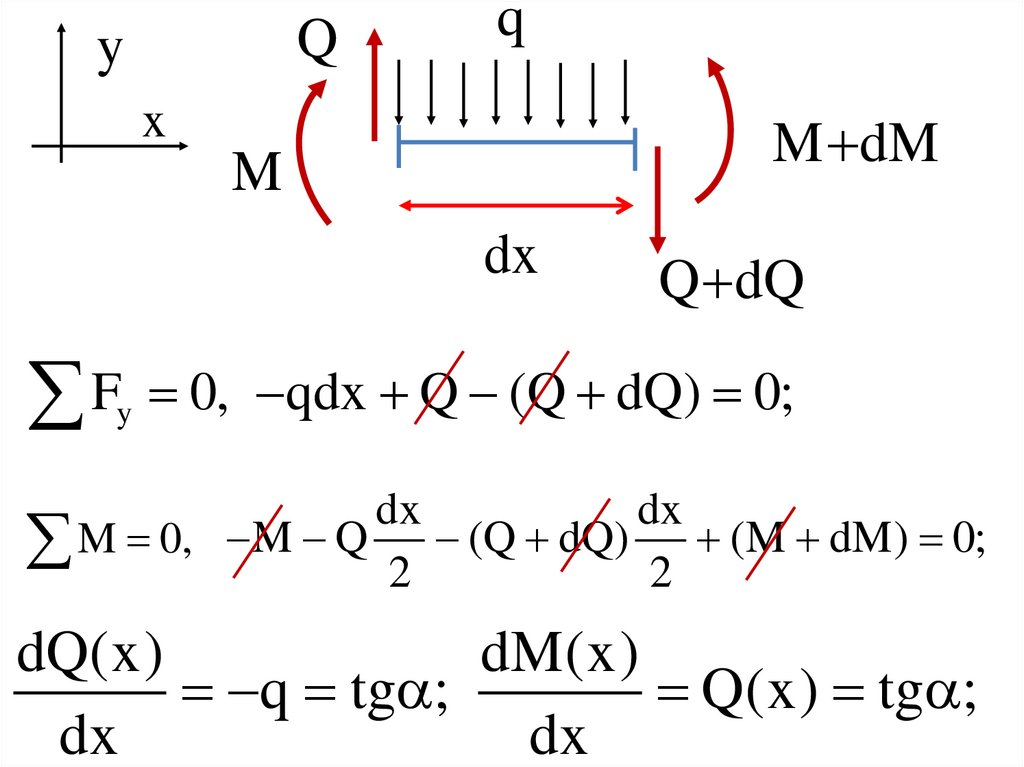
F 0, qdx Q (Q dQ) 0;
y
dx
dx
M 0, M Q 2 (Q dQ) 2 (M dM) 0;
dQ(x)
dM(x)
q tg ;
Q(x) tg ;
dx
dx
9.
2d M(x)
q(x);
2
dx
10.
Конец лекции11.
F1q
Fn
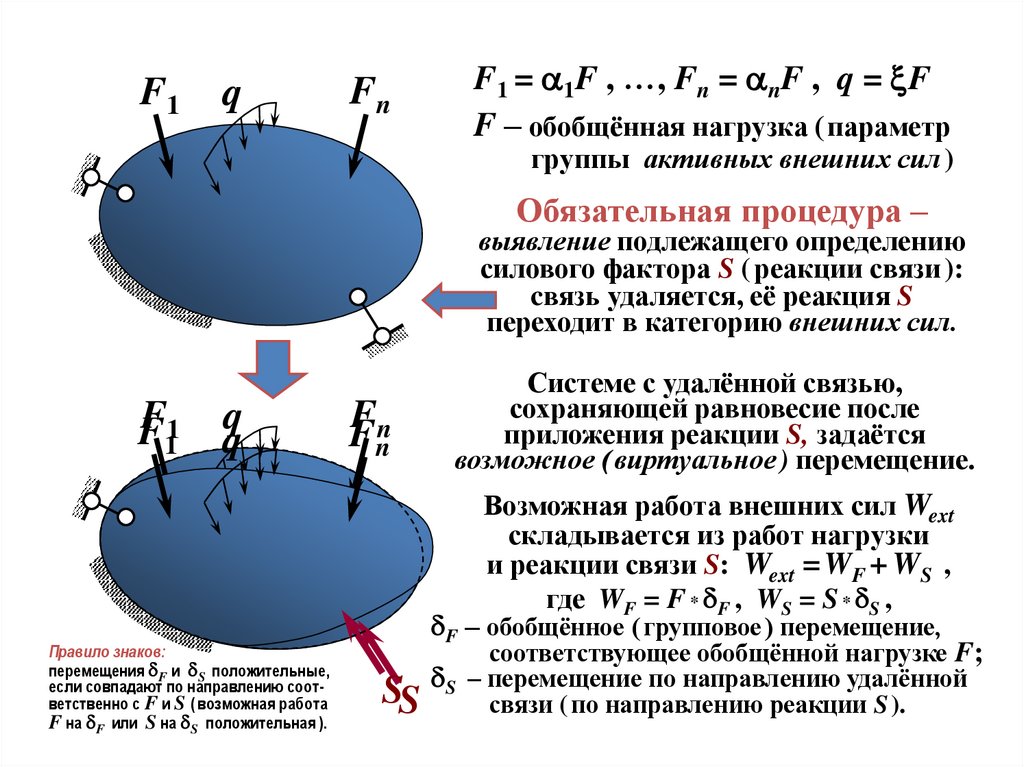
F1 = 1F , …, Fn = nF , q = xF
F – обобщённая нагрузка ( параметр
группы активных внешних сил )
Обязательная процедура –
выявление подлежащего определению
силового фактора S ( реакции связи ):
cвязь удаляется, её реакция S
переходит в категорию внешних сил.
F1
F
1
q
q
Fn
F
n
Системе с удалённой связью,
сохраняющей равновесие после
приложения реакции S, задаётся
возможное ( виртуальное ) перемещение.
Возможная работа внешних сил Wext
складывается из работ нагрузки
и реакции связи S: Wext = WF + WS ,
где WF = F * dF , WS = S * dS ,
Правило знаков:
перемещения dF и dS положительные,
если совпадают по направлению соответственно с F и S ( возможная работа
F на dF или S на dS положительная ).
dF – обобщённое ( групповое ) перемещение,
соответствующее обобщённой нагрузке F;
по направлению удалённой
SS dS – перемещение
связи ( по направлению реакции S ).
12. Алгоритм определения реакции связи кинематическим методом
1. В системе, находящейся в равновесном деформированномсостоянии при заданной нагрузке, удаляется связь, реакцию
которой S требуется определить. Взамен удалённой связи
прикладывается её реакция S, обеспечивающая сохранение
неизменным состояния равновесия системы.
2. Системе с удалённой связью, находящейся по-прежнему
в равновесном деформированном состоянии при действующей
нагрузке и реакции S, задаётся возможное (виртуальное)
перемещение.
3. Определяются (с точностью до общего неопределённого
множителя d0 ) перемещения dF и dS – соответственно
по направлениям заданной нагрузки F и искомой реакции S.
4. Из уравнения возможных работ Wext + Wint = 0 определяется
искомый силовой фактор S (реакция связи):
F δF Wint
S
δS
13.
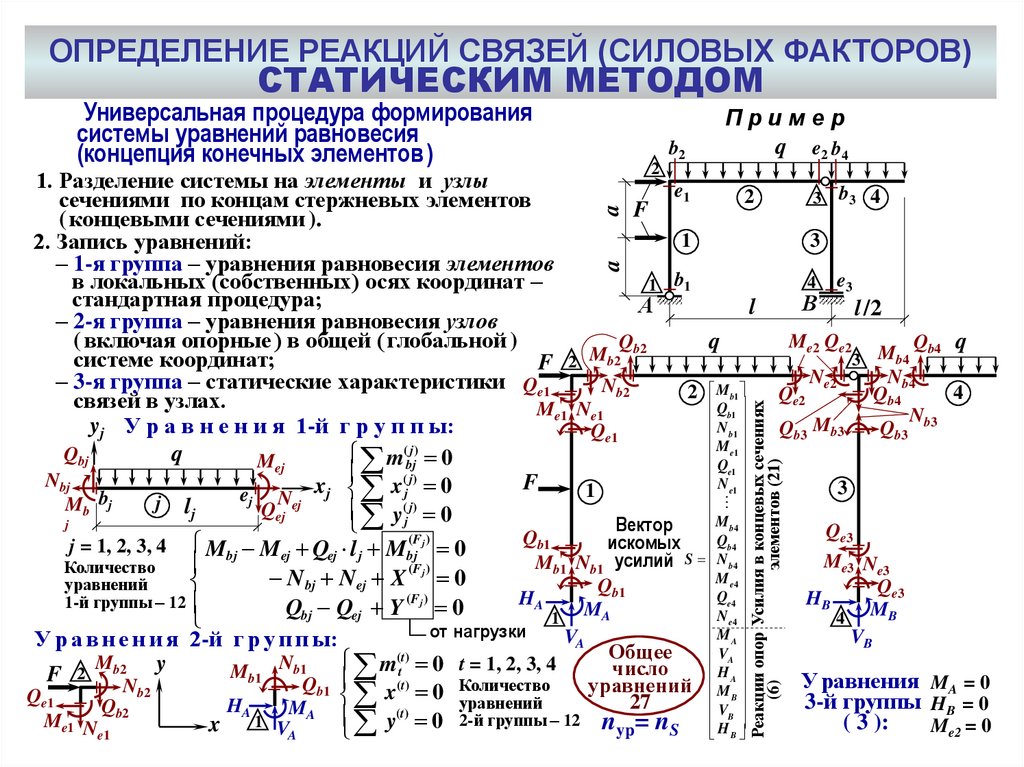
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)СТАТИЧЕСКИМ МЕТОДОМ
Универсальная процедура формирования
системы уравнений равновесия
(концепция конечных элементов )
b2
Пример
q e2 b 4
2
Реакции опор Усилия в концевых сечениях
(6)
элементов (21)
a
a
1. Разделение системы на элементы и узлы
e1
2
3 b3 4
сечениями по концам стержневых элементов
F
( концевыми сечениями ).
1
3
2. Запись уравнений:
– 1-я группа – уравнения равновесия элементов
4 e3
в локальных (собственных) осях координат –
1 b1
стандартная процедура;
В
А
l
l /2
– 2-я группа – уравнения равновесия узлов
( включая опорные ) в общей ( глобальной )
Me2 Qe2
q
Q q
Qb2
Mb4 b4
M
b2
3
системе координат;
2
F
Ne2
Nb4
– 3-я группа – статические характеристики Qe1
Nb2
M b1
2
4
Q
Q
b4
e2
связей в узлах.
Qb1
Me1 Ne1
N
N
yj У р а в н е н и я 1-й г р у п п ы:
Qb3 b3
Qb3 Mb3
Qe1
b1
M e1
Qbj
q
m(bjj) 0
Mej
Qe1
( j)
N e1
Nbj
F
xj x j 0
3
1
e
N
b
j
ej
j lj
Mb j
(
j
)
Qej
yj 0
j
Вектор
M b4
Qe3
Qb1
искомых Qb4
j = 1, 2, 3, 4 Mbj Mej Qej l j Mbj(F j ) 0
Me3 Ne3
Mb1 Nb1 усилий S N b4
Количество
(F j )
M
N
N
X
0
bj
ej
уравнений
e4
Qb1
Qe3
(F j )
HA
HB
Qe4
1-й группы – 12
Qbj Qej Y 0
MB
N e4
1 MA
4
от нагрузки
M
VA
VB
У р а в н е н и я 2-й г р у п п ы:
V A
Общее
A
m(tt) 0 t = 1, 2, 3, 4
M
число
Mb1 Nb1
F 2 b2N y
HA
У равнения MA = 0
(
t
)
Q
Количество
уравнений
b1
MB
b2
x 0 уравнений
Qe1
27
3-й группы HB = 0
HA
VB
Q
MA
(t )
2-й
группы
–
12
1
Me1 N b2
y
0
( 3 ):
nyp= nS H B
x
Me2 = 0
VA
e1
14.
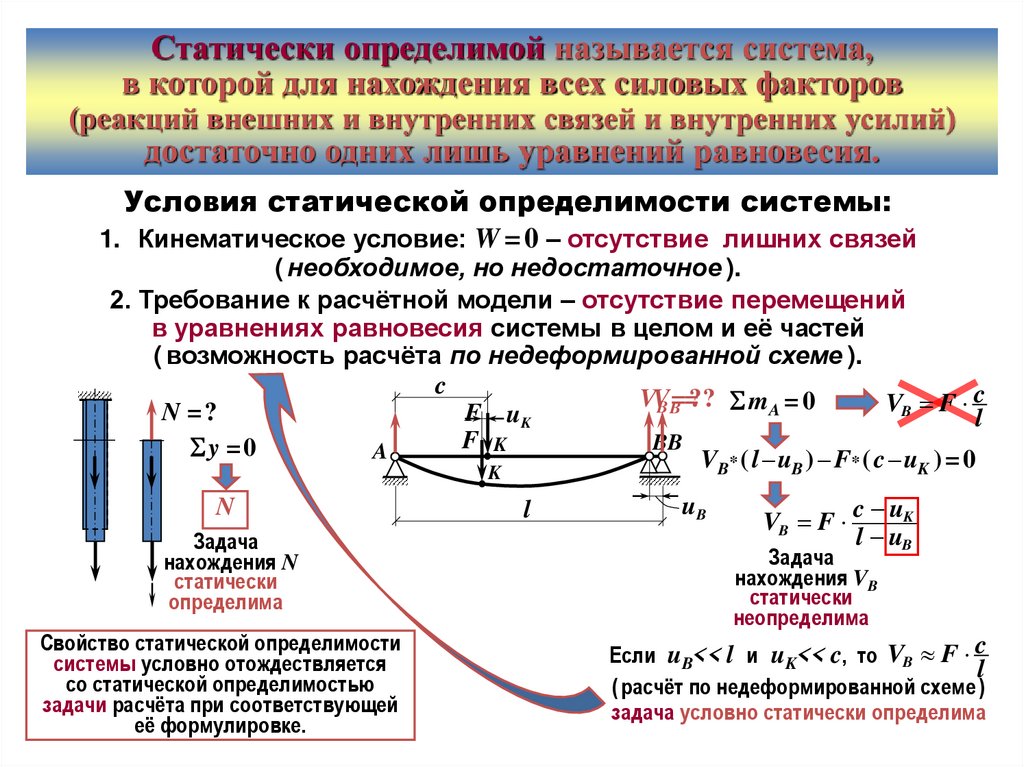
Статически определимой называется система,в которой для нахождения всех силовых факторов
(реакций внешних и внутренних связей и внутренних усилий)
достаточно одних лишь уравнений равновесия.
Условия статической определимости системы:
1. Кинематическое условие: W = 0 – отсутствие лишних связей
( необходимое, но недостаточное ).
2. Требование к расчётной модели – отсутствие перемещений
в уравнениях равновесия системы в целом и её частей
( возможность расчёта по недеформированной схеме ).
c
c
VV
==?? S mA = 0
V
F
B
B
B
N =?
F uK
l
F K
BB
Sy =0
A
V * ( l – u ) – F* ( c – u ) = 0
B
K
N
Задача
нахождения N
статически
определима
Свойство статической определимости
системы условно отождествляется
со статической определимостью
задачи расчёта при соответствующей
её формулировке.
l
uB
B
VB F
K
c uK
l uB
Задача
нахождения VB
статически
неопределима
Если uB<< l и uK<< c, то VB F c
l
( расчёт по недеформированной схеме )
задача условно статически определима
15.
yx
Q
M + dM
M
Q + dQ




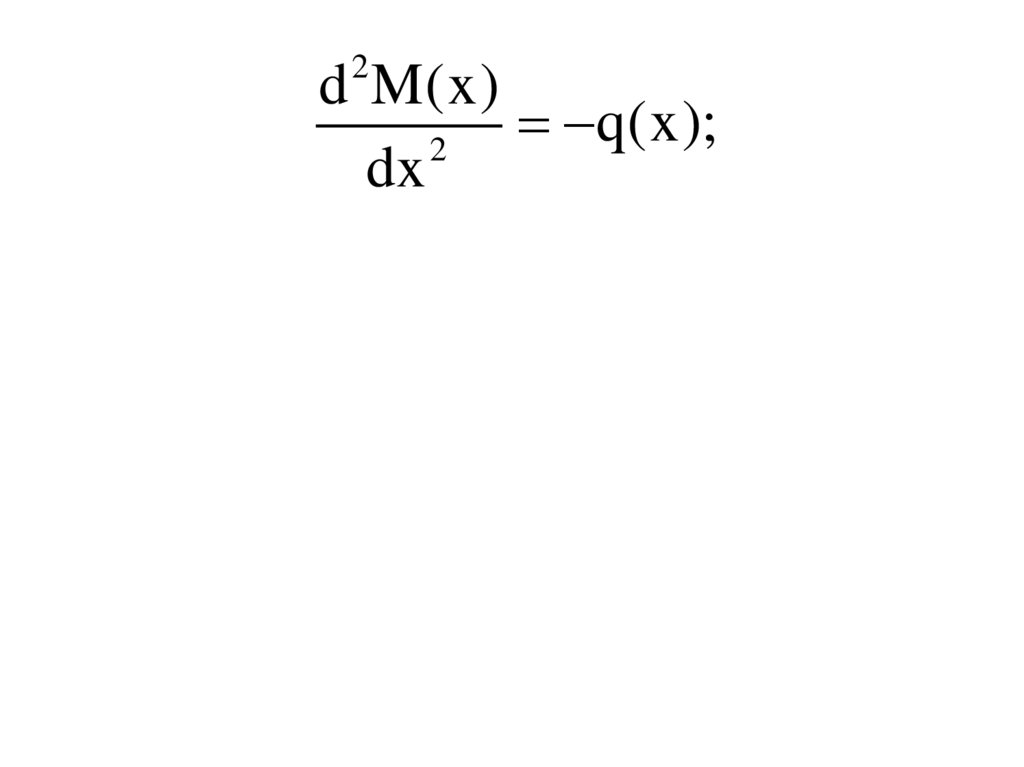


 Construction
Construction








