Настройка контуров и их оптимизация

1. Настройка контуров и их оптимизация

Предварительные рассуждения
Пусть имеется объект регулирования (ОР) с передаточной функцией (п.ф.) WOP(p)
f(p)
g(p)=x*(p)
u(p)
1
WОР(p)
Регулятор
x(p)
WОР(p)
Объект
регулирования
С позиции синтеза системы с
последовательной коррекцией «в большом»
очевидно, что построение идеальной системы
точного воспроизведения требует введения в
САР корректирующего звена (регулятора) с
п.ф., равной обратной п.ф. ОР.
В этом случае имеет место точная компенсация передаточной функции ОР, а
результирующая передаточная функция разомкнутой САР будет равна:
W p
x(t)
t
1
WOP p
WOP p 1
Переходной функцией системы будет скачкообразная
функция. С т.з. качества САР такое поведение x(t) является
идеальным – имеет место максимально возможное
быстродействие при полном отсутствии
перерегулирования.
Даже если предположить, что точное математическое описание ОР известно, и
регулятор с указанной передаточной функции реализован, система будет отличаться от
идеальной ввиду действия на ОР возмущений.

2.

Настройка контуров и их оптимизация
Предварительные рассуждения
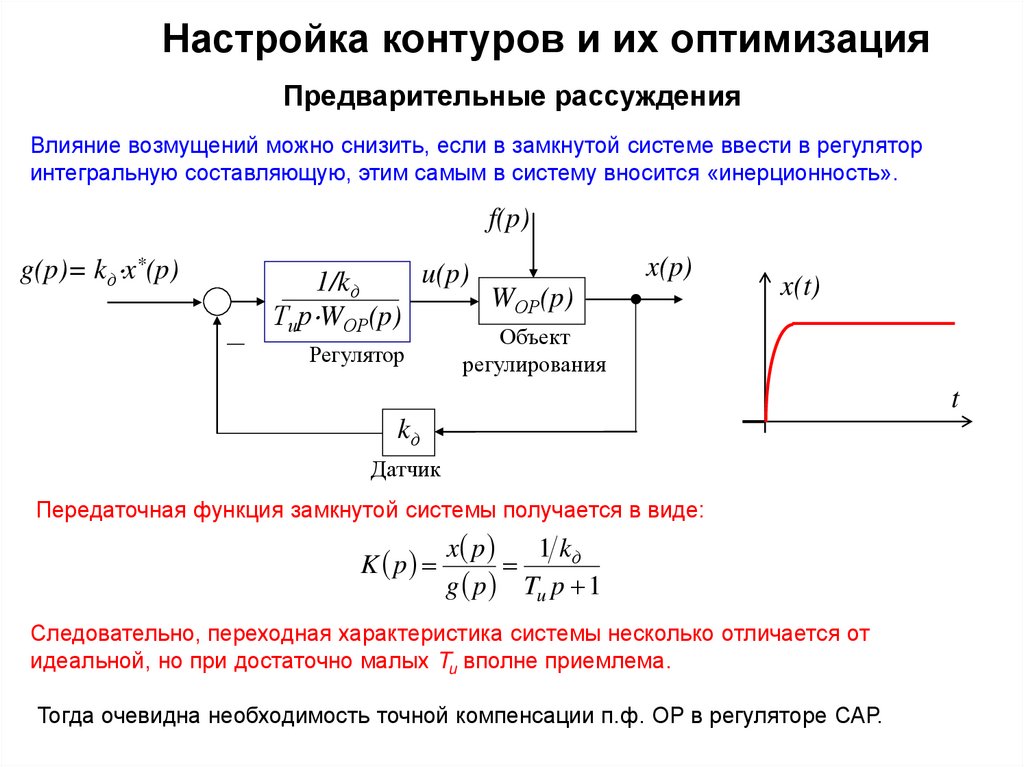
Влияние возмущений можно снизить, если в замкнутой системе ввести в регулятор
интегральную составляющую, этим самым в систему вносится «инерционность».
f(p)
g(p)= kд x*(p)
u(p)
1/kд
WОР(p)
Тир WОР(p)
Регулятор
x(p)
x(t)
Объект
регулирования
t
kд
Датчик
Передаточная функция замкнутой системы получается в виде:
K p
x p
1 kд
g p Tu p 1
Следовательно, переходная характеристика системы несколько отличается от
идеальной, но при достаточно малых Tu вполне приемлема.
Тогда очевидна необходимость точной компенсации п.ф. ОР в регуляторе САР.

3.

Настройка контуров и их оптимизация
Предварительные рассуждения
f(p)
g(p)= kд x*(p)
u(p)
1/kд
WОР(p)
Тир WОР(p)
Регулятор
x(p)
x(t)
Объект
регулирования
t
kд
Датчик
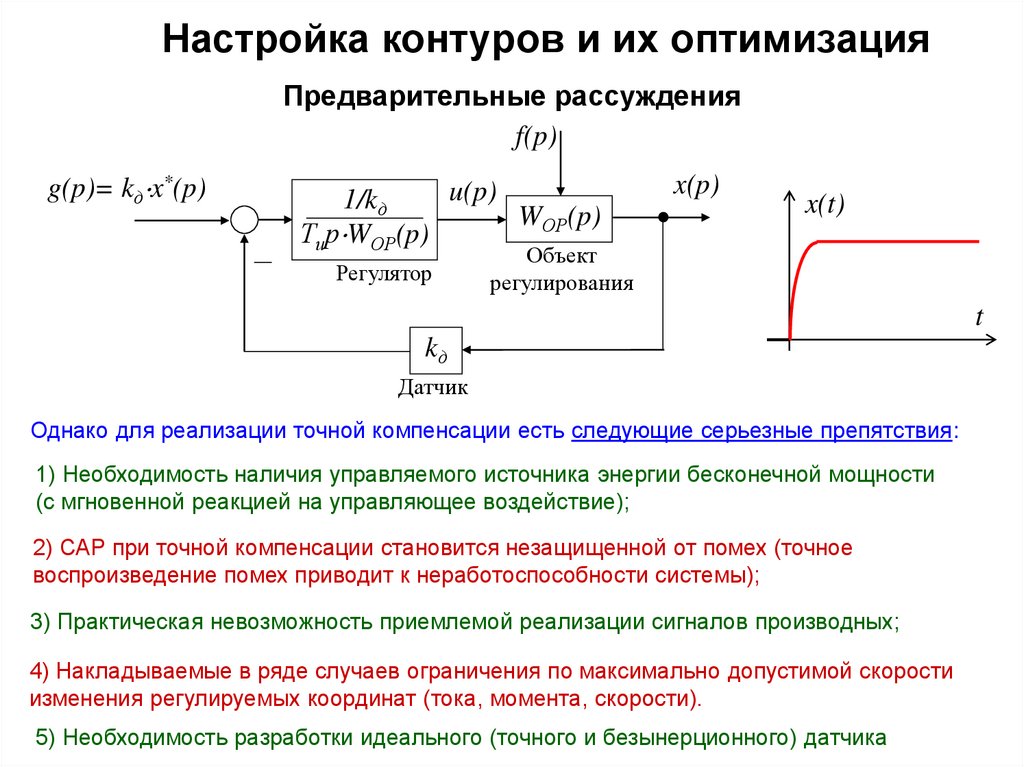
Однако для реализации точной компенсации есть следующие серьезные препятствия:
1) Необходимость наличия управляемого источника энергии бесконечной мощности
(с мгновенной реакцией на управляющее воздействие);
2) САР при точной компенсации становится незащищенной от помех (точное
воспроизведение помех приводит к неработоспособности системы);
3) Практическая невозможность приемлемой реализации сигналов производных;
4) Накладываемые в ряде случаев ограничения по максимально допустимой скорости
изменения регулируемых координат (тока, момента, скорости).
5) Необходимость разработки идеального (точного и безынерционного) датчика

4.

Настройка контуров и их оптимизация
Предварительные рассуждения
f(p)
g(p)= kд x*(p)
u(p)
1/kд
WОР(p)
Тир WОР(p)
Регулятор
x(p)
x(t)
Объект
регулирования
t
kд
Датчик
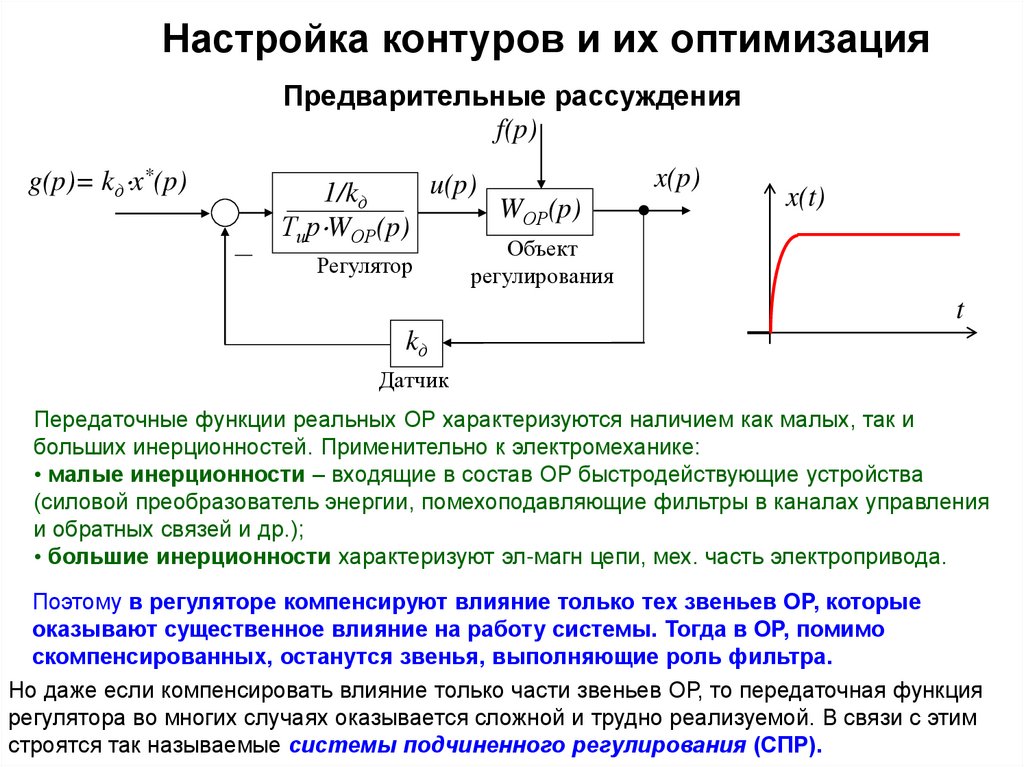
Передаточные функции реальных ОР характеризуются наличием как малых, так и
больших инерционностей. Применительно к электромеханике:
• малые инерционности – входящие в состав ОР быстродействующие устройства
(силовой преобразователь энергии, помехоподавляющие фильтры в каналах управления
и обратных связей и др.);
• большие инерционности характеризуют эл-магн цепи, мех. часть электропривода.
Поэтому в регуляторе компенсируют влияние только тех звеньев ОР, которые
оказывают существенное влияние на работу системы. Тогда в ОР, помимо
скомпенсированных, останутся звенья, выполняющие роль фильтра.
Но даже если компенсировать влияние только части звеньев ОР, то передаточная функция
регулятора во многих случаях оказывается сложной и трудно реализуемой. В связи с этим
строятся так называемые системы подчиненного регулирования (СПР).

5.

Настройка контуров и их оптимизация
Технический оптимум
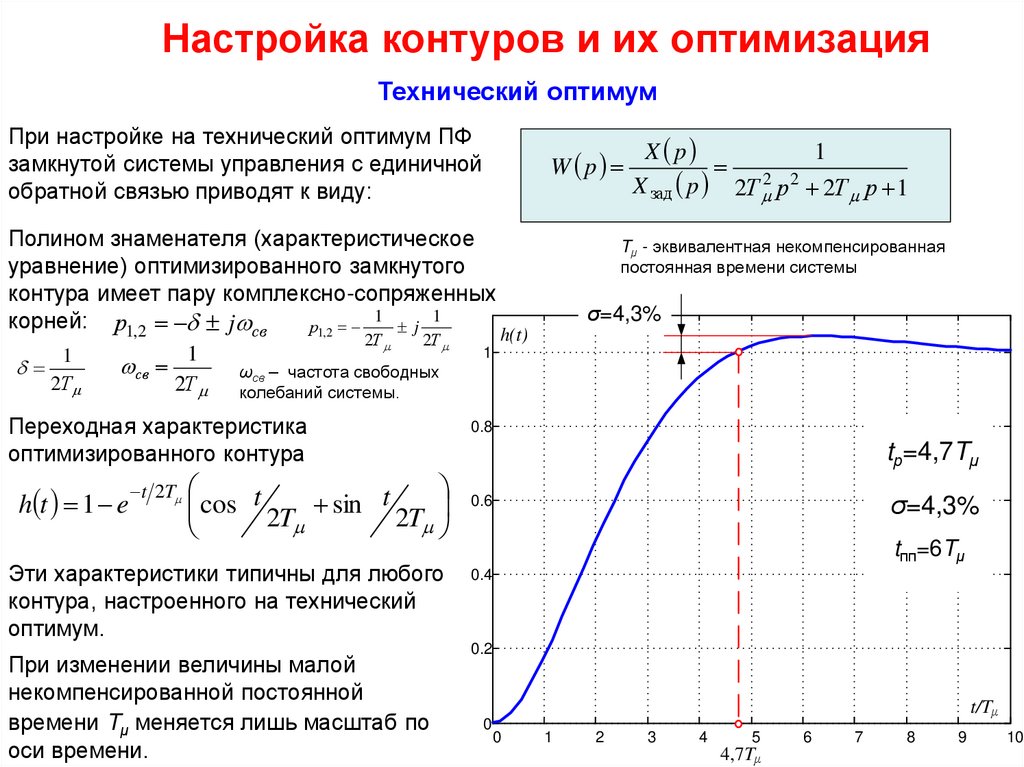
При настройке на технический оптимум ПФ
замкнутой системы управления с единичной
обратной связью приводят к виду:
W p
Полином знаменателя (характеристическое
уравнение) оптимизированного замкнутого
контура имеет пару комплексно-сопряженных
1
1
корней: р1, 2 j св
р1,2
j
h(t)
2Т
2Т
1
1
1
св
ωсв – частота свободных
2Т
2Т колебаний системы.
Переходная характеристика
оптимизированного контура
h t 1 e
t 2T
cos t 2T sin t 2T
Эти характеристики типичны для любого
контура, настроенного на технический
оптимум.
При изменении величины малой
некомпенсированной постоянной
времени Tμ меняется лишь масштаб по
оси времени.
X p
1
2 2
X зад p 2Т р 2Т р 1
Tμ - эквивалентная некомпенсированная
постоянная времени системы
σ=4,3%
0.8
tр=4,7Tμ
σ=4,3%
0.6
tпп=6Tμ
0.4
0.2
0
t/Tμ
0
1
2
3
4
5
4,7Tμ
6
7
8
9
10

6.

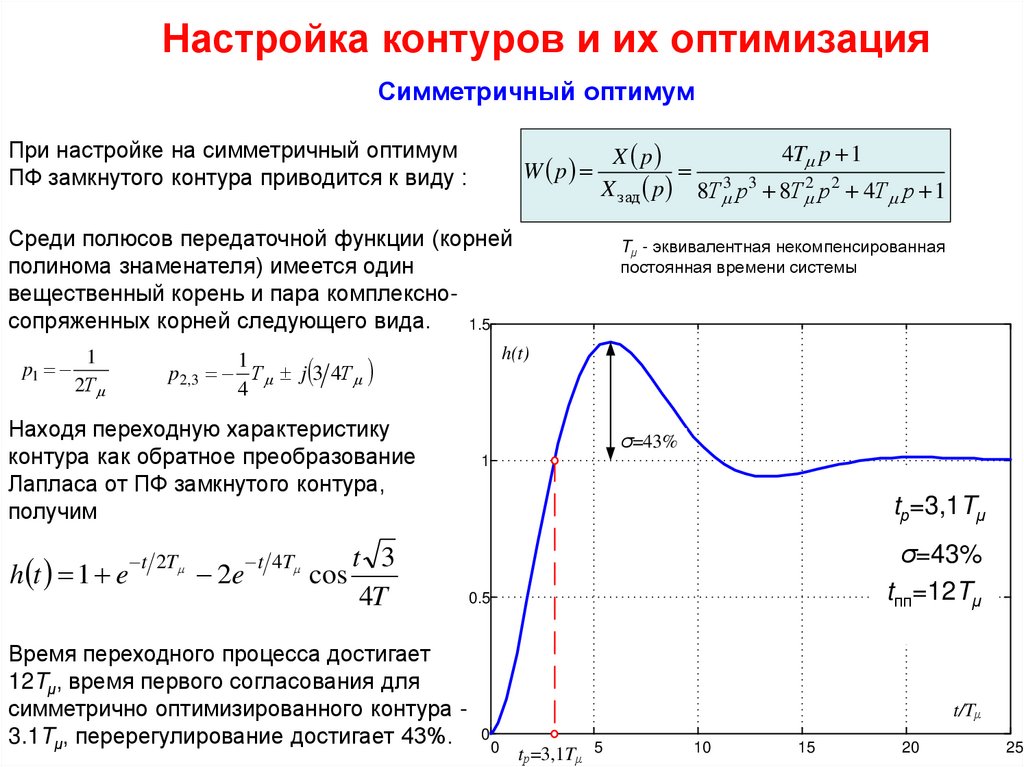
Настройка контуров и их оптимизация
Симметричный оптимум
При настройке на симметричный оптимум
ПФ замкнутого контура приводится к виду :
W p
4T p 1
X p
3 3
X зад p 8Т р 8Т 2 р 2 4Т р 1
Среди полюсов передаточной функции (корней
полинома знаменателя) имеется один
вещественный корень и пара комплексносопряженных корней следующего вида.
1.5
p1
1
2Т
1
p2,3 Т j 3 4Т
4
Находя переходную характеристику
контура как обратное преобразование
Лапласа от ПФ замкнутого контура,
получим
h t 1 e
t 2T
2e
t 4T
t 3
cos
4T
Tμ - эквивалентная некомпенсированная
постоянная времени системы
h(t)
σ=43%
1
tр=3,1Tμ
σ=43%
tпп=12Tμ
0.5
Время переходного процесса достигает
12Tμ, время первого согласования для
симметрично оптимизированного контура 3.1Tμ, перерегулирование достигает 43%. 0 0
t/Tμ
tр=3,1Tμ 5
10
15
20
25

7.

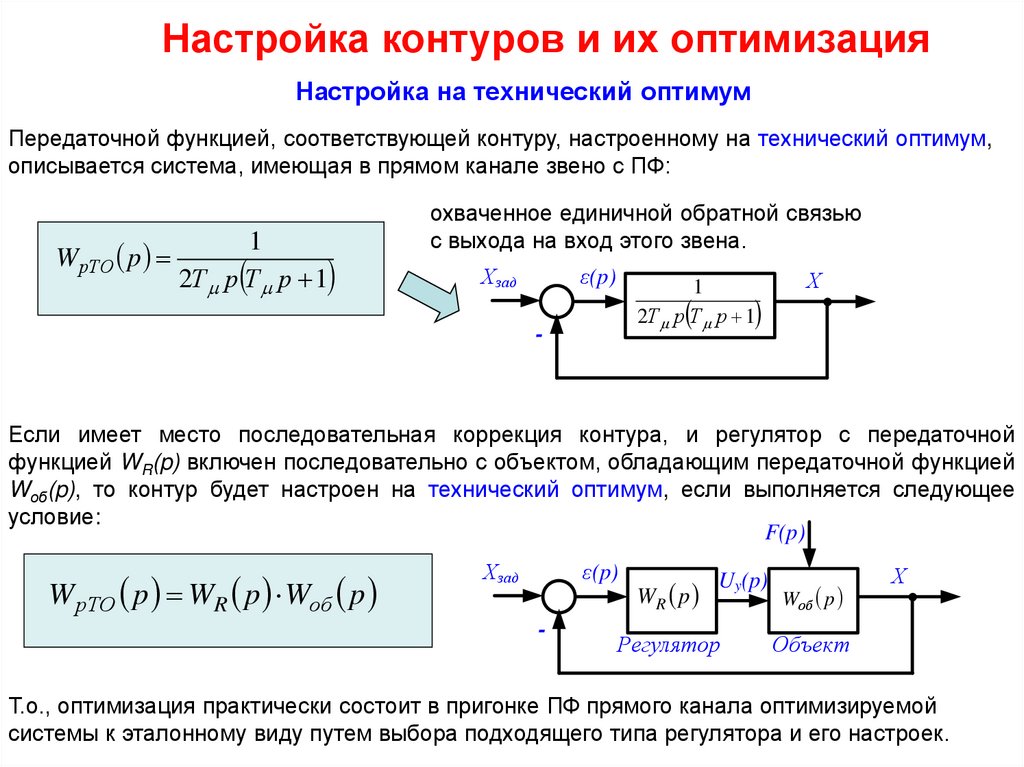
Настройка контуров и их оптимизация
Настройка на технический оптимум
Передаточной функцией, соответствующей контуру, настроенному на технический оптимум,
описывается система, имеющая в прямом канале звено с ПФ:
WрТО p
1
2Т р Т р 1
охваченное единичной обратной связью
с выхода на вход этого звена.
Хзад
ε(p)
1
2Т р Т р 1
-
Х
Если имеет место последовательная коррекция контура, и регулятор с передаточной
функцией WR(p) включен последовательно с объектом, обладающим передаточной функцией
Wоб(p), то контур будет настроен на технический оптимум, если выполняется следующее
условие:
F(p)
W рТО p WR p Wоб p
Хзад
ε(p)
-
WR p
Uy(p)
Регулятор
Wоб p
Х
Объект
Т.о., оптимизация практически состоит в пригонке ПФ прямого канала оптимизируемой
системы к эталонному виду путем выбора подходящего типа регулятора и его настроек.

8.

1
Настройка контуров и их оптимизация
Настройка на технический оптимум
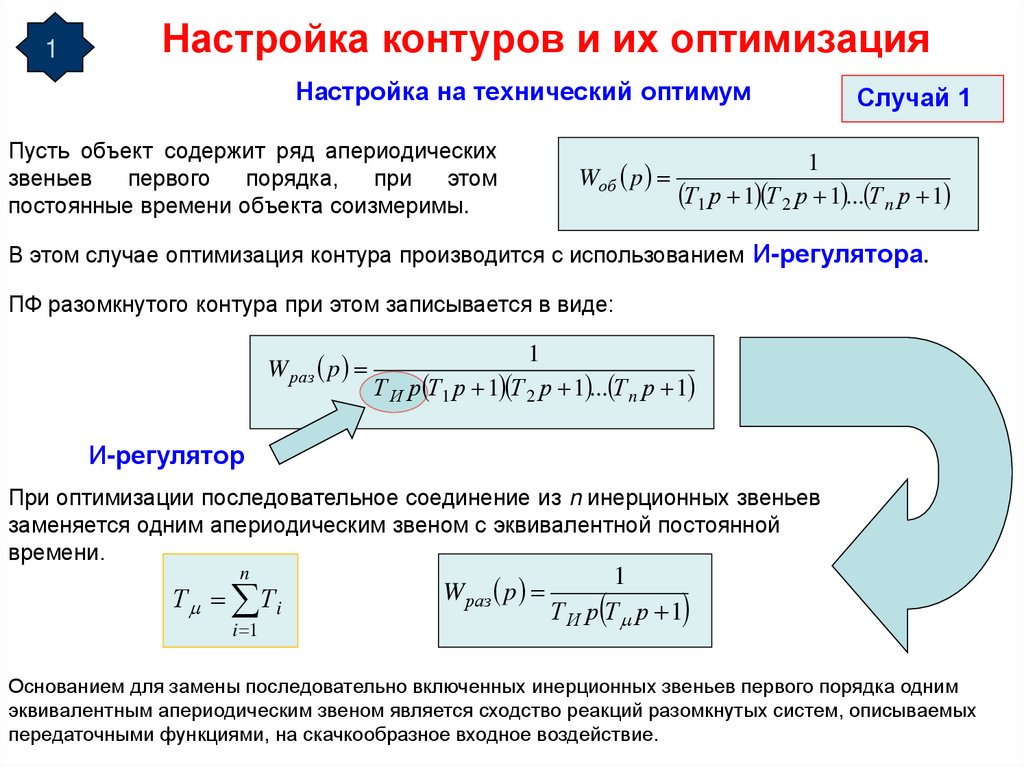
Пусть объект содержит ряд апериодических
звеньев
первого
порядка,
при
этом
постоянные времени объекта соизмеримы.
Wоб p
Случай 1
1
Т1 р 1 Т 2 р 1 ... Т n р 1
В этом случае оптимизация контура производится с использованием И-регулятора.
ПФ разомкнутого контура при этом записывается в виде:
W раз p
1
Т И р Т1 р 1 Т 2 р 1 ... Т n р 1
И-регулятор
При оптимизации последовательное соединение из n инерционных звеньев
заменяется одним апериодическим звеном с эквивалентной постоянной
времени.
n
Т Т i
i 1
Wраз p
1
ТИ р Т р 1
Основанием для замены последовательно включенных инерционных звеньев первого порядка одним
эквивалентным апериодическим звеном является сходство реакций разомкнутых систем, описываемых
передаточными функциями, на скачкообразное входное воздействие.

9.

1
Настройка контуров и их оптимизация
Настройка на технический оптимум
Случай 1
10
9
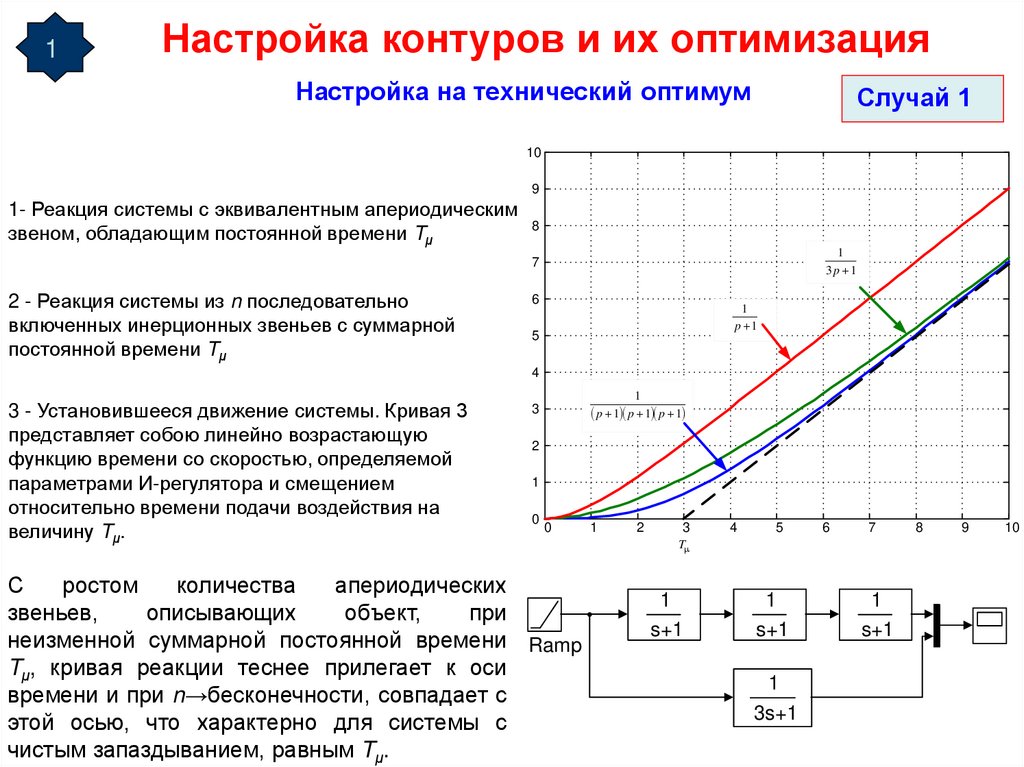
1- Реакция системы с эквивалентным апериодическим
8
звеном, обладающим постоянной времени Tμ
1
3p 1
7
2 - Реакция системы из n последовательно
включенных инерционных звеньев с суммарной
постоянной времени Tμ
6
1
p 1
5
4
3 - Установившееся движение системы. Кривая 3
представляет собою линейно возрастающую
функцию времени со скоростью, определяемой
параметрами И-регулятора и смещением
относительно времени подачи воздействия на
величину Tμ.
1
p 1 p 1 p 1
3
2
1
0
0
С
ростом
количества
апериодических
звеньев,
описывающих
объект,
при
неизменной суммарной постоянной времени Ramp
Tμ, кривая реакции теснее прилегает к оси
времени и при n→бесконечности, совпадает с
этой осью, что характерно для системы с
чистым запаздыванием, равным Tμ.
1
2
3
4
5
6
7
T
1
1
1
s+1
s+1
s+1
1
3s+1
8
9
10

10.

Настройка контуров и их оптимизация
1
Настройка на технический оптимум
Случай 1
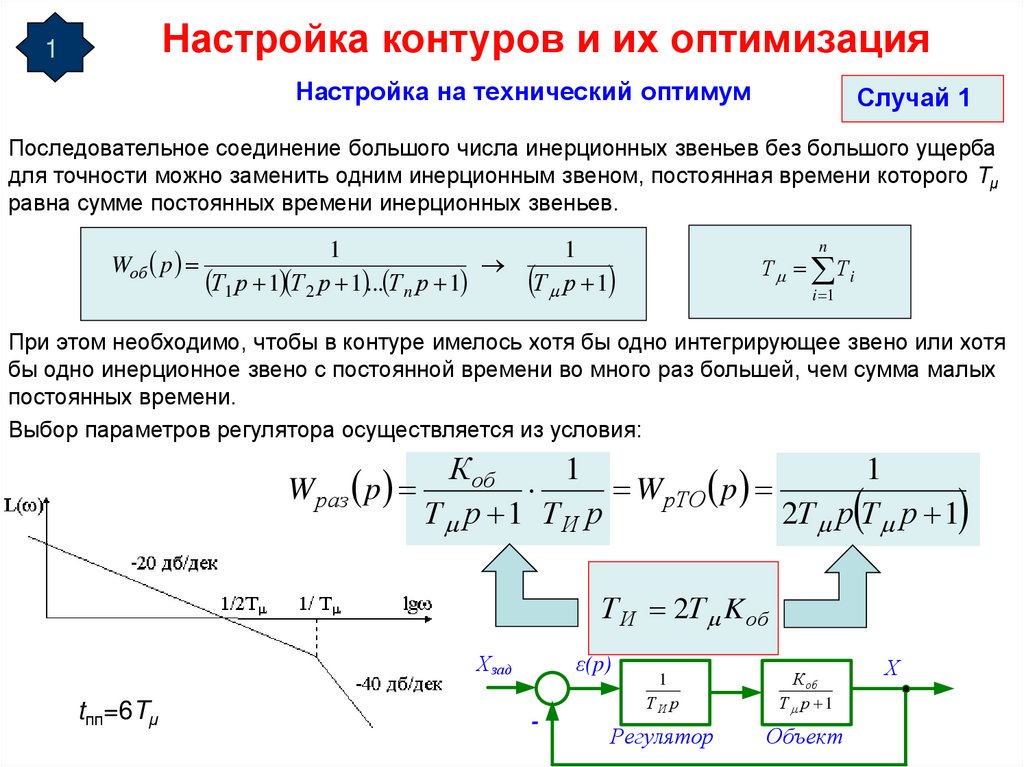
Последовательное соединение большого числа инерционных звеньев без большого ущерба
для точности можно заменить одним инерционным звеном, постоянная времени которого Tμ
равна сумме постоянных времени инерционных звеньев.
Wоб p
1
Т1 р 1 Т 2 р 1 ... Т n р 1
n
1
Т р 1
Т Т i
i 1
При этом необходимо, чтобы в контуре имелось хотя бы одно интегрирующее звено или хотя
бы одно инерционное звено с постоянной времени во много раз большей, чем сумма малых
постоянных времени.
Выбор параметров регулятора осуществляется из условия:
Wраз p
Коб
1
1
WрТО p
Т р 1 ТИ р
2Т р Т р 1
Т И 2Т K об
Хзад
tпп=6Tμ
ε(p)
-
ТИ р
К об
Т р 1
Регулятор
Объект
1
Х

11.

2
Настройка контуров и их оптимизация
Настройка на технический оптимум
Случай 2
Пусть уже рассмотренный объект содержит одно инерционное звено с большой постоянной
времени Т0, такое, что оно больше суммы постоянных времени остальных звеньев.
n
Т 0 Тi
Wоб p
i 1
1
Т 0 р 1 Т1 р 1 Т 2 р 1 ... Т n р 1
При оптимизации такой системы следует принять меры для компенсации этой большой
постоянной с помощью ПИ-регулятора. Заменим звенья с малыми инерционностями
одним эквивалентным звеном, как в первом случае, и добавим ПФ ПИ-регулятора.
n
Т Т i
Wраз p
i 1
Коб
1
К Т р 1
П И
Т 0 р 1 Т р 1
ТИ р
Выбирая время изодрома ТИ=Т0, получим следующую ПФ системы
Условием оптимальной настройки, кроме указанного
выше, будет выражение:
Wраз p
Коб
К
П
Т р 1 Т0 р
Время переходного процесса
Тпп=6Tμ.
1
Коб
КП
Т0
Повышение быстродействия
WрТО p
КП
2Т р Т р 1
Т р 1 Т0 р
2Т Коб
достигается
мерами
по
уменьшению постоянной Tμ.
Т.о., время переходного процесса в контуре, настроенном на технический оптимум, полностью
определяется величиной малой некомпенсированной постоянной времени Tμ.

12.

Настройка контуров и их оптимизация
2
Настройка на технический оптимум
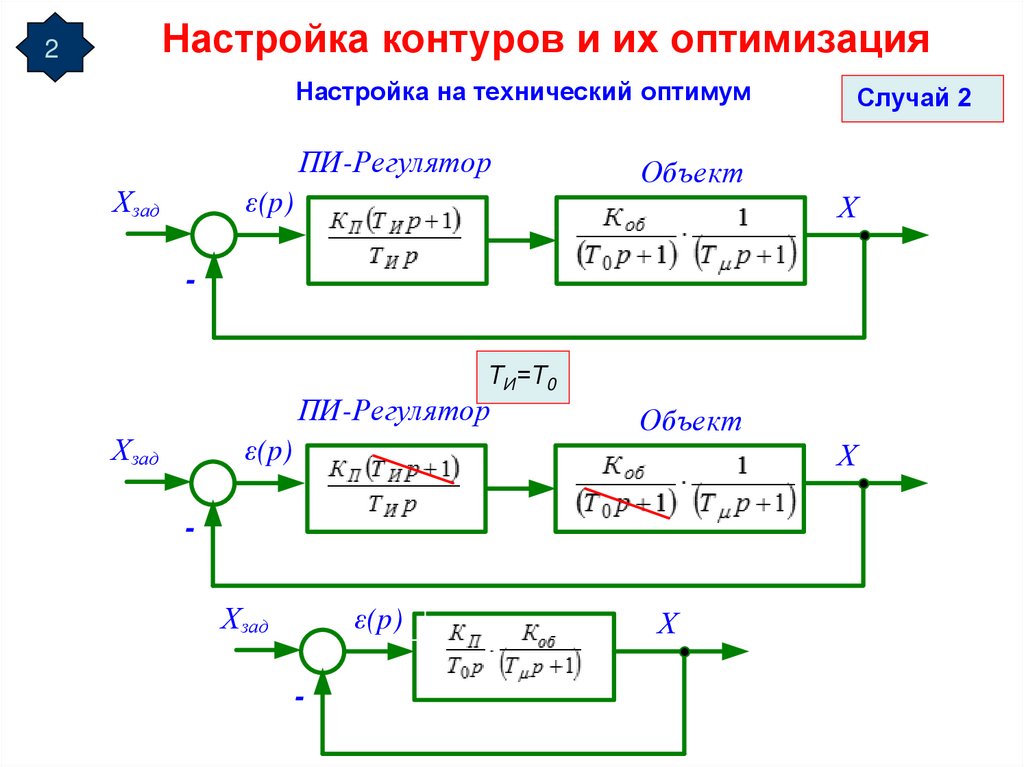
ПИ-Регулятор
Хзад
ε(p)
Случай 2
Объект
Х
ТИ=Т0
ПИ-Регулятор
Хзад
ε(p)
Объект
Х
-
Хзад
ε(p)
-
Х

13.

3
Настройка контуров и их оптимизация
Настройка на технический оптимум
Случай 3
Если в цепочке инерционных звеньев, из которых состоит объект, находятся не одна, а две
большие инерционности Т0 и Т1:
Wоб p
1
Т 0 р 1 Т1 р 1 Т 2 р 1 ... Т n р 1
n
Т 0 Т1 Т i
i 2
Для оптимизации контура следует использовать ПИД-регулятор
Заменим цепочку звеньев с малой инерционностью одним апериодическим звеном первого
порядка с постоянной времени Tμ, и также запишем ПФ разомкнутой системы в виде:
К П Т И р 1 Т Д р 1
К об
1
W раз p
Т 0 р 1 Т1 р 1 Т р 1
Т И р Т р 1
ТИ и ТД, соответственно – время изодрома и время предварения ПИД-регулятора.
Tv – малая некомпенсируемая постоянная времени ПИД-регулятора, необходимая для его реализации.
Выбирая ТИ = Т0 и ТД = Т1, получим:
Wраз p
Коб
КП
Т 0 р Т р 1 Т р 1
В получившейся ПФ присутствует звено запаздывания ПИД-регулятора 1/(Tvp+1),
компенсировать которое не представляется возможным. Однако его можно также
учесть в постоянной времени Tμ эквивалентного апериодического звена.
n
Т Т i Т
*
i 1

14.

3
Настройка контуров и их оптимизация
Настройка на технический оптимум
Случай 3
Тогда условием оптимальной настройки, кроме ТИ и ТД, будет выражение:
2Т *
Т0
Коб К П
КП
Т0
2Т Коб
БОльшую из двух постоянных необходимо всегда компенсировать временем изодрома, а
меньшую - временем предварения. Это связано со спецификой реализации ПИД-регулятора
и взаимосвязанностью параметров его настроек.
Исключение из ПФ разомкнутого контура звеньев с большими и средними постоянными
времени открывает возможности повышения быстродействия контура регулирования. Эта
операция реальные физические инерционные звенья из контура, разумеется, не исключает.
Однако их действие, замедляющее протекание переходных процессов, компенсируется
действием соответствующих форсирующих звеньев, содержащихся в регуляторе,
ускоряющих в требуемой степени реакцию системы.
Пытаться компенсировать весьма малые постоянные времени нецелесообразно, так как
технические трудности компенсации быстро возрастают при уменьшении значений
постоянных времени, а влияние на быстродействие системы данные малые постоянные
времени оказывают весьма слабое.
Время переходного процесса - всё так же 6Tμ. (ТПП=6 Tμ)

15.

Настройка контуров и их оптимизация
Настройка на симметричный оптимум
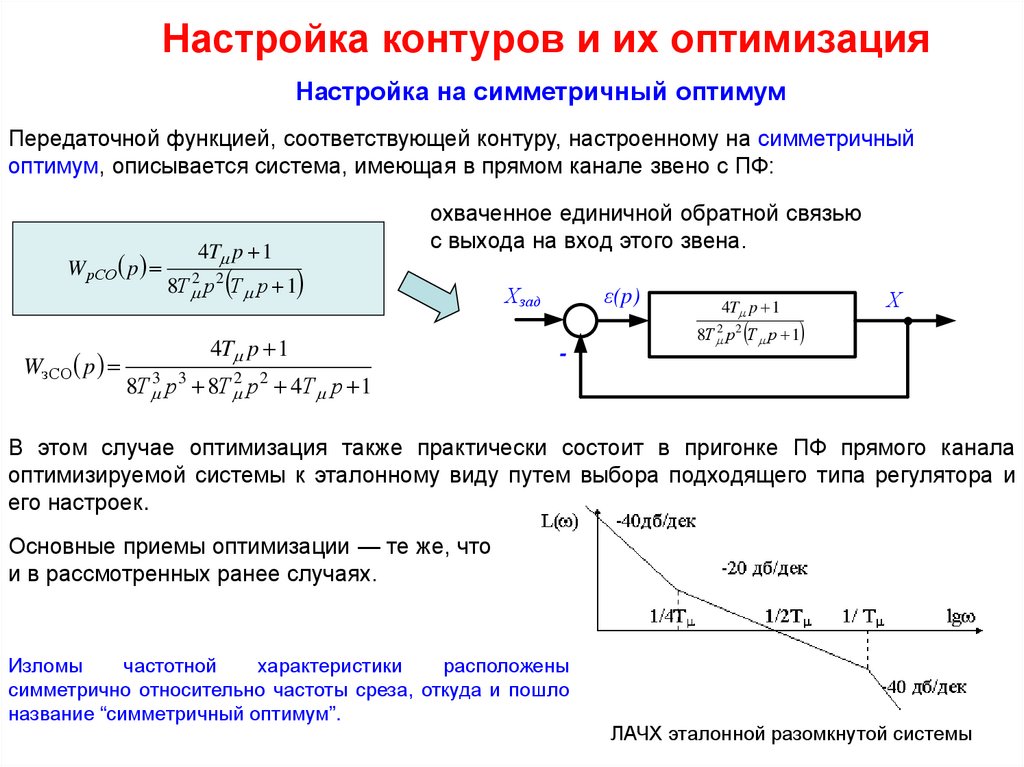
Передаточной функцией, соответствующей контуру, настроенному на симметричный
оптимум, описывается система, имеющая в прямом канале звено с ПФ:
W рСО p
WзСО p
4T p 1
охваченное единичной обратной связью
с выхода на вход этого звена.
8Т 2 р 2 Т р 1
4T p 1
Хзад
ε(p)
-
4T p 1
Х
8Т 2 р 2 Т р 1
8Т 3 р 3 8Т 2 р 2 4Т р 1
В этом случае оптимизация также практически состоит в пригонке ПФ прямого канала
оптимизируемой системы к эталонному виду путем выбора подходящего типа регулятора и
его настроек.
Основные приемы оптимизации — те же, что
и в рассмотренных ранее случаях.
Изломы
частотной
характеристики
расположены
симметрично относительно частоты среза, откуда и пошло
название “симметричный оптимум”.
ЛАЧХ эталонной разомкнутой системы

16.

1
Настройка контуров и их оптимизация
Настройка на симметричный оптимум
Случай 1
Если объект содержит одно интегрирующее и одно инерционное звено первого порядка, в
этом случае для оптимизации контура используется ПИ-регулятор.
K об
Wоб p
p Т об р 1
K об
K Т р 1
П И
p Т об р 1
ТИ р
+ ПИ-регулятор
Если время изодрома регулятора выбрать из условия компенсации постоянной времени
объекта (ТИ = Тоб), то ПФ разомкнутого контура принимает вид:
W раз p
K П Kоб
Т И р2
В этом случае замкнутая единичной обратной связью система будет находиться на границе
устойчивости при любом значении коэффициента передачи Кп.
Компенсировать постоянную времени объекта нельзя. Ее следует принять в качестве
некомпенсируемой постоянной времени Tμ.
Для приведения в соответствие ПФ разомкнутой системы к эталонной остается выполнить
такие условия:
4Т Т И
ТИ
8Т 2
Коб К П
КП
1
2Т Коб

17.

2
Настройка контуров и их оптимизация
Настройка на симметричный оптимум
Случай 2
Если объект содержит интегрирующее звено и ряд инерционных звеньев с соизмеримыми
постоянными времени Тi, то, последние следует заменить одним эквивалентным
апериодическим звеном с эквивалентной постоянной времени.
K об
Wоб p
p Т 0 р 1 Т1 р 1 Т 2 р 1 ... Т n р 1
n
Т Тi
i 1
После чего действовать согласно алгоритму, описанному для случая 1:
применение ПИ-регулятора и соответствующей настройки.
Wраз p
Т И 4Т
Kоб
K Т р 1
П И
p Т р 1
ТИ р
КП
1
2Т К об

18.

Настройка контуров и их оптимизация
3
Настройка на симметричный оптимум
Случай 3
Объект с ПФ общего вида содержит интегрирующее звено и одно инерционное звено с
большОй постоянной времени Т0, такой, что она больше, чем Tμ, т. е. сумма всех остальных
постоянных времени.
n
K об
Wоб p
p Т 0 р 1 Т1 р 1 Т 2 р 1 ... Т n р 1
Т 0 Тi
i 1
При оптимизации компенсируют эту большУю постоянную с помощью ПИД-регулятора
Заменим звенья с малыми инерционностями одним эквивалентным апериодическим звеном
с постоянной времени, включающей сумму всех постоянных времени, т. е. Тμ, а также малую
некомпенсируемую постоянную времени ПИД-регулятора.
n
Т Т i Т
i 1
В этом случае ПФ разомкнутой системы принимает вид:
W раз p
K Т р 1 Т Д р 1
K об
П И
p Т 0 р 1 Т р 1
ТИ р
Kоб
K Т р 1
П И 2
Т р 1
ТИ р
ТИ
И условиями оптимальной настройки будут условия:
8Т 2
К
К
4Т Т И
об П
Тогда, выбирая ТД = Т0, получим:
Wраз p
КП
1
2Т К об

19. СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ

Общие принципы построения СПР
Контур n
gn~xn*
Регулятор n
WPn(p)
g2~x2*
...
Регулятор 2
Регулятор 1
WP2(p)
WP1(p)
g1~x1*
z1~x1
z2~x2
Объект регулирования
Контур 2
Контур 1
u
WО1(p)
x1
WО2(p)
x2
... W (p)
xn-1
xn
Оn
WД1(p)
WД2(p)
:
:
zn~xn
WДn(p)
Датчики
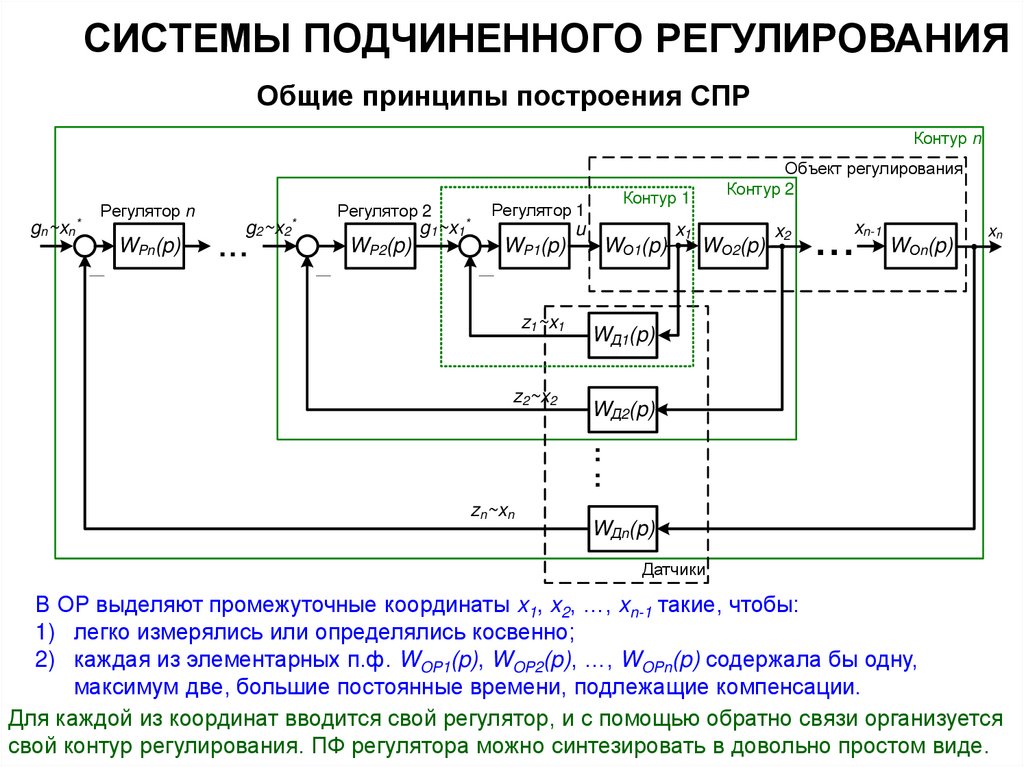
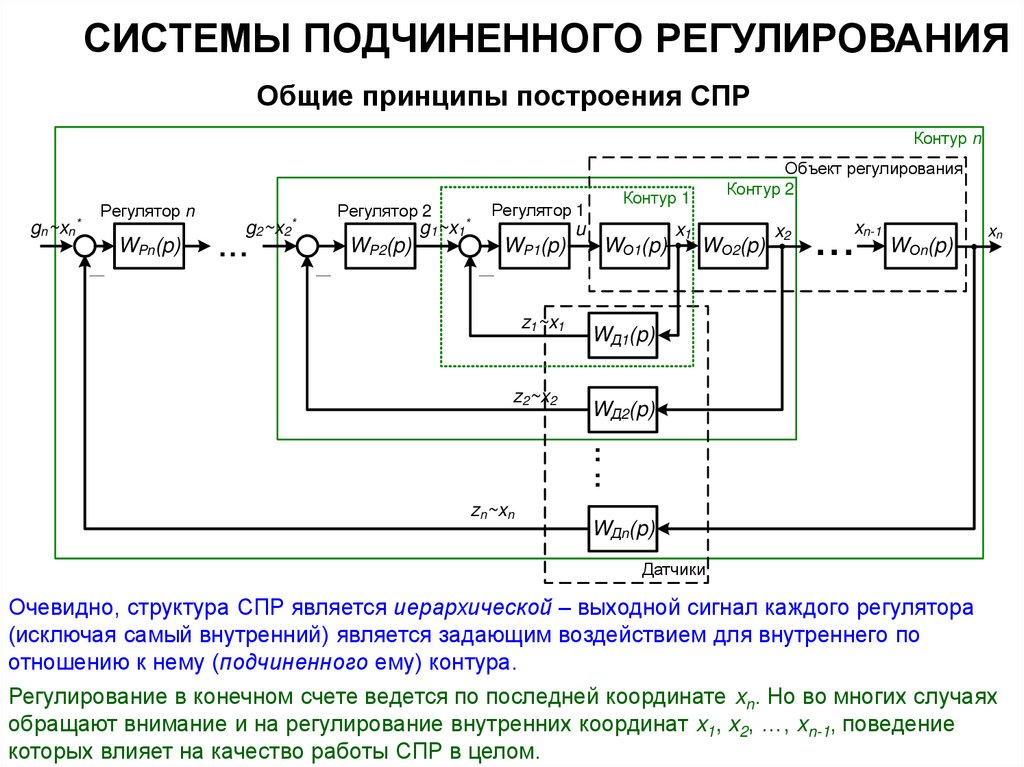
В ОР выделяют промежуточные координаты x1, x2, …, xn-1 такие, чтобы:
1) легко измерялись или определялись косвенно;
2) каждая из элементарных п.ф. WOP1(p), WOP2(p), …, WOPn(p) содержала бы одну,
максимум две, большие постоянные времени, подлежащие компенсации.
Для каждой из координат вводится свой регулятор, и с помощью обратно связи организуется
свой контур регулирования. ПФ регулятора можно синтезировать в довольно простом виде.

20. СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ

Общие принципы построения СПР
Контур n
gn~xn*
Регулятор n
WPn(p)
g2~x2*
...
Регулятор 2
Регулятор 1
WP2(p)
WP1(p)
g1~x1*
z1~x1
z2~x2
Объект регулирования
Контур 2
Контур 1
u
WО1(p)
x1
WО2(p)
x2
... W (p)
xn-1
xn
Оn
WД1(p)
WД2(p)
:
:
zn~xn
WДn(p)
Датчики
Очевидно, структура СПР является иерархической – выходной сигнал каждого регулятора
(исключая самый внутренний) является задающим воздействием для внутреннего по
отношению к нему (подчиненного ему) контура.
Регулирование в конечном счете ведется по последней координате xn. Но во многих случаях
обращают внимание и на регулирование внутренних координат x1, x2, …, xn-1, поведение
которых влияет на качество работы СПР в целом.

21. СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ

Общие принципы построения СПР
Контур n
g2~x2*
Регулятор 2
Регулятор 1
WP2(p)
WP1(p)
g1~x1*
z1~x1
z2~x2
u
Объект регулирования
Контур 2
Контур 1
WО1(p)
x1
WО2(p)
x2
... W (p)
xn-1
xn
Оn
WД1(p)
WД2(p)
Датчики
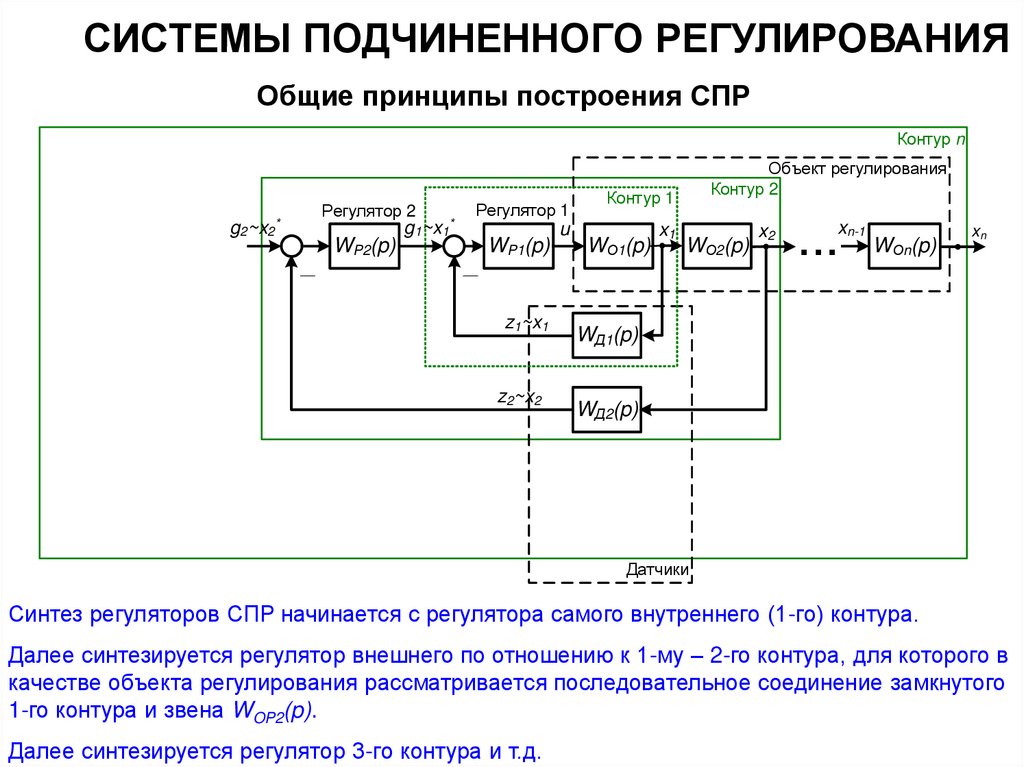
Синтез регуляторов СПР начинается с регулятора самого внутреннего (1-го) контура.
Далее синтезируется регулятор внешнего по отношению к 1-му – 2-го контура, для которого в
качестве объекта регулирования рассматривается последовательное соединение замкнутого
1-го контура и звена WOP2(p).
Далее синтезируется регулятор 3-го контура и т.д.

22. СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ

Общие принципы построения СПР
Контур n
gn~xn*
Регулятор n
WPn(p)
g2~x2*
...
Регулятор 2
Регулятор 1
WP2(p)
WP1(p)
g1~x1*
z1~x1
z2~x2
Объект регулирования
Контур 2
Контур 1
u
WО1(p)
x1
WО2(p)
x2
... W (p)
xn-1
xn
Оn
WД1(p)
WД2(p)
:
:
zn~xn
WДn(p)
Датчики
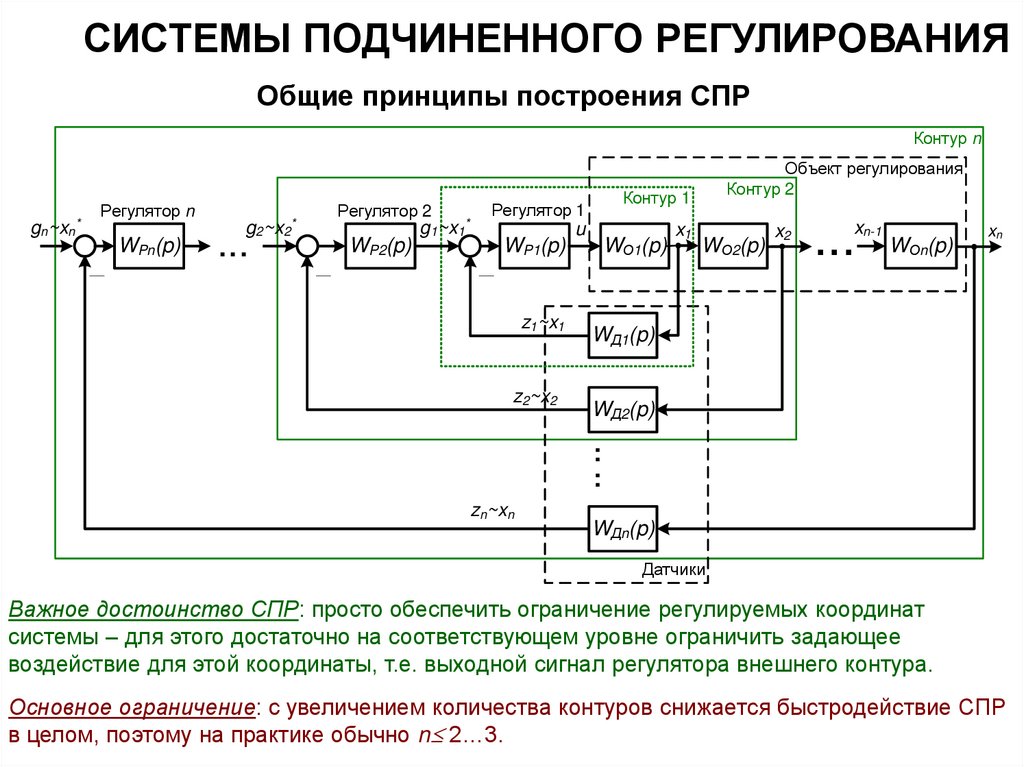
Важное достоинство СПР: просто обеспечить ограничение регулируемых координат
системы – для этого достаточно на соответствующем уровне ограничить задающее
воздействие для этой координаты, т.е. выходной сигнал регулятора внешнего контура.
Основное ограничение: с увеличением количества контуров снижается быстродействие СПР
в целом, поэтому на практике обычно n 2…3.

23.

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ
Каскадные системы управления характеризуются лучшим качеством управления по
сравнению с одноконтурными системами по следующим причинам:
- возмущения, поступающие на части объекта, расположенные ближе к входу,
прежде чем воздействовать на выходную координату X (регулируемую переменную)
предварительно «парируются» во внутренних контурах управления;
- наличие внутренних контуров уменьшает влияние изменения параметров входной
части на динамические качества системы регулирования (снижается чувствительность
системы к изменению параметров объекта);
- поведение регулируемой переменной X становится более быстрым (менее
инертным), если внутренний контур обеспечивает более быстрые собственные движения по
сравнению с исходными.
Еще ограничение: не рекомендуется использовать для объектов, у которых
близки (соизмеримы) постоянный времени, которые хотят компенсировать.
Например, Тя ≈Тм.

24. СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ

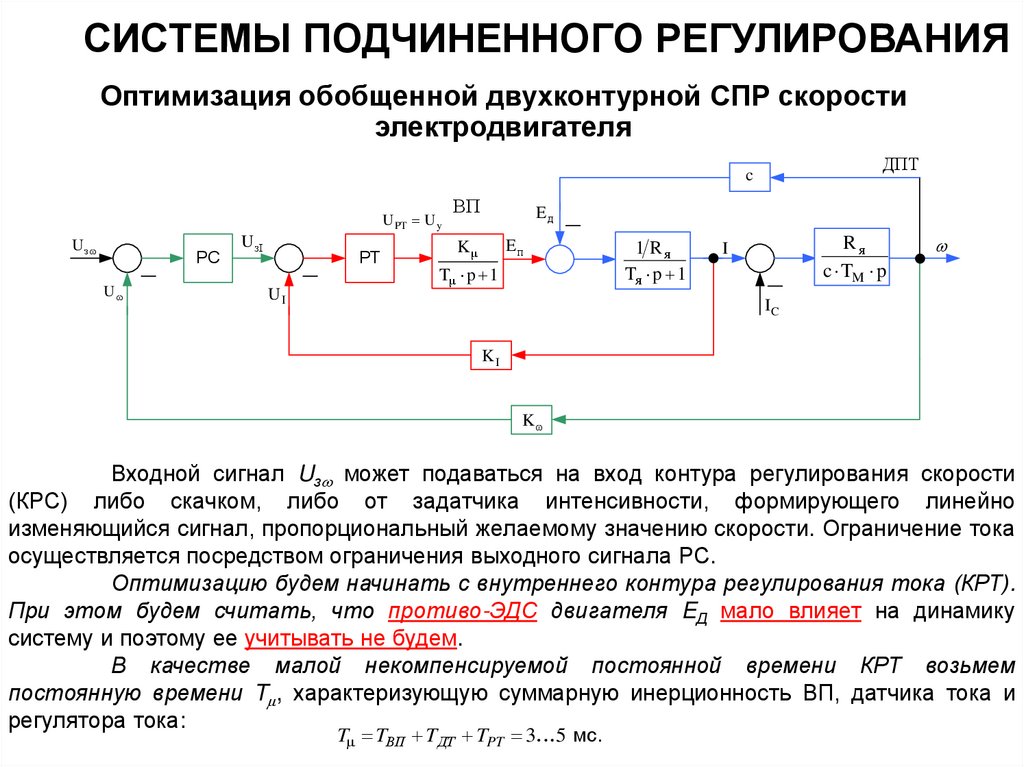
Оптимизация обобщенной двухконтурной СПР скорости
электродвигателя
ДПТ
c
U PT U y
U зω
РС
Uω
U зI
РТ
ВП
Eд
Eп
Kμ
Tμ p 1
UI
1 Rя
Tя p 1
Rя
c TM p
I
IC
KI
Kω
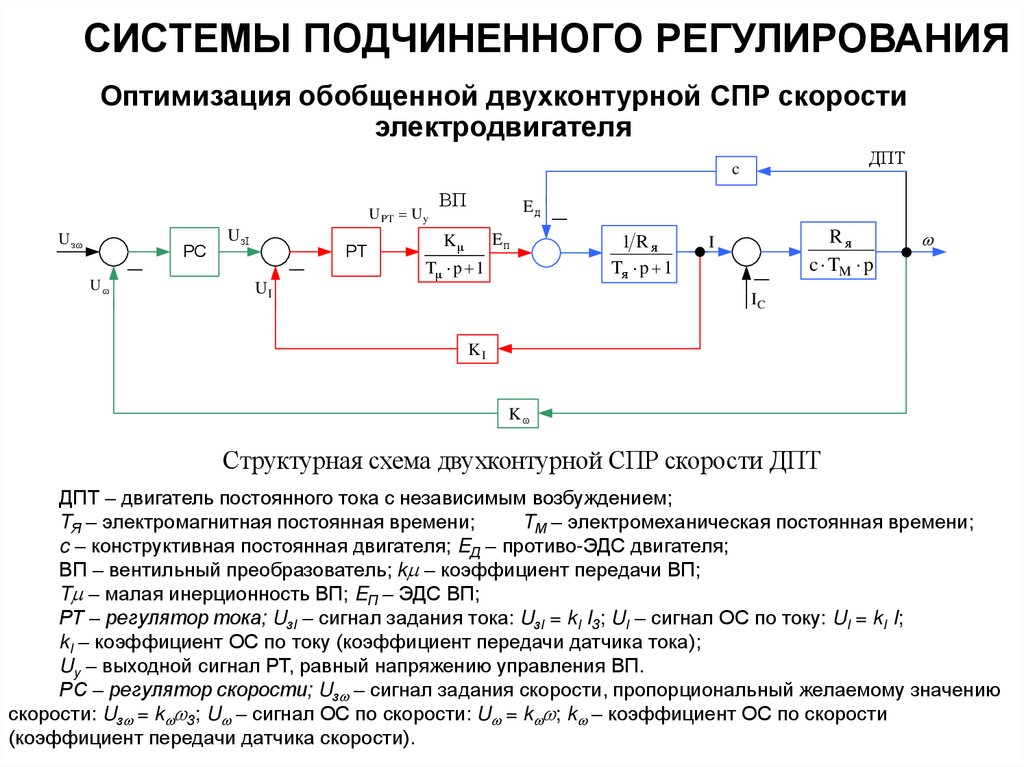
Структурная схема двухконтурной СПР скорости ДПТ
ДПТ – двигатель постоянного тока с независимым возбуждением;
TЯ – электромагнитная постоянная времени;
TМ – электромеханическая постоянная времени;
c – конструктивная постоянная двигателя; EД – противо-ЭДС двигателя;
ВП – вентильный преобразователь; k – коэффициент передачи ВП;
T – малая инерционность ВП; EП – ЭДС ВП;
РТ – регулятор тока; UзI – сигнал задания тока: UзI = kI IЗ; UI – сигнал ОС по току: UI = kI I;
kI – коэффициент ОС по току (коэффициент передачи датчика тока);
Uy – выходной сигнал РТ, равный напряжению управления ВП.
РС – регулятор скорости; Uз – сигнал задания скорости, пропорциональный желаемому значению
скорости: Uз = k З; U – сигнал ОС по скорости: U = k ; k – коэффициент ОС по скорости
(коэффициент передачи датчика скорости).

25.

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ
Оптимизация обобщенной двухконтурной СПР скорости
электродвигателя
ДПТ
c
U PT U y
U зω
РС
Uω
U зI
РТ
ВП
Eд
Eп
Kμ
Tμ p 1
UI
1 Rя
Tя p 1
Rя
c TM p
I
IC
KI
Kω
Входной сигнал Uз может подаваться на вход контура регулирования скорости
(КРС) либо скачком, либо от задатчика интенсивности, формирующего линейно
изменяющийся сигнал, пропорциональный желаемому значению скорости. Ограничение тока
осуществляется посредством ограничения выходного сигнала РС.
Оптимизацию будем начинать с внутреннего контура регулирования тока (КРТ).
При этом будем считать, что противо-ЭДС двигателя EД мало влияет на динамику
систему и поэтому ее учитывать не будем.
В качестве малой некомпенсируемой постоянной времени КРТ возьмем
постоянную времени T , характеризующую суммарную инерционность ВП, датчика тока и
регулятора тока:
T TВП TДТ TPT 3 5 мс.

26.

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ
Оптимизация обобщенной двухконтурной СПР скорости
электродвигателя
РТ
ВП
Tя p 1 R я
U зω
Kμ
Uy
K μ K I TT p
ДПТ
Eд
Eп
Tμ p 1
1 Rя
Tя p 1
UI
KI
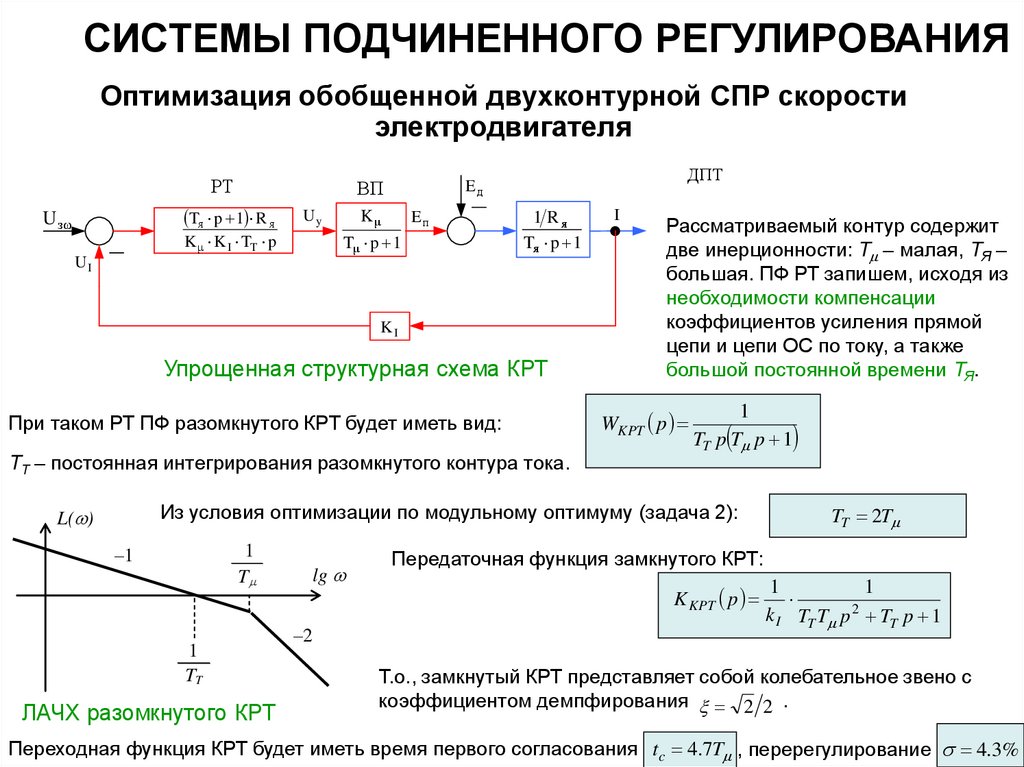
Упрощенная структурная схема КРТ
При таком РТ ПФ разомкнутого КРТ будет иметь вид:
TT – постоянная интегрирования разомкнутого контура тока.
I
Рассматриваемый контур содержит
две инерционности: T – малая, TЯ –
большая. ПФ РТ запишем, исходя из
необходимости компенсации
коэффициентов усиления прямой
цепи и цепи ОС по току, а также
большой постоянной времени TЯ.
WKPT p
1
TT p T p 1
Из условия оптимизации по модульному оптимуму (задача 2):
L( )
1
T
–1
1
TT
ЛАЧХ разомкнутого КРТ
lg
–2
TT 2T
Передаточная функция замкнутого КРТ:
K KPT p
1
1
2
k I TT T p TT p 1
Т.о., замкнутый КРТ представляет собой колебательное звено с
коэффициентом демпфирования 2 2 .
Переходная функция КРТ будет иметь время первого согласования tc 4.7T , перерегулирование 4.3%

27.

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ
Оптимизация обобщенной двухконтурной СПР скорости
электродвигателя
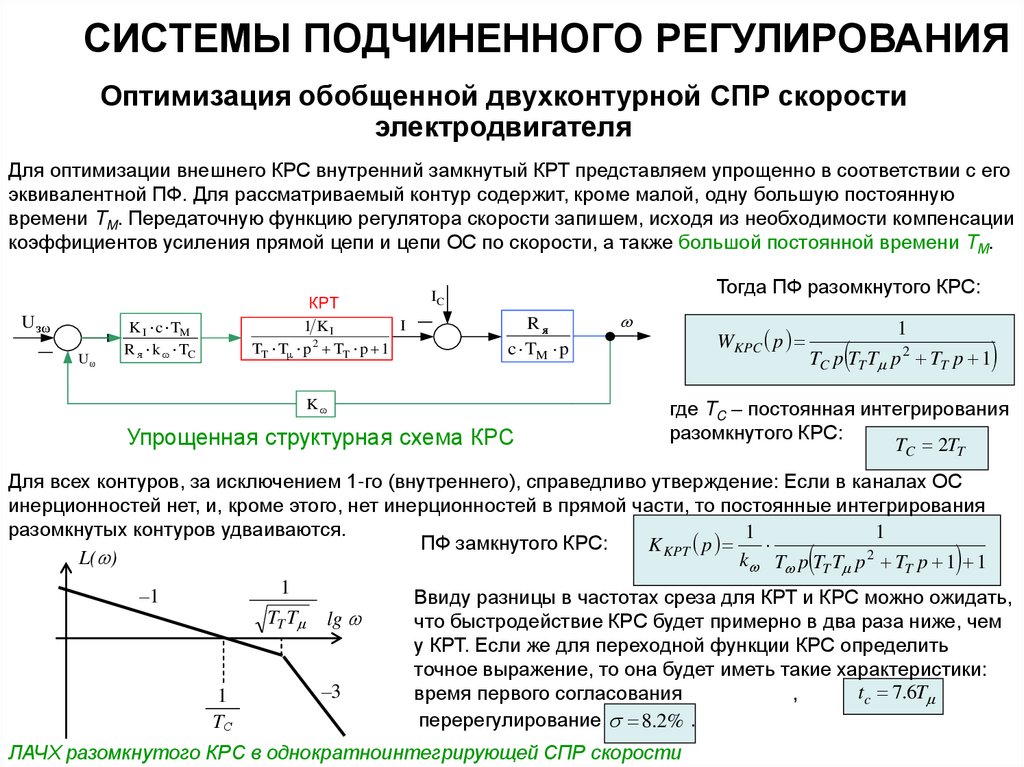
Для оптимизации внешнего КРС внутренний замкнутый КРТ представляем упрощенно в соответствии с его
эквивалентной ПФ. Для рассматриваемый контур содержит, кроме малой, одну большую постоянную
времени TM. Передаточную функцию регулятора скорости запишем, исходя из необходимости компенсации
коэффициентов усиления прямой цепи и цепи ОС по скорости, а также большой постоянной времени TМ.
U зω
Uω
K I c TM
R я k ω TC
КРТ
I
1 KI
2
TT Tμ p TT p 1
Тогда ПФ разомкнутого КРС:
IC
Rя
c TM p
Kω
Упрощенная структурная схема КРС
WKPC p
1
TC p TT T p 2 TT p 1
где TC – постоянная интегрирования
разомкнутого КРС:
TC 2TT
Для всех контуров, за исключением 1-го (внутреннего), справедливо утверждение: Если в каналах ОС
инерционностей нет, и, кроме этого, нет инерционностей в прямой части, то постоянные интегрирования
разомкнутых контуров удваиваются.
1
1
ПФ замкнутого КРС:
K KPT p
L( )
k T p TT T p 2 TT p 1 1
1
–1
Ввиду разницы в частотах среза для КРТ и КРС можно ожидать,
TT T lg
что быстродействие КРС будет примерно в два раза ниже, чем
у КРТ. Если же для переходной функции КРС определить
TТ
точное выражение, то она будет иметь такие характеристики:
–3
tc 7.6T
время первого согласования
,
1
перерегулирование 8.2% .
TС
ЛАЧХ разомкнутого КРС в однократноинтегрирующей СПР скорости

28.

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ
Оптимизация обобщенной двухконтурной СПР скорости
электродвигателя
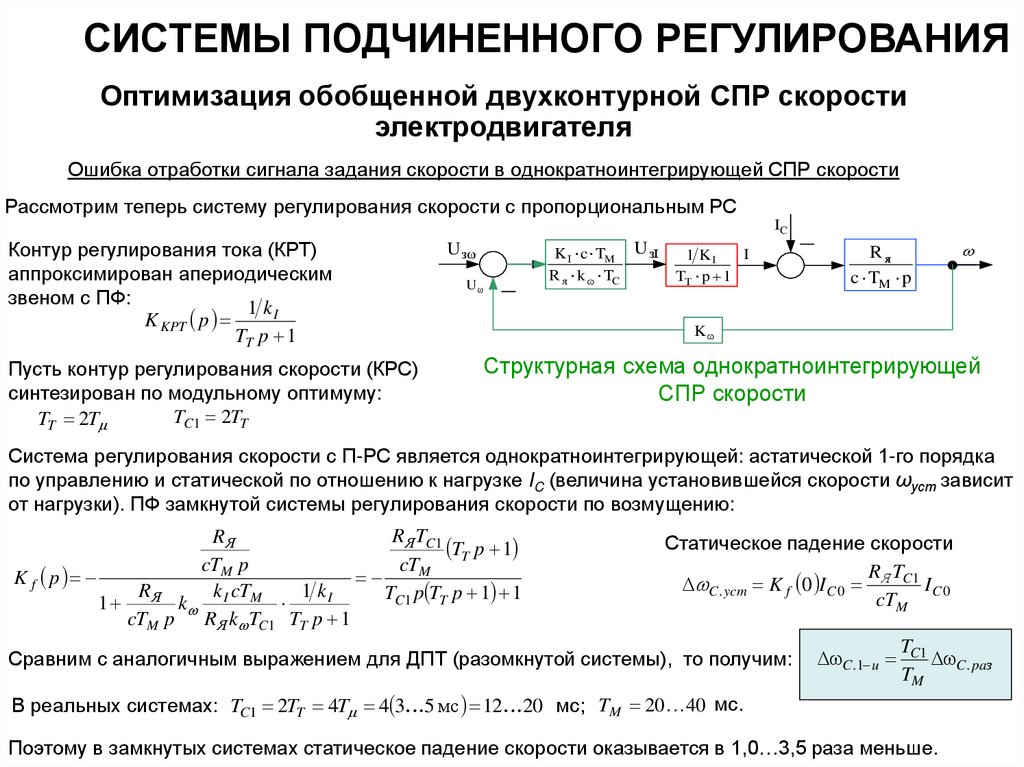
Ошибка отработки сигнала задания скорости в однократноинтегрирующей СПР скорости
Рассмотрим сначала структурную схему ДПТ при питании от преобразователя, которая может
рассматриваться как разомкнутая система регулирования скорости
IC p
E п p
1 Rя
Tя p 1
I p
Rя
c TM p
p
ПФ ДПТ по возмущающему воздействию:
Если считать управляющее воздействие постоянным,
то изменение (падение) скорости в установившемся
режиме:
C. ycm p K f p I C p
K f p
RЯ
cTM p
1
RЯ
1 RЯ
c
cTM p TЯ p 1
RЯ
TЯ p 1
c
TM p TЯ p 1 1
Если считать, что нагрузка изменяется скачком
и является постоянной по величине, то
I
C. ycm p K f p C 0
p
Используя теорему о конечном значении, получаем:
I
C. ycm p lim p C. ycm p lim pK f p C 0 K f 0 I C 0
p 0
p 0
p
Получаем, что статическое падение скорости (по модулю):
C . ycm
RЯ
IC0
c

29.

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ
Оптимизация обобщенной двухконтурной СПР скорости
электродвигателя
Ошибка отработки сигнала задания скорости в однократноинтегрирующей СПР скорости
Рассмотрим теперь систему регулирования скорости с пропорциональным РС
IC
Контур регулирования тока (КРТ)
аппроксимирован апериодическим
звеном с ПФ:
1 kI
K KPT p
TT p 1
Пусть контур регулирования скорости (КРС)
синтезирован по модульному оптимуму:
TC1 2TT
TT 2T
U зω
Uω
K I c TM U зI
R я k ω TC
I
1 KI
TT p 1
Rя
c TM p
Kω
Структурная схема однократноинтегрирующей
СПР скорости
Система регулирования скорости с П-РС является однократноинтегрирующей: астатической 1-го порядка
по управлению и статической по отношению к нагрузке IC (величина установившейся скорости ωуст зависит
от нагрузки). ПФ замкнутой системы регулирования скорости по возмущению:
RЯ TC1
RЯ
TT p 1
cTM p
cTM
K f p
RЯ
k I cTM
1 kI
TC1 p TT p 1 1
1
k
cTM p RЯ k TC1 TT p 1
Статическое падение скорости
R T
C . ycm K f 0 I C 0 Я C1 I C 0
cTM
Сравним с аналогичным выражением для ДПТ (разомкнутой системы), то получим:
В реальных системах: TC1 2TT 4T 4 3 5 мс 12 20 мс; TM 20 40 мс.
T
C.1 u C1 C. paз
TM
Поэтому в замкнутых системах статическое падение скорости оказывается в 1,0…3,5 раза меньше.

30.

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ
Оптимизация обобщенной двухконтурной СПР скорости
электродвигателя
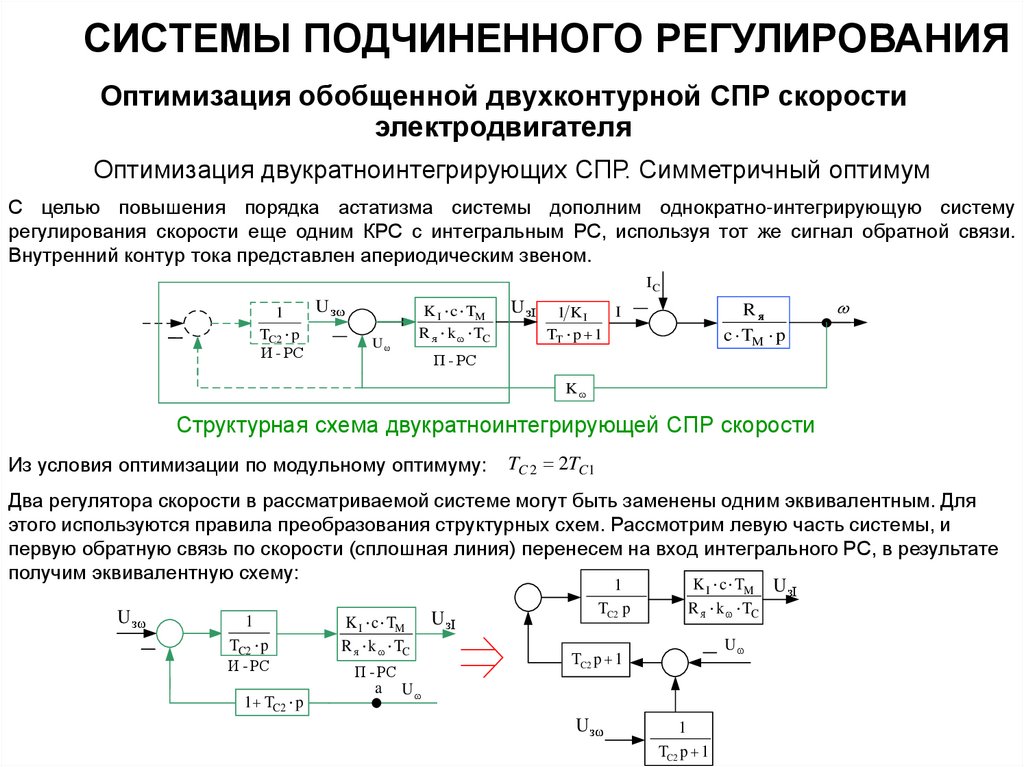
Оптимизация двукратноинтегрирующих СПР. Симметричный оптимум
С целью повышения порядка астатизма системы дополним однократно-интегрирующую систему
регулирования скорости еще одним КРС с интегральным РС, используя тот же сигнал обратной связи.
Внутренний контур тока представлен апериодическим звеном.
IC
1
TC2 p
И - РС
U зω
Uω
K I c TM
R я k ω TC
U зI
Rя
c TM p
I
1 KI
TT p 1
П - РС
Kω
Структурная схема двукратноинтегрирующей СПР скорости
Из условия оптимизации по модульному оптимуму:
TC 2 2TC1
Два регулятора скорости в рассматриваемой системе могут быть заменены одним эквивалентным. Для
этого используются правила преобразования структурных схем. Рассмотрим левую часть системы, и
первую обратную связь по скорости (сплошная линия) перенесем на вход интегрального РС, в результате
получим эквивалентную схему:
K I c TM U зI
1
U зω
1
TC2 p
И - РС
1 TC2 p
K I c TM
R я k ω TC
П - РС
a Uω
U зI
TC2 p
R я k ω TC
Uω
TC2 p 1
U зω
1
TC2 p 1

31.

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ
Оптимизация обобщенной двухконтурной СПР скорости
электродвигателя
Оптимизация двукратноинтегрирующих СПР. Симметричный оптимум
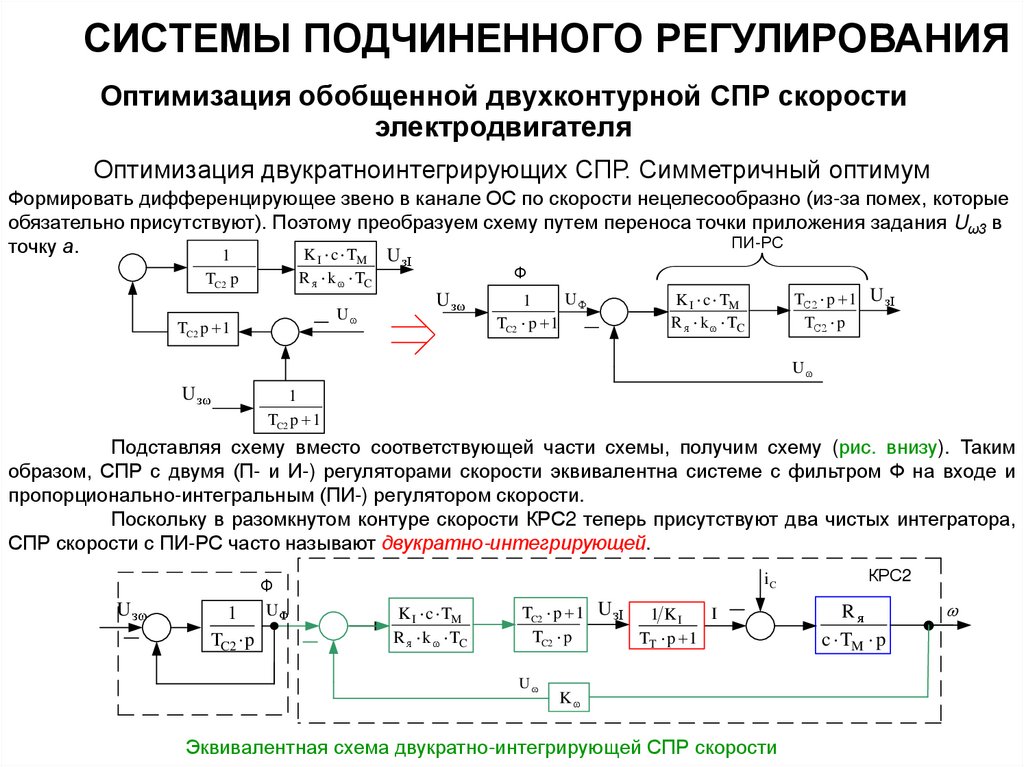
Формировать дифференцирующее звено в канале ОС по скорости нецелесообразно (из-за помех, которые
обязательно присутствуют). Поэтому преобразуем схему путем переноса точки приложения задания UωЗ в
ПИ-РС
точку а.
K c T
1
U
I
M
R я k ω TC
TC2 p
Uω
TC2 p 1
зI
Ф
U зω
UФ
1
TC2 p 1
TС2 p 1 U зI
TС2 p
K I c TM
R я k ω TC
Uω
U зω
1
TC2 p 1
Подставляя схему вместо соответствующей части схемы, получим схему (рис. внизу). Таким
образом, СПР с двумя (П- и И-) регуляторами скорости эквивалентна системе с фильтром Ф на входе и
пропорционально-интегральным (ПИ-) регулятором скорости.
Поскольку в разомкнутом контуре скорости КРС2 теперь присутствуют два чистых интегратора,
СПР скорости с ПИ-РС часто называют двукратно-интегрирующей.
U зω
1
TC2 p
Ф
UФ
iC
K I c TM
R я k ω TC
TC2 p 1 U зI
I
1 KI
TC2 p
TT p 1
Uω
Kω
Эквивалентная схема двукратно-интегрирующей СПР скорости
КРС2
Rя
c TM p

32.

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ
Оптимизация обобщенной двухконтурной СПР скорости
электродвигателя
Оптимизация двукратноинтегрирующих СПР. Симметричный оптимум
Оценим точность двукратно-интегрирующей СПР.
Сам контур скорости КРС2 является астатическим 2-го порядка по управлению и астатическим 1-го
порядка по возмущению. Фильтр на входе системы, представленный детализированной схемой, является
астатическим 1-го порядка, поэтому и вся система окажется астатической 1-го порядка по управлению.
Ошибка при отработке линейного воздействия обусловлена именно ошибкой воспроизведения фильтром
входного сигнала:
p U З p UФ p U З p
1
T p
U З p C 2 U З p .
TC 2 p 1
TC 2 p 1
UЗω(t)=kωat
Используя теорему о конечном значении:
уст lim p p lim p
p 0
ПФ разомкнутого КРС2:
p 0
UФ(t)
уст
TC 2 p
T p k a
U З p lim p C 2
k aTC 2 .
p 0 TC 2 p 1 p 2
TC 2 p 1
W KPC 2 p
U p TC 2 p 1
1
U Ф p
TC 2 p TC1 p TT p 1
где при настройке по модульному оптимуму
TC1 2TT
TC 2 2TC1 4TT
Используя правило оперативного определения частоты среза, можно найти
C
1
1
TC1 2TT
t

33.

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ
Оптимизация обобщенной двухконтурной СПР скорости
электродвигателя
Оптимизация двукратноинтегрирующих СПР. Симметричный оптимум
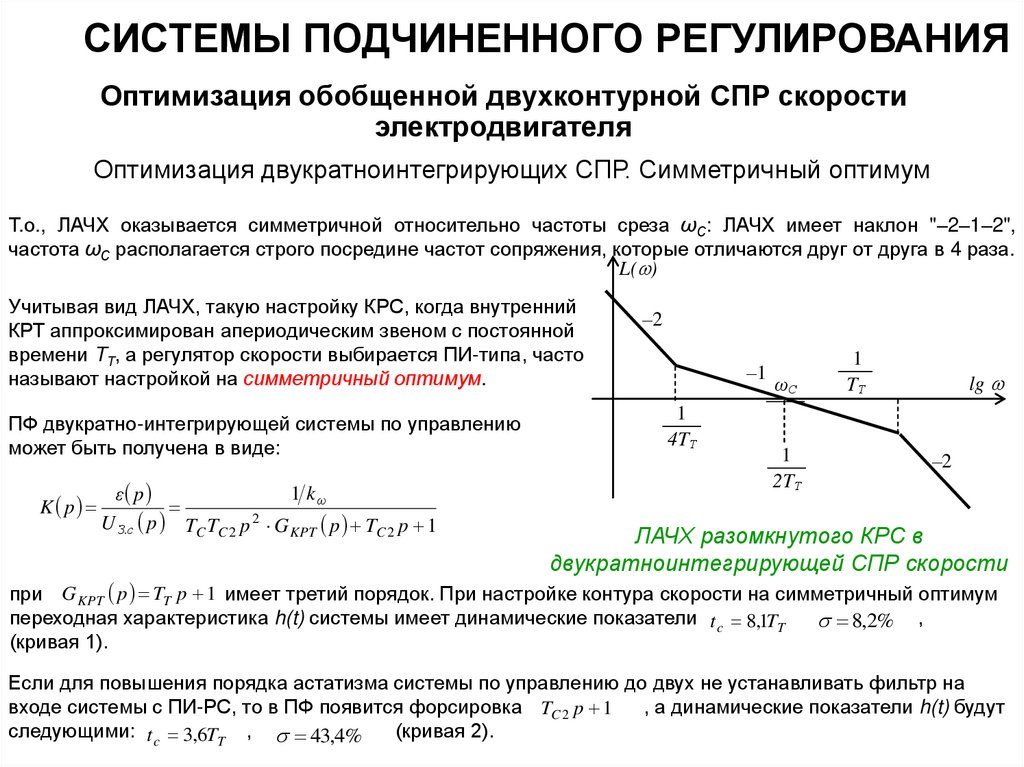
Т.о., ЛАЧХ оказывается симметричной относительно частоты среза ωС: ЛАЧХ имеет наклон "–2–1–2",
частота ωС располагается строго посредине частот сопряжения, которые отличаются друг от друга в 4 раза.
L( )
Учитывая вид ЛАЧХ, такую настройку КРС, когда внутренний
КРТ аппроксимирован апериодическим звеном с постоянной
времени TT, а регулятор скорости выбирается ПИ-типа, часто
называют настройкой на симметричный оптимум.
ПФ двукратно-интегрирующей системы по управлению
может быть получена в виде:
K p
1 kω
ε p
U З.с p TC TC 2 p 2 G KPT p TC 2 p 1
–2
–1
1
4TТ
ωС
1
2TТ
1
TТ
lg
–2
ЛАЧХ разомкнутого КРС в
двукратноинтегрирующей СПР скорости
при G KPT p TT p 1 имеет третий порядок. При настройке контура скорости на симметричный оптимум
переходная характеристика h(t) системы имеет динамические показатели t c 8,1TT
8,2% ,
(кривая 1).
Если для повышения порядка астатизма системы по управлению до двух не устанавливать фильтр на
входе системы с ПИ-РС, то в ПФ появится форсировка TC 2 p 1
, а динамические показатели h(t) будут
следующими: t c 3,6TT , 43,4%
(кривая 2).

34.

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ
Оптимизация обобщенной двухконтурной СПР скорости
электродвигателя
Оптимизация двукратноинтегрирующих СПР. Симметричный оптимум
1.6
h(t)
1.4
2=43,4%
1.2
1.4
2
4=53,7% 4
1.2
1
3=6,2%
1
0.8
1
1=8,2%
0.8
0.6
0.6
0.4
0.4
0.2
0
h(t)
1.6
5
10
tc4=6,9T
tc3=15,3T
0.2
tc2=3,6TT
tc1=8,1TT
0
3
t/TT
15
20
25
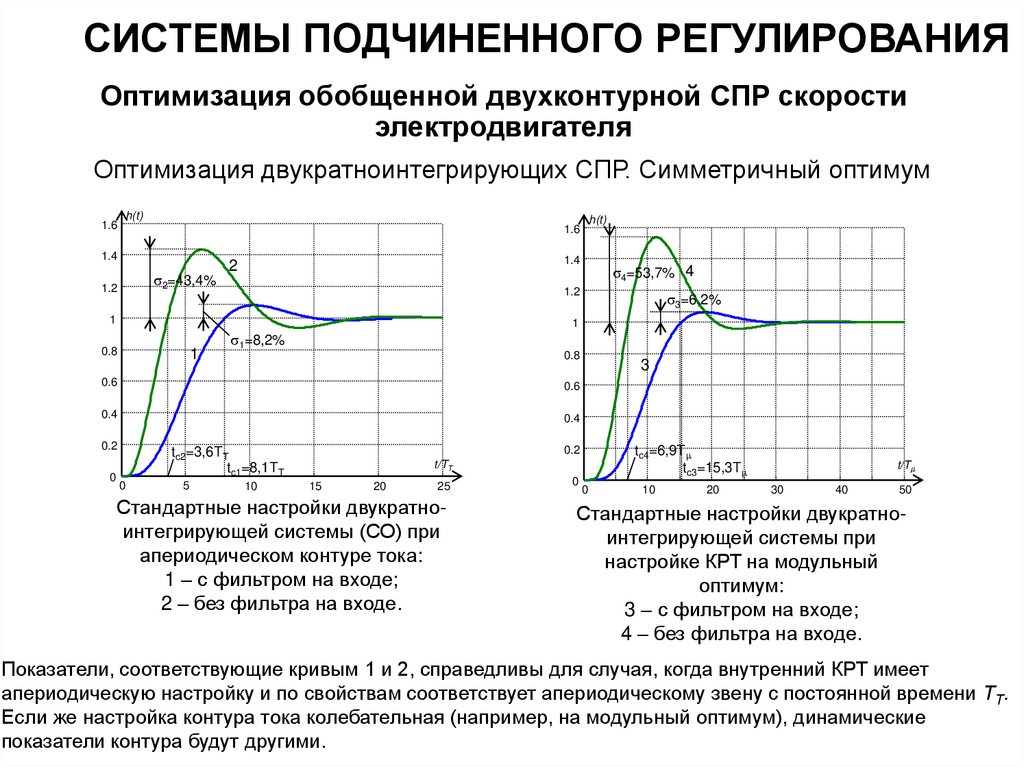
Стандартные настройки двукратноинтегрирующей системы (СО) при
апериодическом контуре тока:
1 – с фильтром на входе;
2 – без фильтра на входе.
0
0
10
20
t/T
30
40
50
Стандартные настройки двукратноинтегрирующей системы при
настройке КРТ на модульный
оптимум:
3 – с фильтром на входе;
4 – без фильтра на входе.
Показатели, соответствующие кривым 1 и 2, справедливы для случая, когда внутренний КРТ имеет
апериодическую настройку и по свойствам соответствует апериодическому звену с постоянной времени ТТ.
Если же настройка контура тока колебательная (например, на модульный оптимум), динамические
показатели контура будут другими.

35.

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ
Оптимизация обобщенной двухконтурной СПР скорости
электродвигателя
Оптимизация двукратноинтегрирующих СПР. Симметричный оптимум
/ З
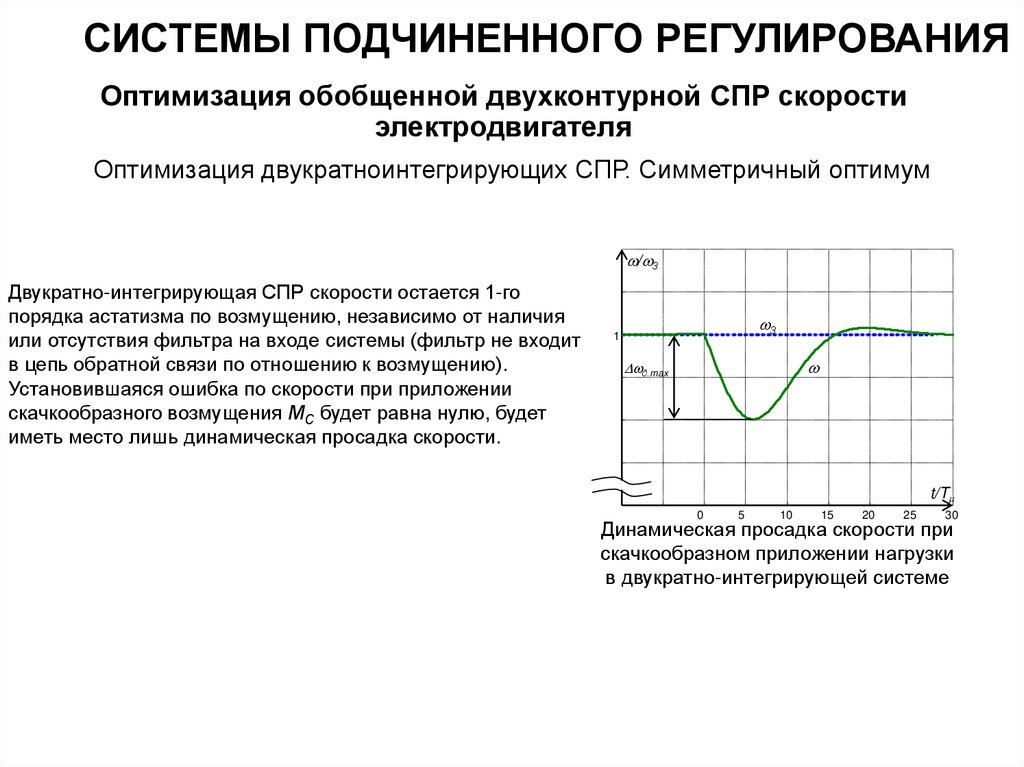
Двукратно-интегрирующая СПР скорости остается 1-го
порядка астатизма по возмущению, независимо от наличия
или отсутствия фильтра на входе системы (фильтр не входит
в цепь обратной связи по отношению к возмущению).
Установившаяся ошибка по скорости при приложении
скачкообразного возмущения МС будет равна нулю, будет
иметь место лишь динамическая просадка скорости.
З
1
д.max
t/T
0
5
10
15
20
25
30
Динамическая просадка скорости при
скачкообразном приложении нагрузки
в двукратно-интегрирующей системе