Базовые логические операции и их таблицы истинности. Лекция №3

1. Базовые логические операции и их таблицы истинности

Лекция №3
БАЗОВЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ И
ИХ ТАБЛИЦЫ ИСТИННОСТИ

2. Основные определения

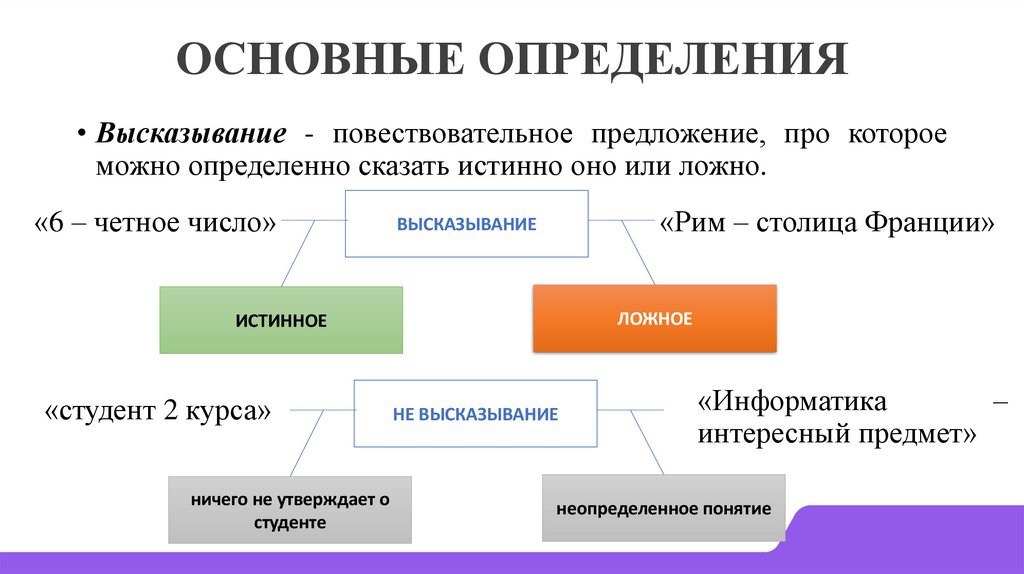
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
• Высказывание - повествовательное предложение, про которое
можно определенно сказать истинно оно или ложно.
«6 – четное число»
«Рим – столица Франции»
ВЫСКАЗЫВАНИЕ
ЛОЖНОЕ
ИСТИННОЕ
«студент 2 курса»
ничего не утверждает о
студенте
НЕ ВЫСКАЗЫВАНИЕ
«Информатика
–
интересный предмет»
неопределенное понятие

3. Основные определения

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
• Логические операции - мыслительные действия, результатом
которых является изменение содержания или объема понятий, а
также образование новых понятий.
• Логическое выражение - устное утверждение или запись, в
которое, наряду с постоянными величинами, обязательно входят
переменные величины (объекты).
• Сложное логическое выражение - логическое выражение,
состоящее из одного или нескольких простых логических
выражений (или сложных логических выражений), соединенных
с помощью логических операций.

4. Логические операции и таблицы истинности

ЛОГИЧЕСКИЕ ОПЕРАЦИИ И
ТАБЛИЦЫ ИСТИННОСТИ

5. Конъюнкция

КОНЪЮНКЦИЯ

6.

01
• Конъюнкция - логическое выражение, которое
считается истинным в том и только том случае, когда
оба простых выражения являются истинными, во
всех остальных случаях выражение ложно.
• Обозначение:
• Читается: «и»
F =A& B
F=A^B
F=A∙B

7.

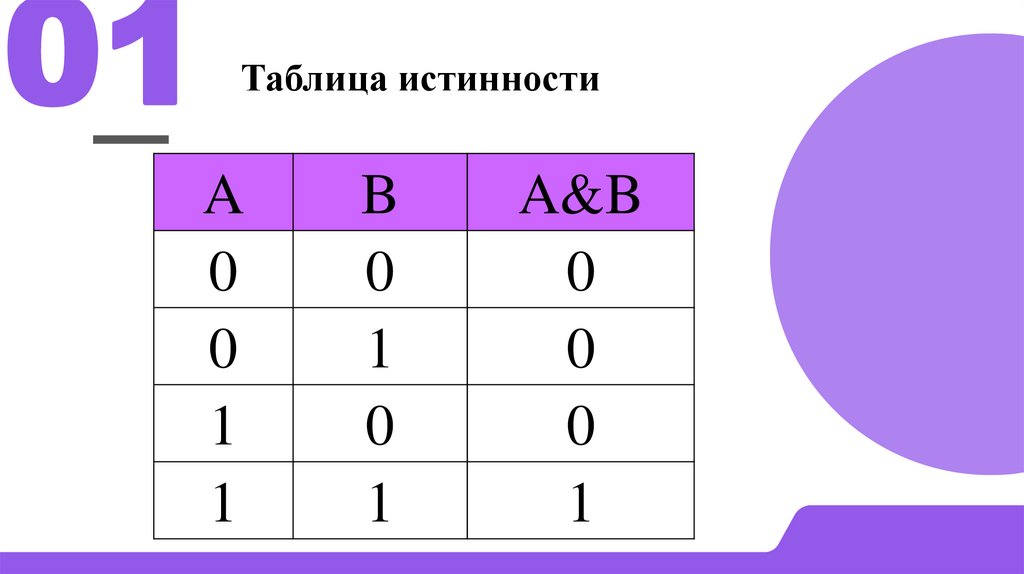
01
Таблица истинности
A
0
0
1
1
B
0
1
0
1
A&B
0
0
0
1

8. Дизъюнкция

ДИЗЪЮНКЦИЯ

9.

02
• Дизъюнкция - логическое выражение, которое
истинно, если хотя бы одно из простых логических
выражений истинно и ложно тогда и только тогда,
когда оба простых логических выражения ложны.
• Обозначение:
F =AvB
F =A+ B
• Читается: «или»

10.

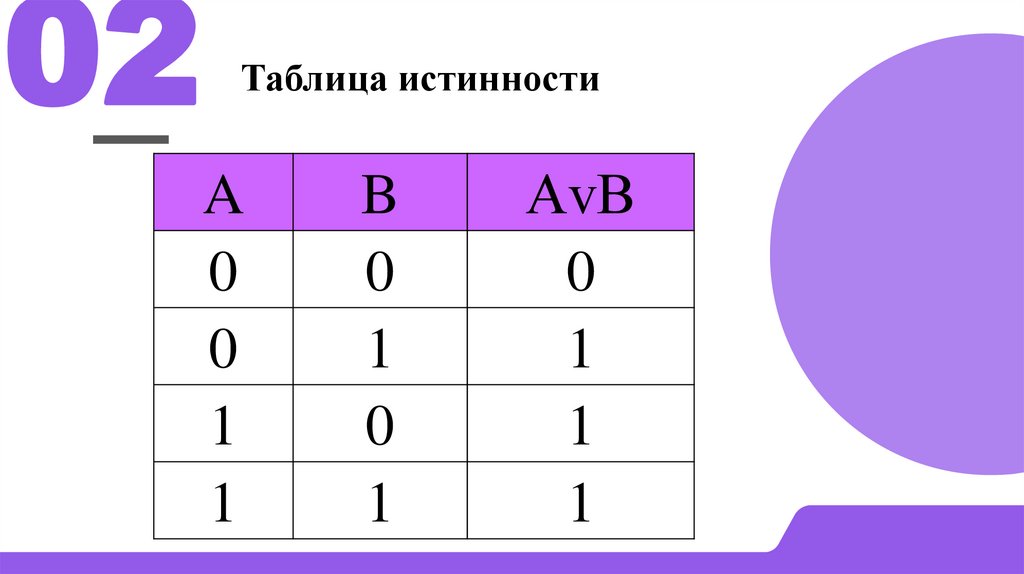
02
Таблица истинности
A
0
0
1
1
B
0
1
0
1
AⅴB
0
1
1
1

11. Инверсия

ИНВЕРСИЯ

12.

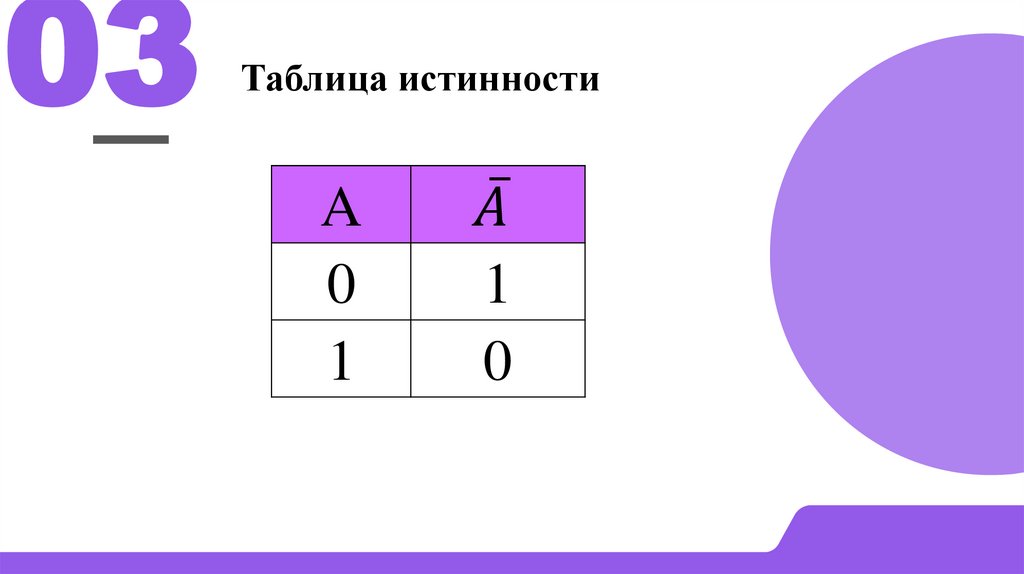
03
• Инверсия - логическое выражение, если исходное
выражение истинно, то результат отрицания будет
ложным, и наоборот, если исходное выражение
ложно, то результат отрицания будет истинным.
• Обозначение:
F = ¬A
F =