Similar presentations:
Логические операции. Построение таблиц истинности
1.
Логическиеоперации.
Построение таблиц
истинности
Цель: узнать что такое логика?
какая существует связь между двоичным
кодированием и алгеброй логики? как можно
использовать логические операции?
2.
Введение• Слово «логика» произошло от греческих слов «легос»
и «логос». «Легос» означает – «говорить»,
«пояснять», «логос» – «мудрость».
• Логикой называется наука о формах и законах
правильного мышления.
• Мышление – высшая форма познавательной
деятельности человека. Правильное мышление
играет решающую роль в деятельности людей. Чтобы
человек правильно мыслил, он должен подчиняться
определенным правилам и закономерностям.
3.
ВведениеОсновные формы мышления:
• Понятие – это форма мышления, которая отражает
существенные признаки предметов. Объем понятия может
быть представлен как множество объектов. Основу
современной математики составляют логика и теория
множеств.
• Высказывание – это форма мышления, содержащая
утверждение или отрицание чего-либо. Высказывания
могут быть ложными или истинными. Вопросительные и
побудительные предложения не выражают высказываний.
Высказывания бывают простыми и сложными.
• Умозаключение – это форма мышления, при которой
мысль формируется в результате синтеза и обработки
нескольких высказываний и понятий.
4.
ВведениеОснователь логической алгебры - Джордж Буль. Он
изобрел своеобразную алгебру – систему обозначений и
правил, применимую к объектам, числам, буквам и
предложениям.
В основе булевой алгебры лежат операции
конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ).
В XX веке ученые объединили двоичную систему
счисления с алгеброй логики Джорджа Буля, создав тем
самым основу для разработки современного цифрового
электронного компьютера.
5.
ЛогикаВысказывание в математической логике может быть
истинным или ложным, третий случай не
рассматривается.
Если обозначим «истину» как 1, «ложь» как 0, тогда
можно выполнять операции с 1 и 0 или, другими
словами, в двоичном коде.
Алгебра логики – математический аппарат записи
логических высказываний, вычислений, упрощений и
преобразований.
Алгебра логики определяет правила вычислений
логических условий 1 (истина) и 0 (ложь).
6.
Логические операцииЛогическое сложение (дизъюнкция, показывается
символом ∨). Операция, соединяющая два или более
высказываний при помощи операции «ИЛИ»
(например, «А или В») называется логическим
сложением, или дизъюнкцией. Дизъюнкция в обычном
языке означает «или (or)».
Таблица 1
Дизъюнкция
A
B
A˅B
0
0
0
1
0
1
0
1
1
1
1
1
7.
Логические операцииЛогическое умножение (конъюнкция, обозначается
символом ∧). Операция, связывающая два или более
высказываний при помощи операции «И», называется
логическим умножением или конъюнкцией.
Конъюнкция в обычном языке означает «и (and)»
Таблица 2
Конъюнкция
A
B
A˄B
0
0
0
1
0
0
0
1
0
1
1
1
8.
Логические операцииЛогическое отрицание (инверсия). Отрицание «НЕ»,
которым логическое высказывание обращается в
обратное, называется логическим отрицанием или
инверсией (таблица 3). Инверсия в обычном языке
соответствует выражениям «неверно», «обращение в
обратное» и приставке «не (not)».
Таблица 3
Инверсия
A
B
0
1
1
0
9.
Задания для закрепления:Задание № 1.
Обратите в противоположное следующие высказывания.
1. Четные числа бывают простыми.
2. Самат выполнил заданные ему пять заданий.
Задание № 2.
Даны следующие простые высказывания.
1) А = {Монитор – устройство для печати информации на
бумаге},
2) В = {Принтер – устройство для ввода информации},
3) С = {Процессор – устройство обработки информации},
4) D = {Мышь – устройство хранения информации},
Используя таблицы 1, 2, 3 найдите значения следующих
логических операций. 1) (А∧В) 2) (С∨D) 3) (В∧С).
10.
Таблица истинностиТаблица истинности – это таблица, в которой
представлены все значения, которые может принимать
высказывание при всех возможных значениях простых
высказываний, входящих в нее. В таблице истинности
отражаются четыре возможных исхода для двух
переменных. Это пары:
(0, 0), (0, 1), (1, 0), (1, 1).
Если в формуле три переменных, то количество
возможных комбинаций будет равно 8-ми, так как 23= 8.
(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1),
(1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1,1).
11.
Логическое выражениеЛогическое выражение – это составное
выражение, записанное в виде формулы.
При решении задач с логическими
высказываниями необходимо построение таблицы
истинности.
Приоритеты при выполнении логических
операций
1) выражения в скобках;
2) инверсия;
3) конъюнкция;
4) дизъюнкция.
12.
Алгоритм построения таблицыистинности для логических
элементов
1. Определить количество переменных n в логическом
выражении.
2. Подсчитать количество строк m=2n , n – количество
переменных.
3. Подсчитать количество логических операций в
выражении.
4. Для подсчета количества столбцов в таблице сложить
число переменных и число логических операций.
5. Установить последовательность выполнения логических
операций с учетом приоритетов.
6. Выписать наборы входных переменных.
7. Заполнить таблицы.
13.
ПримерДля высказываний А = {22 – четное число} и В = {3 – четное
число} вычислите значения логических операций.
Пояснение решения задачи:
1. Если применить для двух простых высказываний
операцию (И) А∧В, тогда высказывание А – истинно, так как
число 22 – четное. А высказывание В – ложно, так как 3 –
нечетное число. Таким образом, согласно правилу для
операции И будет 1∧0 =0 (ложь).
2. Если применить для двух простых высказываний
операцию (ИЛИ) А∨В, тогда высказывание А – истинно, тогда
как В – ложно. Таким образом, операция 1∨0 =1 (Истина).
3. Если высказывание А подвергнуть инверсии, то оно
будет ложным, так как обратится в высказывание «число 22
нечетное». Точно так же инверсия высказывания В «число 3
нечетное» будет истинным.
A∧B
Ложь (0)
A∨B
Истина (1)
A
Ложь (0)
B
Истина(1)
14.
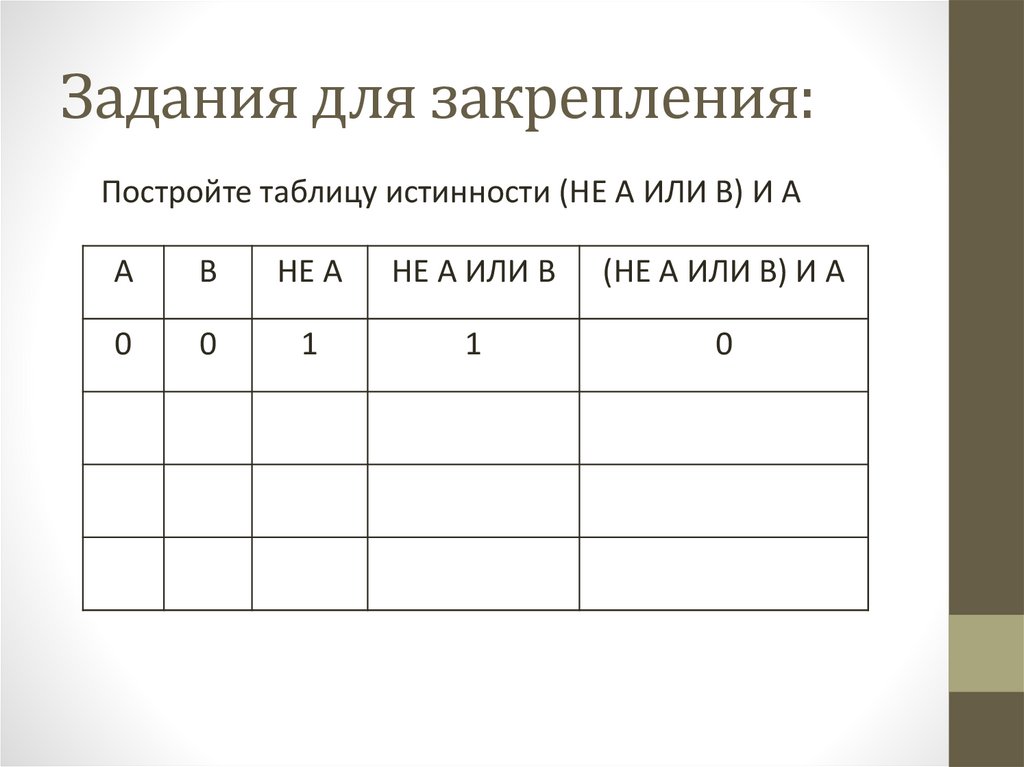
Задания для закрепления:Постройте таблицу истинности (НЕ А ИЛИ В) И А
А
В
НЕ А
НЕ А ИЛИ В
(НЕ А ИЛИ В) И А
0
0
1
1
0
15.
Домашнее задание:Уровень А.
Найдите значения логических функций, приведенных ниже.
1) F = ((0>5) and (2>3)) or(4<5))
2) F = (1<5) and (1>0)
3) F = (3>2) or (3<1)
4) F = (3>2) or (2>0)
5) F = ((1>2) or (1<0)) and((–1>2) or (–1<0))
6) F = (2>5) and (2>3)
7) F = not (5>6)
8) F = not (6>5)
9) F = (2=0) or (2>0)
10) F = (3>0) or (2>0)
Примечание. Образец выполнения задания представлен в
таблице.
0>4
2>5
4<7
(0>4) and (2>5)
F = (0>4) and (2>5) or(4<7)
0
0
1
0
1
16.
Домашнее задание:Уровень В.
Найдите значения логических функций, приведенных ниже.
1. F = (1∨1)∨(1∨0)
2. F = (0∧0)∧(1∧1)
3. F = (0∧1)∨(0∧1)
4. F = (0∨0)∧(1∧1)
5. F = (1∨0)∧(0∧1)
Уровень С.
Даны высказывания – А = {4+19=21} и B = {8 + 3 = 9}.
Определите истинность следующих выражений:
А∧В, А, В, А∨В















 informatics
informatics








