Similar presentations:
Логические выражения и логические операции
1. «Логические выражения и логические операции»
2. Цели урока:
Познакомиться с основнымилогическими выражениями
Познакомиться с порядком
выполнения логических операций в
сложном логическом выражении.
3. Вопросы для повторения:
- Что изучает логика?- Что понимается под высказыванием?
- Что понимается под утверждением?
- Дать определение понятию
рассуждение?
- Что за понятие умозаключение?
- Дать определение понятию
логическое выражение?
4. Основные логические операции:
Конъюнкция (A ^ B)Дизъюнкция (A V B)
Инверсия ( A )
Импликация (A => B)
Эквивалентность ( A <=> B)
5.
1. Конъюнкция (логическоеумножение, & или ^, «И») - ставит в
соответствие двум простым
логическим выражениям новое сложное логическое выражение,
которое будет истинным тогда и
только тогда, когда истинны оба
исходных (простых) логических
выражения.
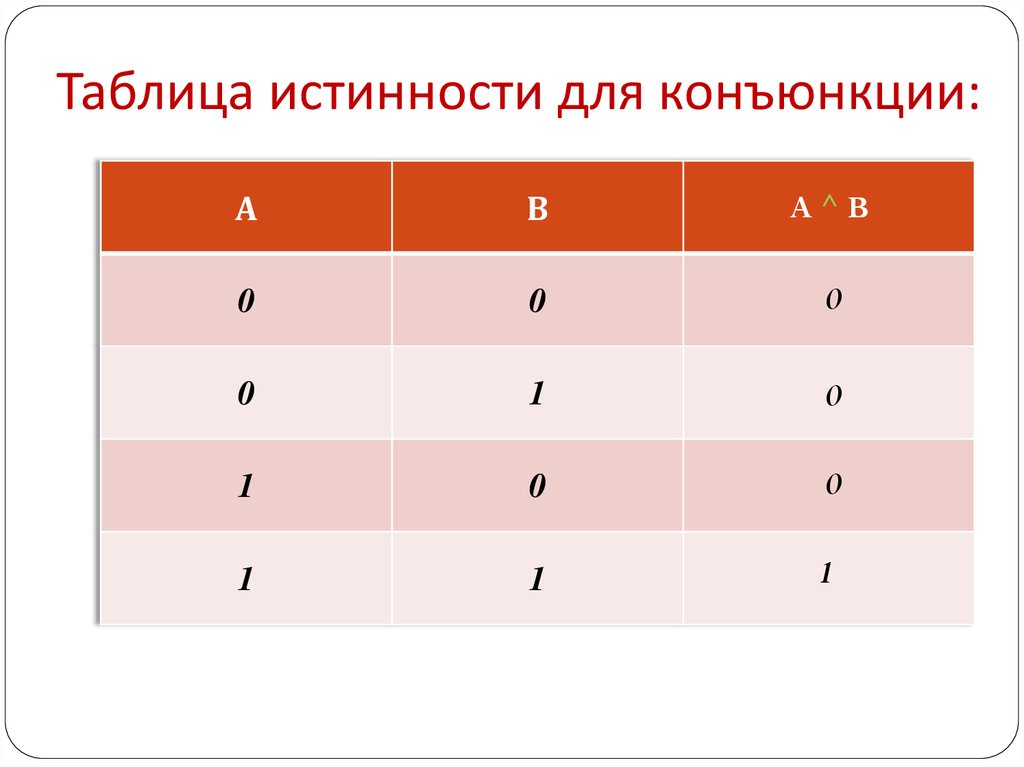
6. Таблица истинности для конъюнкции:
АВ
A^B
0
0
0
0
1
0
1
0
0
1
1
1
7.
2. Дизъюнкция (логическое сложение,v, «ИЛИ») - ставит в соответствие двум
простым логическим выражениям
новое сложное логическое выражение,
которое будет истинным тогда и
только тогда, когда истинно хотя бы
одно из исходных (простых)
логических выражений.
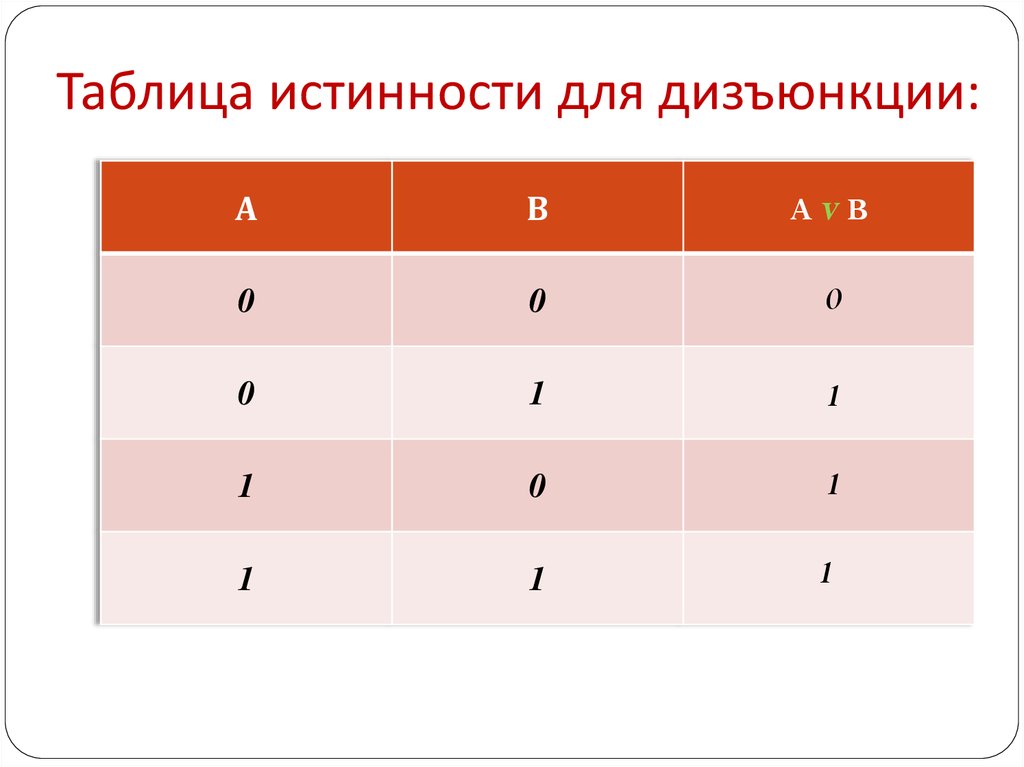
8. Таблица истинности для дизъюнкции:
АВ
AvB
0
0
0
0
1
1
1
0
1
1
1
1
9.
3. Инверсия (отрицание, , «НЕВЕРНО,ЧТО» ) - если исходное выражение
истинно, то результат его отрицания
будет ложным, и наоборот если
исходное выражение ложно, то его
отрицание будет истинным.
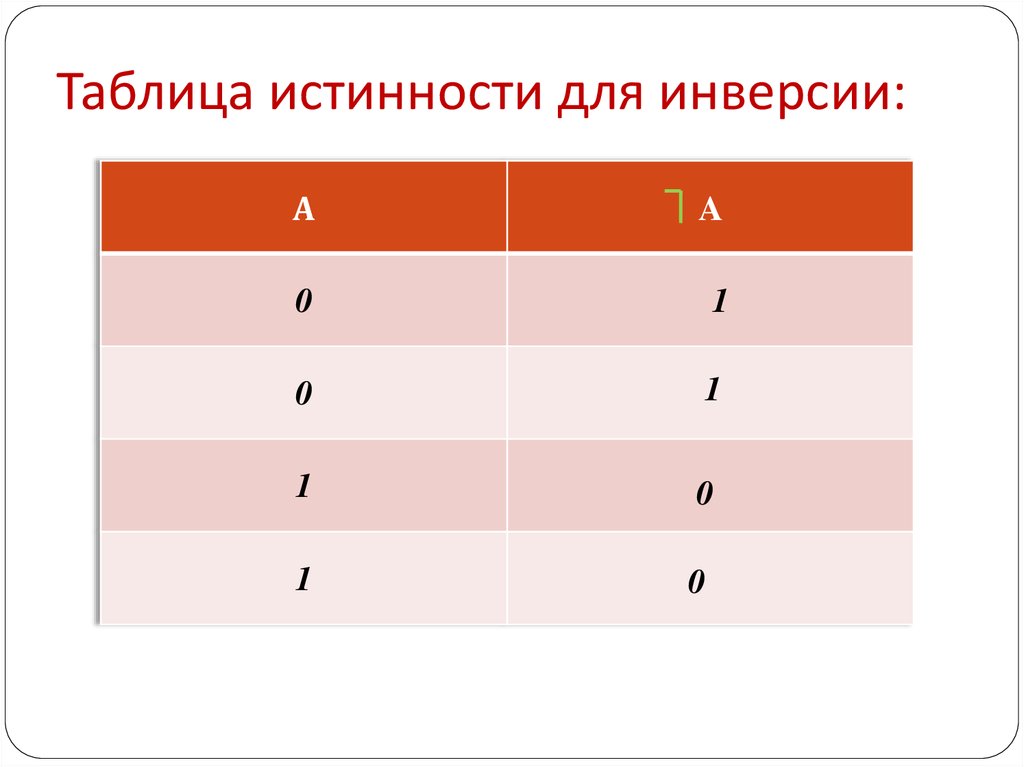
10. Таблица истинности для инверсии:
АA
0
1
0
1
1
0
1
0
11.
4. Импликация (логическоеследование, =>, «если… , то…») – её
результат является ЛОЖЬ тогда и
только тогда, когда условие истинно, а
следствие ложно.
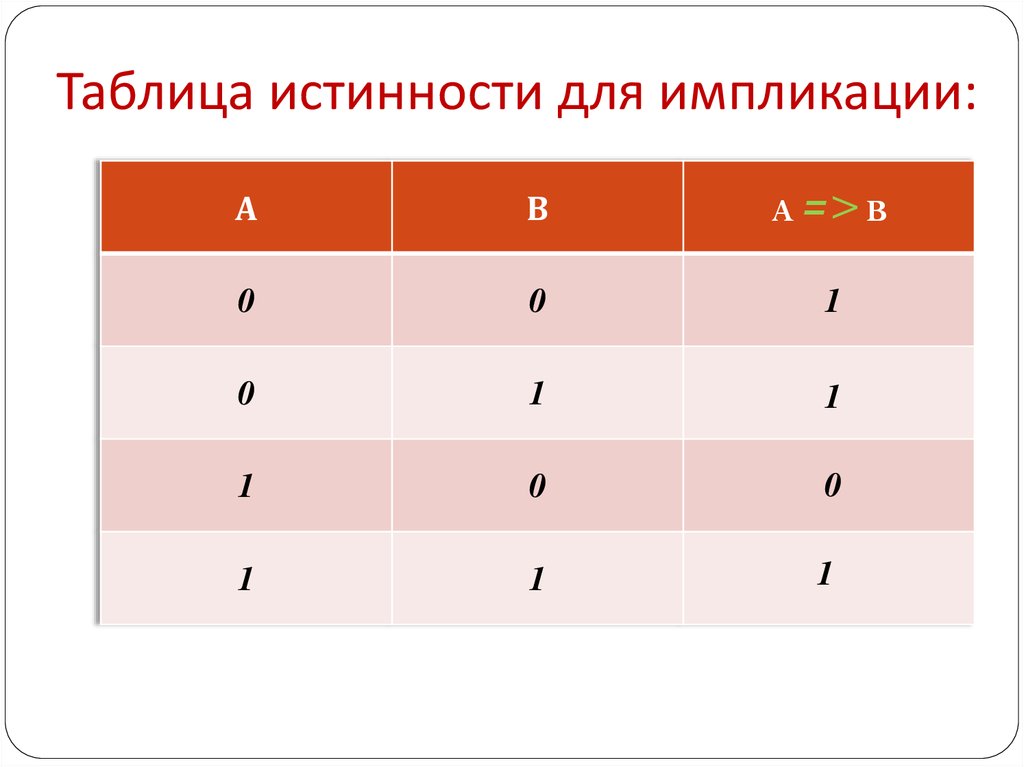
12. Таблица истинности для импликации:
АВ
A => B
0
0
1
0
1
1
1
0
0
1
1
1
13.
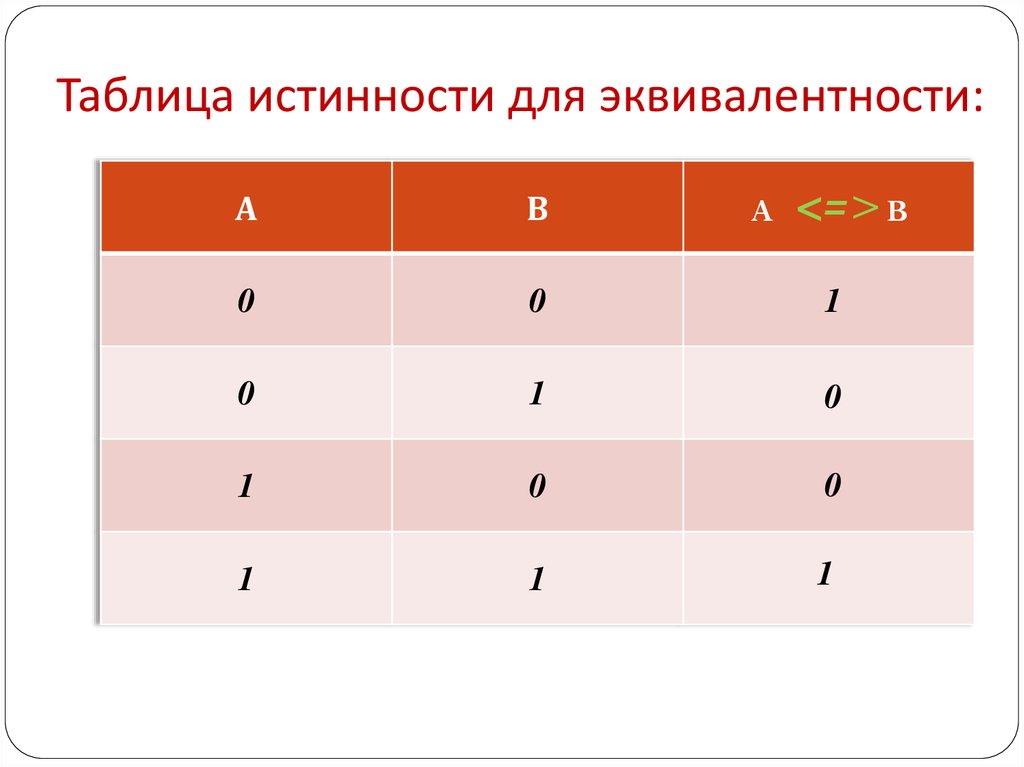
4. Эквивалентность (равнозначность,<=>) - ставит в соответствие двум
простым логическим выражениям новое
сложное логическое выражение, которое
будет истинным тогда и только тогда,
когда оба исходных (простых) выражения
одновременно истинны или ложны.
14. Таблица истинности для эквивалентности:
АВ
0
0
1
0
1
0
1
0
0
1
1
1
A
<=> B
15. Порядок выполнения логических операций в сложном логическом выражении:
1.Конъюнкция (A ^ B)
2.
Дизъюнкция (A V B)
3.
Инверсия (
4.
Импликация (A => B)
5.
Эквивалентность ( A <=> B)
Для изменения указанного порядка выполнения
логических операций используются круглые
скобки.
A)
16. Домашнее задание:
Выучить 5 основных логическихопераций и порядок выполнения
логических операций в сложном
логическом выражении.
17. Определить порядок выполнения логических операций:
1. D=1.
2.
3.
( A v B ^ C)
В ^C
A v В ^C
(A v В ^C)
18.
2. D=A ^ (B v C)
1.
A
2.
3.
(В v C)
A ^ (В v C)
3. D=(A v B) ^ (A => C)
4. D=(A <=> B v C) => B












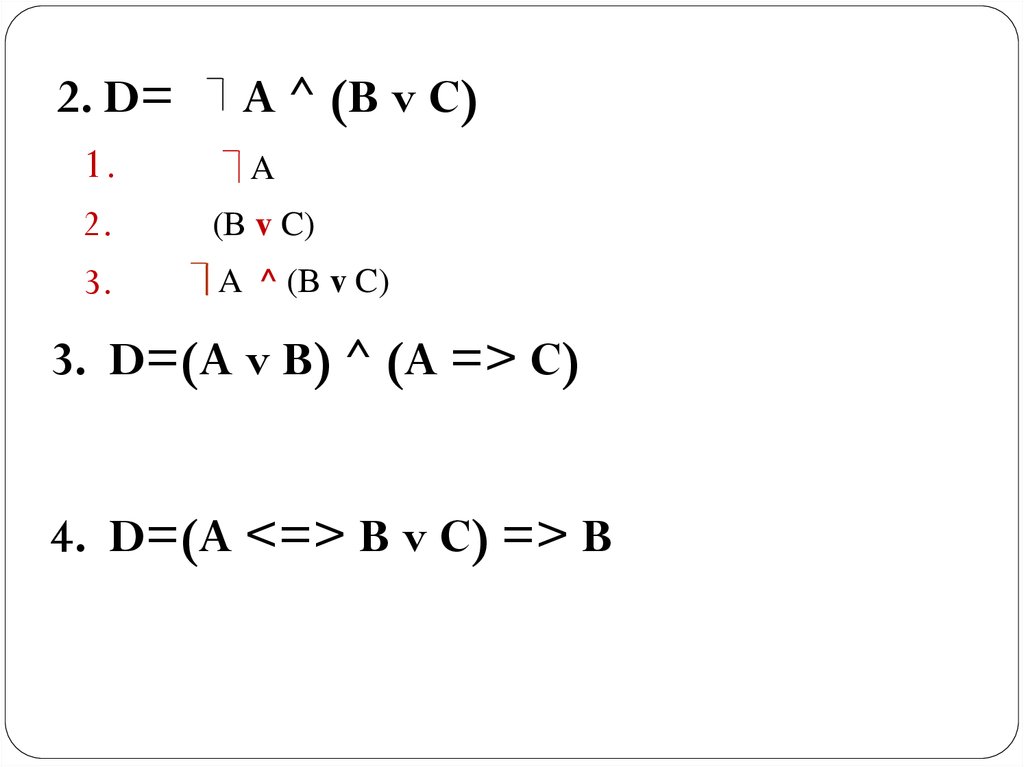
 informatics
informatics








