Similar presentations:
Алгебра высказываний Понятие высказывания. Основные логические операции. Формулы логики
1. Лекция 1-2 Алгебра высказываний
Понятие высказывания.Основные логические операции.
Формулы логики.
Таблица истинности и методика её построения
2. 1. Основные понятия. Понятие высказывания.
Высказываниеэто
повествовательное
предложение, про которое можно определенно
сказать истинно оно или ложно (истина
(логическая 1), ложь (логический 0)).
Высказывания
обозначаются
заглавными
латинскими буквами A,B,..
или буквами с
индексами A1, А2,…
3. Примеры
Следующие предложения являются высказываниями:A1: «Лондон — столица Австрии».
A2: «Число 8 больше числа 3».
A3: «Число 8 больше числа 13».
A4: «Луна — спутник планеты Земля».
Высказывания A1,A3 — ложные, а A2,A4 — истинные.
Следующие предложения не являются высказываниями:
B1: «Какой сегодня день недели?».
B2: «2+3».
B3: «Число x больше 3».
Мы не можем сказать о любом из
высказываний B1,B2,B3 истинно оно или ложно.
4.
Логические операции - действия, результатомкоторых является изменение содержания или
объема понятий, а также образование новых
понятий.
5.
Логическая формула - это запись высказывания,состоящая из логических величин (констант или
переменных),
объединенных
логическими
операциями (связками).
Логическая функция - это функция логических
переменных, которая может принимать только два
значения: 0 или 1.
Сложное логическое выражение - логическое
выражение, состоящее из одного или нескольких
простых логических выражений, соединенных с
помощью логических операций.
6. 2. Основные логические операции
1. Логическое умножение или конъюнкция - этосложное логическое выражение, которое считается
истинным в том и только том случае, когда оба
простых выражения являются истинными, во всех
остальных случаях данное сложенное выражение
ложно.
Обозначение: F = A & B, F = A ˄ B
7.
2. Логическое сложение или дизъюнкция - этосложное логическое выражение, которое истинно,
если хотя бы одно из простых логических
выражений истинно и ложно тогда и только тогда,
когда оба простых логических выражения ложны.
Обозначение: F = A v B.
8.
3. Логическое отрицание или инверсия - этосложное логическое выражение, если исходное
логическое выражение истинно, то результат
отрицания будет ложным, и наоборот, если
исходное логическое выражение ложно, то
результат отрицания будет истинным.
Другими слова, данная операция означает, что к
исходному логическому выражению добавляется
частица НЕ или слова НЕВЕРНО, ЧТО.
Обозначение:
F А
9.
4. Логическое следование или импликация -этосложное логическое выражение, которое истинно
во всех случаях, кроме как из истины следует ложь.
То есть данная логическая операция связывает два
простых логических выражения, из которых
первое является условием (А), а второе (В) является
следствием.
Обозначение: F = A → B.
«A → B» истинно, если из А может следовать B
10.
5.Логическая
равнозначность
или
эквивалентность
- это сложное логическое
выражение, которое является истинным тогда и
только тогда, когда оба простых логических
выражения имеют одинаковую истинность.
Обозначение: F = A ↔ B
«A ↔ B» истинно тогда и только тогда, когда А и B
равны.
11.
6. Операция XOR (исключающие или) – этосложное логическое выражение, которое является
истинным тогда, когда истинно А или B, но не оба
одновременно.
Эту операцию также называют "сложение по
модулю два".
Обозначение: F = A ⊕ B.
12.
7. «Штрих Шеффера» , И–НЕ, также называют«антиконъюнкция» - это сложное логическое
выражение, которое считается ложным в том и
только том случае, когда оба простых выражения
являются истинными, во всех остальных случаях
данное сложенное выражение истинно.
Обозначение: F = A | B =А˄В
13.
8. «Стрелка Пирса», ИЛИ–НЕ такженазывают «антидизъюнкция» - это сложное
логическое выражение, которое ложно, если хотя бы
одно из простых логических выражений истинно и
истинно тогда и только тогда, когда оба простых
логических выражения ложны.
Обозначение: F = A ↓ B= A v B.
14. 3. Таблица истинности и методика её построения
Значения логической функции для разных сочетанийзначений входных переменных обычно задаются
специальной таблицей - называемой таблицей
истинности.
15. Алгоритм построения таблиц истинности для сложных выражений:
1. Определить количество строк:количество строк = 2n + строка для заголовка, где
n - количество простых высказываний.
2. Определить количество столбцов:
количество столбцов = количество переменных +
количество логических операций;
определить количество переменных (простых выражений);
определить количество логических операций и
последовательность их выполнения.
16. Порядок выполнения логических операций в сложном логическом выражении
1.2.
3.
4.
5.
6.
Скобки ()
Инверсия(отрицание)
Конъюнкция ( логическое умножение)
Дизъюнкция (логическое сложение)
Импликация (если…., то)
Эквивалентность (тогда и только тогда)
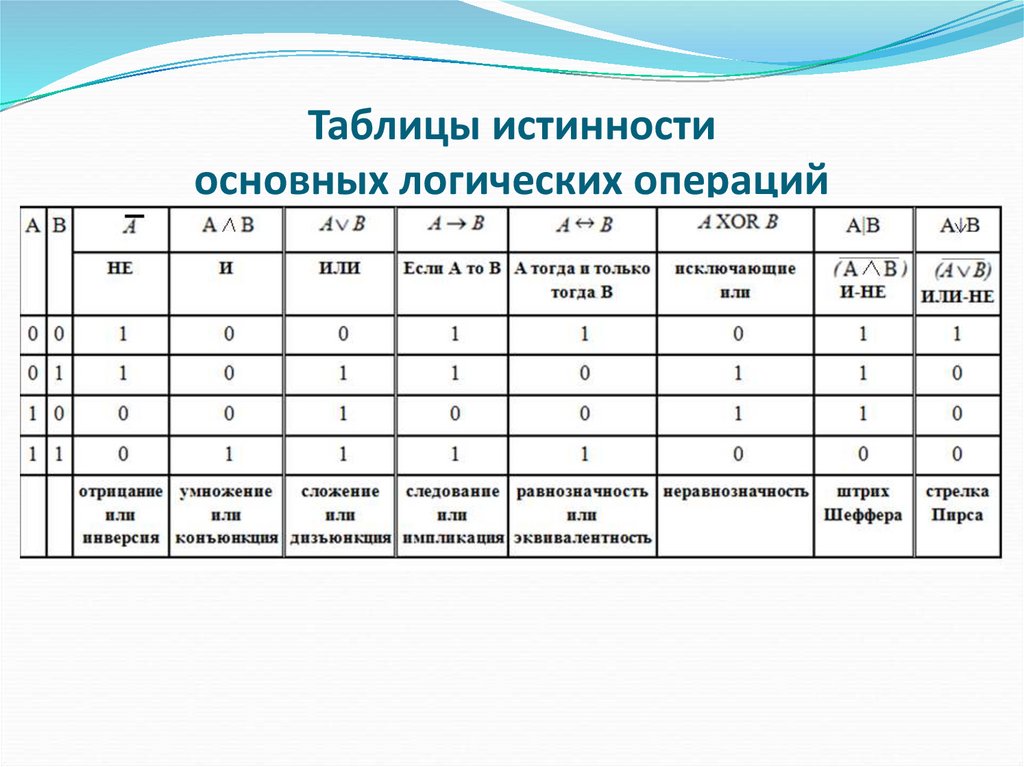
17. Таблицы истинности основных логических операций
18.
Формулу, значения которой для любого наборапеременных есть 1, будем называть тождественно
истинной формулой (или тавтологией).
Формулу, значения которой для любого набора
переменных есть 0, будем называть тождественно
ложной формулой (или противоречием).
19.
Формуланазывается
выполнимой,
если
существует такой набор значений переменных, при
котором эта формула принимает значение 1 .
Формула
называется опровержимой, если
существует такой набор значений переменных, при
котором эта формула принимает значение 0 .
20.
Для доказательства того, что формула являетсятождественно истинной формулой (ТИ),
тождественно ложной формулой (ТЛ),
выполнимой, опровержимой достаточно
построить для данной формулы таблицу
истинности.




















 informatics
informatics








