Определенный интеграл. Формула Ньютона – Лейбница. Замена переменной и интегрирование по частям

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы
Екатерины II
Раздел: Определенный интеграл
Лекция 12. Определенный интеграл.
Формула Ньютона – Лейбница.
Замена переменной
и интегрирование по частям
25.05.2025
г. СанктПетербург
2025
1/16

2.

Содержание лекции
1. Задачи, приводящие к понятию определенного
интеграла (ОИ).
2. Определение ОИ и его геометрический смысл.
3. Основные свойства ОИ
4. Формула Ньютона-Лейбница.
5. Метод подстановки в ОИ.
6. Метод интегрирования по частям в ОИ.
2|16

3.

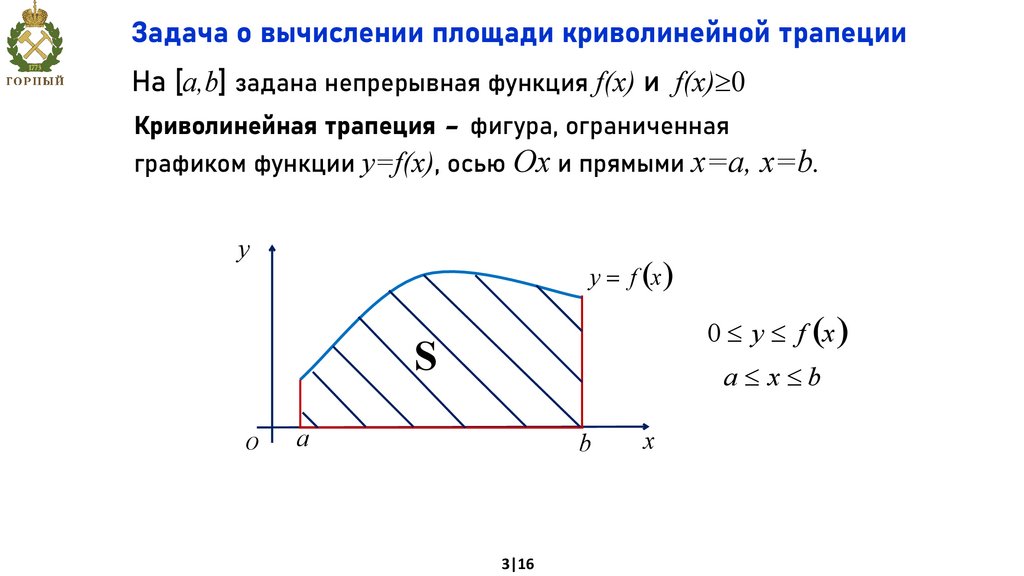
Задача о вычислении площади криволинейной трапеции
На [a,b] задана непрерывная функция f(x) и f(x) 0
Криволинейная трапеция – фигура, ограниченная
графиком функции y=f(x), осью Ох и прямыми х=а, х=b.
y
y = f (x )
0 £ y £ f (x )
S
O
a£ x£b
a
b
3|16
x

4.

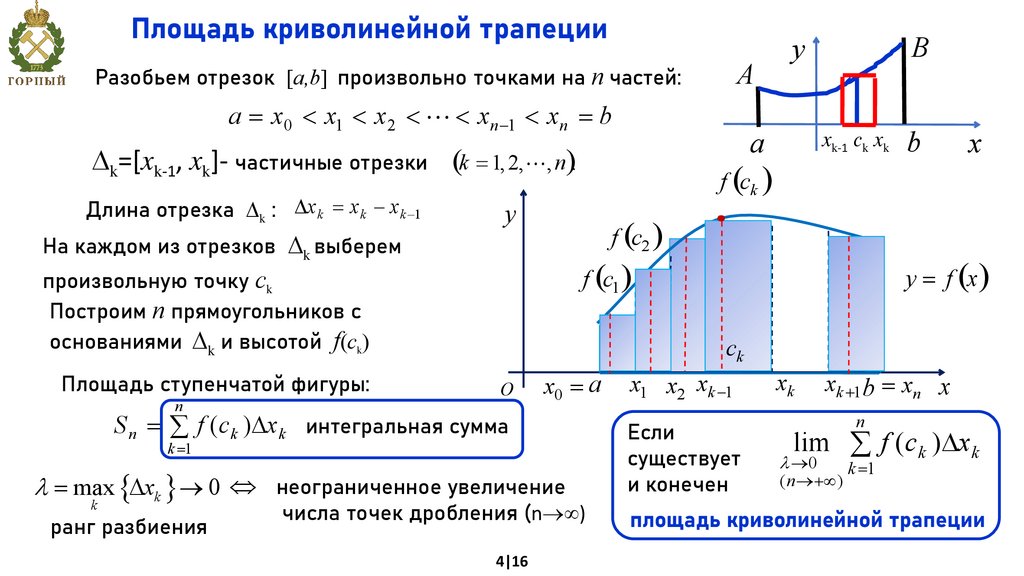
Площадь криволинейной трапеции
А
Разобьем отрезок [a,b] произвольно точками на п частей:
a = x0 < x1 < x 2 < L < x n -1 < x n = b
Длина отрезка k : Dx k = x k - x k -1
f (c2 )
O
x0 = a
k =1
l = max {Dxk }® 0 неограниченное увеличение
ранг разбиения
х
ck
S n = å f (c k )Dx k интегральная сумма
k
b
y = f (x )
f (c1 )
произвольную точку сk
Построим n прямоугольников с
основаниями k и высотой f(сk)
n
f (ck )
y
На каждом из отрезков k выберем
Площадь ступенчатой фигуры:
xk-1 сk xk
а
k=[xk-1, xk]- частичные отрезки (k = 1, 2,L, n ).
B
у
числа точек дробления (n )
4|16
x1 x2 xk -1
Если
существует
и конечен
xk
xk +1b = xn x
n
lim å f (c k )Dx k
l ®0
( n ® +¥ )
k =1
площадь криволинейной трапеции

5.

Опр–е определенного интеграла (ОИ)
1) разбить отрезок a, b точками:
2) ранг разбиения:
l = max{Dxk } k =1, 2, ... , n
функции f (x) на отрезке a, b
a = x0 < x1 < x 2 < L < x n -1 < x n = b
длина отрезка k :
Dx k = x k - x k -1
k
3) выбрать произвольно точку ck k
4) составить интегральную сумму:
n
s n = å f (c k )Dx k
k =1
5) найти предел суммы
при l ® 0 n ® +¥
(конечен, не зависит от способа разбиения
отрезка и от выбора точек ck k )
Теорема. Если функция f (x) кусочнонепрерывна на отрезке a, b , то она
интегрируема на нем.
b
n
a
k =1
f (c k )Dx k
å
ò f ( x)dx = llim
®0
f (x) интегрируема на отрезке a, b
f (x ) – подЫнтегральная функция
5|16

6.

Основные свойства ОИ
Функция f(x) интегрируема на a, b :
b
Геометрический смысл ОИ – площадь
ò f ( x)dx = S
криволинейной трапеции (f(x) 0)
a
1.
ò f ( x)dx = 0
2.
a
3. Свойство аддитивности ОИ
относительно отрезка интегрирования
b
a
a
b
ò f ( x)dx = - ò f ( x)dx
a с
a
b
c
b
a
a
c
ò f (x )dx = ò f (x )dx + ò f (x )dx
b
b
b
a
a
ò a f (x )dx = a ò f (x )dx
4. Свойство однородности ОИ (постоянный
множитель можно выносить за знак интеграла)
5. Свойство аддитивности ОИ относительно подынтегральной функции:
b
b
b
f1(x) и f2(x) интегрируемы на [а, b]
[f1 (x )± f 2 (x )]dx = f1 (x )dx ± f 2 (x )dx
алг. сумма f1(x) f2(x) интегрируема на [а, b]
ò
Замечание. Свойства 4 и 5 –
свойство линейности ОИ
ò
a
b n
n
b
i =1
a
ò å a i fi (x )dx = å a i ò fi (x )dx.
a i =1
6|16
a
ò
a

7.

6. Свойство инвариантности ОИ
относительно переменной интегрирования
b
b
b
a
a
a
ò f (x )dx = ò f (t )dt = ò f (x )dx =L.
æb
ö
ç ò f (x )dx £ 0 ÷
èa
ø
b
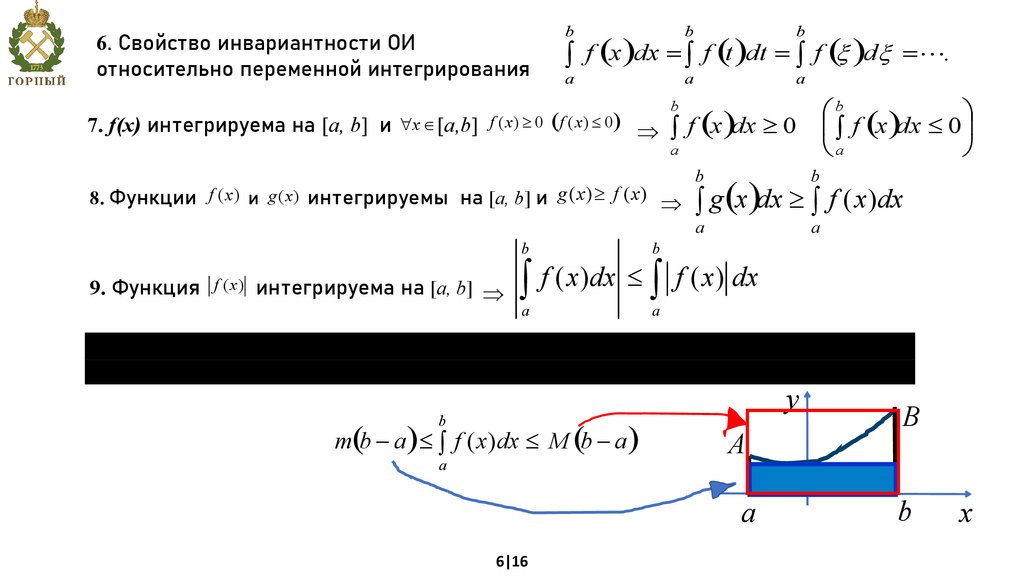
7. f(x) интегрируема на [а, b] и "x Î [а,b] f ( x) ³ 0 ( f ( x) £ 0) ò f (x )dx ³ 0
a
8. Функции f (x) и g (x) интегрируемы на [а, b] и g ( x) ³ f ( x)
9. Функция f ( x) интегрируема на [а, b]
b
b
a
a
b
b
a
a
ò g (x )dx ³ ò f ( x)dx
ò f ( x)dx £ ò f ( x) dx
10. Если на отрезке [a, b] функция f (x) непрерывна, т и М – соответственно
наименьшее и наибольшее значения на отрезке [a, b], то имеет место неравенство:
у
b
m(b - a ) £ ò f ( x)dx £ M (b - a )
a
А
а
6|16
B
b
х

8.

.
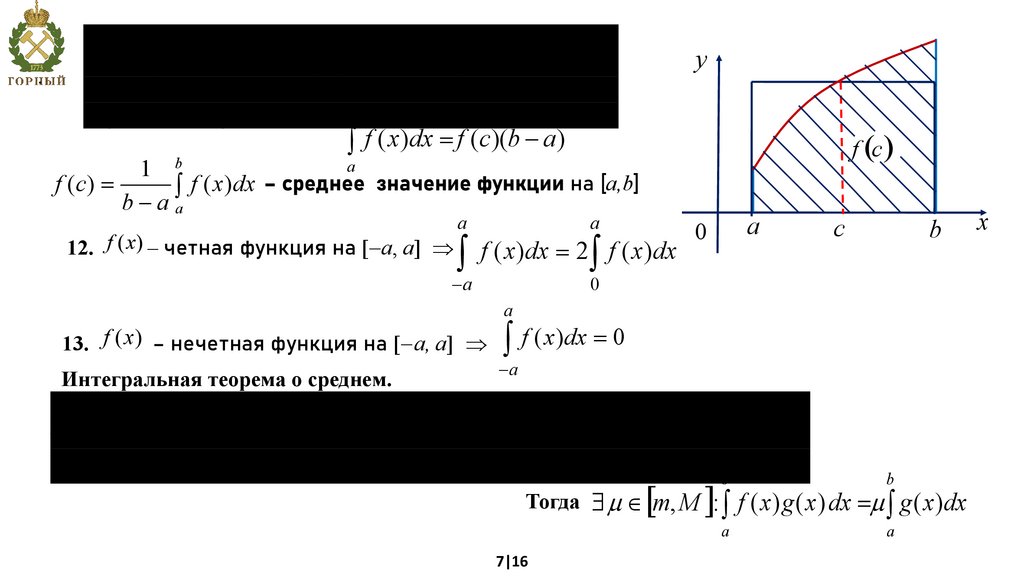
11. (Теорема о среднем).
Если функция f (x) непрерывна на отрезке [a, b], то
найдется хотя бы одна точка c Î [a, b] , что
справедливо равенство b
y
ò f ( x)dx = f (c)(b - a)
f (c )
a
1
f (c ) =
ò f ( x)dx – среднее значение функции на [a,b]
b-aa
b
a
a
-a
0
12. f (x) – четная функция на a, а
ò f ( x)dx = 2ò f ( x)dx
a
0
c
b
a
13. f (x) – нечетная функция на a, а
Интегральная теорема о среднем.
ò f ( x)dx = 0
-a
Пусть функции f(x) и g(x) интегрируемы на отрезке [a, b] и удовлетворяют
условиям: 1) $ m, M :"x Î [a, b]Þ m £ f ( x) £ M ; 2) функция g(x) не меняет знак на
отрезке [a, b], т.е. либо g ( x) ³ 0, "x Î [a, b], либо g ( x) £ 0, "x Î [a, b].
b
[
]
b
Тогда $ m Î m, M : ò f ( x ) g ( x ) dx =m ò g ( x ) dx
a
7|16
a
x

9.

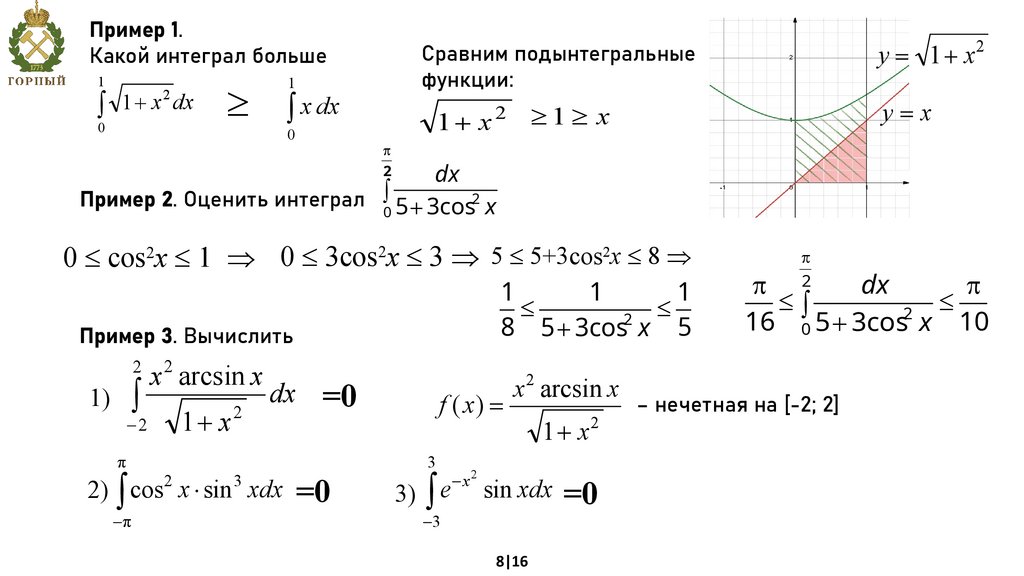
Пример 1.
1
2
ò 1 + x dx
0
1
ò x dx
0
y = 1 + x2
Сравним подынтегральные
функции:
Какой интеграл больше
1+ x
y=x
³1³ x
2
p
2
dx
Пример 2. Оценить интеграл 0ò 5 + 3cos2 x
0 cos2x 1 0 3cos2x 3 5 5+3cos2x 8
1
1
1
£
£
2
8 5 + 3cos x 5
Пример 3. Вычислить
2
ò
1)
2
x arcsin x
1+ x
-2
π
2
dx =0
2) ò cos x × sin xdx =0
-π
2
3
f ( x) =
3
3) ò e
-3
- x2
x 2 arcsin x
1 + x2
sin xdx =0
8|16
p
2
p
dx
p
£ò
£
2
16 0 5 + 3cos x 10
– нечетная на [-2; 2]

10.

Формула Ньютона-Лейбница
f (x) интегрируема на отрезке a, b
a х
b
Теорема Барроу.
Рассмотрим
x
интеграл с
F ( x) = ò f (t )dt
переменным
a
верхним пределом
'
x
Если функция f(x) непрерывна на [a,b], то производная
æ
ö
интеграла с переменным верхним пределом равна
F ¢( x) = çç f (t )dt ÷÷ = f ( x)
значению подынтегральной функции в точке, равной
a
è
øx
верхнему пределу интегрирования:
x + Dx
x
Доказательство:
DF ( x) = F (x + Dx )- F ( x) = ò f (t )dt - ò f (t )dt =
Зафиксируем произвольное значение х a, b
a
a
x
x + Dx
x
придадим ему приращение х 0,
x + Dx
чтобы х+ х a, b
= f (t )dt +
f (t )dt - f (t )dt =
f (t )dt
ò
ò
Применим теорему Лагранжа о среднем:
a
ò
x
ò
a
ò
x
DF ( x) = f (c)Dx DF ( x) = f (c) F ¢( x) = lim DF ( x) = lim f (c) = f ( x)
Dx
c® x
Dx®0 Dx
c Î [ x, x + Dx]
F(x) – первообразная для f (x) на a, b
9|16

11.

Основная теорема интегрального исчисления:
Функция y=f(x) непрерывная на отрезке [a;b],
Ф(х) – любая ее первообразная на этом отрезке
b
ò f ( x)dx = F(b) - F(a)
a
Формула Ньютона-Лейбница
Любые две первообразные F(x) и Ф(х) отличаются друг от друга на некоторую постоянную С:
x
F ( x) = ò f (t )dt = F ( x) + C
При х=а:
a
0 = F(a) + C
При х=b:
C = -F (a)
"x Î [a, b]
x
ò f (t )dt = F ( x) - F (a)
b
a
a
интегрирования
ò f (t )dt = F (b) - F (a) возвращаясь к прежнему обозначению переменной
Замечание. Если функция f(x) имеет на отрезке [a,b] конечное число точек разрыва 1-го рода,
то ОИ вычисляют по свойству аддитивности, т.е. [a,b] разбивают точками разрыва на
частичные отрезки, в каждом из которых функция непрерывна и находят сумму интегралов на
каждом из них.
10|16

12.

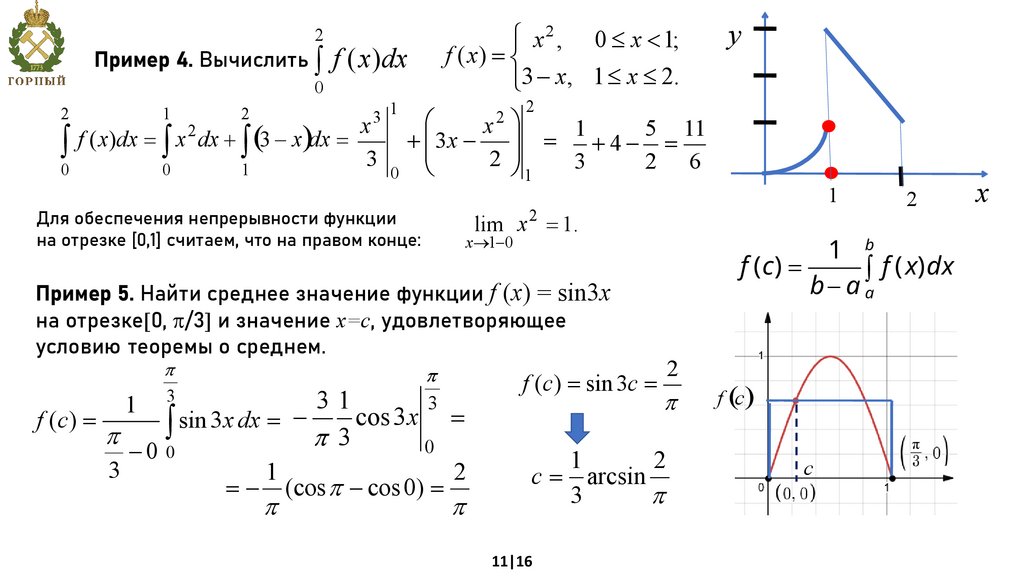
2
Пример 4. Вычислить ò f ( x) dx
0
2
1
3 1
2
x
ò f ( x)dx = ò x dx + ò (3 - x )dx = 3
0
0
1
2
ì x 2 , 0 £ x < 1;
f ( x) = í
î3 - x, 1 £ x £ 2.
2ö
2
æ
x ÷
1
5 11
ç
+ 3x =
+4- =
ç
÷
2 ø
3
2 6
è
0
1
lim x 2 = 1.
Для обеспечения непрерывности функции
на отрезке [0,1] считаем, что на правом конце:
x ®1-0
на отрезке 0, /3 и значение х=с, удовлетворяющее
условию теоремы о среднем.
p
2
p
f (c) = sin 3c =
f (c ) =
p
3
-0
31
3
ò sin 3x dx = - p 3 cos 3x 0 =
0
p
3
=-
1
p
(cos p - cos 0) =
2
p
1
2
c = arcsin
3
p
11|16
1
2
1 b
f ( c) =
ò f ( x) dx
b- a a
Пример 5. Найти среднее значение функции f (x) = sin3x
1
у
f (c )
c
х

13.

Замена переменной в ОИ (метод подстановки)
Теорема. Если функция f(x) непрерывна на отрезке [a, b], а функция j (t ) непрерывно
дифференцируема на отрезке [a , b ], причем отрезок [a , b ]преобразуется функцией j (t )
в отрезок [a, b], так что j (a ) = a, j (b ) = b , то справедлива формула:
b
ò
b
ò [ ( )]j ¢(t )dt.
Док-во. Пусть F(x) − какая-либо первообразная для
f ( x)dx
= f jt
функции f(x) на [a,b].
a
a
x =j (t )
Вычислим производную функции F[ (t)]
¢
по правилу дифференцирования
(F [j (t )]) = F ' [j (t )]j ' (t ) = f [j (t )]j ¢(t ).
сложной функции
F ¢(x ) = f (x )
Функция F[ (t)] первообразная для функции f j t j ¢ t
По формуле НьютонаЛейбница имеем:
С другой стороны:
[ ( )] ( )
b
ò f [j (t )]j ¢(t )dt = F [j (t )]a = F [j (b )]- F [j (a )]= F (b) - F (a).
a
b
b
ò f ( x)dx = F (b) - F (a).
a
12|16

14.

ln 2
Пример 6. Вычислить интеграл
ln 2
ò
0
x
ò
e x - 1 dx.
0
1
e -1 = t Þ x = ln(1 + t ) x = 0 Þ t = 0,
1 2
2t
t +1-1
e - 1 dx =
=
t
×
dt
=
2tdt
2
dt =
2
2
x = ln 2 Þ t = 1
dx =
0 1+ t
2
t +1
0
1
+
t
1
1 ö
æ
1
1
p
æ pö
2 ç1 dt
=
÷
2
t
arctgt
=
2ç1 - ÷ = 2 2
0
0
è 1+ t ø
4
2
x
2
ò
) è
(
ò
0
ò
ø
Формула интегрирования по частям в ОИ
b
Теорема. Если функции u=u(x) и v=v(x) непрерывны вместе со
своими производными на отрезке [a,b], то справедлива формула:
Доказательство.
Вычислим интеграл
По формуле
Ньютона-Лейбница:
b
¢
a
b
b
b
a
a
a
b
uv a
b
uv a =
13|16
b
b
ò vdu + ò udv
a
a
b
ò udv =uv a - ò vdu
(
u ¢v + uv ¢)dx = ò u ¢vdx + ò uv ¢dx
(
)
uv
dx
=
ò
ò
a
b
a

15.

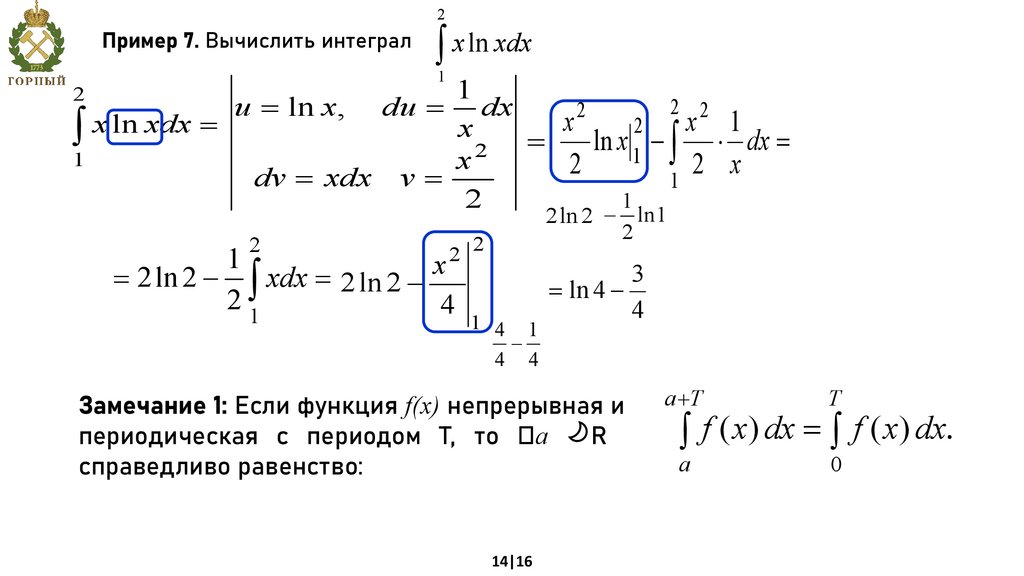
Пример 7. Вычислить интеграл
2
ò x ln xdx
1
1
2 2
u = ln x, du = dx
2
x
x 1
2
x
ò x ln xdx =
=
ln x 1 × dx =
2
1
x
2
2
x
dv = xdx v =
1
2
1
2
ò
2
2 ln 2 - ln 1
2
2 2
1
x
= 2 ln 2 - ò xdx = 2 ln 2 21
4
1 4
4
-
1
4
3
= ln 4 4
Замечание 1: Если функция f(x) непрерывная и
периодическая с периодом Т, то a R
справедливо равенство:
14|16
a +T
T
a
0
ò f ( x) dx = ò f ( x) dx.

16.

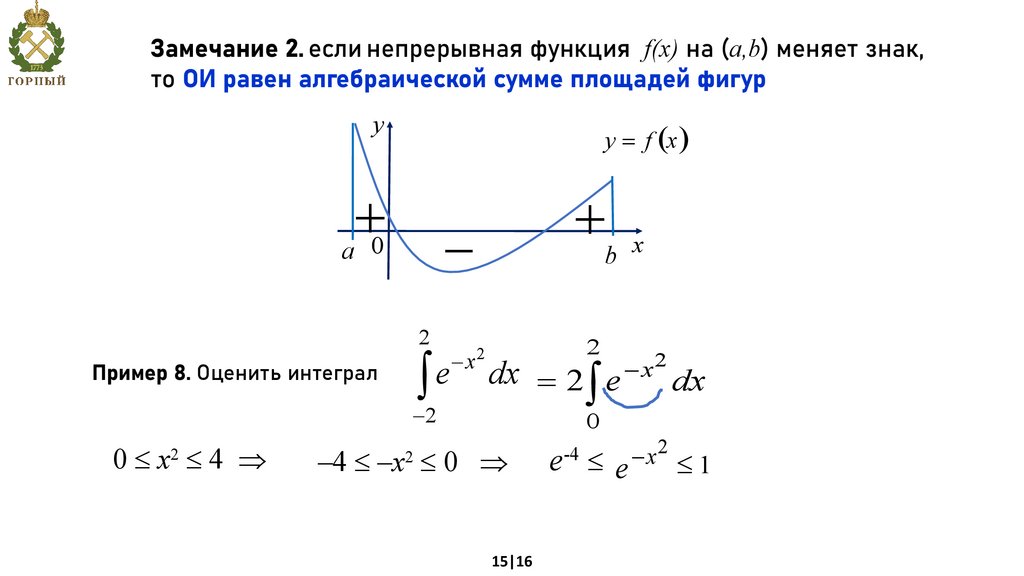
Замечание 2. если непрерывная функция f(x) на (а,b) меняет знак,
то ОИ равен алгебраической сумме площадей фигур
y
y = f (x )
+
a 0
+ x
2
òe
Пример 8. Оценить интеграл
-x
b
2
2
dx = 2 e
ò
-2
0 x 4
2
- x2
dx
0
–4 –x 0
2
15|16
е e
-4
- x2 1

17.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы Екатерины
II
16|16