Теплопередача

1.

ТЕПЛОПЕРЕДАЧА
Теорией теплообмена (теплопередачей), называется
наука изучающая процессы передачи теплоты (теплообмен
между телами) и распределение температуры в твердых,
жидких и газообразных телах.
Различают три основные формы передачи теплоты:
теплопроводность, конвективный теплообмен и лучистый
теплообмен.
Теплопроводностью называется процесс передачи
теплоты путем непосредственного соприкосновения тел
или отдельных частей тела, за счет передачи энергии
движения одних микрочастиц другим.

2.

Конвекция – процесс переноса теплоты при
перемещении объемов жидкости или газа в
пространстве из области одной температуры в область с
другой температурой.
Конвективным теплообменном называется процесс
передачи теплоты, в котором совместно участвуют
теплопроводность и конвекция.

3.

В зависимости от причины вызывающей движение
жидкости, различают конвективный теплообмен при
свободном движении жидкости (свободная конвекция)
и конвективный теплообмен при вынужденном
движении жидкости (вынужденная конвекция).
Свободная конвекция возникает вследствие разности
плотностей неравномерно нагретых слоев жидкости или
газа в поле сил тяготения.
Вынужденная конвекция возникает под влиянием
внешнего воздействия (например, ветра, насоса,
компрессора, вентилятора и т.д.).

4.

Тепловым излучением называется процесс переноса
теплоты в пространстве электромагнитными волнами.
Лучистым теплообменом называется процесс
передачи теплоты излучением между телами, который
включает последовательное превращение внутренней
энергии тела в энергию излучения, распространение ее
в пространстве и превращение энергии излучения во
внутреннюю энергию другого тела.

5.

Основные положения теории теплопроводности
Температурное поле.
В общем случае процесс передачи теплоты
теплопроводностью в твердом теле сопровождается
изменением температуры как, в пространстве, так и во
времени.
Совокупность значений температуры в данный
момент времени для всех точек пространства,
определяемых координатами называется
температурным полем.

6.

Математическим выражением температурного поля
записанное в неявной форме
t f x , y , z ,
Различают стационарное (установившееся) и
нестационарное (неустановившееся) температурные
поля.
Стационарное температурное поле наблюдается в
том случае, когда температура в различных точках
пространства не изменяется во времени. Если
температура изменяется во времени – температурное
поле называется нестационарным.

7.

Температурное поле может быть функцией трех,
двух и одной координаты. Соответственно оно
называется трех-, двух и одномерным.
Простейшее одномерное стационарное
температурное поле
t f(x)

8.

В соответствии с классификацией температурного
поля принципиально различают стационарный и
нестационарный процессы передачи теплоты.
Аналитическое исследование теплопроводности
сводится к изучению пространственно-временного
изменения температуры, т.е. нахождению уравнения
температурного поля в явном виде.

9.

Температурный градиент.
Если соединить точки тела, имеющие одинаковую
температуру, получим поверхность равных температур,
называемую изотермической.
Изотермической поверхностью тела называется
геометрическое место точек, имеющих одинаковую
температуру. Поскольку в одной и той же точке тела
одновременно не может быть двух различных значений
температуры, изотермические поверхности не могут
пересекаться, они либо замыкаются внутри самого тела
либо обрываются на границах тела.

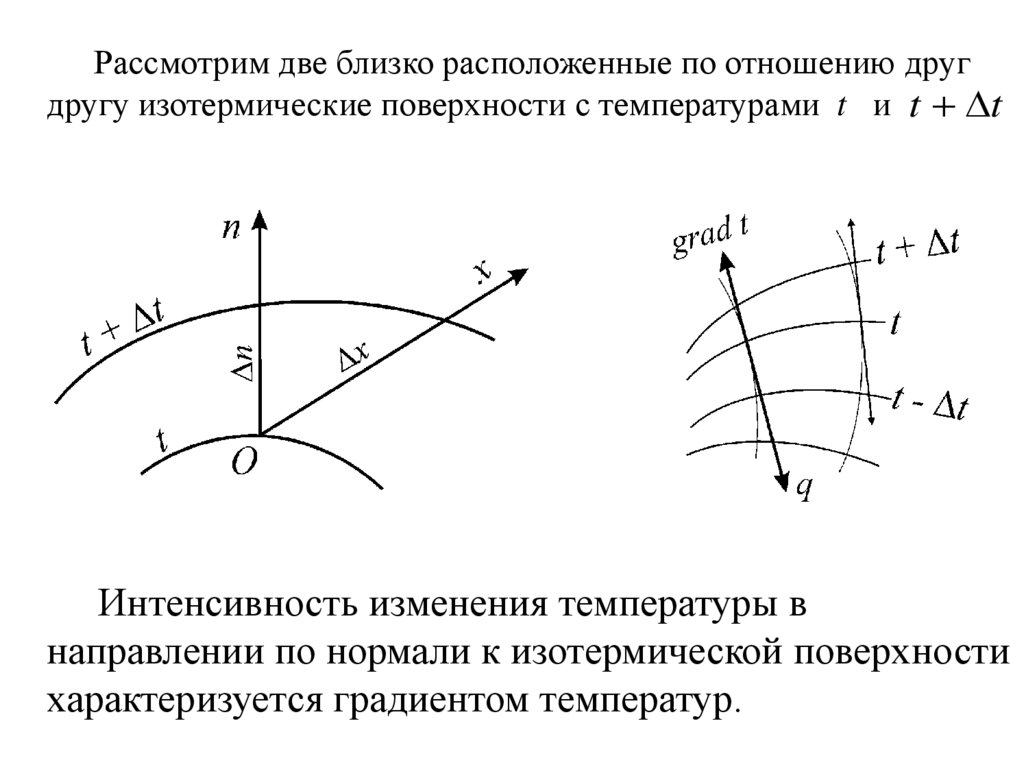
10.

Рассмотрим две близко расположенные по отношению друг
другу изотермические поверхности с температурами t и t t
Интенсивность изменения температуры в
направлении по нормали к изотермической поверхности
характеризуется градиентом температур.

11.

Температурный градиент есть вектор направленный
по нормали к изотермической поверхности в сторону
возрастания температуры и численно равный пределу
отношения изменения температуры к расстоянию
между изотермами по нормали (К/м)
t t
grad t lim
n
n 0 n

12.

В случае трехмерного температурного поля
суммарный температурный градиент определяется по
правилу сложения векторов
gradt igradt x jgradt y kgradt z
i , j ,k – единичные векторы в направлении.

13.

Тепловой поток. Закон Фурье
Согласно гипотезе Фурье количество теплоты
проходящей через элемент изотермической поверхности
за промежуток времени, пропорционально
температурному градиенту
t
Q grad t dF d dF d
n

14.

Количество теплоты, проходящее в единицу времени
через единицу площади изотермической поверхности ,
называется плотностью теплового потока.
q
Q
dF d
Количества теплоты , проходящее в единицу времени
через изотермическую поверхность, называется
тепловым потоком (Дж/с =Вт)
t
Q q dF dF
F
F n

15.

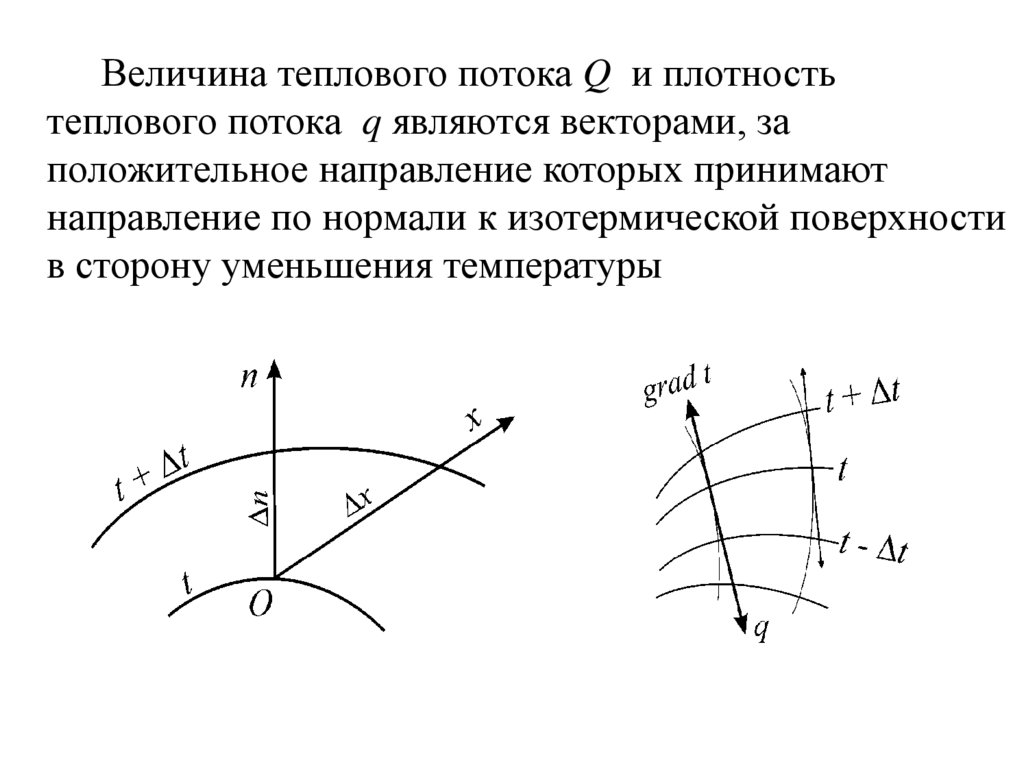
Величина теплового потока Q и плотность
теплового потока q являются векторами, за
положительное направление которых принимают
направление по нормали к изотермической поверхности
в сторону уменьшения температуры

16.

Скалярная величина вектора плотности теплового
потока
t
q
n
Скалярная величина вектора теплового потока
t
Q F
n

17.

Полное количество теплоты, проходящее через
изотермическую поверхность за время
t
Q dFd
0 F n

18.

Выражение плотности тепловых потоков в
направлении осей
t
q x ;
x
t
q z
z
t
q y ;
y
Вектор теплового потока для трехмерной задачи
q iq x jq y kq z

19.

Коэффициент теплопроводности.
Под коэффициентом теплопроводности понимают
тепловой поток, передаваемый через единичную
поверхность при единичном значении температурного
градиента
Q
F gradt

20.

Для каждого тела коэффициент теплопроводности
имеет свое численное значение и, зависит от природы,
пористости, влажности, давления, температуры и
других параметров.
Для многих материалов с достаточной для практики
степенью точности, зависимость коэффициента
теплопроводности от температуры можно принять
линейной
0 1 b ,

21.

Наихудшими проводниками теплоты являются газы.
Коэффициент теплопроводности газов возрастает с
увеличением температуры и изменяется в пределах
0,005 – 0,5 Вт/(м·К).
Коэффициент теплопроводности жидкостей лежит в
пределах 0,07 – 0,7 Вт/(м·К) и, как правило (за
исключением воды и глицерина), уменьшается с
увеличением температуры.
Наилучшими проводниками теплоты являются металлы,
у которых 10 – 420 Вт/(м·К). У большей части металлов
с возрастанием температуры он уменьшается.
Вещества с коэффициентом теплопроводности меньше
0,25 Вт/(м·К) называются теплоизоляционными .

22.

Дифференциальное уравнение теплопроводности
Дифференциальное уравнение теплопроводности
при следующих допущениях:
тело однородно и изотропно;
• физические параметры тела постоянны во времени и
пространстве;
• температурные деформации рассматриваемого
элементарного объема малы по сравнению с самим
объемом;
• внутренние источники теплоты распределены в
рассматриваемом объеме равномерно;
• макрочастицы тела неподвижны относительно друг
друга.

23.

Дифференциальное уравнение теплопроводности
имеет следующий вид:
2
2
2
qv
t
t t t qv
2
a t a 2 2 2
c x y z c

24.

– время, сек;
a
– коэффициент температуропроводности,
c
характеризующий скорость изменения температуры в
любой точке тела, м2 /с;
c – теплоемкость тела , Дж/кг · К ;
– плотность тела , кг/м3;
qv – объемная плотность тепловыделения, Вт/м3;
– оператор Лапласа.

25.

В цилиндрических координатах
2
2
2
t
t 1 t 1 t t qv
a 2
2 2 2
r r r
z c
r
r – радиус вектор;
– угол наклона радиус–вектора.

26.

Условия однозначности или краевые условия:
• геометрические условия (форма, размеры тела);
• физические условия (физические свойства тела и его
физические параметры);
• начальные условия (распределение температуры в теле
в начальный момент времени);
• граничные условия, определяющие взаимодействие тела
с окружающей средой.

27.

1. Граничные условия первого рода.
Задается распределение температуры на поверхности
тела, как функция координат и времени:
t c f x , y , z , ,
t c - температура поверхности тела.
В частном случае, если температура поверхности тела
постоянна
t c const

28.

2. Граничные условия второго рода.
Задается распределение плотности потока на
поверхности тела, как функция координат и времени
qc f x , y , z ,
В частном случае, когда плотность теплового потока на
поверхности тела остается постоянной, имеем
qc q0 const

29.

3. Граничные условия третьего рода.
Задается температура окружающей среды и закон
теплообмена между поверхностью тела и окружающей
средой (закон Ньютона-Рихмана ).
q t c t ж
если
tс t ж
– коэффициент теплоотдачи, представляющий собой
плотность теплового потока подведенного (отведенного)
к единице поверхности тела при разности температур
между поверхностью тела и окружающей среды 1
градус, Вт/м2 К

30.

Количество теплоты, воспринятое поверхностью тела,
распространяется в нем по закону Фурье
t
t c t ж
n c
Отсюда аналитическое выражение граничных условий
третьего рода
t
t с t ж
n c

31.

4. Граничные условия четвертого рода.
Отражают условия теплообмена системы тел имеющих
различные коэффициенты теплопроводности. Между
телами предполагается идеальный контакт.
t1
t2
1 2
n с
n с

32.

Теплопроводность при стационарном режиме
При установившемся (стационарном) тепловом
t
0 , поэтому
режиме
qv
a t
0
c
2
Развернутая форма оператора t зависит от
выбранной системы координат. При отсутствии
внутренних источников теплоты , уравнение
теплопроводности при стационарном температурном
поле запишется в виде 2 t 0
2

33.

Определим тепловой поток теплопроводностью через
изотропную плоскую стенку, предполагая, что
температура меняется только в направлении,
перпендикулярном плоскости стенки
t t
0;
y z
t d t
2 0
2
x
dx
2
2

34.

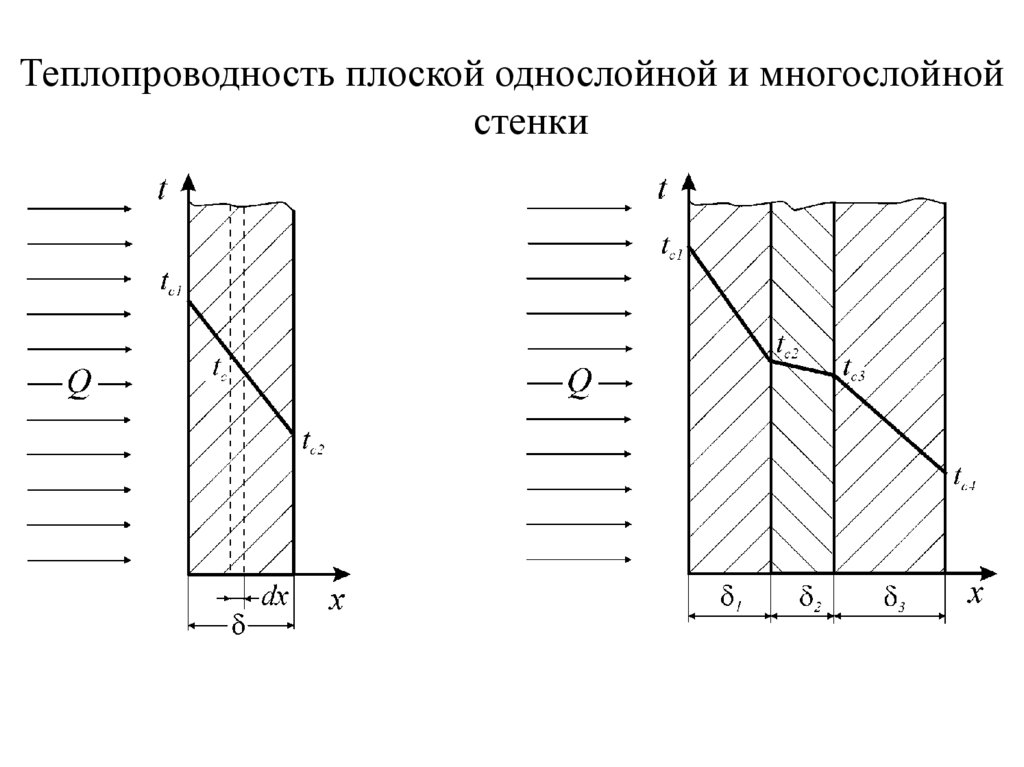
Теплопроводность плоской однослойной и многослойной
стенки

35.

2
d t
0
2
dx
Первое и второе интегрирование данного уравнение
dt
C1 ;
dx
t C1 x C 2
Постоянные интегрирования определяются из
граничных условий первого рода
при
при
x 0 t t c1 ; C 2 t c1
x t tc 2
t c1 t c 2
C1

36.

Подставляя постоянные интегрирования в общее
решение получим закон распределения температуры в
рассматриваемом сечении стенки
t c1 t c 2
t t c1
x
распределение температуры в стенке при граничных
условиях первого рода является линейной функцией.

37.

Расчетное выражение удельного теплового потока
получается из уравнения Фурье
t
q c1 t c1 t c 2
x
С учетом того, что тепловой поток Q qF имеем
Q qF t c1 t c 2 F

38.

Отношение
называется тепловой проводимостью
стенки. Обратная величина
представляет собой
термическое сопротивление стенки.
t с1 t с 2
q
;
Q qF
tс1 tс 2
F

39.

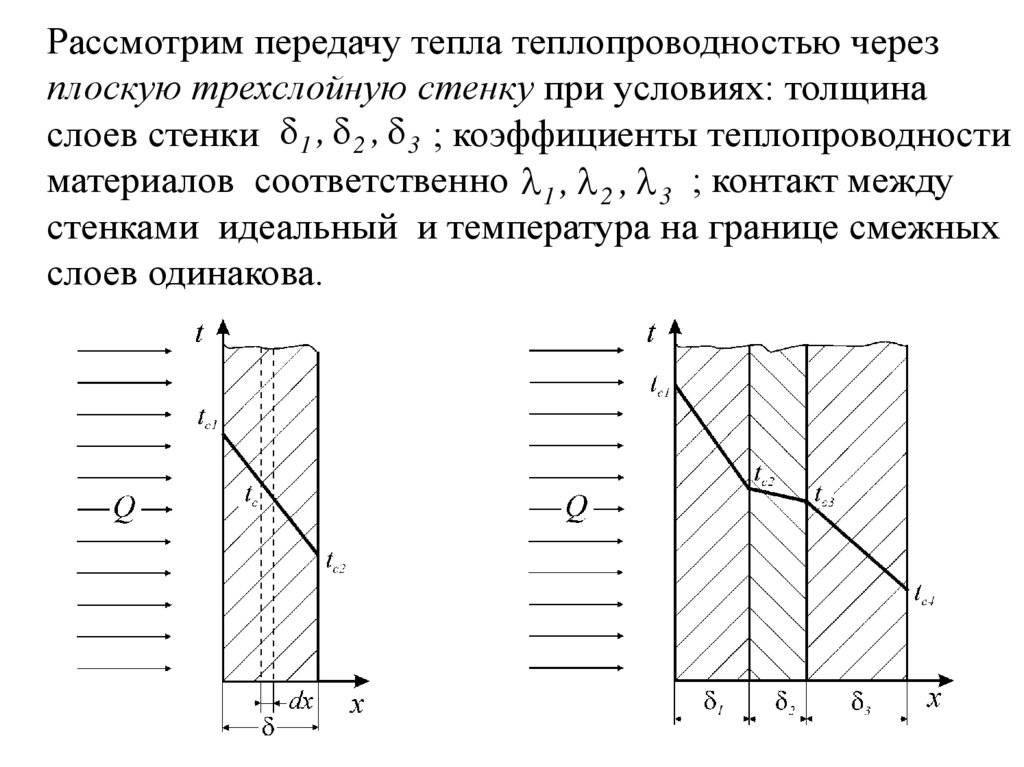
Рассмотрим передачу тепла теплопроводностью через
плоскую трехслойную стенку при условиях: толщина
слоев стенки 1 , 2 , 3 ; коэффициенты теплопроводности
материалов соответственно 1 , 2 , 3 ; контакт между
стенками идеальный и температура на границе смежных
слоев одинакова.

40.

Перенос тепла происходит в стационарных условиях –
плотность теплового потока по всем слоям стенки имеет
одно и то же значение (q=idem).
3
1
2
tc 2 tc 3 tc 3 tc 4 .
q tc1 tc 2
1
2
3

41.

Выделим из этого ряда равенств разности температур
1
t с1 t c 2 q qR1 ;
1
2
tc 2 tc3 q
qR2 ;
2
3
tс 3 tс 4 q qR3 .
3

42.

Складывая левые и правые части уравнений разности
температур, получаем слева изменение температуры в
стенке, справа – произведение плотности теплового
потока q и общего термического сопротивления
1 2 3
tс1 tс 4 q
q R1 R2 R3 .
1 2 3

43.

Плотности теплового потока при переносе тепла
теплопроводностью через плоскую трехслойную стенку
t с1 t с 4
t с1 t с 4
q
,
1 2 3 R1 R2 R3
1 2 3
Q qF

44.

В общем случае для стенки, состоящей из n – слоев
t с 1 t с n 1
t с 1 t с n 1
Q qF
F
F
,
n
n
i
Ri
i 1 i
i 1
t с 1 t с n 1 t с 1 t с n 1 t с 1 t с n 1
q
,
n
n
R
i
Ri
i 1 i
i 1

45.

Температура на стыке двух слоев
i
t i 1 t 1 q
i 1 i
i

46.

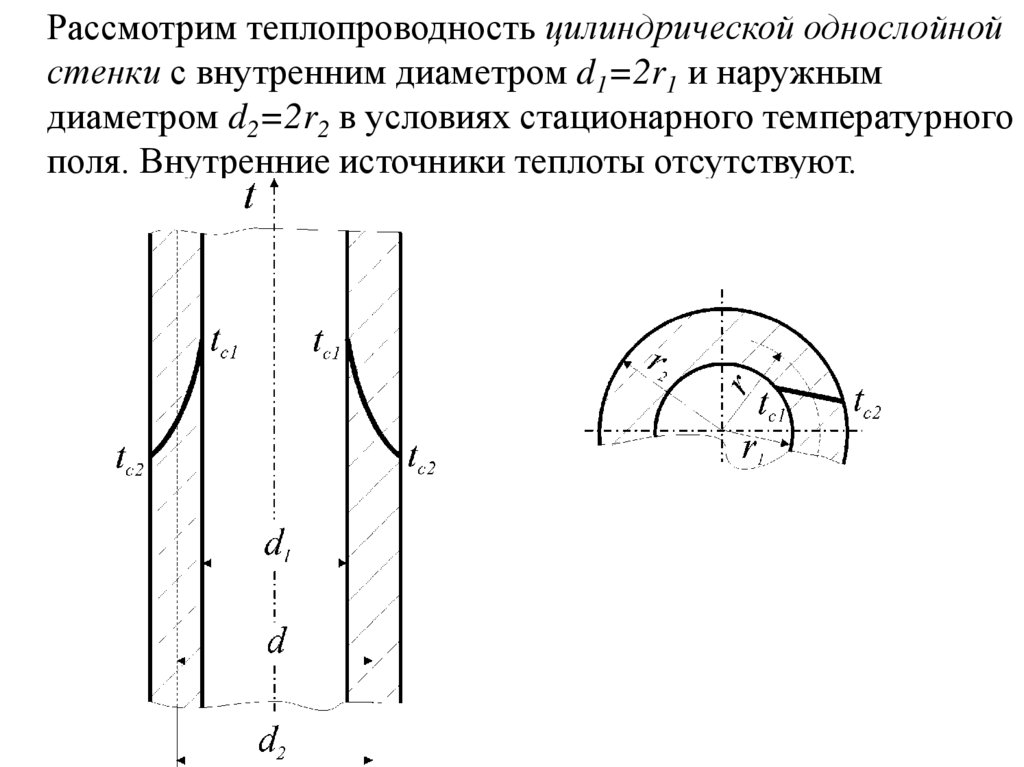
Рассмотрим теплопроводность цилиндрической однослойной
стенки с внутренним диаметром d1=2r1 и наружным
диаметром d2=2r2 в условиях стационарного температурного
поля. Внутренние источники теплоты отсутствуют.

47.

Уравнение теплопроводности цилиндрической стенки
2
2
2
t
t 1 t 1 t t
a 2
2 2 2
r r r
z
r
t
В рассматриваемом случае
0
Температуры на наружной и внутренней поверхности
цилиндрической стенки неизменны и ось z совмещена с
осью цилиндра
2t
2t
0
2
2
z

48.

В рассматриваемом случае температура изменяется
только в радиальном направлении
2
d t 1 dt
0
2
d r r dr
Граничные условия: r r1
r r2
t t с1
t tс 2
dt
введем новую переменную u
dr
du u
0
dr r
тогда

49.

интегрируя
ln u ln r ln C1
потенцируя и переходя к первоначальным переменным,
получаем
dr
dt C1
r
После интегрирования имеем
t C1 ln r C 2

50.

Постоянные С1 и С2 определяются из граничных
условий
t c1 C1 ln r1 C 2
t c 2 C 2 ln r2 C 2

51.

Подставляя полученные значения С1 и С2 в общее
уравнение
t c1 t c 2
С1
r1
ln
r2
получим
ln r1
С2 t c1 t c1 t c 2
r1
ln
r2
r
ln
r1
t t c1 t c1 t c 2
r2
ln
r1

52.

Для определения теплового потока через
цилиндрическую поверхность воспользуемся законом
Фурье
t
Q F ;
r
t
Q 2 rL
r

53.

Подставляя в уравнение Фурье значение градиента
температуры
dt С1
dr r
получим
2 l t c1 t c 2
Q
r2
ln
r1
2 l t c1 t c 2
или Q
d2
ln
d1

54.

Тепловой поток может быть отнесен либо к единице
длины, либо к единице внутренней или внешней
поверхности.
внутренней поверхности
наружной поверхности
t c1 t c 2
Q
q1
1 d2
d 1l
d 1 ln
2 d 1
t c1 t c 2
Q
q1
1 d2
d 2 l
d2
ln
2 d 1

55.

Тепловой поток отнесенный к единице длины, имеет
размерность Вт/м и называется линейной плотностью
теплового потока.
t c1 t c 2
Q
ql
1 d2
l
ln
2 d 1

56.

Рассуждая аналогично, как при получении расчетного
соотношения теплового потока для многослойной
плоской стенки, можно получить выражение для
определения линейной плотности теплового потока в
случае многослойной цилиндрической стенки
t c1 t c n 1
ql i n
d i 1
1
2 ln d
i 1
i
i
i n
1
d i 1
2 ln d называется полным термическим
i 1
i
i
сопротивлением теплопроводности многослойной
цилиндрической стенки.

57.

Температура на границе любых двух слоев:
i
ql
d i 1
1
tc (i 1) tc1
ln
i 1 2 i
di

58.

Обобщенное уравнение стационарной
теплопроводности
При передаче тепла через произвольные криволинейные
стенки тепловой поток определяется по такому же
уравнению, как и для плоской стенки, только в
выражение вводится расчетная поверхность
теплопроводности
Q Fm t1 t 2 .

59.

Расчетная поверхность теплопроводности принимается
в зависимости от вида стенки, через которую
происходит передача тепла:
• Для плоской стенки
Fm F1 F2 F3 ;
• Для цилиндрической стенки
Fm FmL F2 F1 ln F2 F1 ;
• Для сферической стенки
Fm FmG F1 F2 .

60.

Теплопроводность через многослойные криволинейные
стенки определяется по уравнению аналогичному
уравнению теплопроводности плоской многослойной
стенки
t с1 t с n 1
Q n
i
F
i 1 i mi
i , i , Fmi – толщина, коэффициент теплопроводности
и расчетная поверхность рассматриваемого слоя.