Теория теплообмена

1. ТЕОРИЯ ТЕПЛООБМЕНА

2.

•Теоретическими
основами
теплотехники
являются термодинамика и теплопередача фундаментальные базовые дисциплины для
большинства инженерных специальностей.
•Теплопередача (теория теплообмена) – наука,
изучающая процессы передачи теплоты между
телами, распространение теплоты в пространстве
и распределение температуры в телах.
•Представление
и
обсуждение
основных
положений, понятий, законов и расчетных
соотношений
теории
теплообмена
и
их
использование в технологических процессах
нефтяной и газовой промышленности составляют
содержание теплопередачи (теория теплообмена).

3.

Знание законов теплообмена позволяет определить
количество передаваемой теплоты, температурные поля
рассматриваемых систем, интенсифицировать теплообмен
в одних случаях и затруднить его в других, правильно
конструировать и оптимально эксплуатировать машины,
аппараты и другие технические устройства, в которых
рабочие процессы сопровождаются теплообменом.
Самопроизвольный необратимый процесс передачи
теплоты внутри термодинамических систем или между
термодинамическими
системами,
обусловленный
неоднородным распределением температуры, называется
теплообменом. Процессы передачи теплоты представляют
собой процессы обмена внутренней энергией между
элементами
термодинамической
системы
или
термодинамическими системами в форме теплоты. Теория
теплообмена изучает процессы передачи теплоты между
телами или частями тела.

4. Формы передачи теплоты

теплопроводность
конвективный теплообмен
лучистый теплообмен
Теплопроводность представляет собой форму передачи теплоты
путем непосредственного соприкосновения тел или отдельных
частей тела, имеющих различную температуру. При этом процесс
теплообмена
происходит
вследствие
передачи
энергии
микродвижения одних элементарных частиц другим.
Конвективным теплообменом называется форма передачи
теплоты в пространстве, осуществляемая при перемещении
макрочастиц жидкости или газа. При перемещении в пространстве
потоков различно нагретых частиц жидкости или газа происходит
непосредственное их соприкосновение, поэтому здесь имеет место
теплопроводность. Следовательно, конвективный теплообмен
представляет собой совокупное действие двух процессов –
конвекции и теплопроводности.

5.

В зависимости от причины, вызывающей движение
жидкости, различают конвективный теплообмен при
свободном
движении
(свободная
конвекция)
и
конвективный теплообмен при вынужденном движении
жидкости (вынужденная конвекция).
Свободная конвекция возникает вследствие разности плотностей неравномерно нагретых слоев жидкости или газа в
поле сил тяготения. Возникновение и интенсивность свободной конвекции зависит от разности температур, рода и физических свойств жидкости, формы, размеров и положения
тела, а также объема пространства, в котором протекает
процесс.
Вынужденная конвекция возникает под влиянием внешнего воздействия (например, ветра, насоса, компрессора,
вентилятора и т.д.), которое создает перепад давления.
Интенсивность процесса зависит от рода и физических
свойств среды, ее температуры, скорости движения, формы
и размеров пространства, в котором происходит движение.

6.

Тепловым излучением называется процесс
переноса энергии в пространстве электромагнитными волнами.
Лучистым теплообменом называется форма
передачи теплоты излучением между телами,
которая включает последовательное превращение внутренней энергии одного тела в энергию
излучения, распространение ее в пространстве
и превращение энергии излучения во внутреннюю энергию другого тела.
Рассмотренные формы передачи теплоты во
многих случаях осуществляются совместно, что
необходимо учитывать при расчете теплообмена в технологических процессах нефтяной и
газовой промышленности.

7. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ТЕПЛООБМЕНА

Температурное
поле
совокупность
значений
температуры t в данный момент времени для всех
точек пространства, определяемых координатами x , y , z
t f x , y , z ,
стационарное (установившееся)
нестационарное (неустановившееся)
t f
o одномерное
o двухмерное
o трехмерное
Уравнение одномерного стационарного температурного поля
t f(x)
Аналитическое исследование теплообмена сводится, как
правило,
к
определению
пространственно-временного
изменения температуры в исследуемой системе, т.е.
нахождению уравнения температурного поля в явном виде.

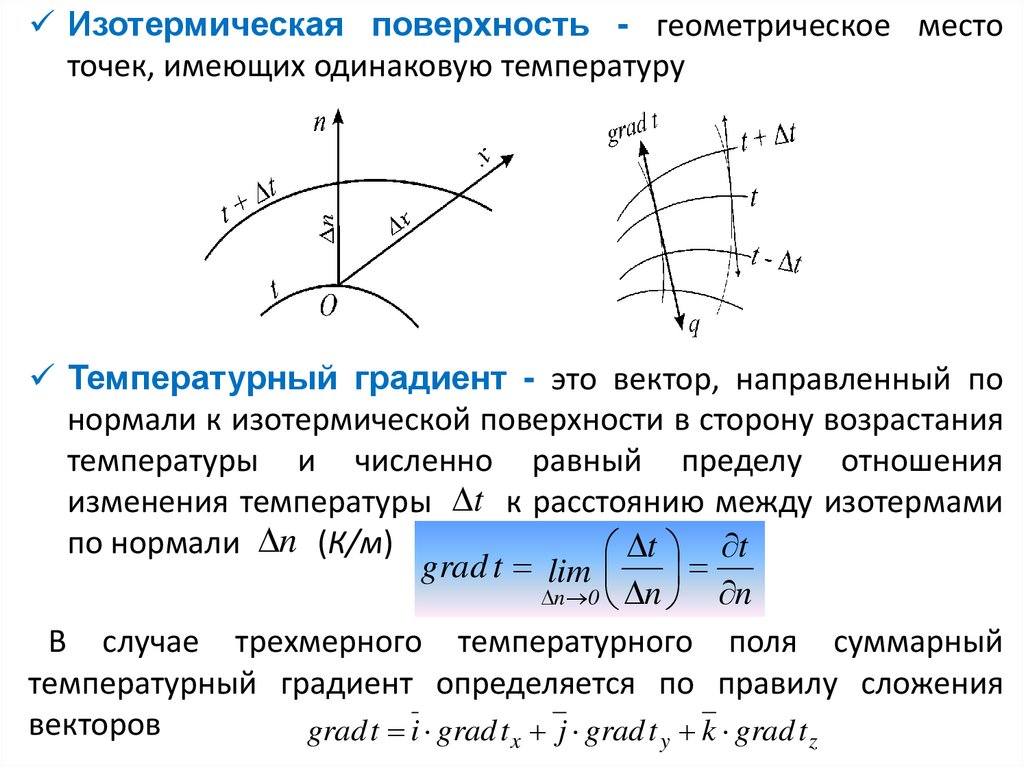
8.

Изотермическая поверхность - геометрическое место
точек, имеющих одинаковую температуру
Температурный градиент - это вектор, направленный по
нормали к изотермической поверхности в сторону возрастания
температуры и численно равный пределу отношения
изменения температуры t к расстоянию между изотермами
по нормали n (К/м)
t t
grad t lim
n
n 0 n
В случае трехмерного температурного поля суммарный
температурный градиент определяется по правилу сложения
векторов
grad t i grad t x j grad t y k grad t z

9.

Тепловой поток (Q, Вт) - количество теплоты Q
,
проходящее в единицу времени через изотермическую
поверхность F
Q
Q
d
Удельный тепловой поток или плотностью теплового
потока – тепловой поток, проходящий через единицу
площади изотермической поверхности
Q
q
dF d
Q q dF
F
Тепловой поток Q, а также плотность теплового потока q
являются векторами, за положительное направление
которых принимается направление по нормали к
изотермической поверхности в сторону уменьшения

10. Теплопроводность при стационарном температурном поле

Теплопроводность представляет собой форму передачи теплоты
путем непосредственного соприкосновения тел или отдельных частей
тела, имеющих различную температуру. При этом процесс теплообмена
происходит вследствие передачи энергии микродвижения одних
элементарных частиц другим.
В чистом виде теплопроводность наблюдается в твердых телах, а
также в тонких прослойках жидкости и газа при отсутствии в них
движения.
В металлах перенос теплоты осуществляется путем движения
(диффузии) свободных электронов, а передача теплоты за счет упругих
колебаний кристаллической решетки второстепенна.
В жидкостях и твердых телах – диэлектриках теплопроводность
осуществляется упругими волнами.
В газах распространение теплоты теплопроводностью происходит
вследствие обмена энергией при соударении молекул и атомов,
имеющих различную скорость теплового движения (путем диффузии
молекул и атомов).

11. Закон Фурье

Количество теплоты, проходящей через элемент
изотермической поверхности dF за промежуток времени d , пропорционально температурному градиенту
t
Q grad t dF d dF d
n
Тепловой поток согласно закону Фурье
t
Q q dF dF
n
F
F
Скалярная составляющая вектора теплового потока
t
Q F
n
Скалярная составляющая вектора плотности теплового
потока
t
q
n

12.

Количество теплоты
t
Q dF d
n
0F
Составляющие плотности теплового потока в направлении
осей x , y , z
t
q x
x
t
q y
y
t
q z
z
Вектор теплового потока для трехмерного температурного
поля
q i qx j q y k qz

13.

Коэффициент теплопроводности - тепловой поток,
передаваемый через единичную площадь поверхности при
единичном значении температурного градиента
Q
F grad t
Коэффициент теплопроводности для каждого тела имеет
свое численное значение и зависит от природы тела,
пористости, влажности, давления, температуры и других
параметров.
С достаточной для практики степенью точности,
зависимость
коэффициента
теплопроводности
от
температуры для многих материалов можно принять
линейной
во всем рассматриваемом интервале
температур
0 1 b t ,

14.

Наихудшими проводниками теплоты являются газы.
Коэффициент теплопроводности газов возрастает с
увеличением температуры и изменяется в пределах
0,005 ÷ 0,5 Вт/(м·К).
Коэффициент теплопроводности жидкостей лежит в
пределах 0,07 ÷ 0,7 Вт/(м·К) и, как правило (за
исключением воды и глицерина), уменьшается с
увеличением температуры.
Наилучшими проводниками теплоты являются металлы,
у которых коэффициент теплопроводности изменяется в
диапазоне 10 420 Вт/(м·К). У большей части
чистых металлов с возрастанием температуры он
уменьшается.

15. Дифференциальное уравнение теплопроводности

Распределение температуры в теле описывается
дифференциальным уравнением теплопроводности. При
условиях, что тело однородно и изотропно, физические
параметры тела постоянны во времени и пространстве,
температурные
деформации
рассматриваемого
элементарного объема малы по сравнению с самим
объемом, внутренние источники теплоты распределены в
рассматриваемом объеме равномерно, макрочастицы тела
неподвижны относительно друг друга, дифференциальное
уравнение теплопроводности имеет следующий вид:
a
qv
t
2t 2t 2t
qv
2
a t
a 2 2 2
cp
c
x
y
z
p
- коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела, м2/c;
qv – объемная плотность внутренних источников теплоты, Bm/м3;
– оператор Лапласа.
cp

16. Условия однозначности

Чтобы
получить
конкретное
решение
дифференциального уравнения теплопроводности (как
и других дифференциальных
уравнений ) для
рассматриваемого
случая,
необходимо
описать
особенности
данного
конкретного
процесса
теплопроводности.
Эти
частные
особенности
называются условиями однозначности, включающими:
геометрические условия (форма, размеры тела);
физические условия (физические свойства тела и его
параметры);
начальные условия (распределение температуры в
теле в начальный момент времени);
граничные условия, определяющие взаимодействие
тела с окружающей средой.

17. Граничные условия

Граничные
условия
первого
рода.
Задается
распределение температуры на поверхности тела, как
функция координат и времени
t c f x , y , z , ,
где t c - температура поверхности тела.
В частном случае, если температура поверхности тела
постоянна, приведенное выражение принимает вид
t c idem .
Граничные условия второго рода. Задается
распределение плотности теплового потока на
поверхности тела, как функция координат и времени
qc f x , y , z ,
В частном случае, когда плотность теплового потока на
поверхности тела остается постоянной, имеем qc q0 idem.

18.

Граничные условия третьего рода. Задается
tж
температура окружающей среды
и закон
теплообмена между поверхностью тела и окружающей
средой (уравнение Ньютона-Рихмана)
q t c t ж если t с t ж ,
где – коэффициент теплоотдачи, Вm/(м2·К).
Тепловой поток, подведенный к поверхности тела,
распространяется в теле по закону Фурье. Следовательно,
t
t c t ж
n c
t
где n – температурный градиент у поверхности тела.
c
Это выражение можно записать в виде
t
t с t ж
n c
Данное уравнение является аналитическим выражением
граничных условий третьего рода.

19.

Граничные условия четвертого рода. Отражают
условия теплообмена между телами, имеющими
идеальный
контакт
и
различные
значения
коэффициентов
теплопроводности.
При
этих
условиях и постоянном тепловом потоке, выражение
граничных
условий
четвертого
рода
можно
представить в виде
t1
t 2
1 2
n с
n c
где 1 , 2 – коэффициенты теплопроводности первого
и второго тела, соответственно.

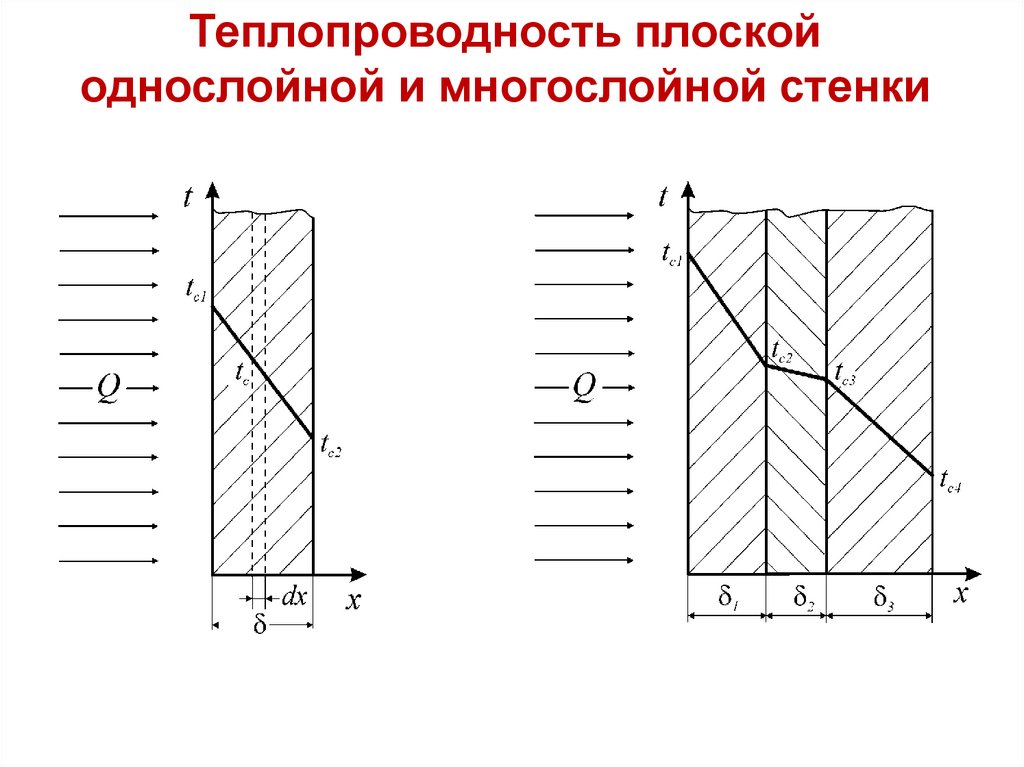
20. Теплопроводность плоской однослойной и многослойной стенки

21.

Рассмотрим дифференциальное уравнение теплопроводности
2
2
2
q
t
qv
t
t
t
2
v
a t
a 2 2 2
cp
y
z c p
x
t
0
t t
0
y z
для одномерного
стационарного
температурного поля при отсутствии внутренних источников
теплоты qv 0 примет вид
2t d 2t
2 0
2
x
dx
dt
C1
В результате интегрирования получаем
dx
t C1 x C2
а после второго интегрирования имеем
(а)
(б)
Постоянные интегрирования определяются из граничных
условий первого рода:
при
x 0 , t t c1 , C 2 t c1 ,
при
x , t tc 2 ,
t c1 t c 2
C1
.

22.

Подставляя постоянные интегрирования в соотношение
(б), получим уравнение распределения температуры в
плоской стенке
t c1 t c 2
t t c1
x
Из этого выражения следует, что температура в плоской
стенке изменяется по линейному закону.
Из закона Фурье, с учетом соотношения (а), получаем
уравнение теплопроводности через однослойную плоскую
стенку
q tc1 tc 2
Q q F
tc1 tc 2 F
- тепловая проводимость и удельное
где ,
термическое сопротивление плоской стенки.
Иная форма представления уравнения теплопроводности
через однослойную плоскую стенку t t
q с 1 с 2 . Q q F t с1 t с 2
F

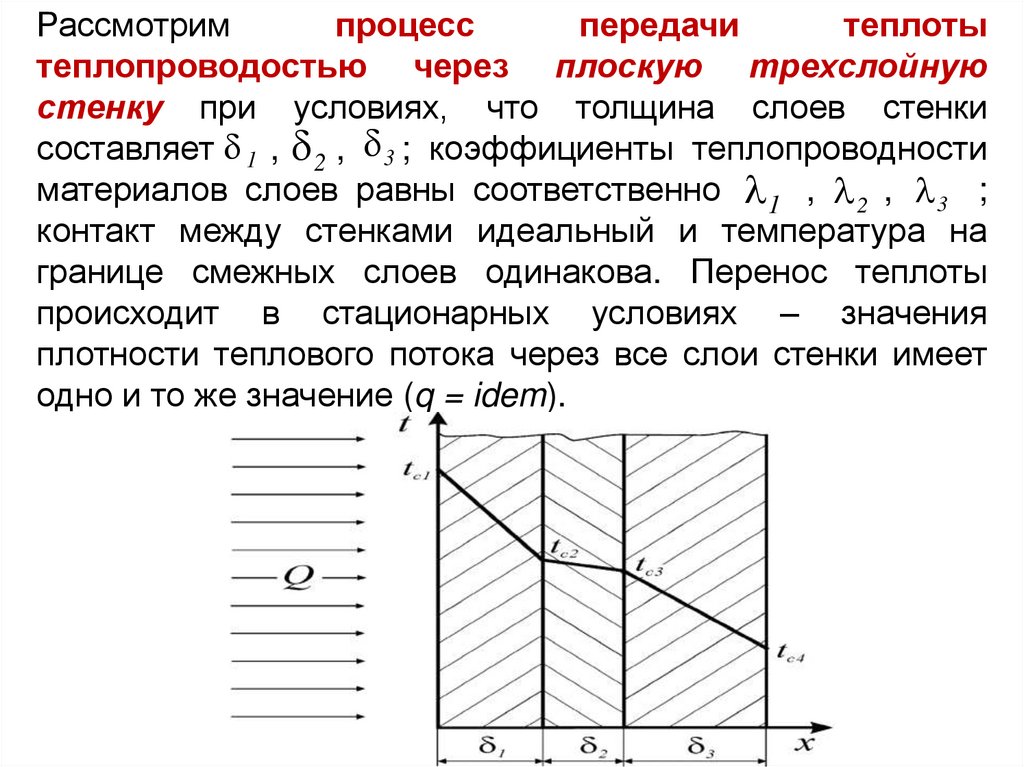
23.

Рассмотрим
процесс
передачи
теплоты
теплопроводостью через плоскую трехслойную
стенку при условиях, что толщина слоев стенки
составляет 1 , 2 , 3 ; коэффициенты теплопроводности
материалов слоев равны соответственно 1 , 2 , 3 ;
контакт между стенками идеальный и температура на
границе смежных слоев одинакова. Перенос теплоты
происходит в стационарных условиях – значения
плотности теплового потока через все слои стенки имеет
одно и то же значение (q = idem).

24.

Запишем уравнение теплопроводности для каждого из
слоев многослойной плоской стенки, выделим из эти
уравнений разности температур tс1 tс 2 q 1 q R1 ;
1
tс 2 tс 3 q 2 q R2 ;
2
tс 3 tс 4 q 3 q R3 .
3
просуммируем эти уравнения
1 2 3
q R1 R2 R3 .
tс1 tс 4 q
1 2 3
получим уравнение теплопроводности через трехслойную
t с1 t с 4
t с1 t с 4
плоскую стенку
q
.
1 2 3 R1 R2 R3
1 2 3
t с1 t с n 1 t с1 t с n 1 tс1 t с n 1
Если в стенке n слоев,
q
,
n
n
i
R
уравнение примет вид:
R
i
i 1
i 1 i

25. Теплопроводность цилиндрической стенки

Рассмотрим процесс передачи теплоты теплопроводностью
через цилиндрическую однослойную стенку с внутренним
d1=2r1 и наружным диаметром d2=2r2 в условиях
t
0
стационарного температурного поля
.
Внутренние источники
теплоты отсутствуют (qv=0).
Дифференциальное уравнение теплопроводности
через цилиндрическую стенку в рассматриваемых
условиях имеет следующий вид:
2t 1 t 1 2t 2t
t
a 2
2 2 2 0
r r r z
r

26.

Температуры на наружной и внутренней поверхности
цилиндрической стенки неизменны и по оси z, совпадающей с
осью цилиндра, температура также не изменяется:
2t
2t
0
0
2
2
z
При данных условиях температура изменяется только по
радиусу и дифференциальное уравнение теплопроводности
принимает следующий вид:
d 2 t 1 dt
0
2
d r r dr
Граничные условия:
t t с1 ,
при r r1
при r r2
t tс 2
dt
Если u
, то дифф. ур. можно представить в виде
du u
dr
0
dr r

27.

Интегрируя соотношение, получим
ln u ln r ln C1
Потенцируя это выражение и переходя к первоначальным
переменным, имеем
dr
dt C1
r
t C1 ln r C2
После интегрирования, получим
Постоянные интегрирования С1 и С2 определяются из
граничных условий:
t c1 C1 ln r1 C 2
tc 2 C1 ln r2 C2
t c1 t c 2
ln r1
С1
С2 t c1 t c1 t c 2
r1
r1
ln
ln
r2
r2
Уравнения температурного поля цилиндрической стенки r
собой уравнение логарифмической кривой
ln
Отсюда
t t c1 t c1 t c 2
r1
r2
ln
r1

28.

Для определения теплового потока через цилиндрическую
стенку воспользуемся законом Фурье
t
Q F
r
F 2 r l
Учитывая то, что
, после интегрирования
получаем
выражение
для
теплового
потока
через
цилиндрическую стенку
2 l t t
Q
или
2 l tc1 tc 2 l tс1 tс 2
Q
d2
d2
1
ln
ln
d1
2
d1
c1
c2
r2
ln
r1
Тепловой поток через единицу длины цилиндрической стенки –
линейная плотность теплового потока (ql, Вm/м)
Q tc1 tc 2
ql
d2
1
l
ln
2
d1

29.

Линейная плотность теплового потока для многослойной
цилиндрической стенки
i n
t c1 t c n 1
ql i n
d i 1
1
2 ln d
i 1
i
i
d i 1
1
2 ln d
где
- линейное термическое сопротивление
i 1
i
i
многослойной цилиндрической стенки.
Температура на границе любых двух слоев многослойной
цилиндрической стенки
ql j 1
d i 1
tc( j 1 ) tc1
ln
i 1 2 i
di

30. Теплопроводность криволинейной стенки

Q Fm tc1 tc 2 .
где расчетная площадь поверхности теплопроводности Fm
определяется в зависимости от формы стенки, через которую
происходит передача теплоты:
F1 F2
Fm Fma
;
для плоской стенки
2
для цилиндрической стенки
Fm FmL F2 F1 ln F2 F1 ;
Fm FmG F1 F2 .
для сферической стенки
Тепловой поток через многослойные криволинейные стенки
t с 1 t с n 1
Q n
i
F
i 1 i
mi
Представленные уравнения называются
уравнениями стационарной теплопроводности.
обобщенными

31.

Спасибо за внимание !
СПАСИБО ЗА ВНИМАНИЕ !