Методы математической обработки данных

1.

2. Основные понятия математической статистики

3. Предмет математическая статистика

Математическая статистика -
раздел математики, изучающий
методы сбора, описания и анализа
данных наблюдений и эксперимента с
целью выявления статистических
закономерностей и построения
вероятностных моделей массовых
случайных величин.

4. Предмет математическая статистика

Основная задача математической
статистики - получение достоверных
выводов, достоверной информации о
распределении случайной величины,
полученной непосредственно в
результате наблюдений, на основе
экспериментальных данных.

5. Предмет математическая статистика

Математическая
статистика
Теория
вероятности

6. Предмет математическая статистика

Основная цель статистического
исследования — обнаружение и
анализ зависимостей между
статистическими данными и их
использованием для прогнозирования
и принятия решений о распределении
признака (случайной величины) у
изучаемых объектов.

7. Предмет математическая статистика

Математическая статистика позволяет
указать способы сбора, группировки значений
признака, которые получены у испытуемых в ходе
психологического, педагогического исследования,
наблюдений;
для обработки полученных результатов определить
методы анализа статистических данных в зависимости
от цели исследования (произвести оценку вероятности
события, оценку функции распределения, оценку
зависимости случайной величины от других случайных
величин и т.д.);
осуществить проверку статистических гипотез
(осуществить согласование результатов оценивания с
опытными наблюдаемыми данными).

8. История развития математической статистики

Математическая статистика возникла в XVII
веке и развивалась одновременно с
теорией вероятности. Во второй половине
XIX — начале XX века на формирование
математической статистики повлияли
труды и исследования П.Л. Чебышева, А.А.
Маркова, A.M. Ляпунова, К. Гаусса, А.
Кетле, Ф. Гальтона, К. Пирсона.
Дальнейшее развитие математической
статистики связано с работами К. Крамера,
Р. Фишера, Ю. Негомана и др.

9. Основные понятия

Случайная величина (в теории
вероятности) — это такая величина,
которая может принимать различные
числовые значения из множества всех
возможных

10. Случайные величины

Дискретная величина –
случайная величина,
которая принимает
лишь множество
«изолированных друг
от друга» значений,
например, только
целочисленные
значения.
Пример: число
допущенных детьми
ошибок при
выполнении заданий.
Непрерывной
называется случайная
величина,
всевозможные
значения которой
заполняют весь
конечный или
бесконечный
промежуток числовой
оси.
Пример: температура,
измеряемая в течение
некоторого интервала
времени.

11. Основные понятия

Измерение — это установление
взаимно однозначного соответствия
между объектами или явлениями и
числами в соответствии с
определенными правилами.

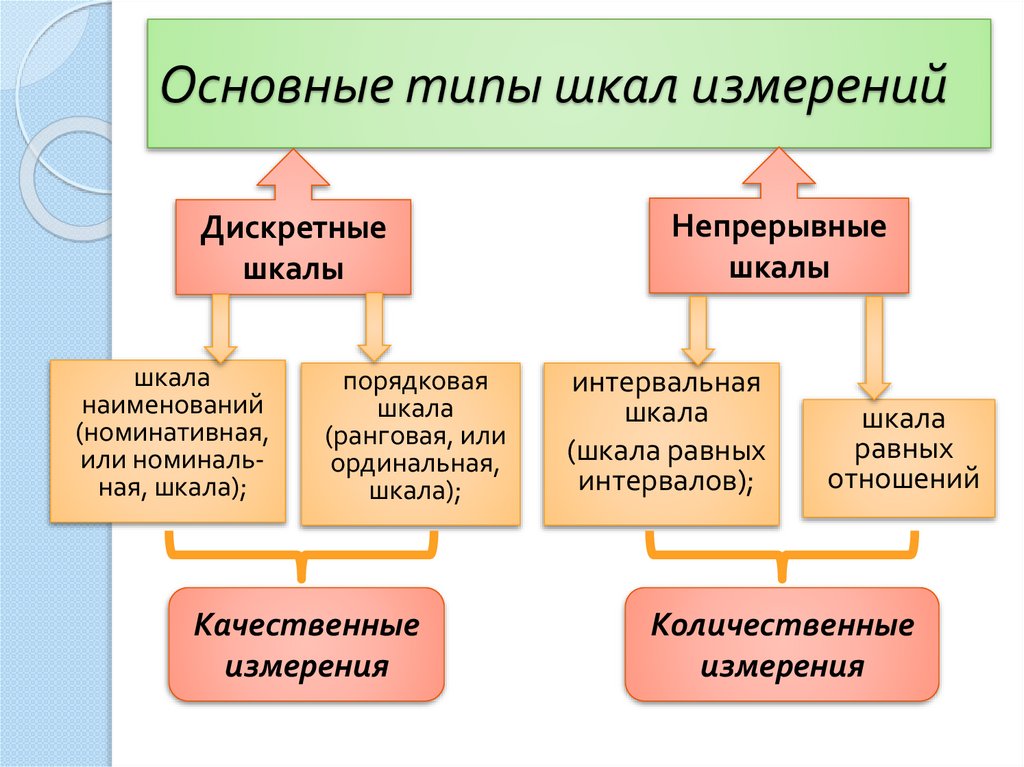
12. Основные типы шкал измерений

Дискретные
шкалы
шкала
наименований
(номинативная,
или номинальная, шкала);
порядковая
шкала
(ранговая, или
ординальная,
шкала);
Качественные
измерения
Непрерывные
шкалы
интервальная
шкала
(шкала равных
интервалов);
шкала
равных
отношений
Количественные
измерения

13. Основные типы шкал измерений. Шкала наименований.

При измерении рассматриваемого свойства
объектов или явления позволяет в соответствии
с установленным критерием разделить эти
объекты на несколько классов (групп) по
состоянию измеряемого свойства.

14. Основные типы шкал измерений. Порядковая шкала.

При измерении рассматриваемого свойства объектов или
явления позволяет в соответствии с установленным
критерием задать на множестве объектов или явлений
отношение равенства и порядка по состоянию
исследуемого свойства. В порядковой шкале классы
(группы) образуют последовательность от самого
«низкого» к самому «высокому» классу или наоборот.

15. Основные типы шкал измерений. Интервальная шкала.

При измерении рассматриваемого свойства объектов или
явления возможно, если при помощи установленного
критерия получится измерить интервал между состоянием
исследуемого свойства, признака у объектов, то есть
установить, на сколько единиц измеряемый признак у
одного объекта меньше или больше, чем у другого.

16. Основные типы шкал измерений. Шкала равных отношений.

позволяет распределить объекты, субъекты пропорционально степени выраженности у них измеряемого свойства,
признака, то есть установить не только, на сколько единиц
измеряемый признак проявляется у одного объекта
меньше или больше, чем у другого, но и во сколько раз
меньше или больше. Это свойство шкалы предполагает
наличие начала отчета, нулевой точки (абсолютного нуля).

17. Нормальный закон распределения случайной величины.

В педагогических, психологических
исследованиях чаше всего для обработки
результатов используют методы, основанные на
нормальном законе распределения случайной
величины.

18. Основные понятия

Генеральная совокупность — это всевозможные
наблюдения изучаемого показателя, свойства,
признака, все исходы случайного испытания,
вся совокупность распределения случайной
величины у всех объектов, обладающих
признаком, свойством, который интересует
исследователя.
Выборочная совокупность (выборка) —
это совокупность объектов, выбранных
из генеральной совокупности случайным образом.

19. Основные понятия

Репрезентативная выборка – выборка ,
в которой присутствуют все значения
случайной величины в тех же
пропорциях, что и в генеральной
совокупности.
Объем выборки - число объектов
(наблюдений) в совокупности.
Обозначения:
N - объем генеральной совокупности;
п - объем выборки.

20. Основные понятия

Вариационный ряд - упорядоченный в
порядке возрастания (убывания) ряд
полученных в ходе исследования
значений измеряемого признака,
свойства объекта.
Распределением случайной величины
Х называется всякое соответствие
между возможными значениями
случайной величины X и вероятностями
их появления.

21. Основные понятия

Медиана случайной величины X - это средний
элемент выборки, в которой все элементы
упорядочены по возрастанию (убыванию), если
в упорядоченной выборке четное число
элементов, то находится среднее
арифметическое двух средних элементов.
Мода случайной величины X — это
то(те) ее значение(я), которое(ые)
имеет(ют) наибольшую вероятность
появления).

22. Основные понятия.

Параметры распределения - числовые
характеристики, которые показывают
расположение значений измеряемого
признака, свойства, изменчивость этих
значений, наибольшую вероятность
появления определенных значений
измеряемого признака, свойства объектов.
В математической статистике наиболее
важными параметрами распределения
являются математическое ожидание,
дисперсия,
показатели асимметрии,
Показатели эксцесса.

23. Математическое ожидание случайной величины

Математическое ожидание случайной
величины — это среднее значение
случайной величины X при стремлении
количества измерений исследуемого
признака, свойства к бесконечности.
Если X — дискретная случайная величина,
то ее математическим ожиданием M[X],
или выборочным средним