Similar presentations:
Задачи и методы математической статистики. Выборочный метод
1. Задачи и методы математической статистики. Выборочный метод
Кафедра медицинской и биологической физикиЗадачи и методы
математической
статистики. Выборочный
метод
Лекция №1
для студентов 2 курса,
обучающихся по специальности 060609 –
Медицинская кибернетика
доц. Шапиро Л.А.
Красноярск, 2015 г.
2. План лекции:
1. Задачи и методы математическойстатистики.
2. Основные понятия выборочного метода.
3. Статистическое распределение выборки.
Эмпирическая функция распределения,
гистограмма.
4. Статистические оценки параметров
распределения.
5. Свойства выборочных характеристик.
3. Актуальность темы
Основные понятия и методыматематической статистики
необходимы для обработки
результатов измерений в медицине
и биологии
4.
Теория вероятностей занимаетсяпостроением и изучением вероятностных
моделей случайных явлений. Эти модели
строятся на основе аналитических
исследований изучаемых случайных
явлений. По вероятностным моделям мы
можем рассчитать вероятность любого
события изучаемого случайного явления.
5.
Предмет математическойстатистики составляет разработка
методов регистрации, описания и
анализа статистических
экспериментальных данных,
получаемых в результате
наблюдения массовых случайных
явлений
6. Задачи математической статистики:
По результатам случайныхэкспериментов (выборкам) сделать
содержательные выводы о
вероятностных моделях, адекватно
отражающих закономерности
изменения замеряемых признаков в
изучаемых процессах, явлениях
7.
Статистикаслучайных
величин
(одномерная
статистика )
Многомерная
статистика
(факторный
анализ)
Временные
ряды
8. Задачи одномерной статистики
Описательная статистика(представление
экспериментальных данных,
определение точечных и
интервальных оценок)
Проверка статистических гипотез
(о законе распределения,
параметрах распределения)
9. Основные понятия выборочного метода
Наиболее общую совокупность,подлежащих изучению объектов называют
генеральной
Выборочной совокупностью или просто
выборкой называют часть генеральной
совокупности, случайным образом
отобранной для наблюдений
Обьемом совокупности называется число
объектов этой совокупности (генеральной
или выборочной)
10. Выборочные совокупности
n<30 -малые30<n<100 - средние
n>100 –большие
Цель: С помощью статистических методов
по свойствам выборки сделать вывод о
свойствах генеральной совокупности.
Выборка
должна
быть
репрезентативна
(представительна), то есть организована таким
образом, чтобы отражать, по-возможности, все
интересующие
нас
свойства
генеральной
совокупности.
Выборка считается репрезентативной, если
каждый объект выборки отобран случайно из
генеральной совокупности, то есть все объекты
имеют одинаковую вероятность попасть в выборку.
11.
ПовторныеБесповторные
Объекты
возвращаются в
генеральную
совокупность
Объекты не
возвращаются в
генеральную
совокупность
12.
Отбор, нетребующий
разделения
генеральной
совокупности на
части:
1. Простой случайный
бесповторный отбор
2. Простой
случайный
повторный отбор
Отбор, при котором
генеральная
совокупность
разбивается на
части:
1. Типический отбор
2. Механический отбор
3. Серийный отбор
13.
Типический отбор– объекты
отбираются не из всей генеральной
совокупности, а из каждой ее
«типической» части
Механический отбор
– генеральная
совокупность делится на столько групп,
сколько объектов должно войти в
выборки и из каждой группы
отбирается по одному объекту
Серийный отбор
- объекты отбираются
из генеральной совокупности не по
одному, а сериями
На практике часто используются комбинированные методы
14.
количественныекачественные
порядковые
(полуколичественные)
номинальные
бинарные
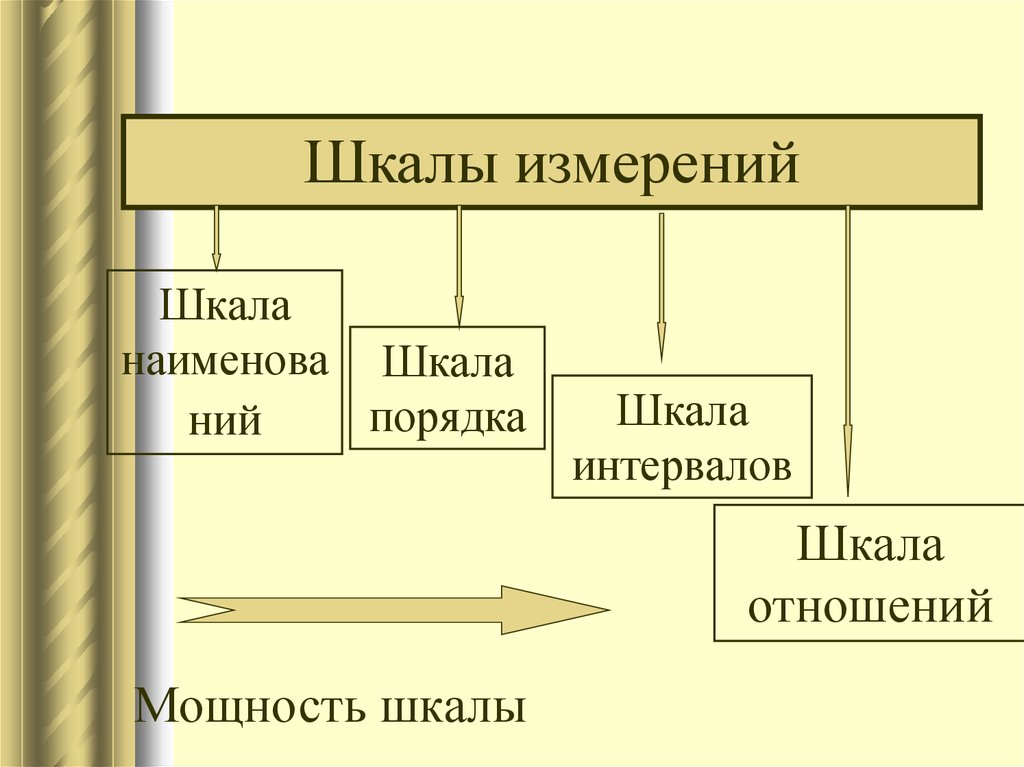
15. Шкалы измерений
Шкаланаименова Шкала
порядка
ний
Шкала
интервалов
Шкала
отношений
Мощность шкалы
16. Шкалы и допустимые преобразования
ШкалаДопустимое
преобразование
Наименований
Взаимно-однозначное
Порядковая
Строго возрастающее
Интервальная
Линейное
Отношений
Подобия
17.
Значения изучаемого признаканазываются вариантами
Последовательность вариант,
расположенных в возрастающем
порядке называется
вариационным рядом
Например: 172, 179, 158, 186, 164
Вариационный ряд:
158, 164, 172, 179, 186
18.
дискретныенепрерывные
Статистическим рядом распределения
называется набор вариант и
соответствующих им абсолютных и
относительных частот
19. Статистический ряд распределения
ХX1
X2
…
m
m1
m2
…
mn
m/n
m1/n
m2/n
…
mn
Xn
20. Дискретный ряд распределения (индекс КПУ)
2 3 4 4 2 5 4 2 3 3 3 3 5 5 4 43 3 4 4 4 4 4 3 3 4 4 4 4 4
n=30
КПУ
2
3
4
5
m
3
9
15
3
m/n
3/30=
0,1
9/30=
0,3
15/30=
0,5
3/30=
0,1
n
P( x i ) 1
i 1
условие нормировки
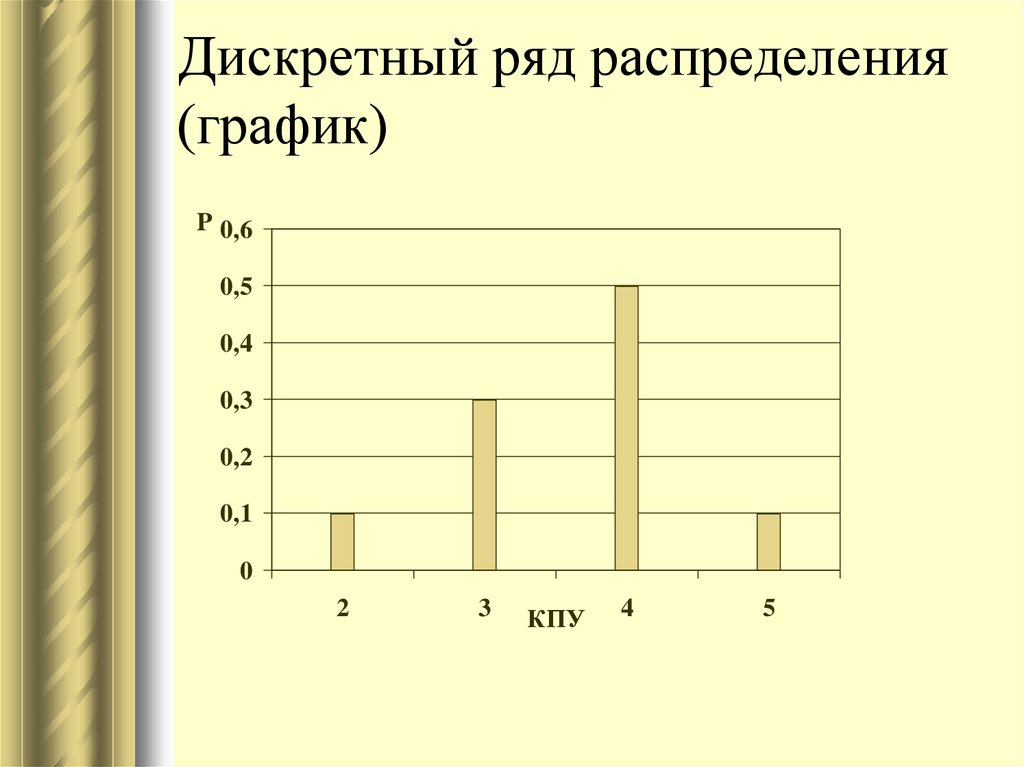
21. Дискретный ряд распределения (график)
P 0,60,5
0,4
0,3
0,2
0,1
0
2
3
КПУ
4
5
22. Статистическая функция распределения
Пусть х1,…,хn - выборка наблюденийслучайной величины X с функцией
распределения F(x). Необходимо по выборке
оценить функцию распределения.
Определение. Статистической (иногда –
эмпирической) функцией распределения
случайной величины X называется частота
события X x в данном статистическом
материале:
F*(x) = m/n,
где m – число Xi, таких, что Xi x.
23.
Эмпирическая функция распределенияимеет скачки в точках выборки
(вариационного ряда), величина скачка в
точке xi равна m/n, где m–количество
элементов выборки, совпадающих с xi.
Эмпирическая функция распределения
по вариационному ряду строится так:
0 если x x1
k
*
Fn ( x ) если xk x x( k 1)
1n при x x
n
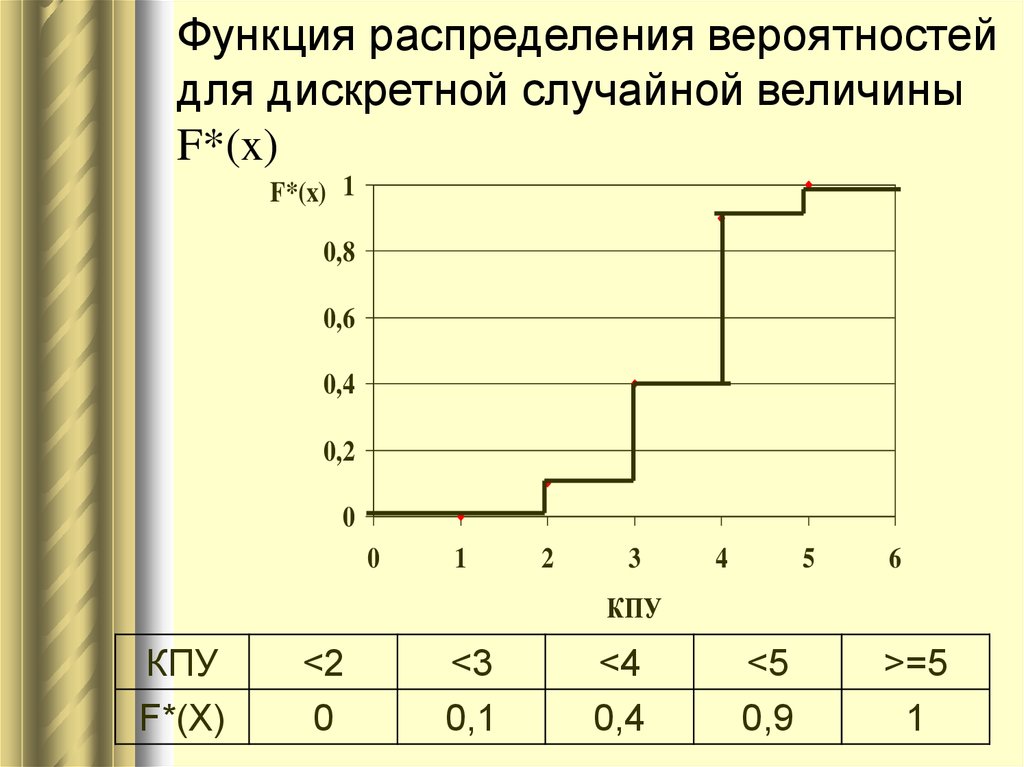
24. Функция распределения вероятностей для дискретной случайной величины F*(x)
F*(x) 10,8
0,6
0,4
0,2
0
0
1
2
3
4
5
6
КПУ
КПУ
F*(X)
<2
0
<3
0,1
<4
0,4
<5
0,9
>=5
1
25. Эмпирическая функция распределения
0 если x 20
,
1
если
2
x
3
*
Fn ( x ) 0,4 если 3 x 4
0,9 если 4 x 5
1 при x 5
26. Интервальные ряды распределения
Ряд распределения студентов по росту148
151
172
154
185
162
158
169
158
161
172
164
164
169
155
149
152
177
167
161
154
165
162
171
166
173
153
167
179
170
165
157
176
168
163
165
156
174
149
145
162
166
160
189
157
159
163
184
172
159
27. На практике ряд распределения (вариационный ряд) составляют следующим образом:
Из имеющихся значений признака x выбираютнаименьшее (Xmin), наибольшее (Xmax),
определяют размах распределения
(Xmax – Xmin).
189-145=44
Определяют число классов группировки. Для
определения числа классов можно
воспользоваться формулой: k=1+3,32·lg n, где
n – число измерений. Величину k округляют до
целых чисел (формула Стерджесса).
Например, при n=50:
k=1+3,32·lg 50=1+3,32·1,7=6,64 7
k 3 n 3 50 4,6
28. Интервальные ряды распределения
Определяют оптимальную величину класса (интервалагруппировки)
x max x min
xi
k
Эту величину также можно округлять соответственно точности
значений x.
Xi=44/4,6 =9,5 10
Выбирают границы классов. Границы первого класса следует
выбрать так, чтобы он содержал наименьшее значение, но не
начинался с него, например, класс может начинаться с
величины (Xmin – x i ).
2
Последующие классы
образуются добавлением величины
интервала Xi. Если нижняя граница класса совпадает с
верхней границей предыдущего класса, это значение следует
отнести к данному классу. Например, [1–2), [2–3) и т.д.
29.
Статистический ряд распределениястудентов по росту
X
m
m/n
140150
4
150160
14
160170
20
170180
9
180190
3
4/50 14/50 20/50 9/50 3/50
0,08
0,28
0,4
0,18 0,06
f ( x ) 0,08/10
m
0,008 0,028 0,04 0,018 0,006
n x
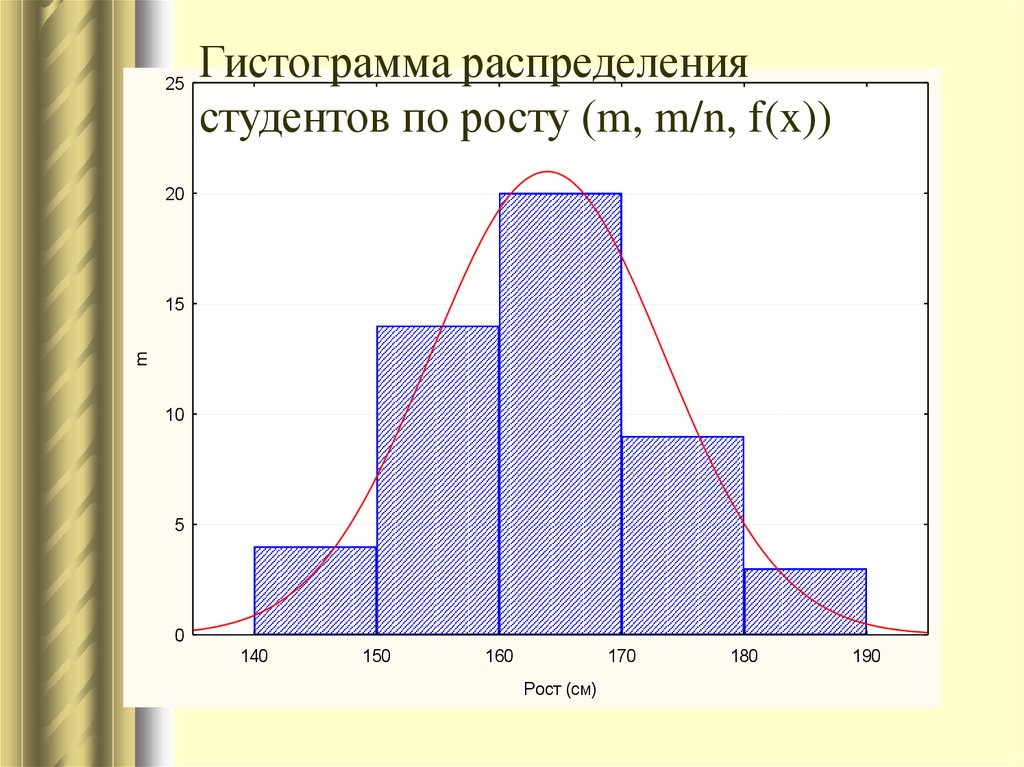
30.
25Гистограмма распределения
студентов по росту (m, m/n, f(x))
20
m
15
10
5
0
140
150
160
170
Рост (см)
180
190
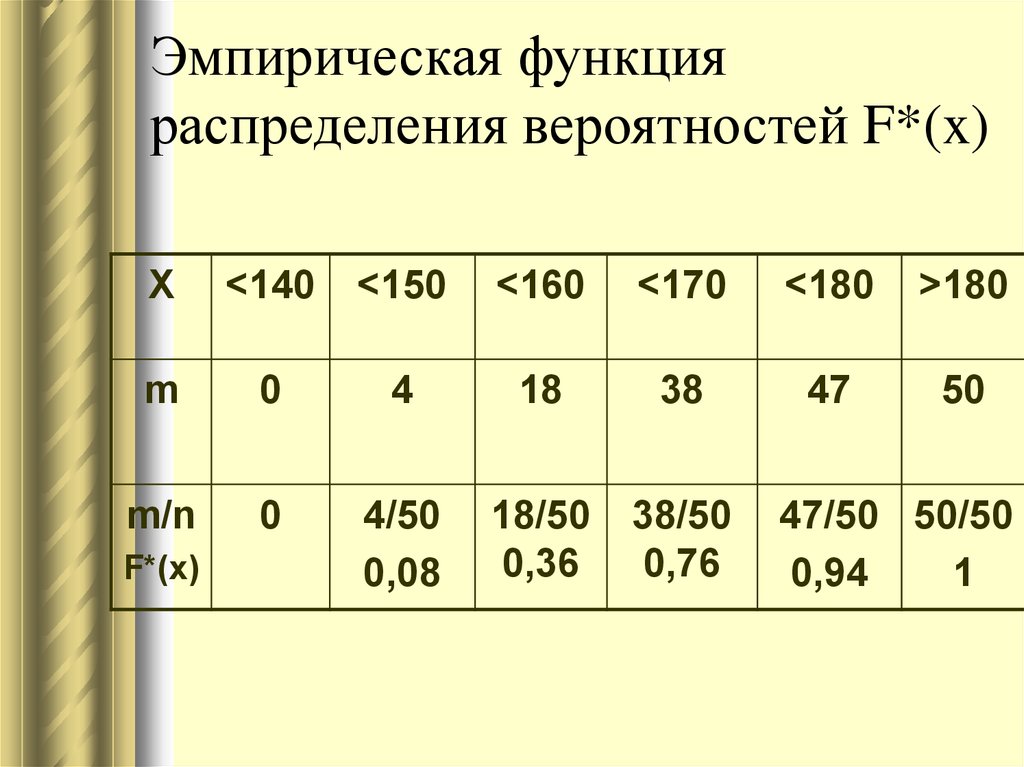
31. Эмпирическая функция распределения вероятностей F*(x)
X<140
<150
<160
<170
<180
>180
m
0
4
18
38
47
50
m/n
0
4/50
0,08
18/50
0,36
38/50
0,76
F*(x)
47/50 50/50
0,94
1
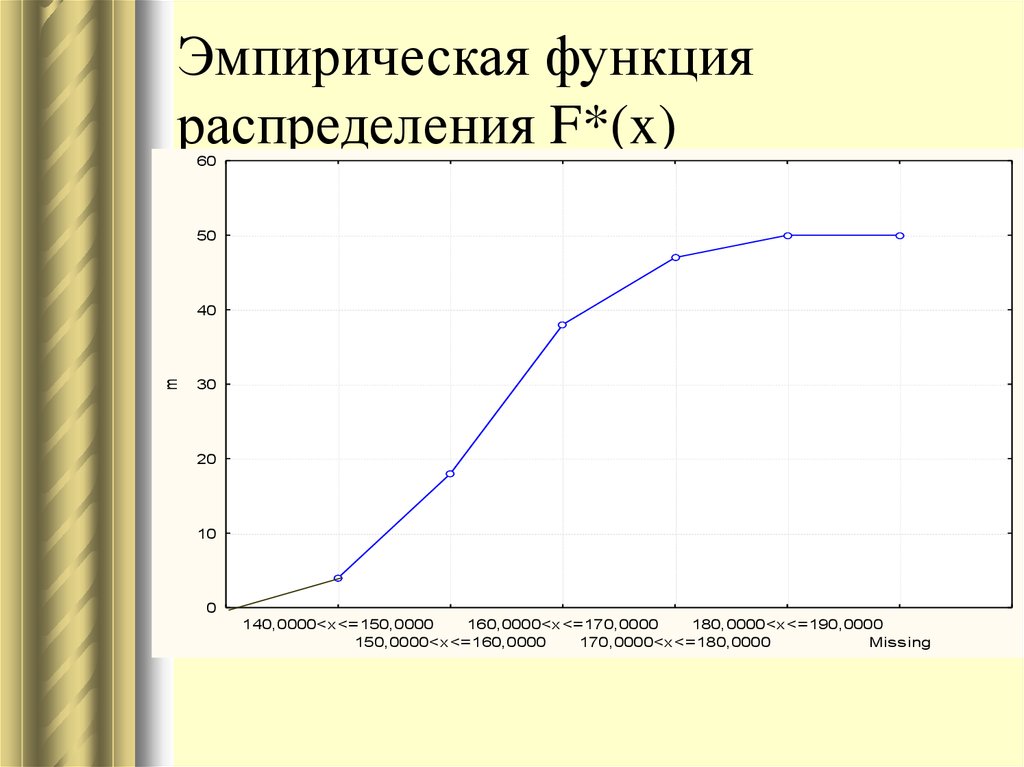
32. Эмпирическая функция распределения F*(x)
6050
m
40
30
20
10
0
140,0000<x<=150,0000
160,0000<x<=170,0000
180,0000<x<=190,0000
150,0000<x<=160,0000
170,0000<x<=180,0000
Missing
33. Статистические оценки параметров распределения
Задача: Изучить количественный признакгенеральной совокупности.
Если можно теоретически оценить вид
распределения, то необходимо
вычислить соответствующие параметры:
Нормальное
распределение
M(x) и
Распределение
Пуассона
параметр λ
Биномиальное
распределение
p
и т.д.
34.
Пусть для изучения признака вгенеральной совокупности
извлечена выборка объемом n:
x1, x2, x3, …, xn
Статистической оценкой
(статистикой) неизвестного
параметра теоретического
распределения называют функцию
от наблюдаемых случайных
величин Θn(х1,…,хn)
35.
Истинныемоменты
М(Х)=а
D(X)= 2
k
Начальные
моменты
μk
Центральные
моменты
Оценки для истинных
моментов
n
x
m x
i i
i 1
D( x ) s 2
nn
2
m
(
x
x
)
i
i 1
n
n
1
k
k
x xi mi
n i 1
1 n
k ( xi x )k mi
n i 1
36.
В качестве оценки М(X) используетсявыборочное среднее:
1. Если значения признака x1, x2, x3, …, xn имеют
соответственно частоты m1, m2, m3, …, mn ,
причем m1+m2+m3+ …+ mn=n
n
x1m1 x2m2 ... xn mn
x
n
m x
i i
i 1
n
2. Если все значения признака различны, mi =1:
n
x
x1 x2 ... xn
x
n
n
i 1
i
Средняя арифметическая есть средняя взвешенная
значений признака с весами, равными
соответствующим частотам
37.
Отклонением называют разность междузначением признака и его средней
арифметической
(x x)
Сумма произведений отклонений на
соответствующие частоты равна 0:
m ( x x ) 0
i
Среднее значение отклонений равно 0:
m (x x) m (x x) 0 0
n
n
m
i
i
i
38.
• Оценкой D(X) служит выборочнаядисперсия:
n
• 1.
D( x ) s 2
2
m
(
x
x
)
i i
i 1
n
• 2.
n
D( x ) s 2
2
(
x
x
)
i
i 1
n
• Среднее квадратическое отклонение:
s
D(х)
39.
Асимметрия-скошенностьраспределения
Эксцесс-островершинность
распределения
Обычно рассматривают безразмерные
коэффициенты асимметрии и эксцесса:
3
Sk 3
4
Ex 4 3
3
(x x) m
Sk А
i
i
n s
4
( xi x ) mi
3
E
n s
4
3
40. Коэффициент вариации
Характеризует относительноезначение среднего квадратического
отклонения и служит для сравнения
разброса несоизмеримых показателей
s
V 100%
x
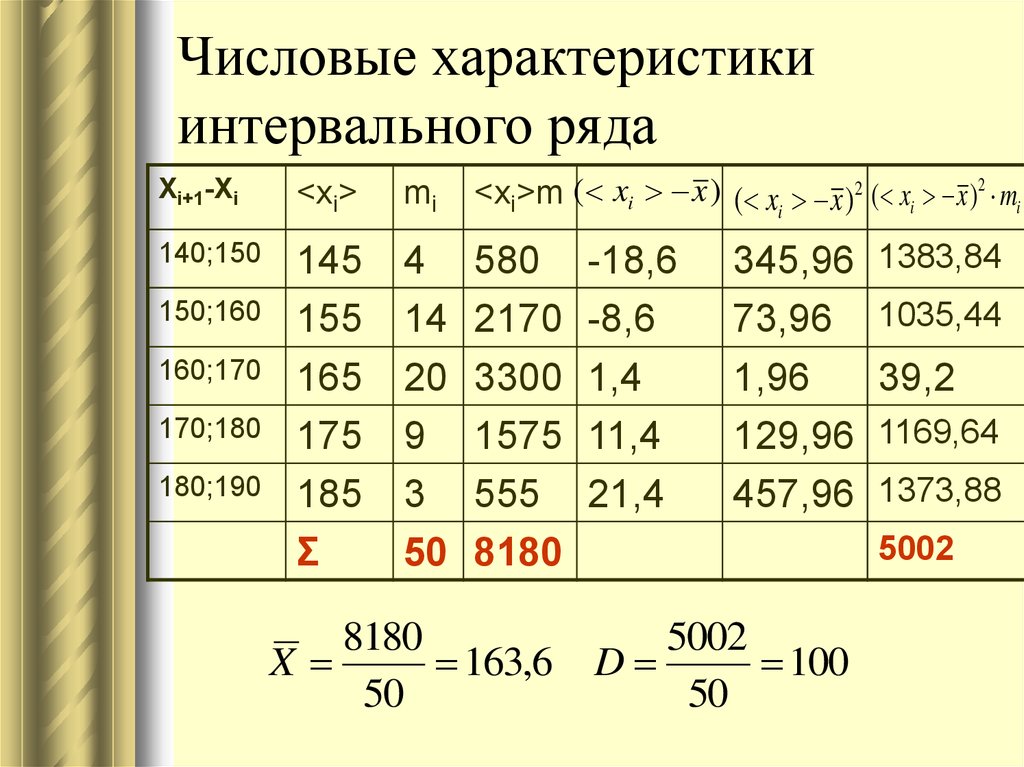
41. Числовые характеристики интервального ряда
Xi+1-Xi<xi>
mi
<xi>m ( xi x ) ( xi x )2 ( xi x )2 mi
140;150
145
155
165
175
185
Σ
4
14
20
9
3
50
580
2170
3300
1575
555
8180
150;160
160;170
170;180
180;190
8180
X
163,6
50
-18,6
-8,6
1,4
11,4
21,4
345,96
73,96
1,96
129,96
457,96
1383,84
1035,44
39,2
1169,64
1373,88
5002
5002
D
100
50
42. поправка Шеппарда При вычислении выборочной дисперсии для уменьшения ошибки, вызванной группировкой (особенно при малом числе интервалов
поправка ШеппардаПри вычислении выборочной дисперсии для
уменьшения ошибки, вызванной группировкой
(особенно при малом числе интервалов)
вычитают из вычисленной дисперсии 1/12
квадрата длины частичного интервала:
D'в =Dв-(1/12)h2
D=100 - (1/12) 100=91,67
s 91,67 9,6
9,6
V
100% 5,9%
163,6
43. Коэффициенты асимметрии и эксцесса:
mi4
14
20
9
3
Σ=50
( xi x )3( xi x )3 mi ( xi x ) 4 ( xi x )4 mi
-6434,86 -25739,4 119688,3
-636,06
2,744
1481,5
9800,3
-8904,78
13333,9
29401,03
555
8145,6
8145,6
A
0,184
3
50 9,6
5470,08
3,84
16889,6
209727,4
478753,3
76581,14
76,832
152006,4
629182,1
1336600
1336600
E
3 0,147
4
50 9,6
44. Заключение
Нами рассмотрены:Основные понятия выборочного
метода;
Способы построения дискретных и
интервальных вариационных рядов.
45. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:
Основная литература:Попов А.М. Теория вероятней и
математическая статистика /А.М. Попов, В.Н.
Сотников. – М.: ЮРАЙТ, 2011. – 440 с.
Герасимов А. Н. Медицинская статистика:
учебное пособие / А. Н. Герасимов. – М. : Мед.
информ. агентство, 2007. – 480 с.
Балдин К. В. Основы теории вероятностей и
математической статистики : учебник / К. В.
Балдин. – М. : Флинта, 2010. – 488с.
Учебно–методические пособия:
Шапиро Л.А., Шилина Н.Г. Руководство к
практическим занятиям по медицинской и
биологической статистике Красноярск: ООО
«Поликом». – 2003.





































 mathematics
mathematics








