Similar presentations:
Описательная статистика. Выборочный метод
1. Описательная статистика
Выборочный методЗадачи математической статистики:
1) Сбор
данных 2) Анализ 3) Интерпретация 4) Прогноз
генеральная
случайная
МС
ТВ
величина
совокупность
X
х1 , х2 ,...,хn выборка из генеральной совокупности
Идея выборочного метода: по выборке получить
представление о генеральной совокупности
Репрезентативность выборки
Способы отбора: 1) случайный повторный
2) случайный бесповторный
1
2. Описательная статистика
Способы представления выборочных данных:1)
2)
3)
4)
первоначальные статистические данные
вариационный ряд
статистический ряд
сгруппированный статистический ряд
х1 , х2 ,...,хn- числовые значения в порядке отбора
х 1 , х 2 ,...,х n - упорядочены по возрастанию
~
xj
nj
[~
x j ;~
xj)
nj
различные варианты
количество наблюдений каждой
интервалы значений вариант
кол-во наблюдений в каждом
2
3.
Оценка закона распределенияпо выборочным данным
1) полигон - оценка многоугольника распределения
2) гистограмма – оценка плотности распределения
3) эмпирическая функция распределения
3
4. Распределения статистик
X~
Статистические копии
- генеральная совокупность
- параметр генеральной совокупности
;
- оценка параметра по выборке
х1 , х2 ,...,хn
X 1 , X 2 ,...,X n
- числовые значения
- случайные величины
Статистические 1) независимые
копии:
2) одинаково распределенные
К X 1 , X 2 ,...,X n
- статистика
(выборочная функция)
4
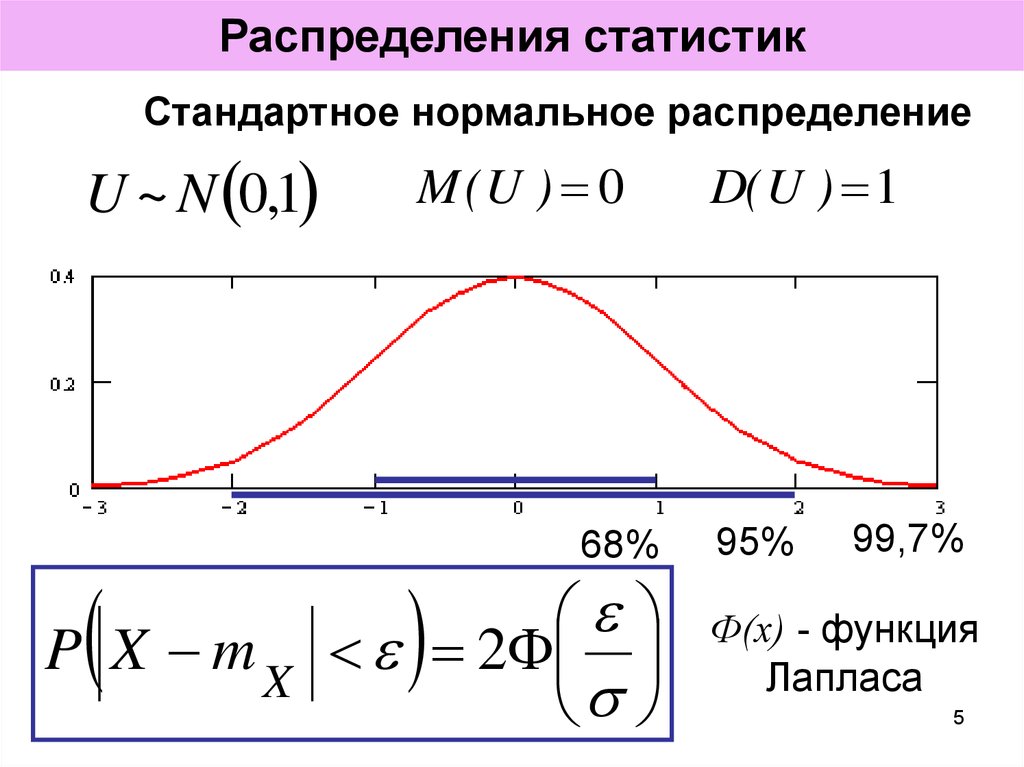
5. Распределения статистик
Стандартное нормальное распределениеU ~ N 0,1
P X mX
M (U ) 0
68%
2
D( U ) 1
95%
99,7%
Ф(х) - функция
Лапласа
5
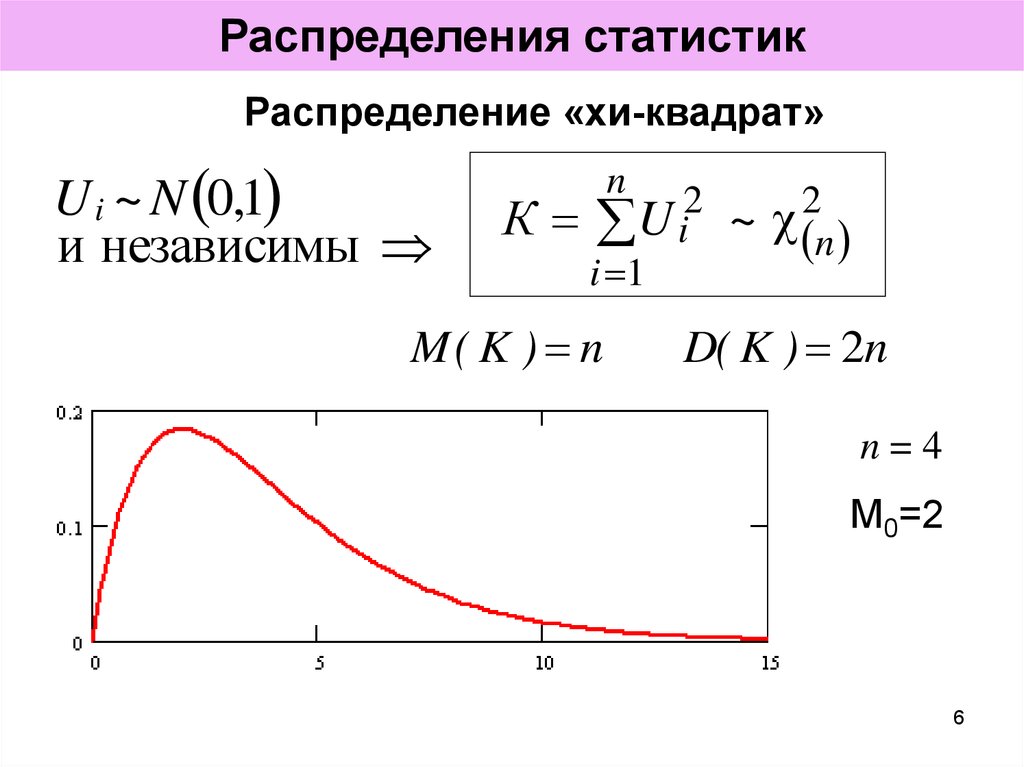
6. Распределения статистик
Распределение «хи-квадрат»U i ~ N 0,1
и независимы
К
n
2
U i
i 1
M( K ) n
~
2
n
D( K ) 2n
n=4
M0=2
6
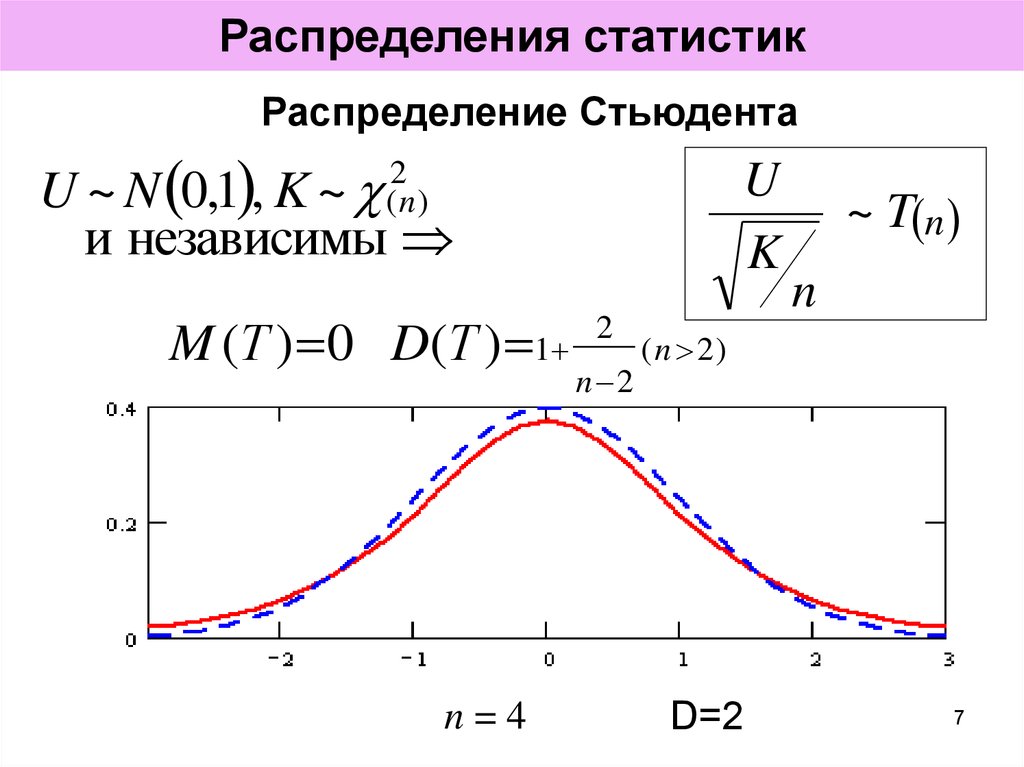
7. Распределения статистик
Распределение СтьюдентаU ~ N 0,1 , K ~
и независимы
2
(n )
M (Т ) 0 D(Т ) 1
n=4
U
K
2
n 2
~ T n
n
( n 2)
D=2
7
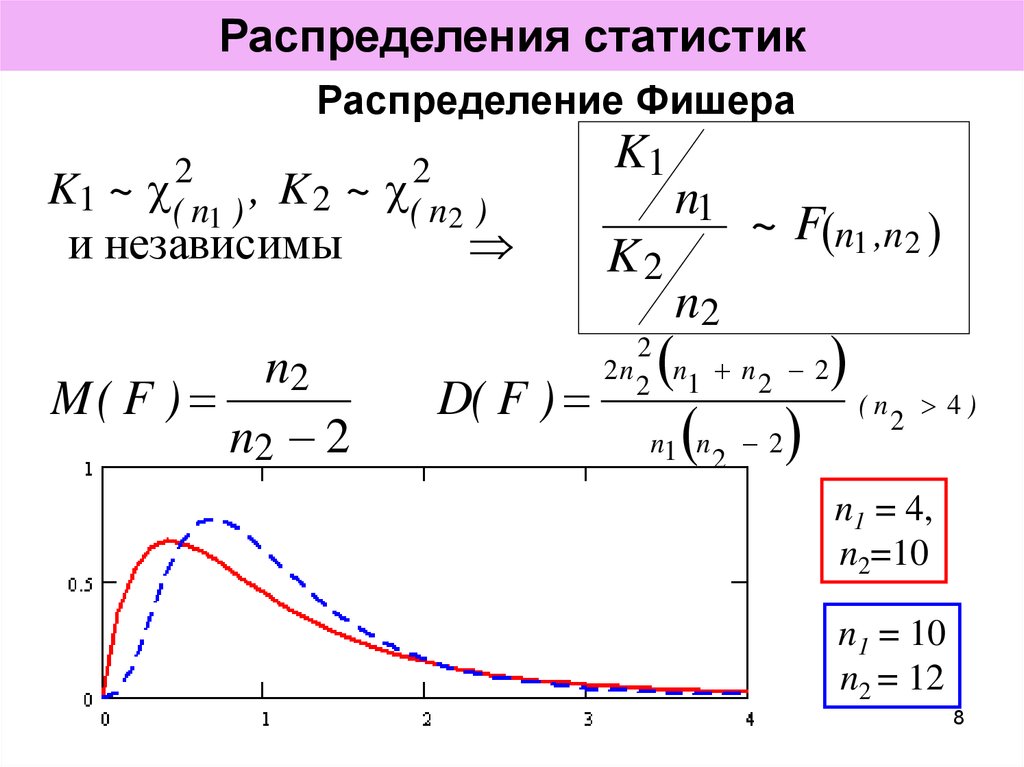
8. Распределения статистик
Распределение Фишера(2n ) ,
1
K1 ~
K2 ~
и независимы
n2
M( F )
n2 2
(2n )
2
D( F )
K1
K2
n1
~ F n1 ,n 2
n2
2
2 n n1 n 2 2
2
n1 n 2
2
(n
2
4)
n1 = 4,
n2=10
n1 = 10
n2 = 12
8
9. Оценки параметров
Точечные оценки и их свойства~
Оценка называется несмещенной оценкой
~
параметра ,если
M
Примеры
1) m
~
n
1
X
Xk
n k 1
n
n
1
1
~
M M
X k M X k
n
n
k 1 k 1
- параметр;
его оценка:
1
n m m
n
среднее арифметическое несмещенная оценка
математического ожидания9
10. Точечные оценки и их свойства
Примерыn
2) D
n
~ 1
2
D
Xk X
n
2
k 1
X k m m X
~ 1
D
n k 1
смещенная оценка
n
2
2
1
X k m X m
n
n k 1
1
2
S
X k X
n 1 k 1
2
~ 1
2
2
M D
M X k m M X m
n k 1
несмещенная оценка
D
D D X D
n
n
10
11. Точечные оценки и их свойства
Теорема 1 Эмпирические начальные моментыявляются несмещенными оценками
теоретических начальных моментов
(если последние существуют)
mr X M X
r
n
r
1
~
mr X
Xk
n k 1
n
n
r
1
1
~
M mr
M Xk
mr X mr
n k 1
n k 1
11
12. Точечные оценки и их свойства
~Оценка называется состоятельной оценкой
параметра ,если
P
X 1 ,..., X n
~
n
Примеры
состоятельных оценок
1) m
(по теореме Чебышева)
2) p
(по теореме Бернулли)
~
n
1
X
Xk
n k 1
n
* 1
~
р p
Xk
n k 1
12
13. Точечные оценки и их свойства
Несмещенная оценка ~параметра является
состоятельной,
Теорема 2
~
D 0
n
(*)
Эмпирические начальные моменты
являются состоятельными оценками
теоретических начальных моментов,
если последние существуют
По теореме 1 эти оценки несмещенные
1
~
D mr 2
n
D
n
r
Xk
k 1
1
2
n
M M
n
2r
Xk
k 1
2
1
m2 r X mr X 0
n
n
r
Xk
2
По свойству (*)
оценки
состоятельны 13
14. Точечные оценки и их свойства
Несмещенная оценка ~1 параметра называетсяболее эффективной оценкой , чем оценка ~2 ,
если ее дисперсия меньше дисперсии ~
X ~ N a , 0
Пример
~
1 X
D 1
~
a
несмещенные оценки
2
0
~n
1
2
~
D 2
~ 1.6
D 1
~ ~
2 x 0.5
D 2 1.6
~
более эффективна, чем
~
2
2
0
n
для достижения той же точности
требуется в 1.6 раз больше опытов
14
15. Точечные оценки и их свойства
~Несмещенная оценка называется
эффективной оценкой параметра , если
ее дисперсия достигает наименьшего для
данного распределения значения
Свойства оценок:
несмещенность; состоятельность;
эффективность .
Методы получения оценок:
метод моментов;
метод максимального правдоподобия.
15
16. Методы получения точечных оценок
Пусть f ( x , ) - п.р. генеральной совокупностиНайти оценку параметра ~ по выборке х1 , х2 ,...,хn
Метод моментов
Пример
~k
mk m
Оценки: несмещенность (±);
состоятельность (+);
эффективность (-)
X ~ R 0 ,b
b
m1 X
2
~
m1 x
~
b 2x
16
17. Методы получения точечных оценок
Метод максимального правдоподобиях1 , х2 ,...,хn
n
L f ( xi , )
- функция правдоподобия
i 1
argmax L
~
Пример
X ~ N a ,
1 a
2
2
Оценки: несмещенность (±);
состоятельность (+);
эффективность (±)
n
xi a 2
1 n
L
~
a x
~ 2 1
n
exp
2
2 i 1
x x
2
2
2
i
17













 mathematics
mathematics








