Методы обработки экспериментальных данных

1. Методы обработки экспериментальных данных

Кузнецов Алексей Владимирович

2. Введение

3. 1.1. Введение

Окружающий нас мир насыщен информацией…
Ее НЕОБХОДИМО обрабатывать для принятия
управленческих решений.
Существует множество мат. пакетов: MatLab, Statistica,
Statgraphics…
НО ЕСТЬ проблема…. понимание и интерпретация
результатов!
НЕОБХОДИМО ЗНАТЬ И ПОНИМАТЬ КАК И ЧТО
ПРОИСХОДИТ ВНУТРИ МАТ. ПАКЕТОВ!

4. Области применения анализа экспериментальных данных

Экономика
Менеджмент
Медицина
Социология
Геология
Контроль качества
Концепция «Шесть сигм» – система управления
компанией или ее подразделениями на основе
интенсивного использования методов анализа
разнообразных данных о деятельности компании

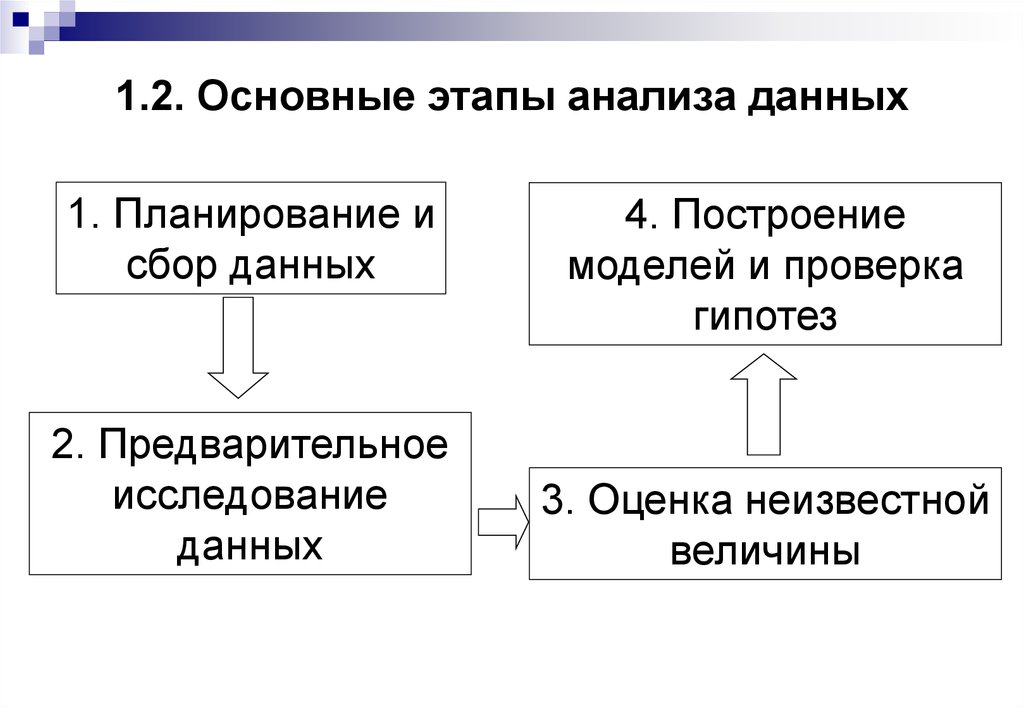
5. 1.2. Основные этапы анализа данных

1. Планирование и
сбор данных
2. Предварительное
исследование
данных
4. Построение
моделей и проверка
гипотез
3. Оценка неизвестной
величины

6. 1.3. Структуры данных

Одномерные наборы данных (одна переменная) содержат
только один признак, зарегистрированный для каждой
элементарной единицы.
Двумерные наборы данных содержат информацию о двух
признаках для каждого из объектов. В дополнение к обобщению
свойств каждой из этих двух переменных, рассматриваемых как
отдельные наборы одномерных данных,
Наборы многомерных данных содержат информацию о трех
или более признаках для каждого объекта. В дополнение к
обобщению
свойств
каждой
из
этих
переменных
(рассматриваемых как отдельные наборы одномерных данных)
и установлению зависимости между парами переменных (как
при анализе набора двумерных данных)

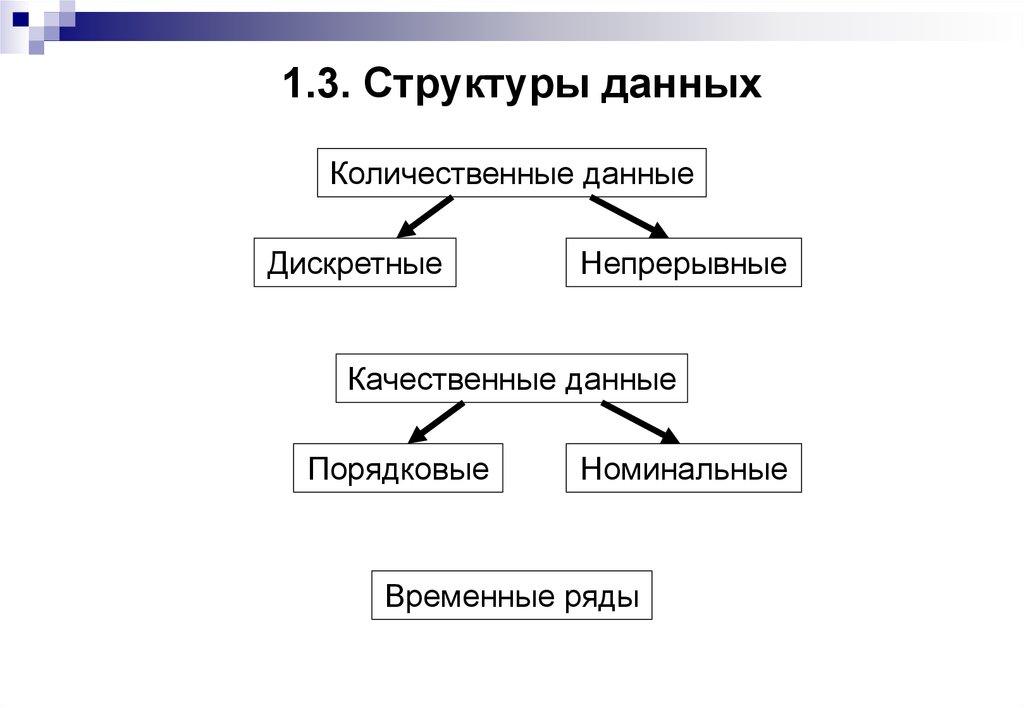
7. 1.3. Структуры данных

Количественные данные
Дискретные
Непрерывные
Качественные данные
Порядковые
Номинальные
Временные ряды

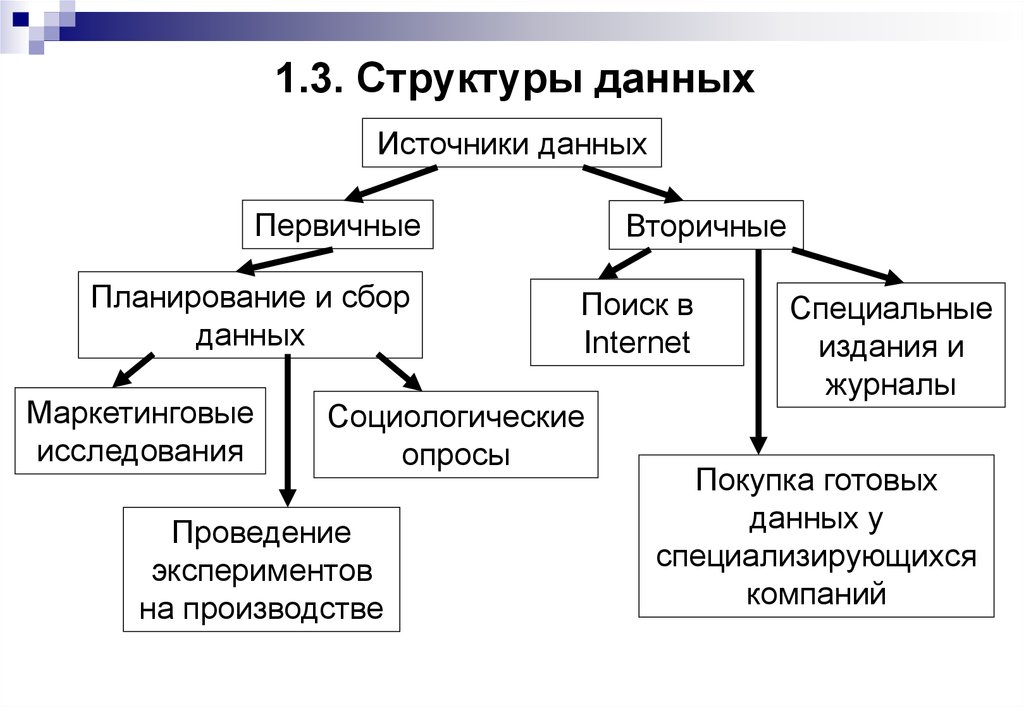
8. 1.3. Структуры данных

Источники данных
Первичные
Планирование и сбор
данных
Маркетинговые
исследования
Вторичные
Поиск в
Internet
Социологические
опросы
Проведение
экспериментов
на производстве
Специальные
издания и
журналы
Покупка готовых
данных у
специализирующихся
компаний

9. 1.4. Что такое переменная?

Переменная (английский термин variable) — это то, что можно
измерять, контролировать или чем можно манипулировать в
исследованиях. Иными словами, переменная — это то, что
варьируется, изменяется, а не является постоянным (от
английского корня var).
ПРИМЕРЫ: анкетные данные, систолическое давление
пациентов, количество лейкоцитов в крови, цена акций, товаров,
услуг, потребление, инвестиции, доход, государственные закупки
товаров и услуг, инструмент государственного регулирования (в
экономике); рейтинг программ, доля зрителей, количество
посещений сайта (в рекламе); скорость, температура, объем,
масса в (физике) и т. д.

10. 1.4. Что такое переменная?

Так как значения переменных не постоянны, нужно научиться
описывать их изменчивость.
Для этого
статистики.
придуманы
описательные
или
дескриптивные
Минимум и максимум — это минимальное и максимальное
значения переменной.
Среднее — сумма значений переменной, деленная на n (число
значений переменной).
Дисперсия и стандартное отклонение — наиболее часто
используемые меры изменчивости переменной. Дисперсия
меняется от нуля до бесконечности. Крайнее значение 0 означает
отсутствие изменчивости, когда значения переменной постоянны.

11. 1.4. Что такое переменная?

Медиана разбивает выборку на две равные части. Половина значений
переменной лежит ниже медианы, половина — выше.
Медиана дает общее представление о том, где сосредоточены значения
переменной, иными словами, где находится ее центр. В некоторых
случаях, например при описании доходов населения, медиана более
удобна, чем среднее.
Мода представляет собой максимально часто встречающееся значение
переменной (иными словами, наиболее «модное" значение переменной),
например популярная передача на телевидении, модный цвет платья или
марка автомобиля и т. д.
А так же есть еще множество других статистик: квартили, коэффициент
асимметрии, эксцесс, коэффициент корреляции и др.

12. 1.5. Основные законы распределения случайных величин и их назначение

Законы распределения случайных величин
служат
математическими
моделями
для
реальных объектов и явлений, что позволяет в
некоторых случаях применять их для расчетов и
анализа ситуации.

13. 1.5. Основные законы распределения случайных величин и их назначение

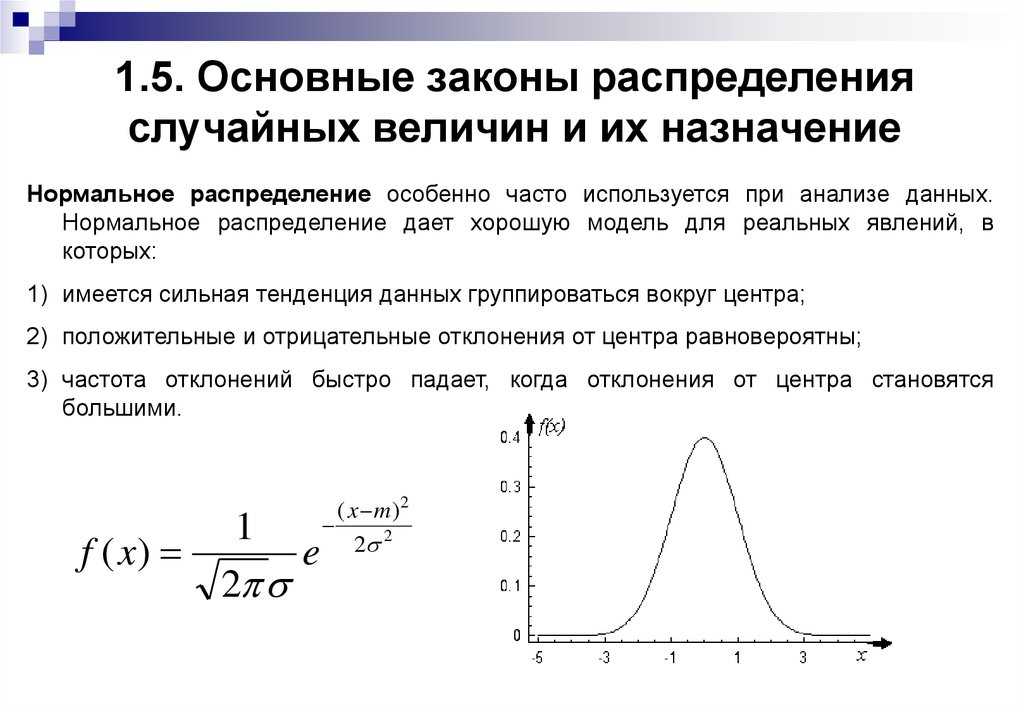
Нормальное распределение особенно часто используется при анализе данных.
Нормальное распределение дает хорошую модель для реальных явлений, в
которых:
1) имеется сильная тенденция данных группироваться вокруг центра;
2) положительные и отрицательные отклонения от центра равновероятны;
3) частота отклонений быстро падает, когда отклонения от центра становятся
большими.
1
f ( x)
e
2
( x m )2
2 2

14. 1.5. Основные законы распределения случайных величин и их назначение

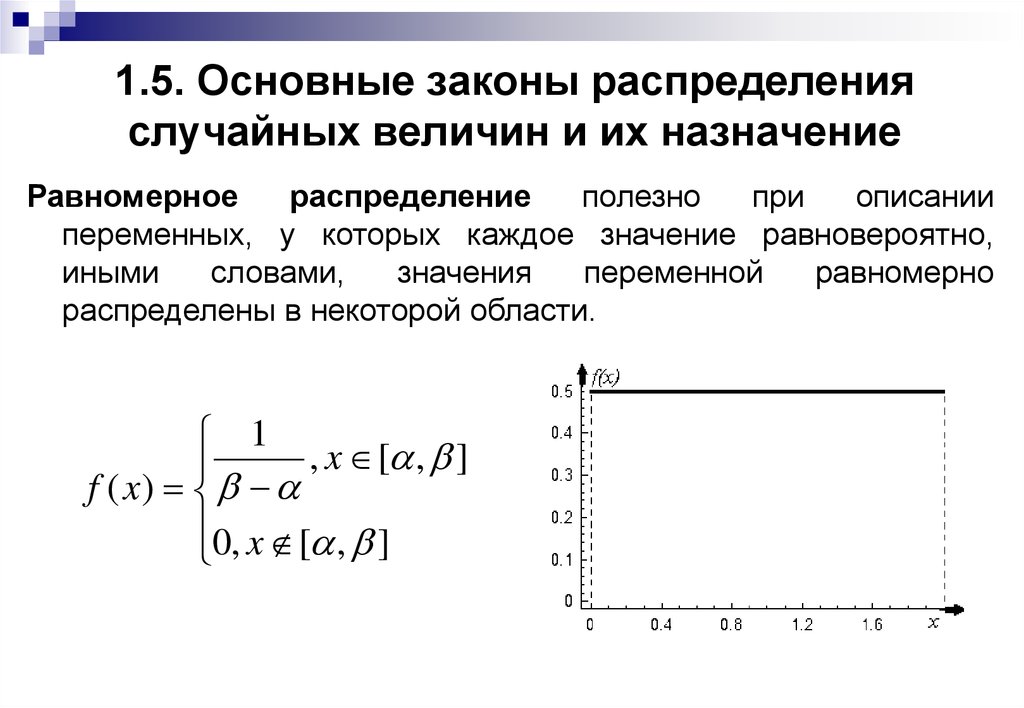
Равномерное
распределение
полезно
при
описании
переменных, у которых каждое значение равновероятно,
иными
словами,
значения
переменной
равномерно
распределены в некоторой области.
1
, x [ , ]
f ( x)
0, x [ , ]

15. 1.5. Основные законы распределения случайных величин и их назначение

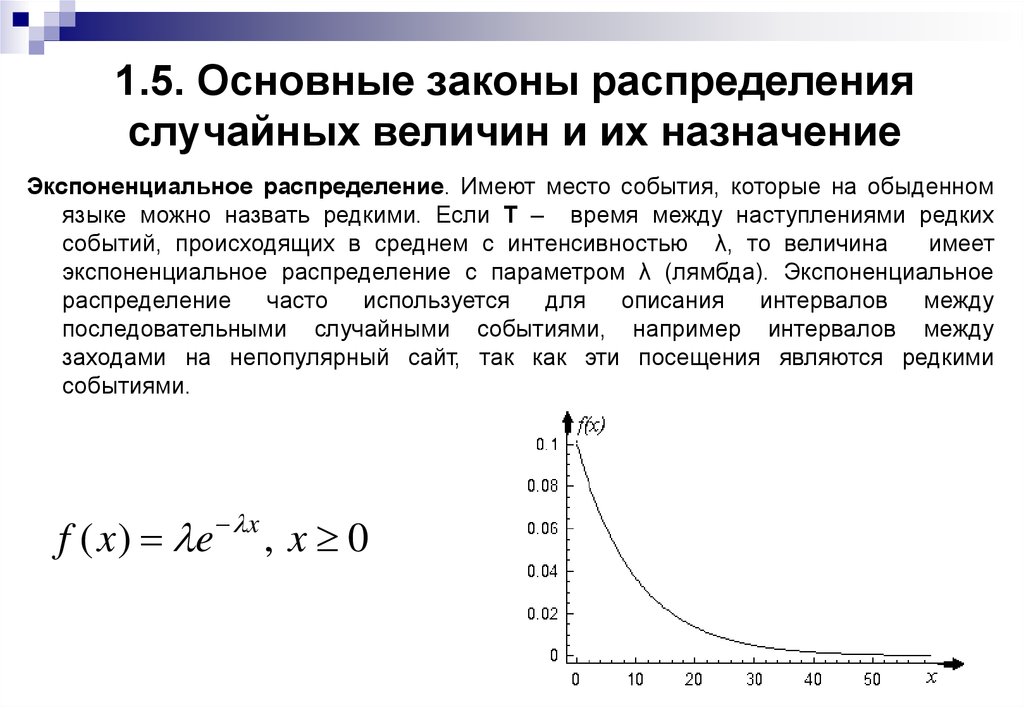
Экспоненциальное распределение. Имеют место события, которые на обыденном
языке можно назвать редкими. Если T – время между наступлениями редких
событий, происходящих в среднем с интенсивностью λ, то величина
имеет
экспоненциальное распределение с параметром λ (лямбда). Экспоненциальное
распределение часто используется для описания интервалов между
последовательными случайными событиями, например интервалов между
заходами на непопулярный сайт, так как эти посещения являются редкими
событиями.
f ( x ) e x , x 0

16. 1.5. Основные законы распределения случайных величин и их назначение

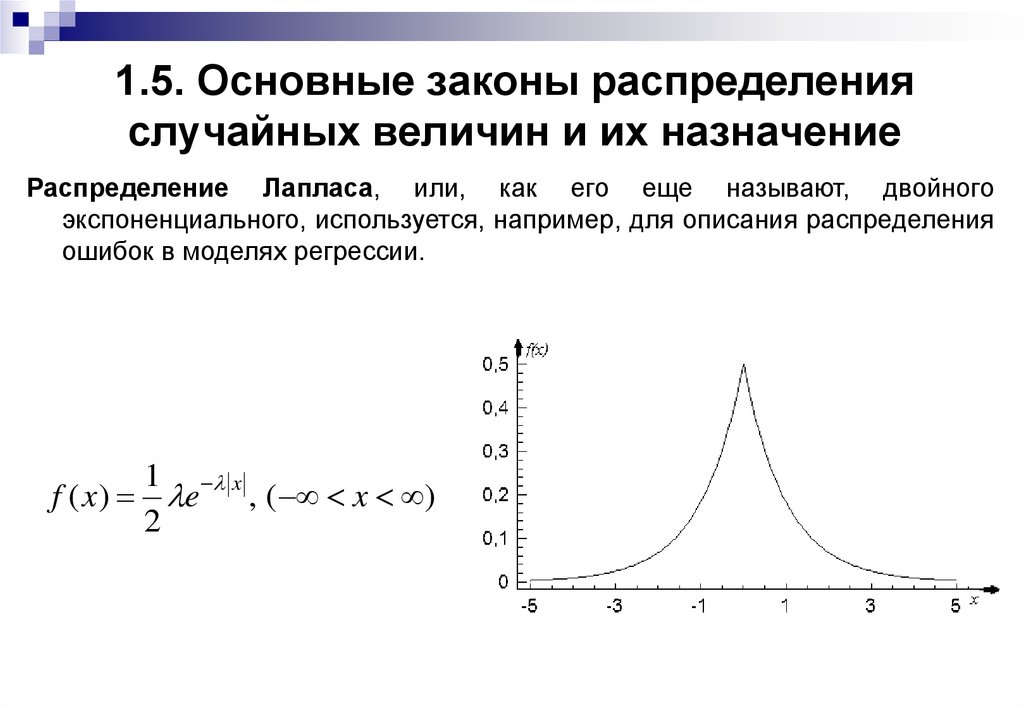
Распределение Лапласа, или, как его еще называют, двойного
экспоненциального, используется, например, для описания распределения
ошибок в моделях регрессии.
1 x
f ( x ) e , ( x )
2

17. 1.5. Основные законы распределения случайных величин и их назначение

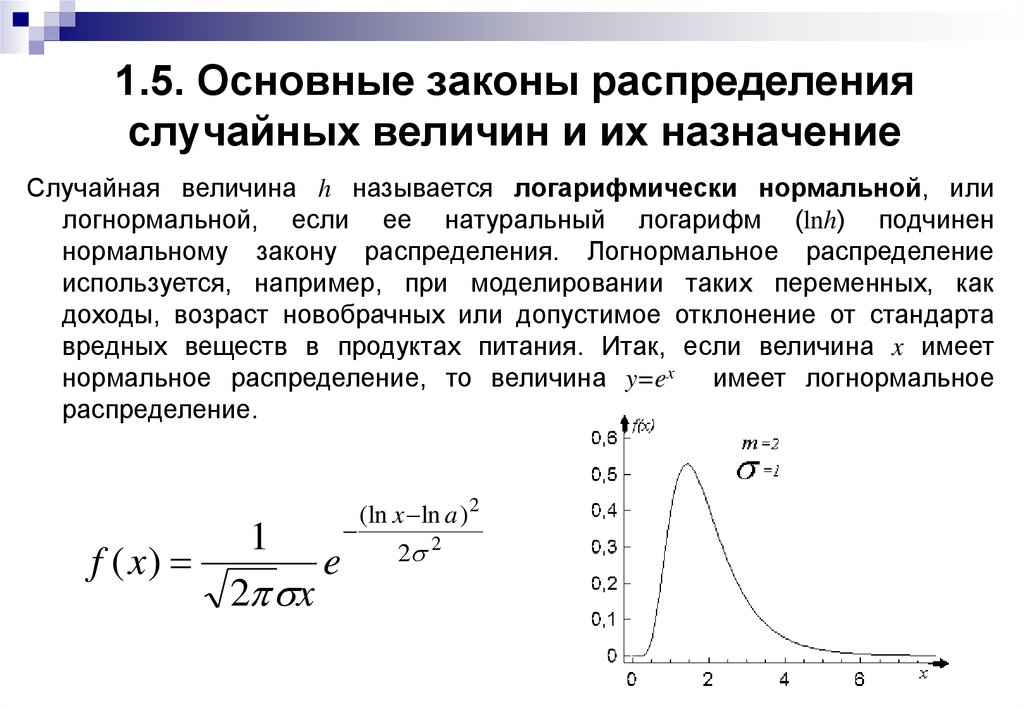
Случайная величина h называется логарифмически нормальной, или
логнормальной, если ее натуральный логарифм (lnh) подчинен
нормальному закону распределения. Логнормальное распределение
используется, например, при моделировании таких переменных, как
доходы, возраст новобрачных или допустимое отклонение от стандарта
вредных веществ в продуктах питания. Итак, если величина x имеет
нормальное распределение, то величина y=ex имеет логнормальное
распределение.
1
f ( x)
e
2 x
(ln x ln a ) 2
2 2

18. 1.5. Основные законы распределения случайных величин и их назначение

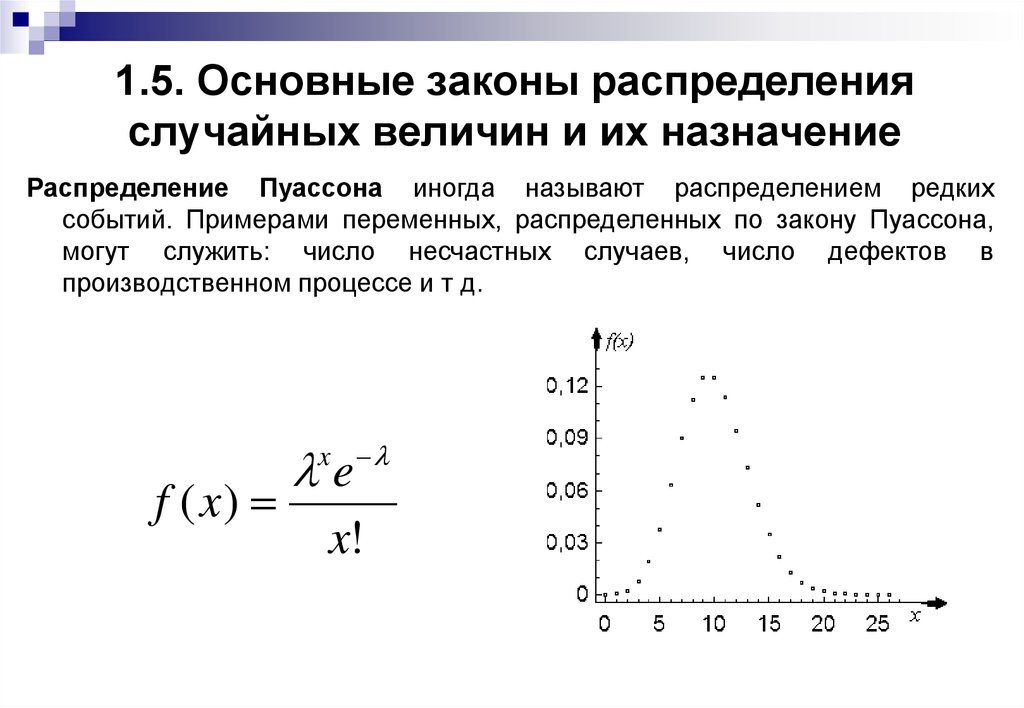
Распределение Пуассона иногда называют распределением редких
событий. Примерами переменных, распределенных по закону Пуассона,
могут служить: число несчастных случаев, число дефектов в
производственном процессе и т д.
f ( x)
x
e
x!

19. 1.6. Краткий обзор современных программных средств для проведения анализа данных.

MATLAB – это высокопроизводительный язык для технических
расчетов. Он включает в себя вычисления, визуализацию и
программирование в удобной среде, где задачи и решения
выражаются в форме, близкой к математической. Типичное
использование MATLAB – это:
• математические вычисления
• создание алгоритмов
• моделирование
• анализ данных, исследования и визуализация
• научная и инженерная графика
• разработка
интерфейса
приложений,
включая
создание
графического

20. 1.6. Краткий обзор современных программных средств для проведения анализа данных.

Mathcad – программное средство, среда для выполнения на
компьютере разнообразных математических и технических
расчетов, снабженная простым в освоении и в работе графическим
интерфейсом, которая предоставляет пользователю инструменты
для работы с формулами, числами, графиками и текстами.
В среде Mathcad доступны более сотни операторов и логических
функций, предназначенных для численного и символьного
решения математических задач различной сложности и
применения этих функций для анализа данных.

21. 1.6. Краткий обзор современных программных средств для проведения анализа данных.

STATISTICA – это универсальная интегрированная система,
предназначенная для статистического анализа и визуализации
данных,
управления
базами
данных
и
разработки
пользовательских приложений, содержащая широкий набор
процедур анализа для применения в научных исследованиях,
технике, бизнесе, а также специальные методы добычи данных.
С помощью реализованных в системе STATISTICA мощных языков
программирования, снабженных специальными средствами
поддержки, легко создаются законченные пользовательские
решения и встраиваются в различные другие приложения или
вычислительные среды.

22. 1.6. Краткий обзор современных программных средств для проведения анализа данных.

Deductor
Аналитическая платформа Deductor реализует практически все
современные подходы к анализу структурированной табличной
информации: хранилища данных (Data Warehouse), многомерный
анализ (OLAP), добыча данных (Data Mining), обнаружение знаний
в базах данных (Knowledge Discovery in Databases). Лучшим
способом изучить и понять целесообразность использования
современных технологий анализа - это испытать все на практике.

23. 1.6. Краткий обзор современных программных средств для проведения анализа данных.

STATGRAPHICS – это универсальный пакет для анализа и визуализации
данных. Отличительной особенностью пакета является наличие такого
инструмента как StatAdvisor, который помогает пользователям
интерпретировать полученные результаты, обеспечивает возможность
объединения в одном окне нескольких текстовых и графических подокон.
StatAdvisor дает пользователям понятные разъяснения полученных
результатов, определяет, являются ли эти результаты существенными, и
обращает особое внимание на любые возможные ошибки в анализе.
Пользователи получают немедленную интерпретацию результатов в
процедурах, доступных в как основной системе, так и в четырех
специальных модулях, поставляемых по выбору: Quality Control (контроль
качества), Experimental Design (планирование эксперимента), Time-Series
Analysis (анализ временных рядов) и Advanced Multivariate Method (анализ
вариаций).

24. Вопросы ?