Числовые характеристики дискретных случайных величин

1.

2.

А) Математическое ожидание постоянной величины
равно ей самой
M(C) = C, C – постоянная.
Б) Постоянный множитель можно выносить за знак
математического ожидания
M(C•X) = C•M(X).
В) Математическое ожидание суммы / разности
случайных величин равно сумме / разности их
математических ожиданий M(X±Y) = M(X) ±M(Y).
Г). Математическое ожидание произведения
независимых случайных величин равно произведению
их математических ожиданий
M(X•Y) = M(X) • M(Y), если X и Y независимы.

3.

А) Какая из таблиц не задает закон
распределения случайной величины?
Объясните почему.
x
p
0
1
2
3
0,1 0,5 0,1 0,3
x
p
1
2
3
4
0,3 0,1 0,3 0,2
x
p
–1 1
2
3
0,1 0,2 0,3 0,4

4.

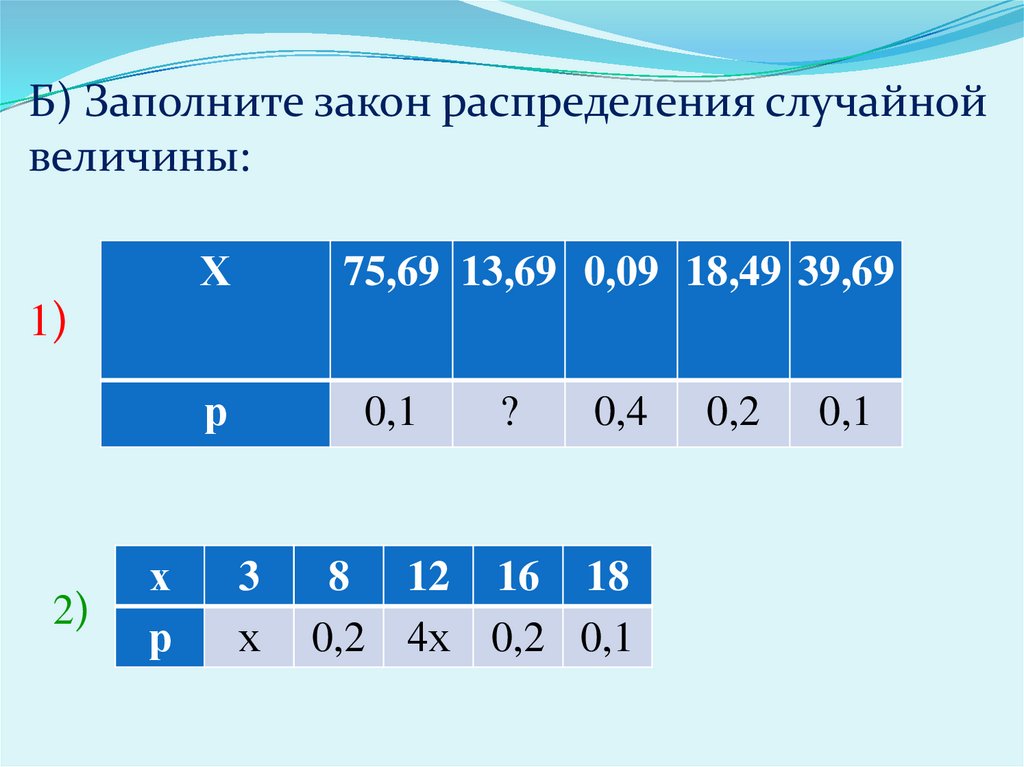
Б) Заполните закон распределения случайной
величины:
Х
75,69 13,69 0,09 18,49 39,69
р
0,1
1)
2)
х
р
3
х
?
0,4
8 12 16 18
0,2 4х 0,2 0,1
0,2
0,1

5.

Первая группа
Распределение вероятностей случайной величины X
задана следующим образом
х
1
2
3
4
р
0,4 0,3 0,2 0,1
Найдите математическое ожидание случайной величины:
М(5Х); М(3Х + 5); М(2Х – 3).
Вторая группа
Распределение вероятностей случайной величины X
задана следующим образом
х
3
4
5
6
р
0,4 0,3 0,2 0,1
Найдите математическое ожидание случайной величины:
М(4Х); М(2Х + 7); М(3Х – 5).

6.

Первая группа.
1) М(Х) = 1 · 0,4 + 2 · 0,3 + 3 · 0,2 + 4 · 0,1 = 0,4 +
0,6 + 0,6 + 0,4 = 2
М(5Х) = 5М(Х) = 10;
М(3Х + 5) = 3М(Х) + 5 = 11;
М(2Х – 3) = 2М(Х) – 3 = 1.
Вторая группа.
2) М(Х) = 3 · 0,4 + 4 · 0,3 + 5 · 0,2 + 6 · 0,1 = 1,2 +
1,2 + 1 + 0,6 = 4
М(4Х) = 4М(Х) = 16;
М(2Х + 7) = 2М(Х) + 7 = 15;
М(3Х – 5) = 3М(Х) – 5 = 7.

7.

Задача.
Страна экспортирует раков на зарубежные рынки.
Покупатели готовы платить высокие цены, когда
раки прибывают живыми. Если X - число смертей
на дюжину раков, распределение вероятностей для
X определяется следующим образом
x
px
0
1
0,54 0,26
2
3
0,15 а
4
5
6
0,01 0,01 0,001
Найдите:
А) значение а.
Б) В течение длительного периода, каково среднее
число смертей на дюжину раков?

8.

а = 1 – (0,54 + 0,26 + 0,15 + 0,01+ 0,01 + 0,01 =
0,02
М(Х) = 0 · 0,54 + 1 · 0,26 + 2·0,15 + 3 · 0,02 + 4 ·
0,01 + 5 · 0,01 + 6 · 0,01 = 0 + 0,26 + 0,06 + 0,04 +
0,05 + 0,06 = 0,47
Ответ: А) 0,02;
Б) 0,47.

9.

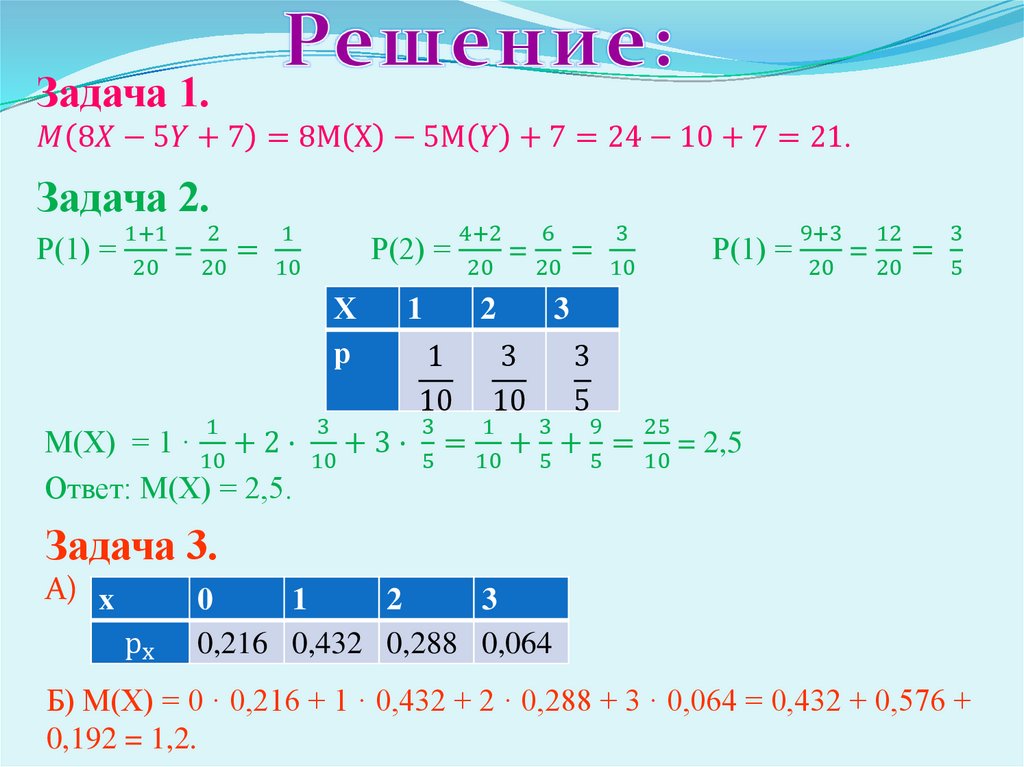
Задача 1.
Известны математические ожидания случайных величин: