Соотношения между сторонами и углами треугольника

1. Соотношения между сторонами и углами треугольника

СООТНОШЕНИЯ МЕЖДУ
СТОРОНАМИ
И УГЛАМИ ТРЕУГОЛЬНИКА
7 класс
Учитель: Паутова Ольга Николаевна

2. Решите задачу

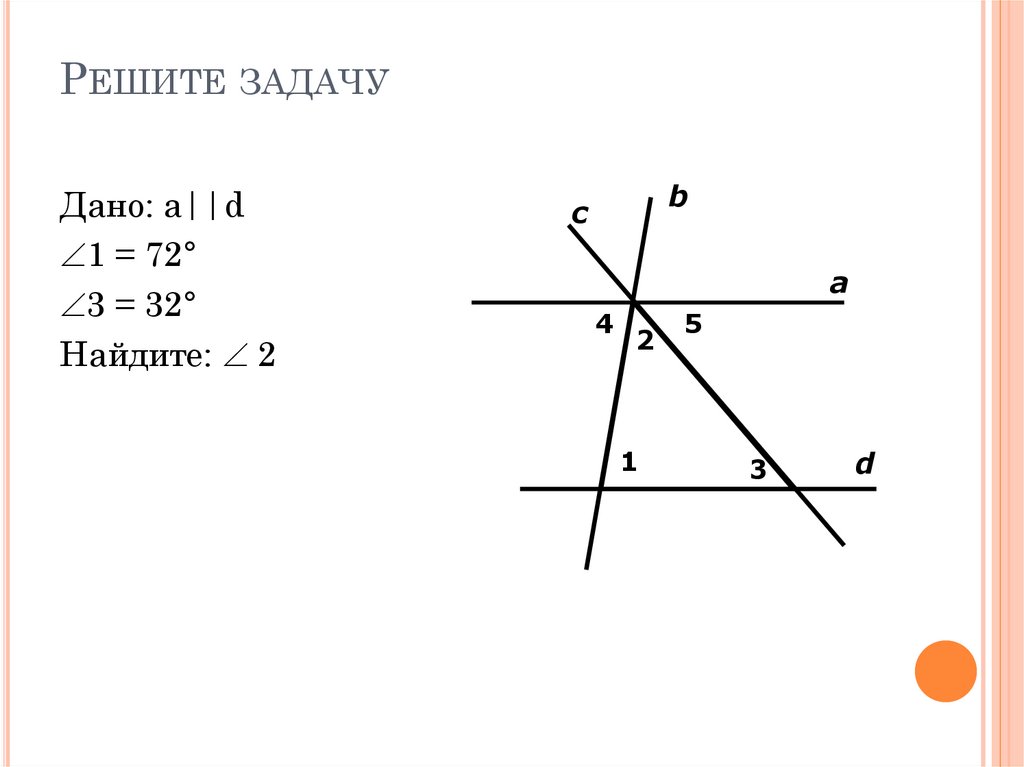
РЕШИТЕ ЗАДАЧУ
Дано: а||d
1 = 72°
3 = 32°
Найдите: 2
b
c
а
4
2
1
5
3
d

3. Сумма углов треугольника

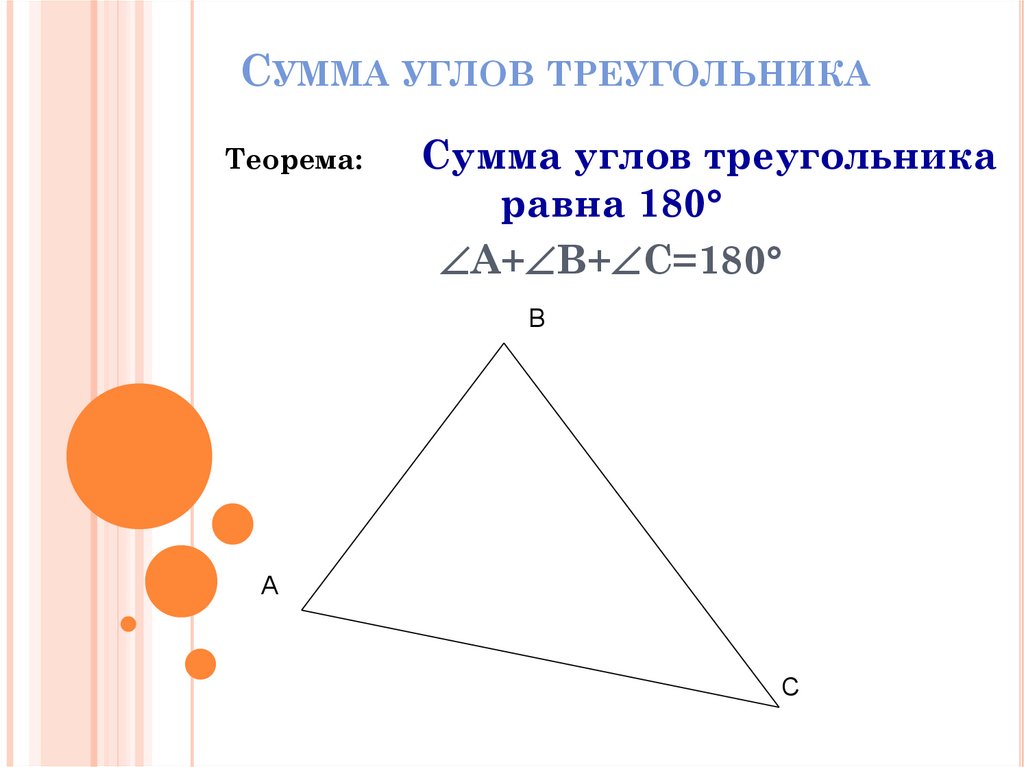
СУММА УГЛОВ ТРЕУГОЛЬНИКА
Теорема:
Сумма углов треугольника
равна 180
А+ В+ С=180
В
А
С

4.

а
В
4
Дано:
5
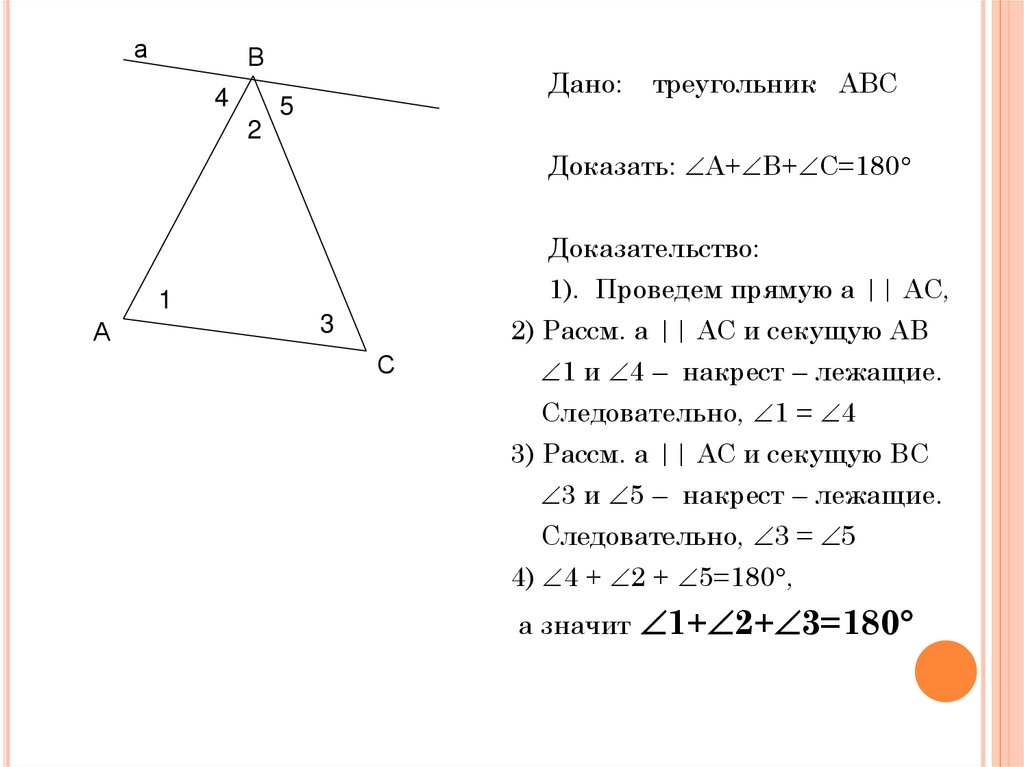
треугольник АВС
2
Доказать: А+ В+ С=180
Доказательство:
1). Проведем прямую а || АС,
1
А
2) Рассм. а || АС и секущую АВ
3
С
1 и 4 – накрест – лежащие.
Следовательно, 1 = 4
3) Рассм. а || АС и секущую ВС
3 и 5 – накрест – лежащие.
Следовательно, 3 = 5
4) 4 + 2 + 5=180 ,
а значит 1+ 2+ 3=180

5. Задачи

ЗАДАЧИ
А
В
70
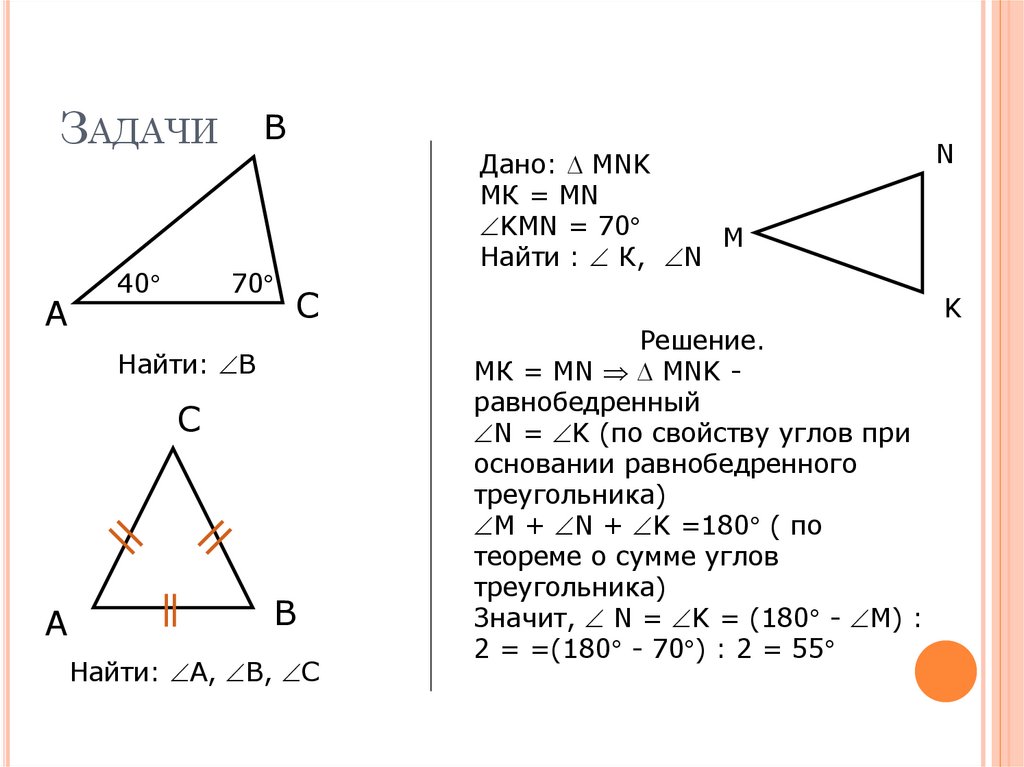
Дано: MNK
МК = MN
KMN = 70
М
Найти : К, N
40
С
Найти: В
С
А
В
Найти: А, В, С
N
K
Решение.
МК = MN MNK равнобедренный
N = K (по свойству углов при
основании равнобедренного
треугольника)
M + N + K =180 ( по
теореме о сумме углов
треугольника)
Значит, N = K = (180 - M) :
2 = =(180 - 70 ) : 2 = 55

6. Задачи

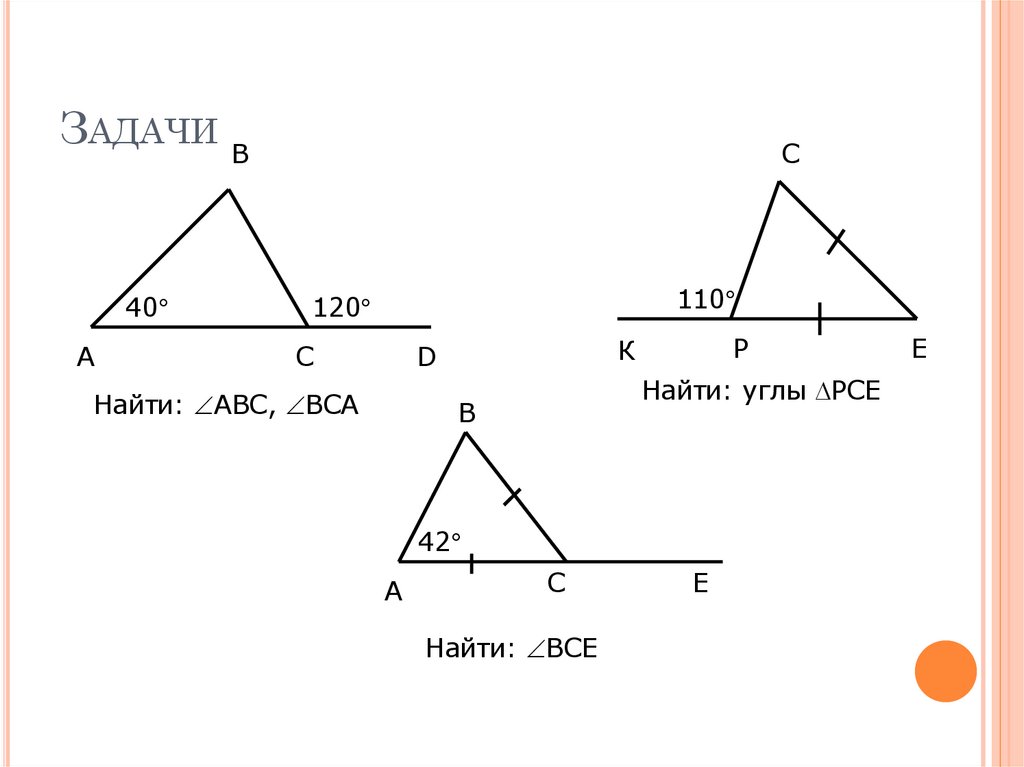
ЗАДАЧИ В
40
А
С
110
120
С
Найти: АВС, ВСА
Р
К
D
Найти: углы РСЕ
В
42
А
С
Найти: ВСЕ
Е
Е

7. ВНЕШНИЙ УГОЛ

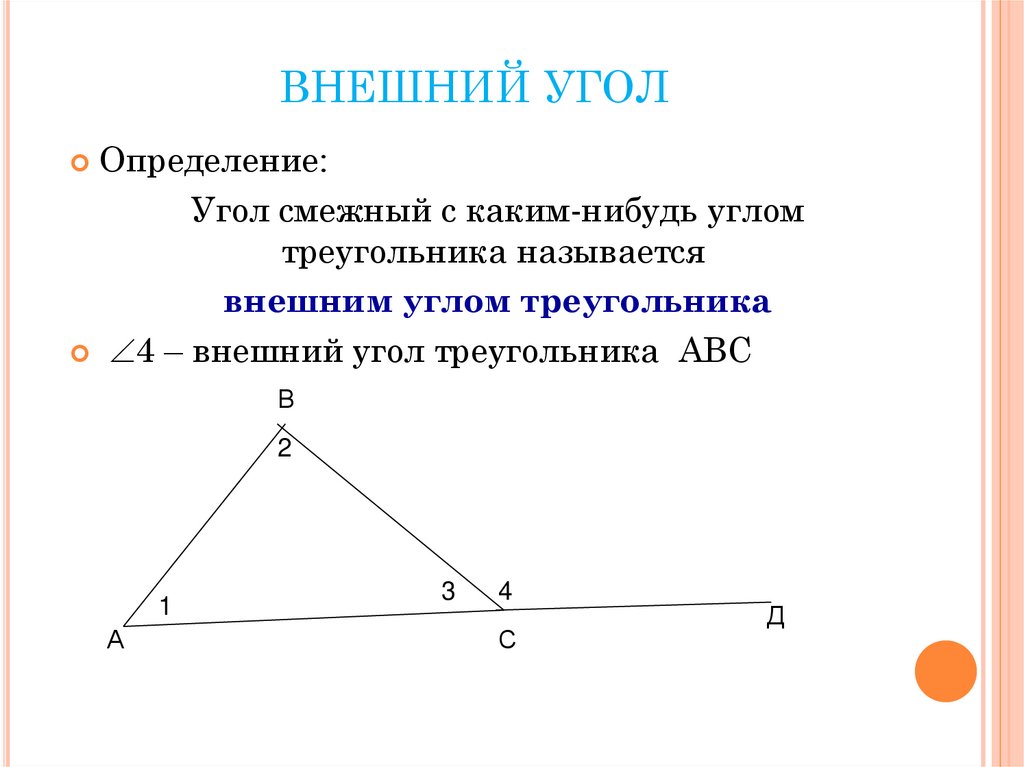
Определение:
Угол смежный с каким-нибудь углом
треугольника называется
внешним углом треугольника
4 – внешний угол треугольника АВС
В
2
1
А
3
4
С
Д

8. Свойство внешнего угла

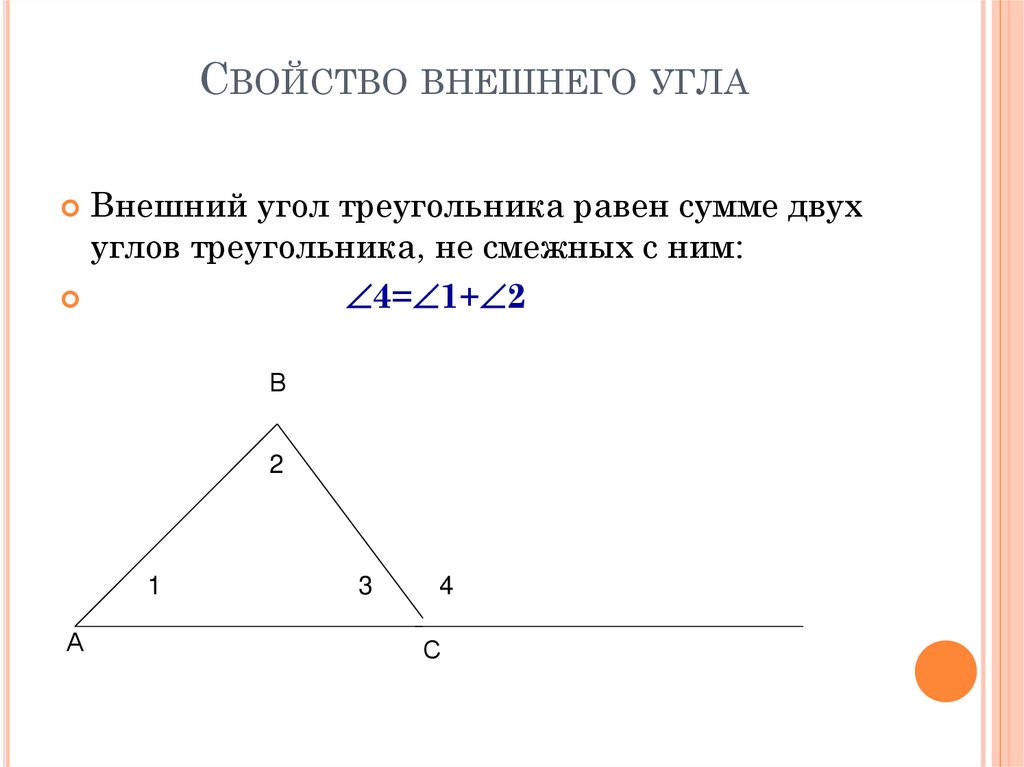
СВОЙСТВО ВНЕШНЕГО УГЛА
Внешний угол треугольника равен сумме двух
углов треугольника, не смежных с ним:
4= 1+ 2
В
2
1
А
3
4
С

9. Задача: Решите задачу, используя свойство внешнего угла треугольника

ЗАДАЧА:
РЕШИТЕ ЗАДАЧУ, ИСПОЛЬЗУЯ СВОЙСТВО
ВНЕШНЕГО УГЛА ТРЕУГОЛЬНИКА
Решение:
В
130
А
С
Найти: углы АВС
Е
1. ВСЕ = А + В (по свойству
внешнего угла треугольника)
2. ВС=АС АВС равнобедренный (по опред.)
Значит,
А = С = ВСЕ : 2 =
130 : 2 = 65
3. ВСА =180 - ВСЕ (смежные)
ВСА =180 - 130 =50
Ответ: А = С = 65 ,
ВСА = 50 .

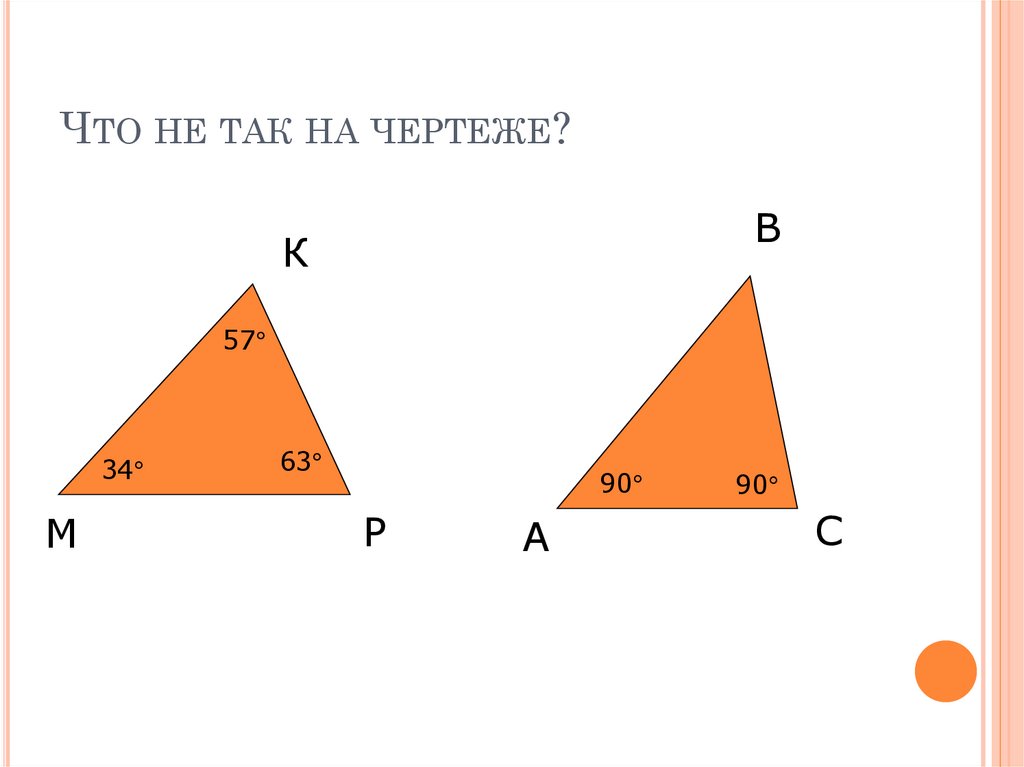
10. Что не так на чертеже?

ЧТО НЕ ТАК НА ЧЕРТЕЖЕ?
В
К
57
34
М
63
90
Р
А
90
С

11. ВИДЫ ТРЕУГОЛЬНИКОВ

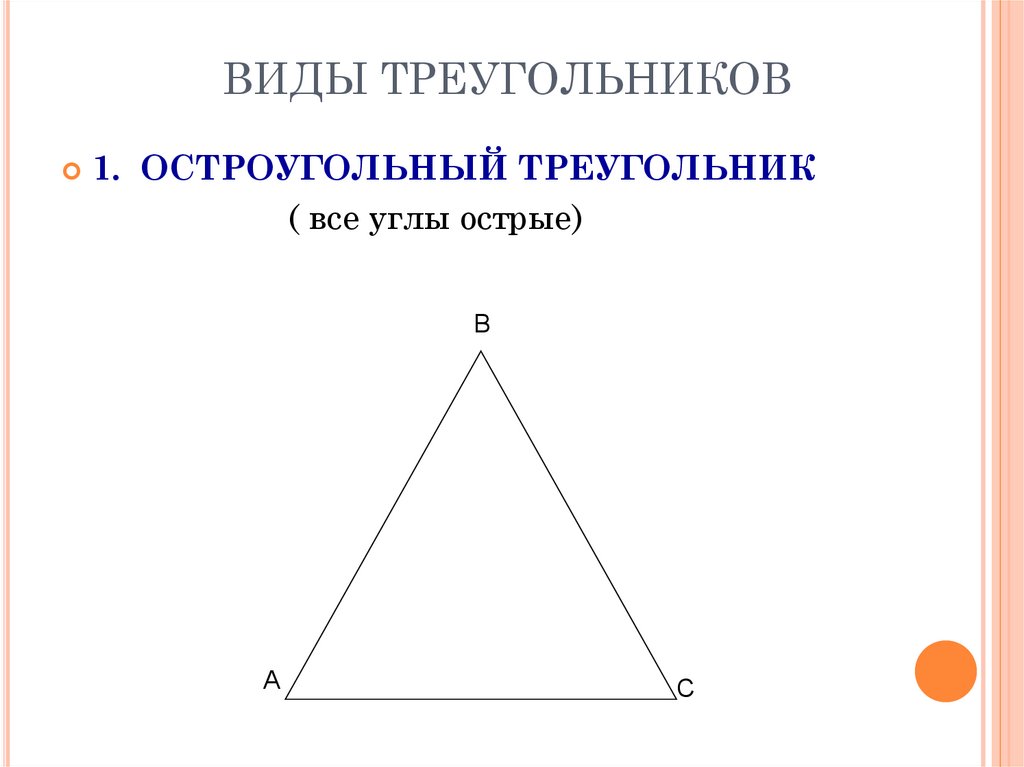
1.
ОСТРОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
( все углы острые)
В
А
С

12. ВИДЫ ТРЕУГОЛЬНИКА

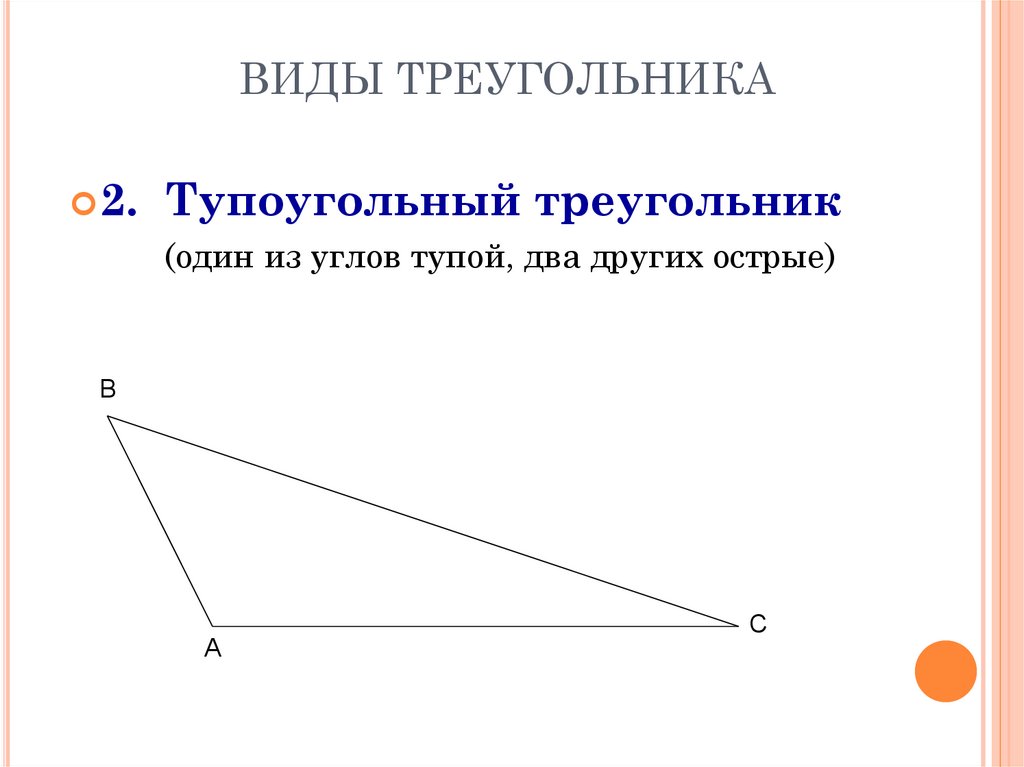
2.
Тупоугольный треугольник
(один из углов тупой, два других острые)
В
А
С

13. ВИДЫ ТРЕУГОЛЬНИКА

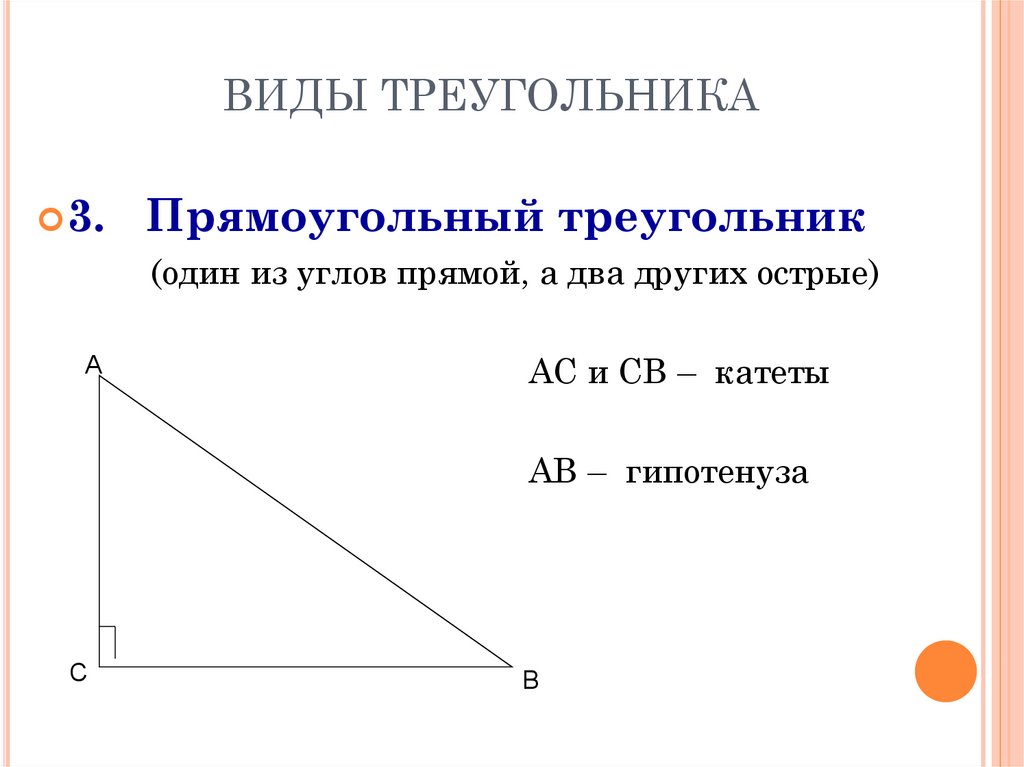
3.
Прямоугольный треугольник
(один из углов прямой, а два других острые)
А
АС и СВ – катеты
АВ – гипотенуза
С
В

14. Виды треугольников

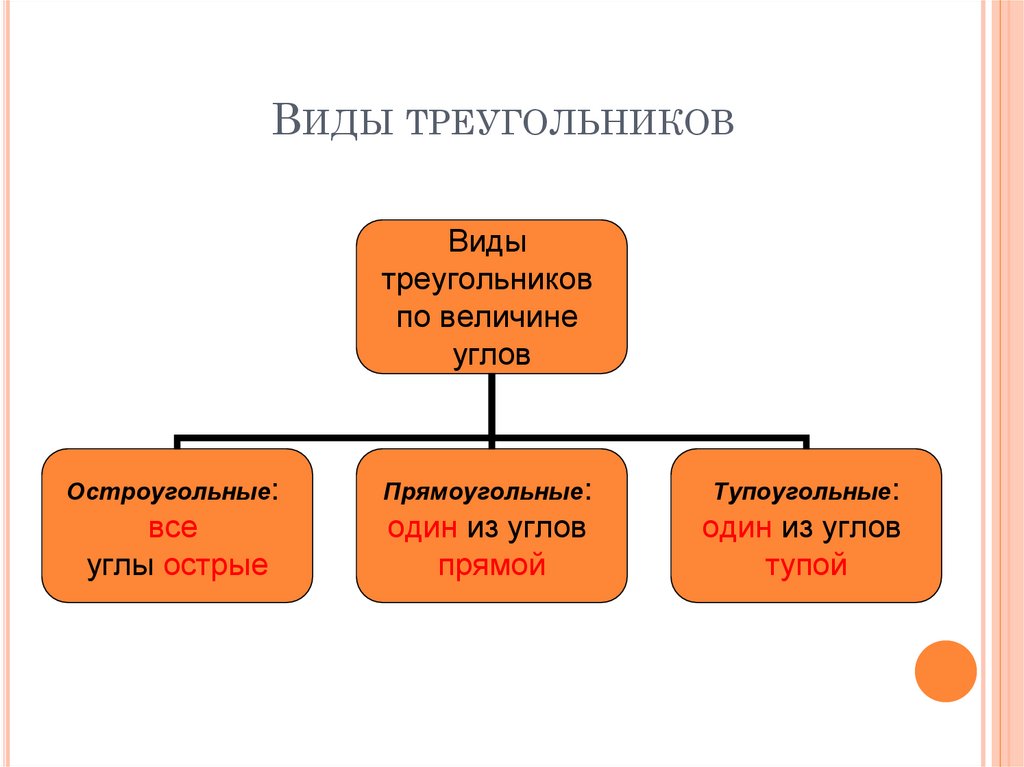
ВИДЫ ТРЕУГОЛЬНИКОВ
Виды
треугольников
по величине
углов
Остроугольные:
Прямоугольные:
Тупоугольные:
все
углы острые
один из углов
прямой
один из углов
тупой

15. Соотношения между сторонами и углами треугольника

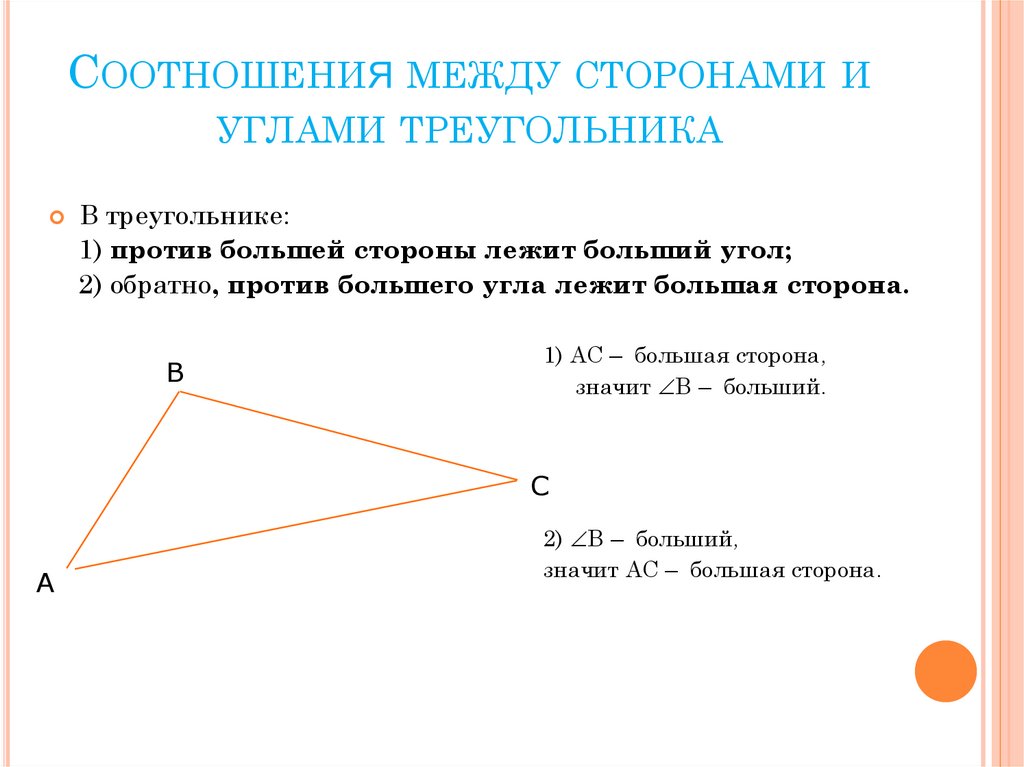
СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И
УГЛАМИ ТРЕУГОЛЬНИКА
В треугольнике:
1) против большей стороны лежит больший угол;
2) обратно, против большего угла лежит большая сторона.
В
1) АС – большая сторона,
значит В – больший.
С
А
2) В – больший,
значит АС – большая сторона.

16. СЛЕДСТВИЯ

1. В прямоугольном треугольнике
гипотенуза больше катета.
Признак равнобедренного треугольника:
2. Если в треугольнике два угла равны,
то треугольник равнобедренный

17. НЕРАВЕНСТВО ТРЕУГОЛЬНИКА

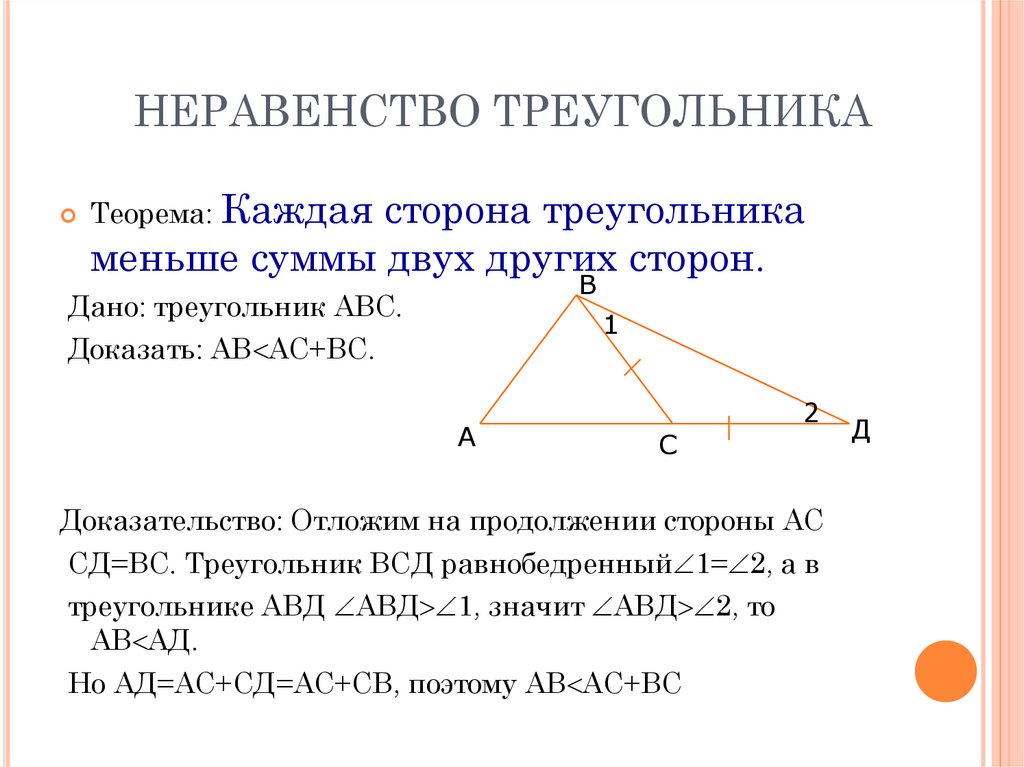
Каждая сторона треугольника
меньше суммы двух других сторон.
Теорема:
В
Дано: треугольник АВС.
Доказать: АВ АС+ВС.
1
А
2
С
Доказательство: Отложим на продолжении стороны АС
СД=ВС. Треугольник ВСД равнобедренный 1= 2, а в
треугольнике АВД АВД 1, значит АВД 2, то
АВ АД.
Но АД=АС+СД=АС+СВ, поэтому АВ АС+ВС
Д

18. СЛЕДСТВИЕ

ДЛЯ ЛЮБЫХ ТРЁХ ТОЧЕК
А, В И С, не лежащих
на одной прямой,
справедливы неравенства:
АВ АС+ВС;
АС АВ+ВС;
ВС ВА+АС.