Number Systems

1.

Number
Systems
Understanding Different Number Systems and Their Conversion to Decimal

2.

Introduction
This presentation explores various number systems and methods for converting
them to the decimal system.

3.

01
Overview

4.

Definition of Number Systems
Number systems are ways of expressing numbers
with a consistent set of digits and rules. The most
common include decimal (base 10), binary (base 2),
octal (base 8), and hexadecimal (base 16). Each
system has unique applications in computing,
mathematics, and digital electronics.

5.

Importance of Number Systems
Understanding number systems is crucial for fields such as computer science and
engineering. Different systems serve various purposes, such as efficient data storage
(binary), user-friendly representation (decimal), or compact information display
(hexadecimal). Mastery of conversions between these systems is essential for
software development, programming, and digital communication.

6.

Types of Number Systems
The main types of number systems include:
1. **Decimal (Base 10)**: The standard system used in daily life, consisting of digits from 0 to 9.
2. **Binary (Base 2)**: Used in computers, consisting of only two digits, 0 and 1. Every bit in binary represents an
exponential value of 2.
3. **Octal (Base 8)**: Utilizes digits from 0 to 7. It is often used in computing to simplify binary representations
into a more manageable form.
4. **Hexadecimal (Base 16)**: Combines digits from 0 to 9 and letters A to F. This system is widely used in
programming and digital design because it is more concise than binary.

7.

02
Conversion
Methods

8.

Binary to Decimal Conversion
To convert a binary number to decimal, multiply each bit by 2 raised to the power of
its position (from right to left, starting at 0) and sum the results. For example, the
binary number 1011:
- 1*(2^3) + 0*(2^2) + 1*(2^1) + 1*(2^0) = 8 + 0 + 2 + 1 = 11 in decimal.

9.

Hexadecimal to Decimal
Conversion
To convert a hexadecimal number to decimal, multiply
each digit by 16 raised to the power of its position
(from right to left, starting at 0). For example, the
hexadecimal number 2F3:
- 2*(16^2) + F*(16^1) + 3*(16^0) = 2*256 + 15*16 +
3*1 = 512 + 240 + 3 = 755 in decimal.

10.

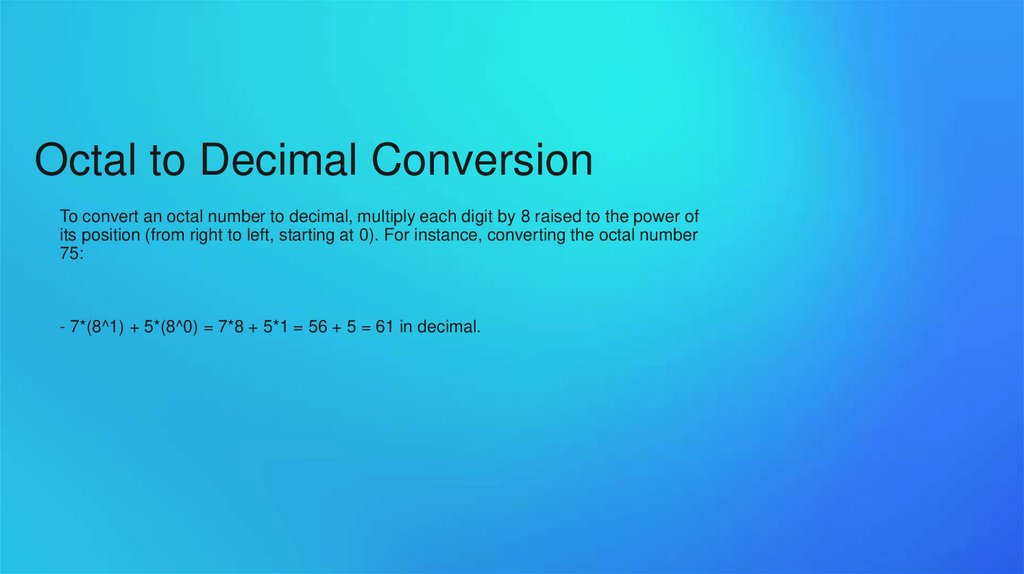
Octal to Decimal Conversion
To convert an octal number to decimal, multiply each digit by 8 raised to the power of
its position (from right to left, starting at 0). For instance, converting the octal number
75:
- 7*(8^1) + 5*(8^0) = 7*8 + 5*1 = 56 + 5 = 61 in decimal.

11.

Conclusions
Mastering number systems and their conversions is
vital for effective problem-solving in technology and
engineering fields. This presentation provided insights
into the importance of understanding different number
systems and the methods for converting binary, octal,
and hexadecimal values to decimal.

12.

Thank you!
Do you have any questions?
CREDITS: This presentation template was created by Slidesgo,
and includes icons, infographics & images by Freepik
+
9
1
6
2
0
4
2
1
8
3
8