Similar presentations:
Основные свойства уравнения
1.
1. Выразите неизвестное учерез х:
2х + у=11; у=11-2х;
3х – у=9;
у=3х-9;
х-у=5;
у=х-5;
2х + 2у=6;
у=3-х;
2. 2. Основные свойства уравнения. (вставьте пропущенные слова)
* 2. Основные свойствауравнения.
(вставьтеСвойство
пропущенные
слова)
1.
Любой член уравнения можно __________ из
одной части уравнения в другую, изменив его
____на _________________.
Свойство 2.
Обе части уравнения можно __________или
__________ на одно и то же число, не равное
_____.
3. 2. Основные свойства уравнения. (вставьте пропущенные слова)
* 2. Основные свойствауравнения.
(вставьтеСвойство
пропущенные
слова)
1.
Любой член уравнения можно переносить из
одной части уравнения в другую, изменив его
знак на противоположный.
Свойство 2.
Обе части уравнения можно умножить или
разделить на одно и то же число, не равное
нулю.
4.
yy
3
2
1
1
0
-1
-1
1
x
0
-1-1
-2
-3
1
x
5.
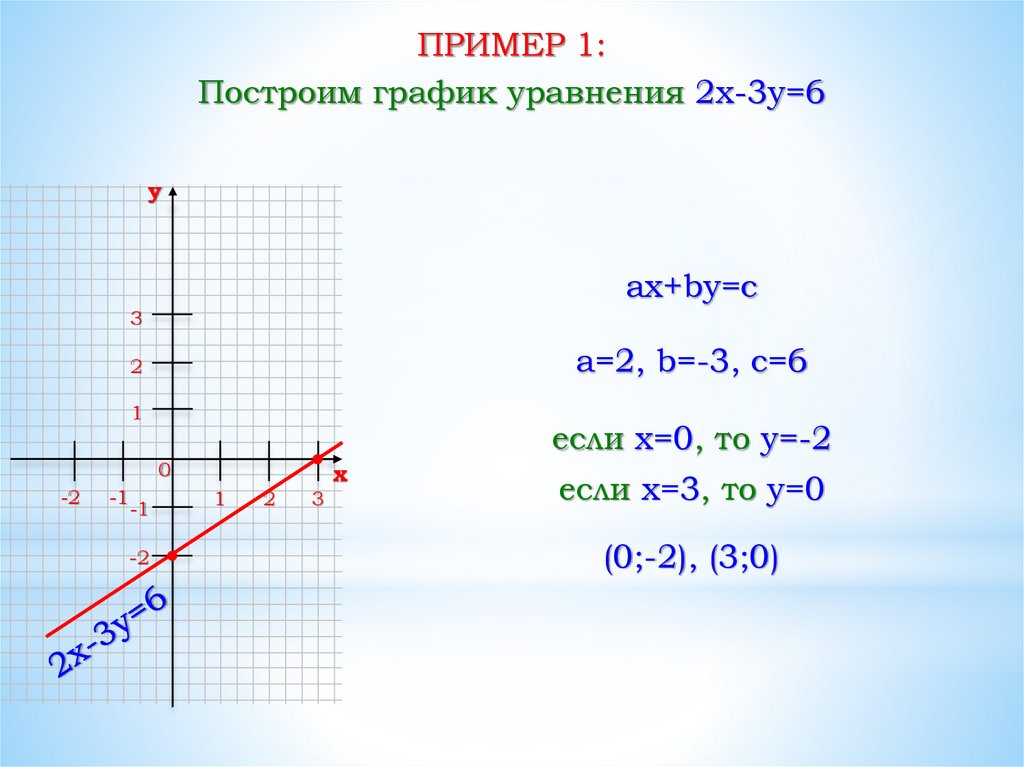
ПРИМЕР 1:Построим график уравнения 2x-3y=6
y
ax+by=c
3
a=2, b=-3, c=6
2
1
если x=0, то y=-2
0
-2
-1
-1
-2
1
x
2
3
если x=3, то y=0
(0;-2), (3;0)
6.
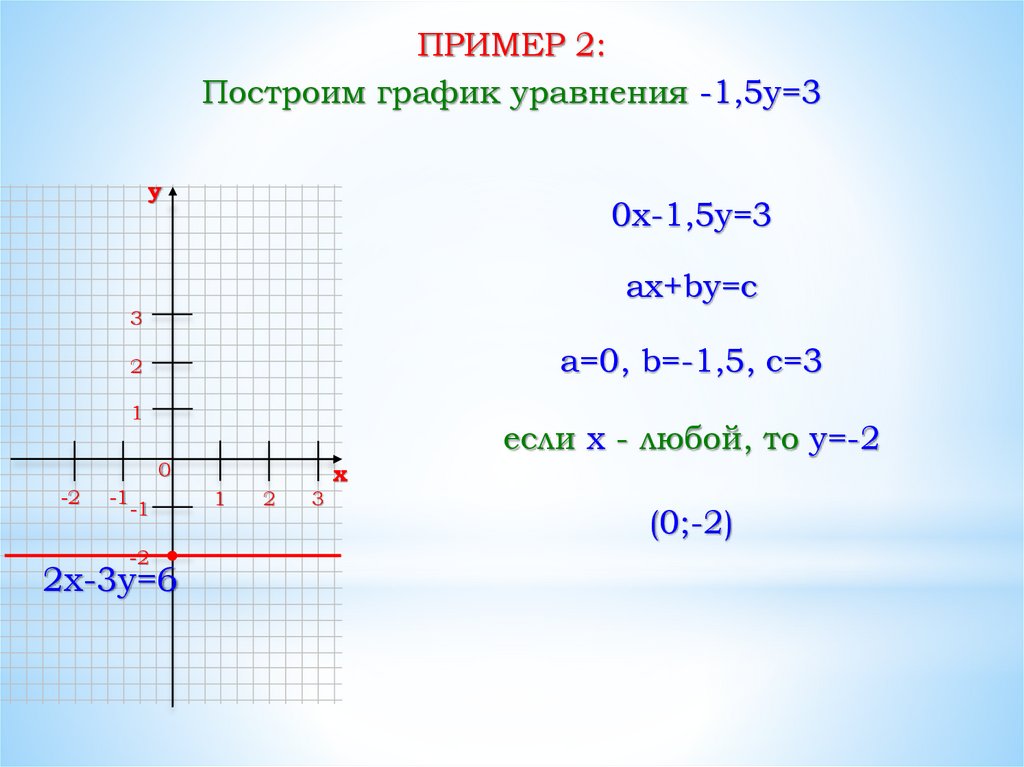
ПРИМЕР 2:Построим график уравнения -1,5y=3
y
0x-1,5y=3
ax+by=c
3
a=0, b=-1,5, c=3
2
1
если x - любой, то y=-2
0
-2
-1
-1
-2
2x-3y=6
1
x
2
3
(0;-2)
7.
ПРИМЕР 3:Построим график уравнения 1 x=1
3
y
1x=1
3
1
x+0y=1
3
3
2
ax+by=c
1
0
-2
-1
-1
1
x
2
3
1
a= , b=0, c=1
3
(3;0)
-2
Игорь Жаборовский
UROKIMATEMATIKI.RU
8.
9.
Решением системы уравнений сдвумя переменными называется
пара значений переменных (x;y),
обращающая каждое уравнение
системы в верное равенство.
Решить систему уравнений – значит
найти все её решения или доказать,
что решений нет.
10.
Системы уравненийГрафический
способ
Метод
подстановки
Аналитический
способ
Метод
сложения
Метод
замены пере
менной
11. Метод подстановки
1. Выразить из какого-нибудь уравнения системы однупеременную через другую.
2. Подставить в другое уравнение системы вместо этой
переменной полученное выражение.
3. Решить получившееся уравнение с одной переменной.
4. Найти соответствующее значение второй переменной.
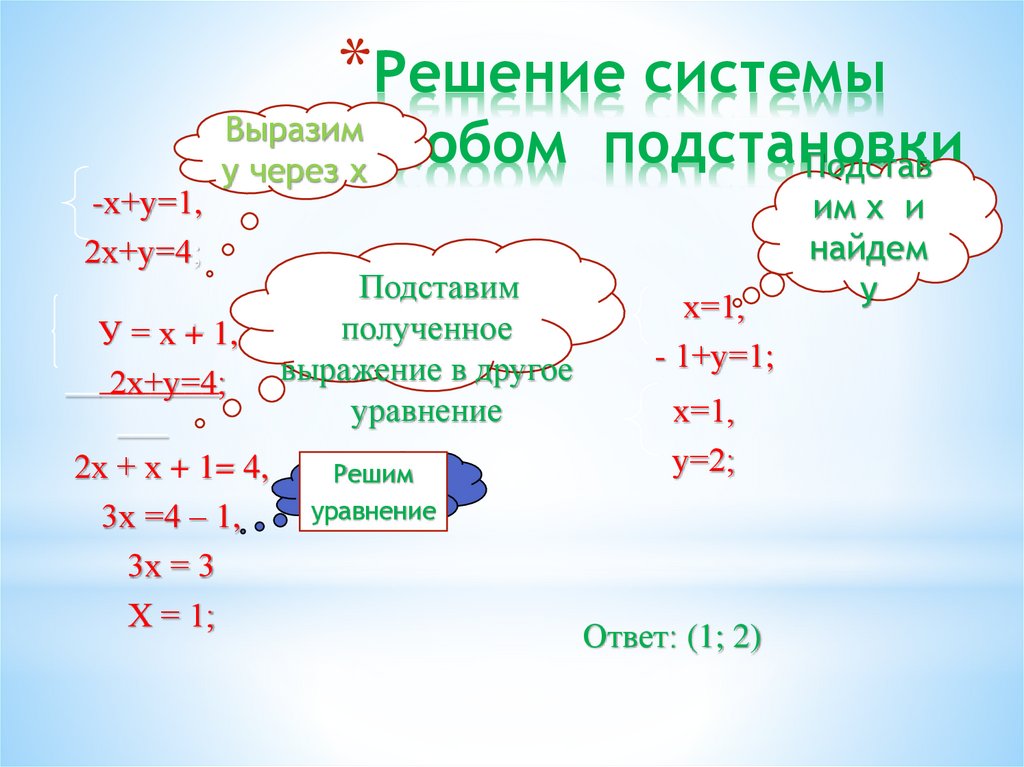
12. Решение системы способом подстановки
*Решение системыспособом подстановки
Подстав
Выразим
у через х
-х+у=1,
2х+у=4;
У = х + 1,
_________
2х+у=4;
___
2х + х + 1= 4,
3х =4 – 1,
3х = 3
Х = 1;
Подставим
полученное
выражение в другое
уравнение
Решим
уравнение
х=1,
- 1+у=1;
х=1,
у=2;
Ответ: (1; 2)
им х и
найдем
у
13. Алгоритм решения систем уравнений способом подстановки.
* Алгоритм решения системуравнений способом
подстановки.
*выразить из любого уравнения системы
одну переменную через другую;
*подставить полученное выражение вместо
этой переменной в другое уравнение
системы
*решить полученное уравнение с одной
переменной;
*найти соответствующее значение второй
переменной.
14.
Задание 1x²+y²+3xy =-1,
x+2y= 0;
Какой из учеников применил метод подстановки
наиболее рационально?
a) x²=-y²-3xy-1, б) x²+y²+3xy =-1,
x+2y= 0;
2y=-x;
в) x²+y²+3xy =-1,
x=-2y.
15.
1.Умножьте почленно уравнения системы, подбирая
множители так, чтобы коэффициенты при одной из
переменных стали противоположными числами.
2.
Сложите почленно левые и правые части
уравнений системы.
3.
Решите получившееся уравнение с одной
переменной.
4.
Найдите соответствующее значение второй
переменной.
16.
Задание 2+
x²-2y² =14,
x²+2y²= 18;
2x² =32,
x² =16,
x =4;
Можно ли записывать ответ?
17. Алгоритм решения систем уравнений способом сложения.
* Алгоритм решения системуравнений способом
сложения.
*умножить почленно уравнения системы, подбирая
множители так, чтобы коэффициенты при одной из
переменных стали противоположными числами;
*сложить почленно левые и правые части
уравнений системы;
*решить получившееся уравнение с одной
переменной;
*найти соответствующее значение второй
переменной.
18.
1.Построить график функции, заданной первым
уравнением системы.
2.
Построить график функции, заданной вторым
уравнением системы.
3.
Определить координаты точек пересечения
графиков функций.
19.
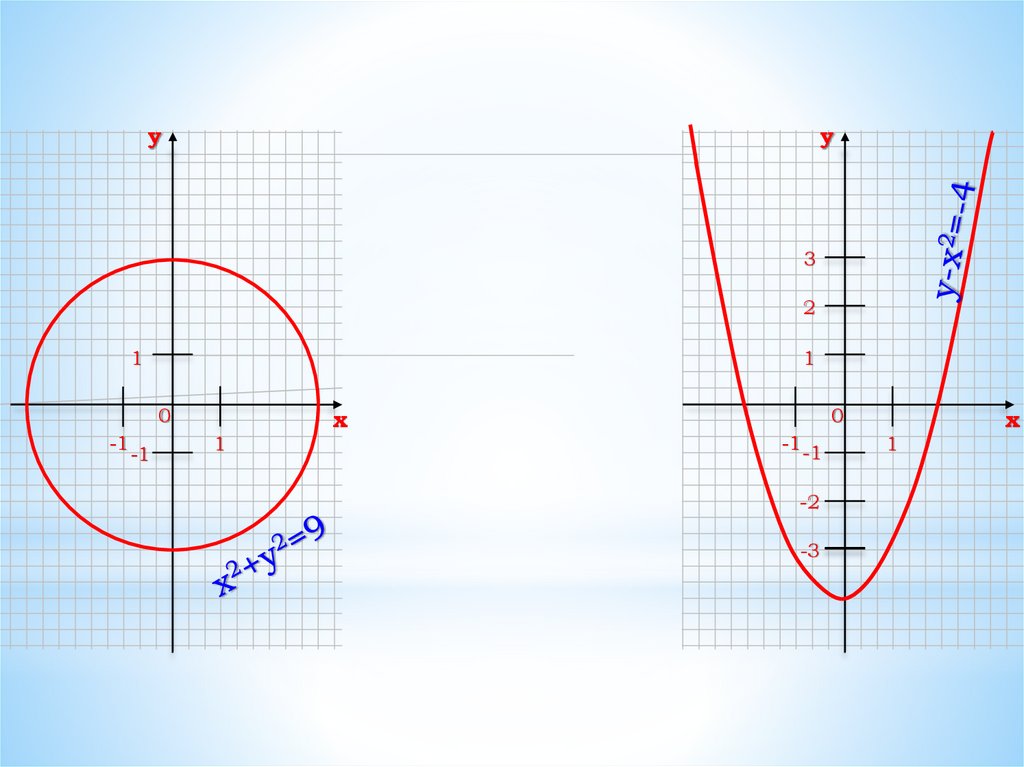
Задание 3На рисунке изображена парабола и три прямые.
Укажите систему уравнений, которая не имеет решений.
у
у х2 1
А.
х у 3
у 10 0
у х2 1
у х2 1
Б .
х 5 0
у х 1
В.
у 10 0
2
0
х
х 5 0
Г.Все три системы
х у 3
20.
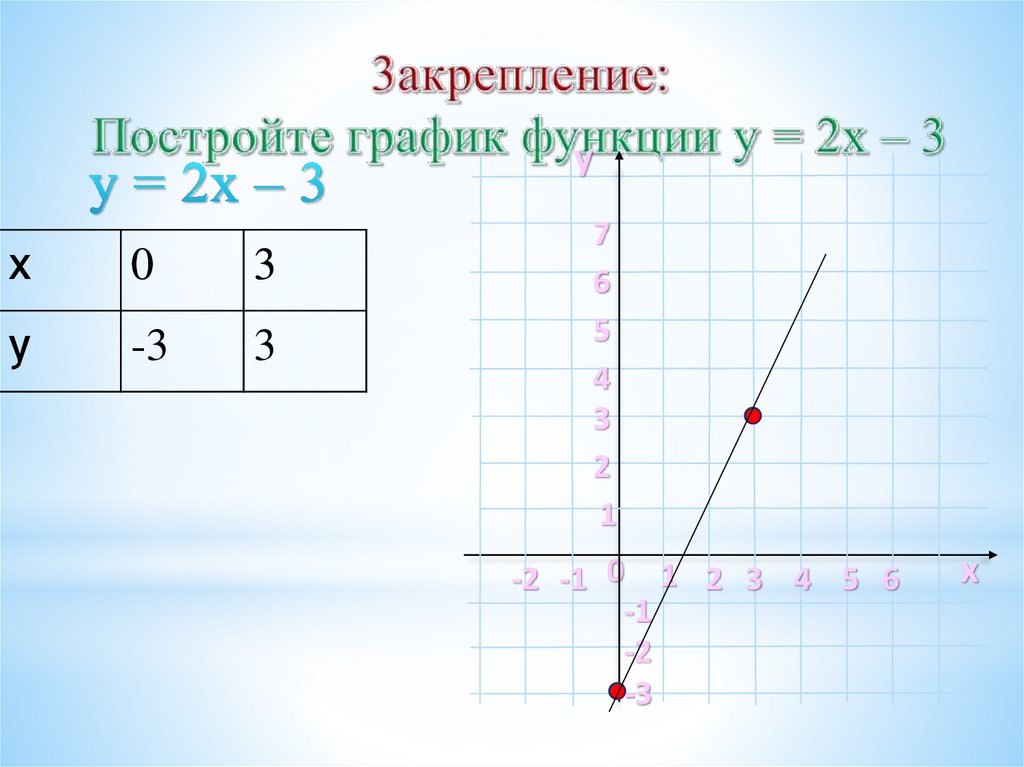
ух
0
3
у
-3
3
7
6
5
4
3
2
1
-2 -1 0 1 2 3 4 5 6
-1
-2
-3
х
21.
Самостоятельная работа:Решить систему уравнений
2х+у=11,
3х-у=9;
5х-2у=6,
7х+2=6;
х+2у=5,
2х-у=5;
х+3у=6,
2х+у=7;
22.
Итог урока:Сделай вывод
Методы решения
Графический
Подстановки
Сложения
Преимущества
Недостатки
23.
Сделай выводМетоды решения
Преимущества
Недостатки
Графический
Наглядность
Громоздкость,
неточность
Подстановки
Точный
Трудоемкие
выкладки
Сложения
Точный
В выборе
множителя
24.
Рефлексия:Стратегия «Смайлики»
Кратко написать самое важное, что
уяснил с урока и приклеить на
смайлик. Стикеры

















 mathematics
mathematics








