Similar presentations:
Системы линейных уравнений. Основные понятия
1.
2.
«Мне приходится делить время между политикой иуравнениями. Однако уравнение, по-моему,гораздо
важнее. Политика существует только для данного
момента, а уравнения будут существовать вечно».
А. Эйнштейн
3.
Дорогу осилитидущий, а
математику –
мыслящий.
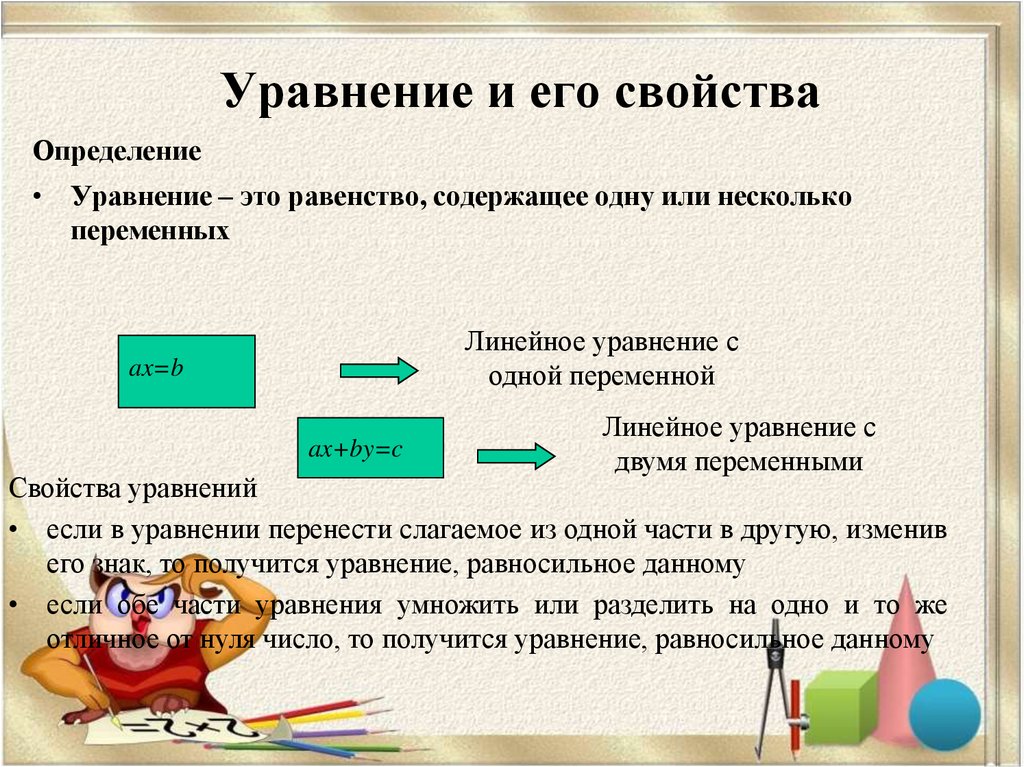
4. Уравнение и его свойства
Определение• Уравнение – это равенство, содержащее одну или несколько
переменных
Линейное уравнение с
одной переменной
ax=b
ax+by=c
Линейное уравнение с
двумя переменными
Свойства уравнений
• если в уравнении перенести слагаемое из одной части в другую, изменив
его знак, то получится уравнение, равносильное данному
• если обе части уравнения умножить или разделить на одно и то же
отличное от нуля число, то получится уравнение, равносильное данному
5.
ЗНАКОМТЕСЬ..........Системой уравнений называется некоторое количество
уравнений, объединенных фигурной скобкой. Фигурная
скобка означает, что все уравнения должны выполняться
одновременно .
Решением системы уравнений с двумя
переменными называется пара значений
переменных, обращающая каждое
уравнение системы в верное равенство.
6. Система линейных уравнений с двумя неизвестными
Сумма двух чисел равна 12, а разностьравна 2. Найдите эти числа
Пусть x – первое число, а y – второе число,
тогда:
Сумма чисел равна: x + y = 12
Разность чисел равна: x – y = 2
7. Система линейных уравнений с двумя неизвестными
Пара значений x = 7 и y = 5 являютсярешением данной системы.
8.
9. Работа в классе
10.
СПОСОБЫ РЕШЕНИЙ СИСТЕМЛИНЕЙНЫХ УРАВНЕНИЙ
Системы линейных уравнений
Графический
способ
Способ
подстановки
Способ
сложения
11.
ГРАФИЧЕСКИЙ СПОСОБВыразим переменную
у через х в каждом
уравнении
Построим графики
всех получившихся
линейных функций
Найдем координаты
точек пересечения
12.
Графический способ (алгоритм)Выразить у через х в каждом уравнении
Построить в одной системе координат график
каждого уравнения
Определить координаты точки пересечения
Записать ответ: х=…; у=… , или (х; у)
13. Решение системы графическим способом
Выразим учерез х
у - х=2,
у+х=10;
y
y=x+2
10
у=х+2,
у=10-х;
Построим график
первого уравнения
6
у=х+2
х
у
0
-2
2
0
y=10 - x
2
1
Построим график у=10 - х
второго уравнения
х
0
у
10
-2
0
1
10
0
Ответ: (4; 6)
4
10
x
14.
Сколько решений имеет система?a)
2х + у = -3,
3х + у = 1
y = -2x-3,
у = -3x+1
б)
2у =4x+8,
-2х + у = 1
y = 2x+4,
у = 2x+1
в)
2х – 2у = 1,
6х – 6у = 3
y=х – 0.5,
y=х – 0.5
15. Способ сравнения (алгоритм)
• Выразить у через х (или х через у) в каждомуравнении
• Приравнять выражения, полученные для
одноимённых переменных
• Решить полученное уравнение и найти
значение одной переменной
• Подставить значение найденной переменной
в одно из выражений для другой переменной и
найти её значение
• Записать ответ: х=…; у=… .
16. Решение системы способом сравнения
у - 2х=4,7х - у =1;
у=2х+4,
7х - 1= у;
Выразим у через х
Приравняем
выражения
для у
у=2·1+4,
х=1;
7х - 1=2х+4,
7х - 2х=4+1,
5х=5
,х=1.
у=2х+4,
х=1;
Решим
уравнение
у=6,
х=1.
Ответ: (1; 6)
Подставим
17.
СПАСИБО ЗАВНИМАНИЕ !
















 mathematics
mathematics








