Кручение. Тема 2.5

1.

КОМИТЕТ ОБРАЗОВАНИЯ И НАУКИ КУРСКОЙ ОБЛАСТИ
ОБПОУ «Железногорский горно-металлургический колледж»
Комиссия общепрофессиональных дисциплин
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
учебный раздел в курсе технической механики
Преподаватель технической механики Шепелева Е.В.
11

2. Сопротивление материалов

ТЕМА 2.5
КРУЧЕНИЕ
1. Внутренние силовые факторы
2. Эпюры крутящих моментов
2
2

3. Кручение

Кручением
называется
вид
деформации,
при
которой
в
поперечном сечении бруса возникает
только один внутренний силовой
фактор - крутящий момент Мz.
3

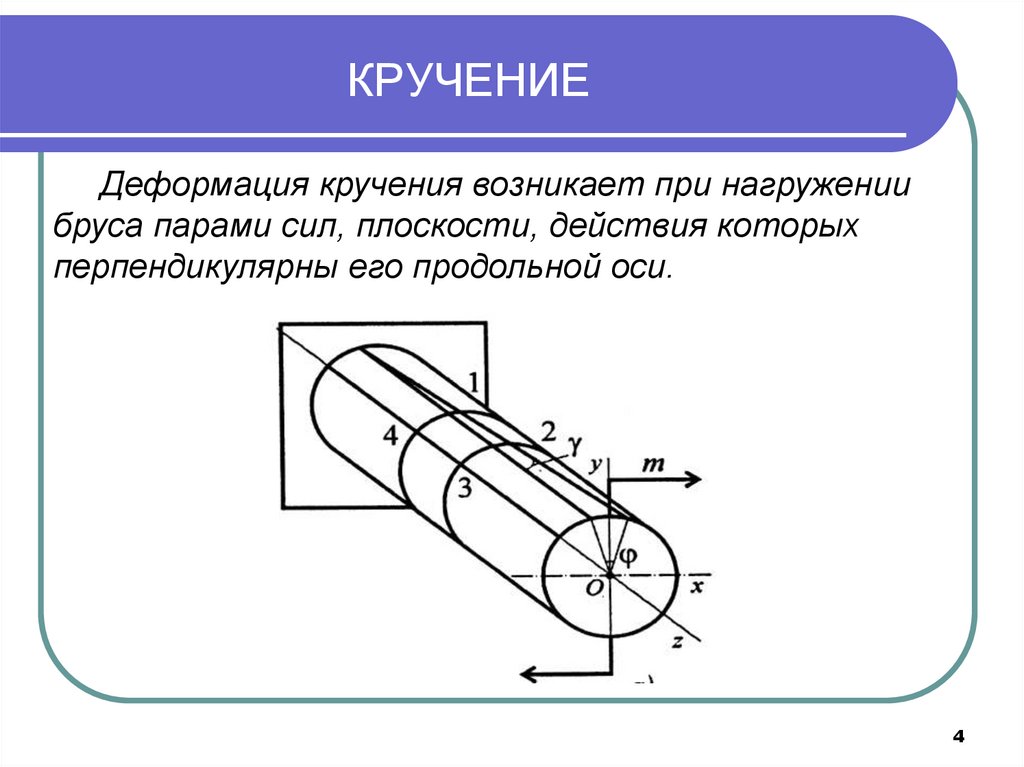
4. КРУЧЕНИЕ

Деформация кручения возникает при нагружении
бруса парами сил, плоскости, действия которых
перпендикулярны его продольной оси.
4

5. ГИПОТЕЗЫ ПРИ КРУЧЕНИИ

1. Выполняется гипотеза плоских сечений.
2. Радиус, проведенный из центра поперечного
сечения бруса, не искривляется.
3. Расстояния между поперечными сечениями
после деформации не меняются.
4. Ось бруса не искривляется. Диаметры
поперечных сечений не меняются.
5

6.

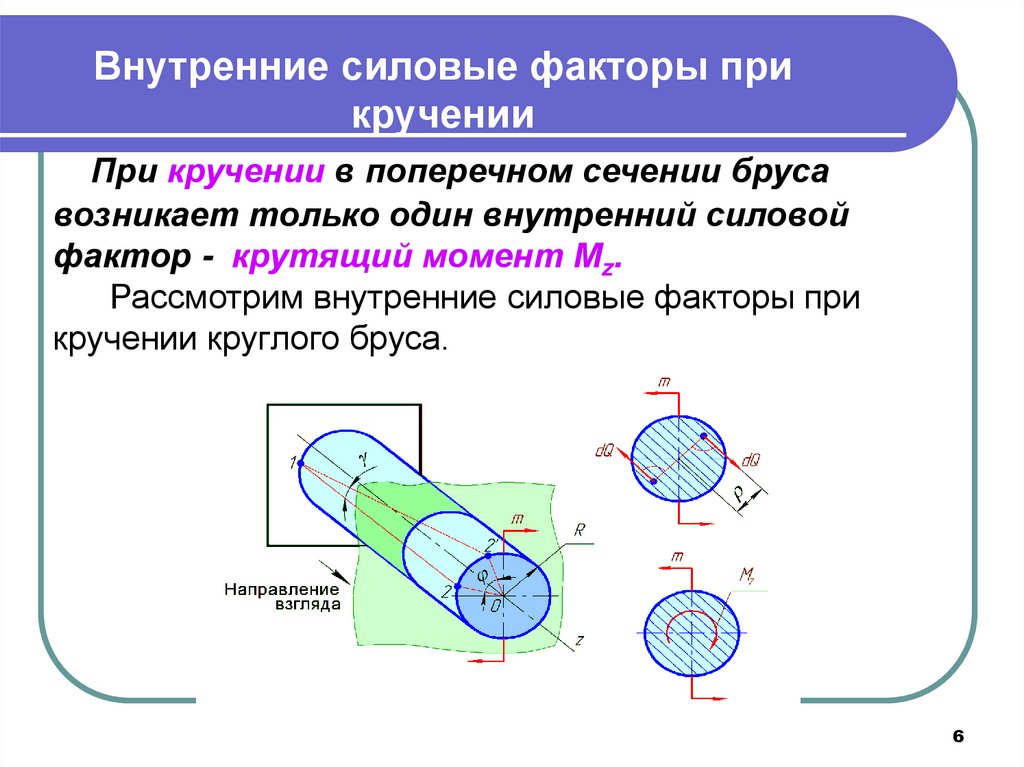
Внутренние силовые факторы при
кручении
При кручении в поперечном сечении бруса
возникает только один внутренний силовой
фактор - крутящий момент Мz.
Рассмотрим внутренние силовые факторы при
кручении круглого бруса.
6

7.

Внутренние силовые факторы при
кручении
В Mz – крутящий момент определяется методом сечений.
Крутящий момент в сечении численно равен
сумме моментов внешних сил, действующих на
отсечённую часть.
Мz = ∑m
ПРАВИЛО ЗНАКОВ
Крутящий момент считаем положительным, если
моменты внешних пар сил направлены по часовой
стрелке и отрицательным – против часовой
стрелки, если смотреть со стороны проведенного
сечения.
7

8.

Эпюры крутящих моментов
Характер изменения крутящего момента
по длине вала наглядно представляют
эпюрой крутящих моментов.
8

9.

Пример 1
Для стального вала круглого поперечного сечения
построить эпюры крутящих моментов по длине вала.
Выбрать рациональное расположение колес на
валу.
m1 = 280 Н·м; m2 = 140 Н·м; m3 = 80 Н·м;
Примечание. Рациональным расположением колес
на валу, считается такое, при котором крутящие
моменты принимают минимальные из возможных
значений.
9

10.

Решение
1.Из условия равновесия вала определяем
уравновешивающий момент.
Σmz = 0; m0 - m1 - m2 - m3 = 0;
m0 = m1 + m2 + m3 = 280 + 140 + 80 = 500 Н·м.
10

11.

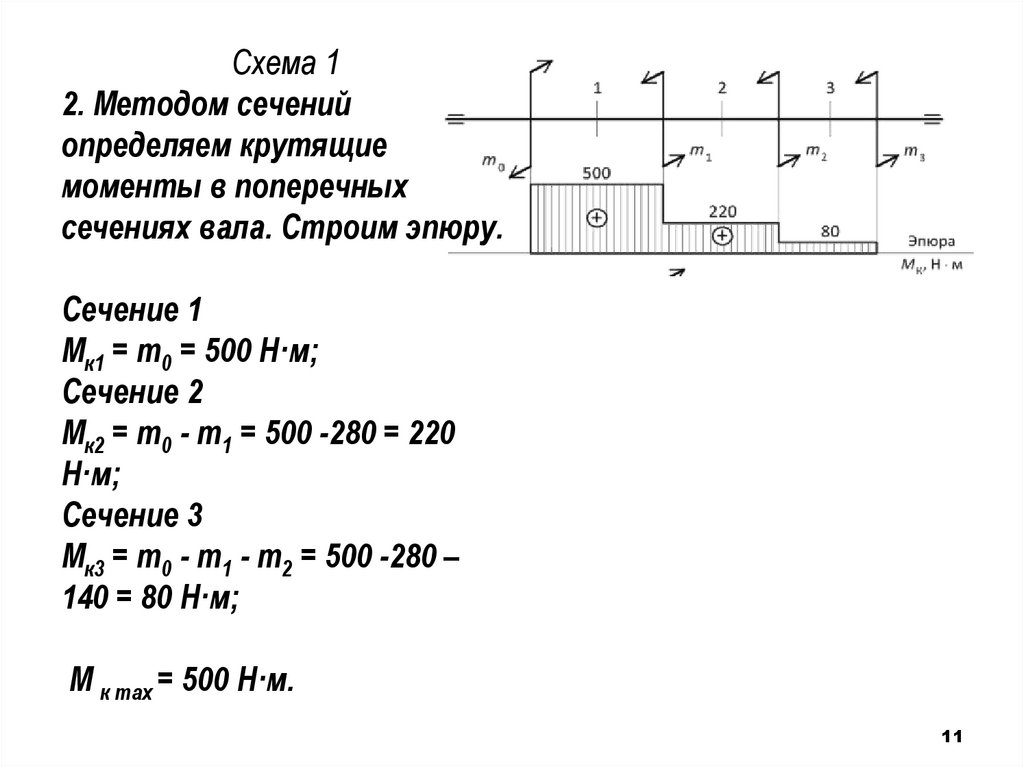
Схема 1
2. Методом сечений
определяем крутящие
моменты в поперечных
сечениях вала. Строим эпюру.
Сечение 1
Мк1 = m0 = 500 Н·м;
Сечение 2
Мк2 = m0 - m1 = 500 -280 = 220
Н·м;
Сечение 3
Мк3 = m0 - m1 - m2 = 500 -280 –
140 = 80 Н·м;
М к max = 500 Н·м.
11

12.

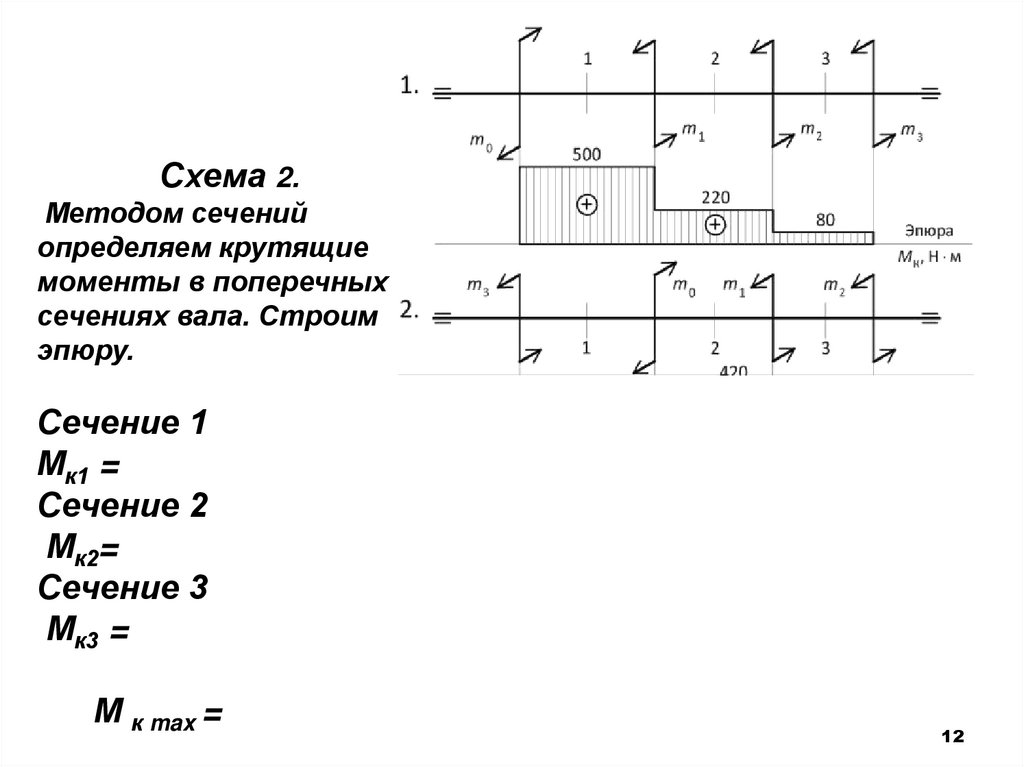
Схема 2.
Методом сечений
определяем крутящие
моменты в поперечных
сечениях вала. Строим
эпюру.
Сечение 1
Мк1 =
Сечение 2
Мк2=
Сечение 3
Мк3 =
М к max =
12

13.

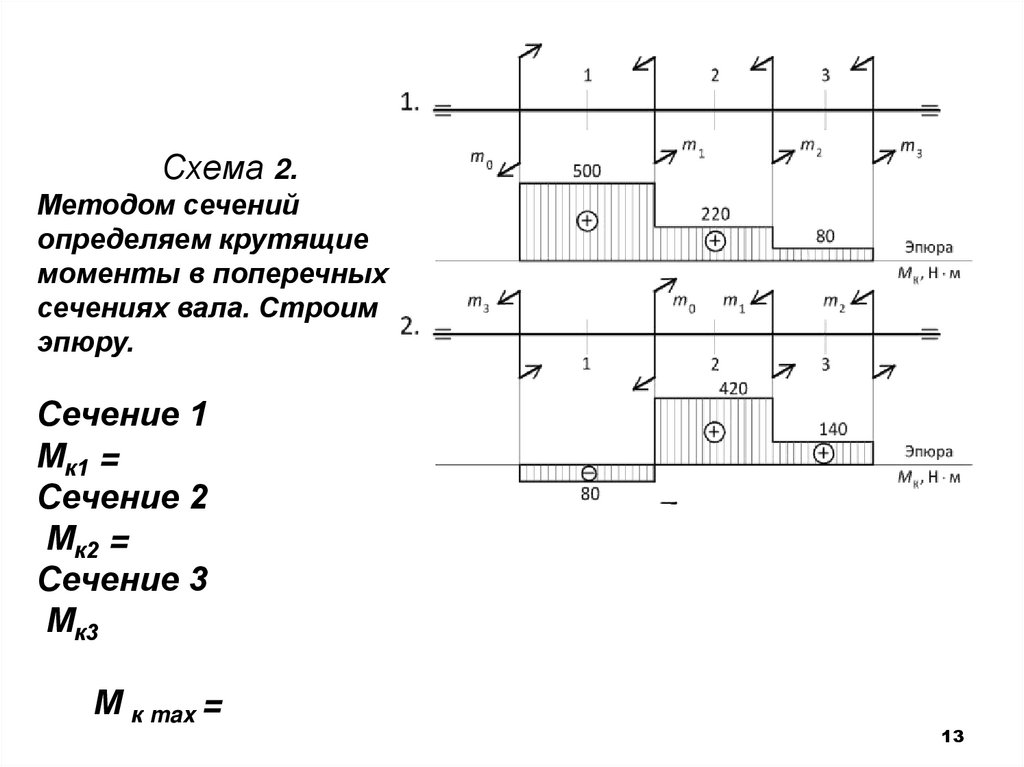
Схема 2.
Методом сечений
определяем крутящие
моменты в поперечных
сечениях вала. Строим
эпюру.
Сечение 1
Мк1 =
Сечение 2
Мк2 =
Сечение 3
Мк3
М к max =
13

14.

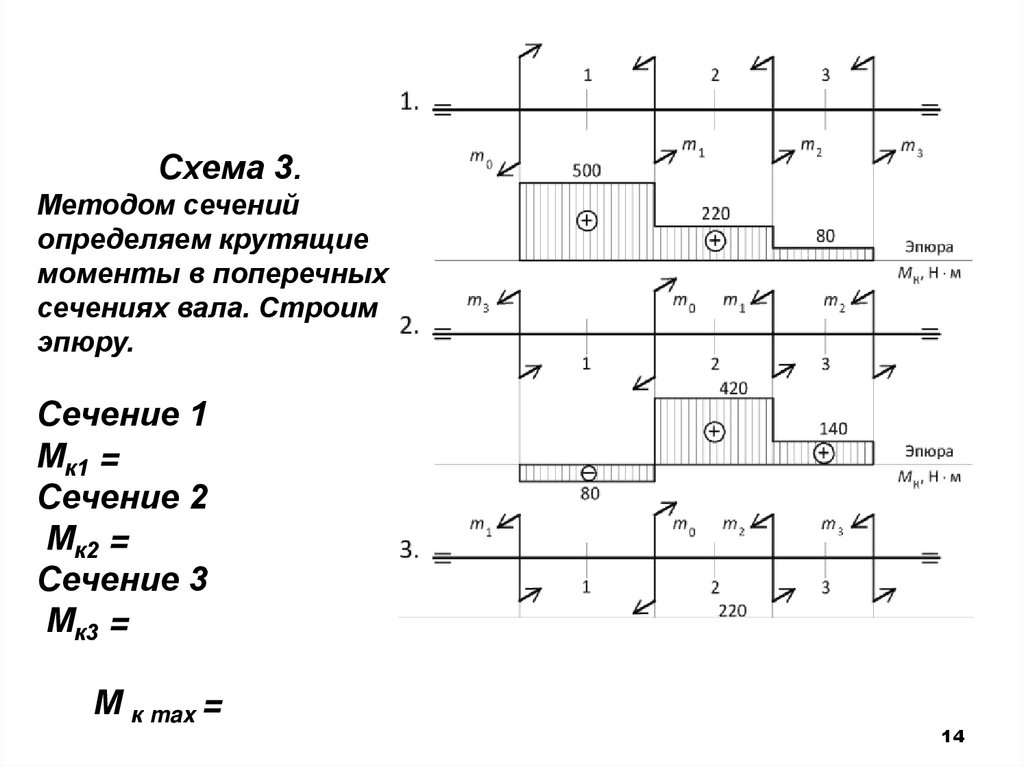
Схема 3.
Методом сечений
определяем крутящие
моменты в поперечных
сечениях вала. Строим
эпюру.
Сечение 1
Мк1 =
Сечение 2
Мк2 =
Сечение 3
Мк3 =
М к max =
14

15.

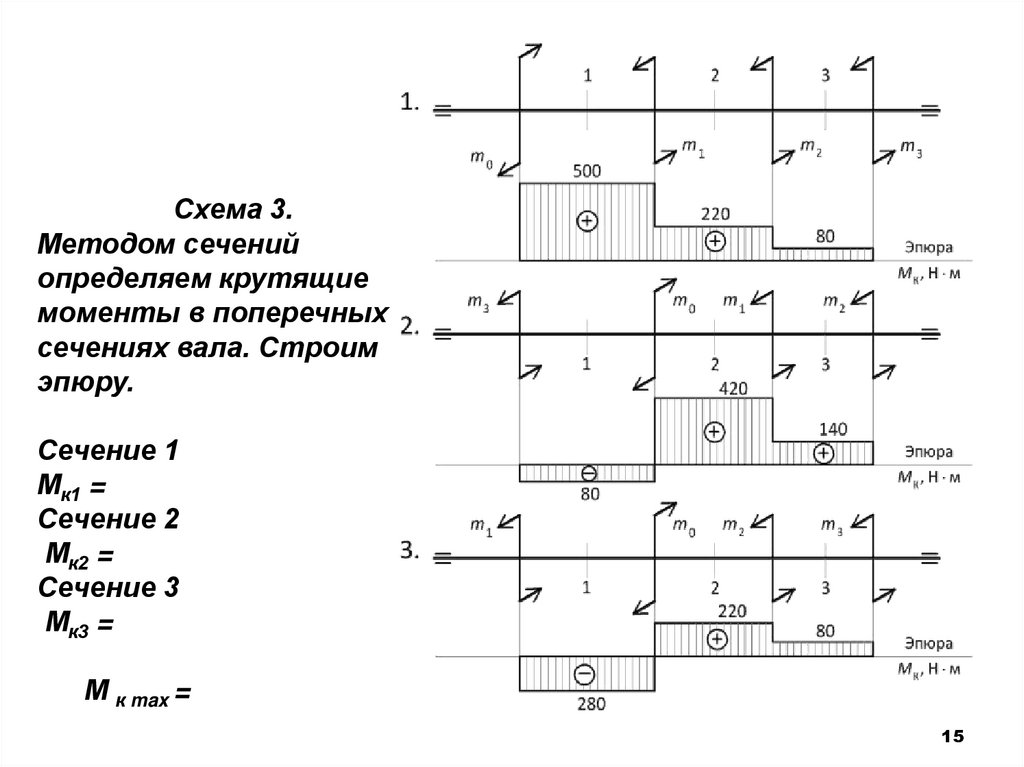
Схема 3.
Методом сечений
определяем крутящие
моменты в поперечных
сечениях вала. Строим
эпюру.
Сечение 1
Мк1 =
Сечение 2
Мк2 =
Сечение 3
Мк3 =
М к max =
15

16.

Тема:
Кручение
ДОМАШНЕЕ ЗАДАНИЕ
автор Олофинская В.П.
ТЕХНИЧЕСКАЯ МЕХАНИКА
Стр.216-222
Ответить на контрольные вопросы
на страницах 221-222
11
16

17.

ЗАНЯТИЕ ОКОНЧЕНО
СПАСИБО
12
17