Решение 23 задачи 16 варианта ОГЭ по математике

1. Решение 23 задачи 16 варианта ОГЭ по математике

Презинтацию подготовила
ученица 9Б класса Юшанова Анна

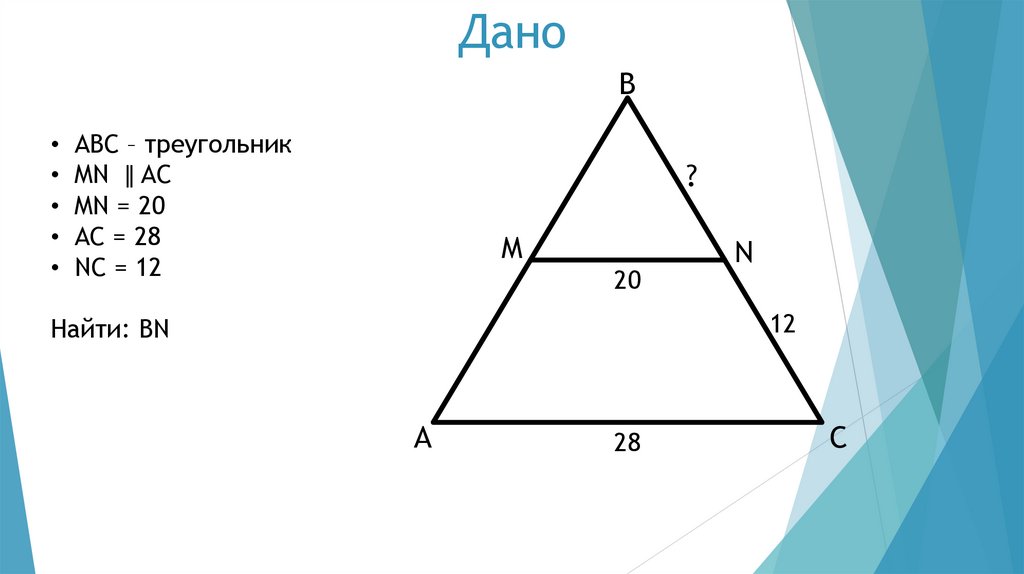
2. Дано

B
• ABC – треугольник
• MN ǁ AC
• MN = 20
• AC = 28
• NC = 12
?
M
20
N
12
Найти: BN
A
28
C

3. Шаг 1. Определения и свойства

Треугольник – фигура, ограниченная тремя отрезками,
соединяющими три точки, не лежащие на одной
прямой (вершины треугольника)
Если прямая параллельна одной из сторон
треугольника и пересекает две другие стороны, то она
образует с ними меньший треугольник, подобный
исходному (теорема о пропорциональных отрезках или
теорема Фалеса)

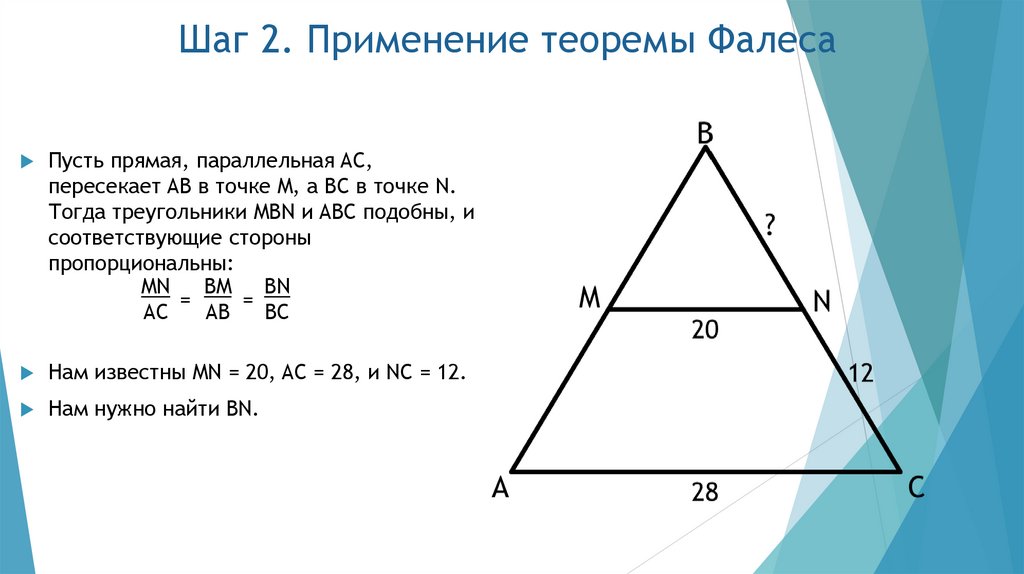
4. Шаг 2. Применение теоремы Фалеса

Пусть прямая, параллельная AC,
пересекает AB в точке M, а BC в точке N.
Тогда треугольники MBN и ABC подобны, и
соответствующие стороны
пропорциональны:
MN
BM
BN
=
=
.
AC
AB
BC
Нам известны MN = 20, AC = 28, и NC = 12.
Нам нужно найти BN.

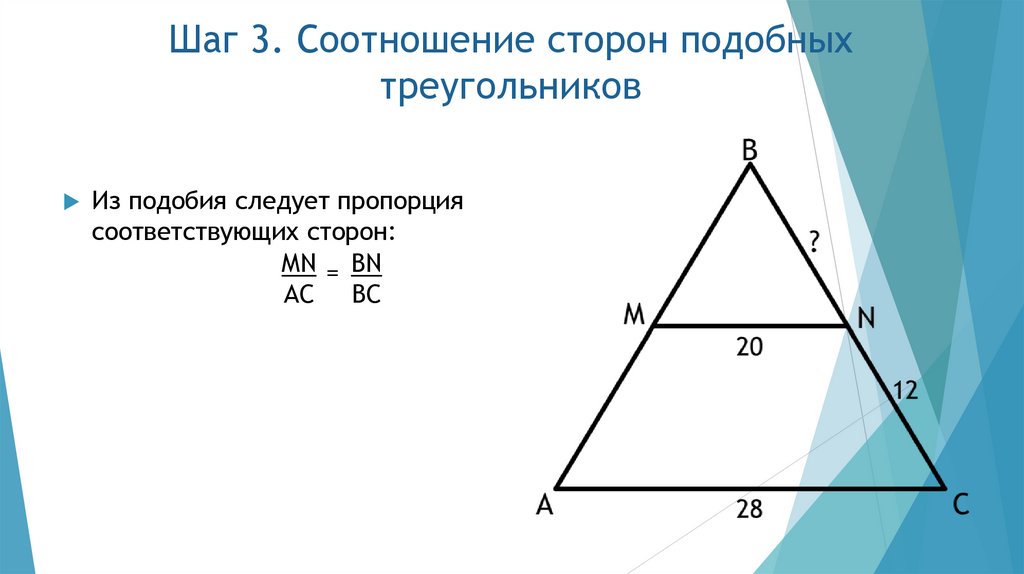
5. Шаг 3. Соотношение сторон подобных треугольников

Из подобия следует пропорция
соответствующих сторон:
MN = BN
AC BC

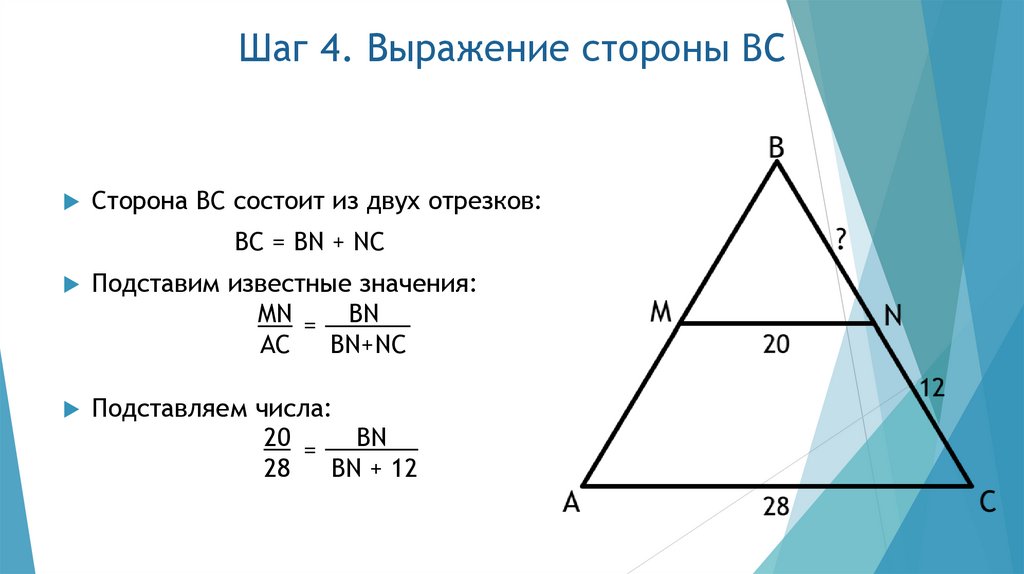
6. Шаг 4. Выражение стороны BC

Сторона BC состоит из двух отрезков:
BC = BN + NC
Подставим известные значения:
MN = BN
AC
BN+NC
Подставляем числа:
20 =
BN
28
BN + 12

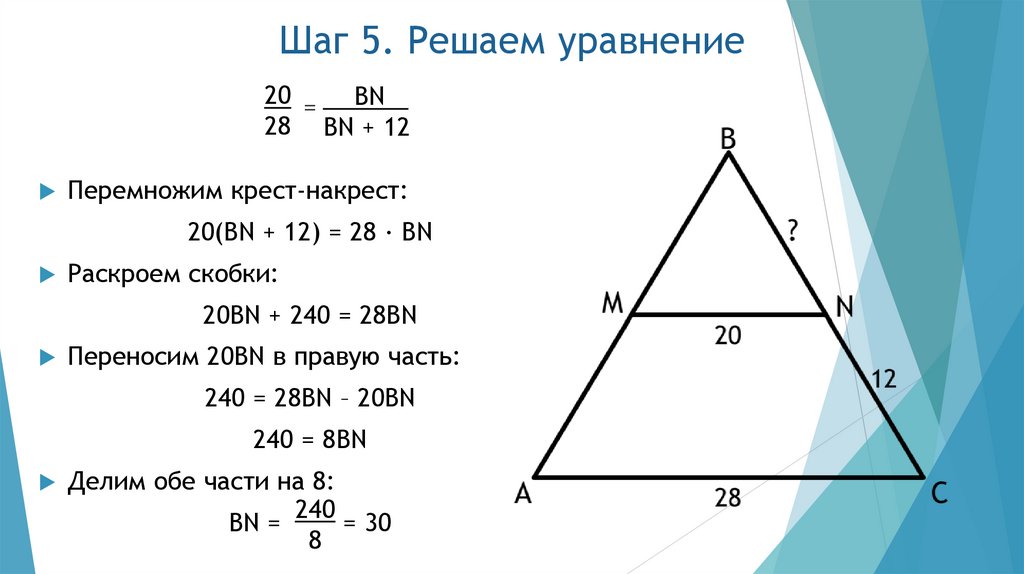
7. Шаг 5. Решаем уравнение

20 = BN
28 BN + 12
Перемножим крест-накрест:
20(BN + 12) = 28 ∙ BN
Раскроем скобки:
20BN + 240 = 28BN
Переносим 20BN в правую часть:
240 = 28BN – 20BN
240 = 8BN
Делим обе части на 8:
BN =
240
= 30
8

8. Ответ

Таким образом, длина отрезка BN равна 30.
Это решение основано на свойстве подобия
треугольников, возникающем при
проведением прямой, параллельной
стороне треугольника, и использовании
пропорций между соответствующими
сторонами.

9. Решение аналогичной задачи

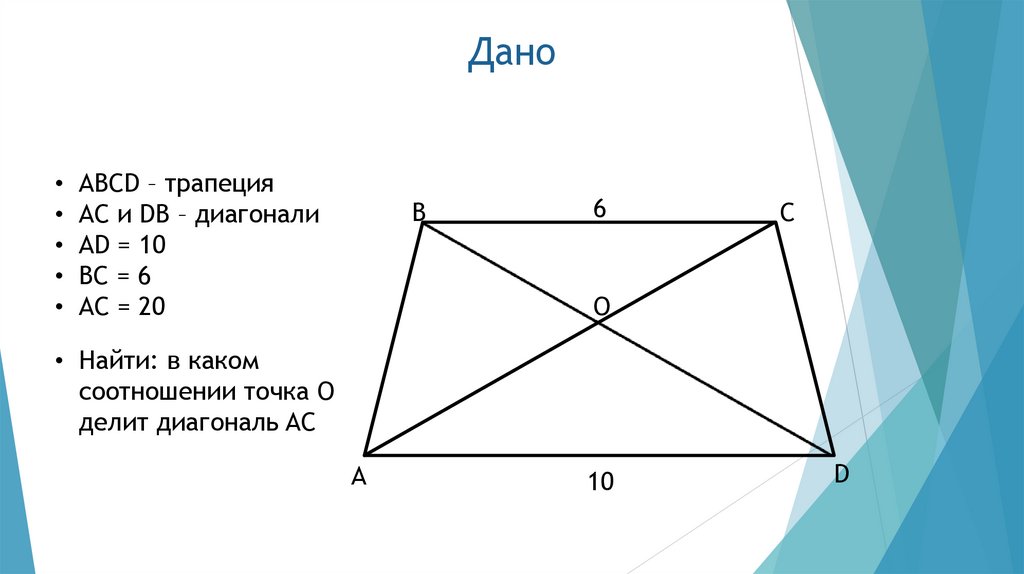
10. Дано

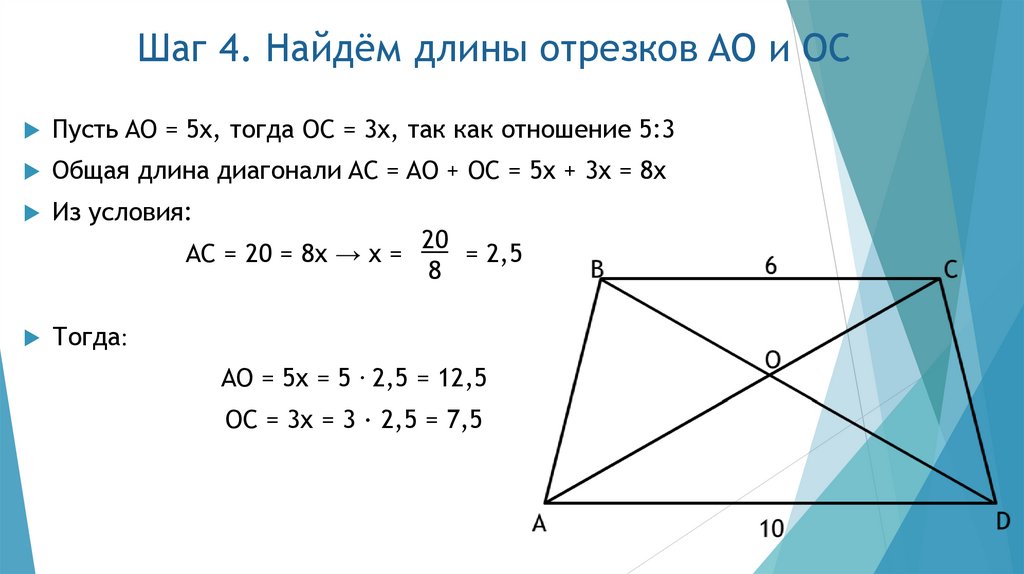
• ABCD – трапеция
• AC и DB – диагонали
• AD = 10
• BC = 6
• AC = 20
B
6
C
O
• Найти: в каком
соотношении точка O
делит диагональ AC
A
10
D

11. Шаг 1. Определения и свойства

Трапеция – четырёхугольник с двумя параллельными
сторонами, называемыми основаниями (BC и AD).
Диагонали трапеции – отрезки, соединяющие
противоположные вершины (AC и BD).
При пересечении диагоналей трапеции точка пересечения O
делит диагонали в отношении, пропорциональном основаниям
трапеции.

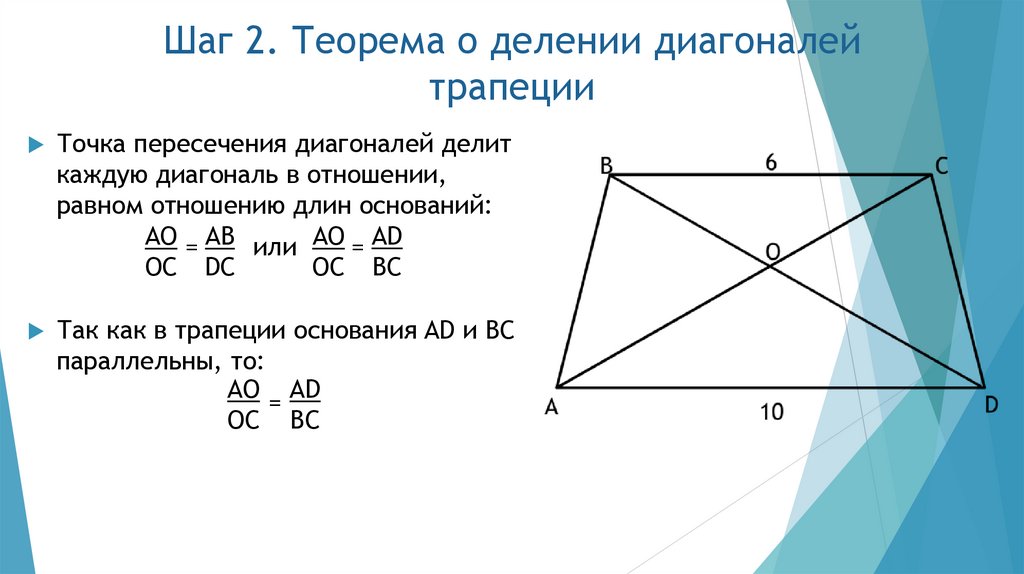
12. Шаг 2. Теорема о делении диагоналей трапеции

Точка пересечения диагоналей делит
каждую диагональ в отношении,
равном отношению длин оснований:
AO = AB или AO = AD
OC DC
OC BC
Так как в трапеции основания AD и BC
параллельны, то:
AO AD
=
OC BC

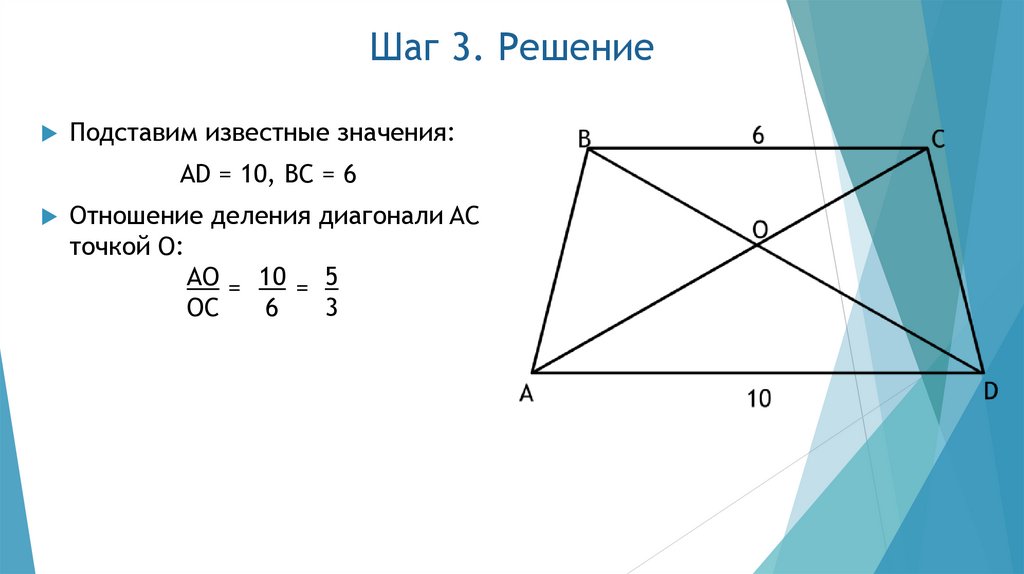
13. Шаг 3. Решение

Подставим известные значения:
AD = 10, BC = 6
Отношение деления диагонали AC
точкой O:
AO = 10 = 5
OC
6
3

14. Шаг 4. Найдём длины отрезков AO и OC

Пусть AO = 5x, тогда OC = 3x, так как отношение 5:3
Общая длина диагонали AC = AO + OC = 5x + 3x = 8x
Из условия:
AC = 20 = 8x → x =
20
= 2,5
8
Тогда:
AO = 5x = 5 ∙ 2,5 = 12,5
OC = 3x = 3 ∙ 2,5 = 7,5

15. Итог

Точка O делит диагональ AC в отношении 5:3, то есть:
AO:OC = 5:3
AO = 12,5
OC = 7,5

16. Объяснение через подобие треугольников

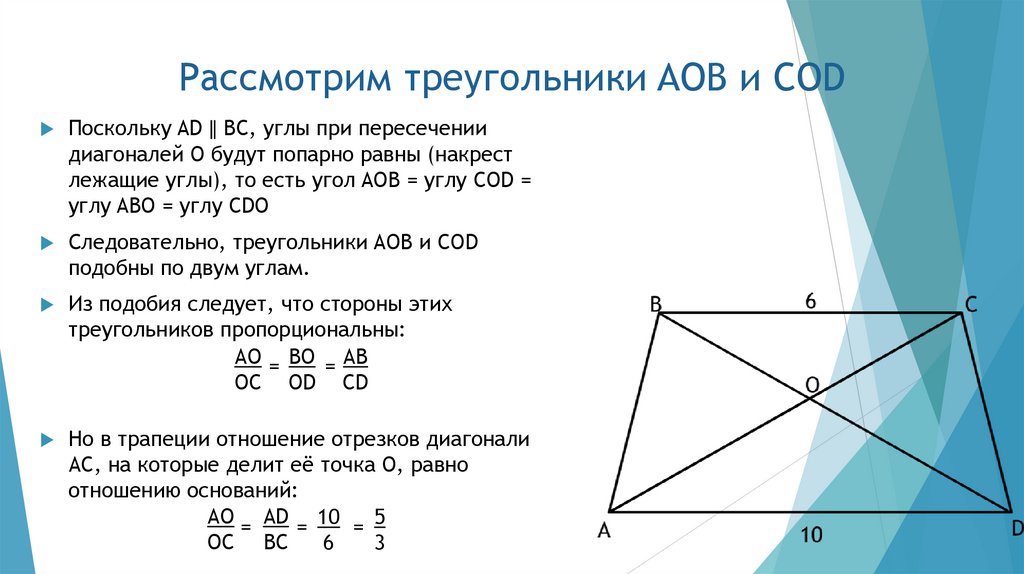
17. Рассмотрим треугольники AOB и COD

Поскольку AD ǁ BC, углы при пересечении
диагоналей O будут попарно равны (накрест
лежащие углы), то есть угол AOB = углу COD =
углу ABO = углу CDO
Следовательно, треугольники AOB и COD
подобны по двум углам.
Из подобия следует, что стороны этих
треугольников пропорциональны:
AO = BO = AB
OC OD CD
Но в трапеции отношение отрезков диагонали
AC, на которые делит её точка O, равно
отношению оснований:
AO = AD = 10 = 5
OC BC
6
3

18. Итог

Точка O делит диагональ AC в отношении 5:3, то есть:
AO:OC = 5:3
Поскольку AC = 20, можно найти длины отрезков:
AO =
5
5
∙ 20 =
∙ 20 = 12,5
5+3
8
OC = 3 ∙ 20 = 7,5
8

19. Ответ

Таким образом, длина AO равна 12,5 и длина OC равна 7,5