Некоторые виды распределения ДСВ, их числовые характеристики

1. Некоторые виды распределения ДСВ, их числовые характеристики

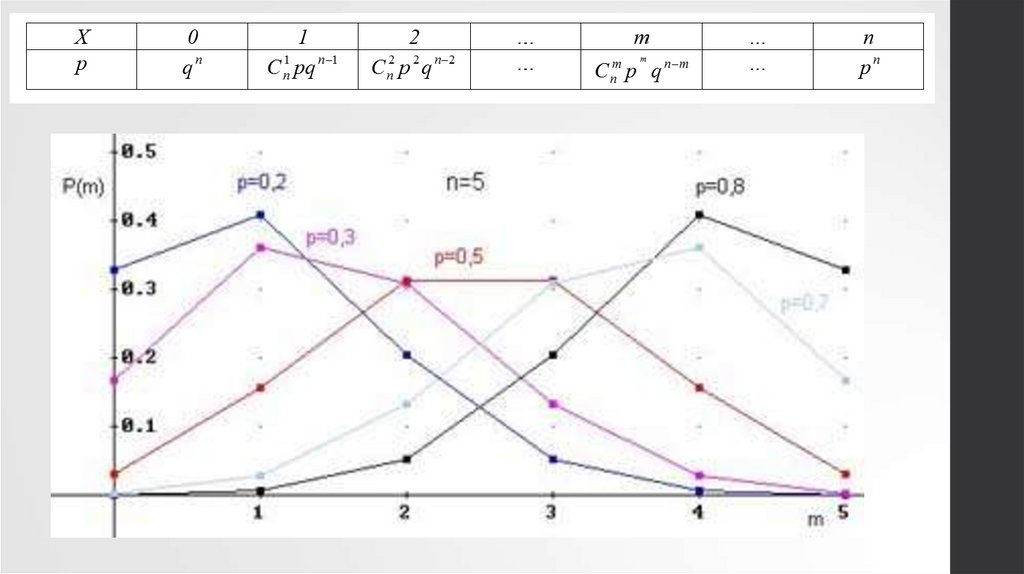
2. 1. Биномиальные распределения

Распределение
вероятностей,
определяемое
формулой
Бернулли,
называется биномиальным законом
распределения ДСВ.

3.

4. 1. Биномиальные распределения

Числовые характеристики биномиального распределения
могут быть вычислены по формулам:
М(Х) = пр
D(X) = npq

5.

Пример 1.
Вероятность попадания в цель при стрельбе из орудия равна
0,65. Найти математическое ожидание и среднеквадратичное
отклонение общего числа попаданий, если произведено 20
выстрелов.

6.

Распределение Пуассона
Пусть производится п независимых испытаний, в которых появление
события А имеет вероятность р, причем число испытаний п достаточно
велико, а вероятность появления события А в каждом испытании мало.
M (X )
D( X )

7.

Примерами случайных величин, имеющих распределение Пуассона, могут быть:
▪число вызовов на телефонной станции за некоторое время
▪число опечаток в большом тексте
▪число бракованных изделий в большой партии и т.д.

8. 2. Гипергеометрические распределения

Эти распределения отличаются от биномиальных тем, что проводятся
зависимые повторные испытания.
В этом случае вероятности вычисляются по определению вероятности с
помощью сочетаний.
Числовые же характеристики
формулам:
таких распределений можно найти по
N – количество элементов в исходном множестве, М – количество
элементов, обладающих нужным свойством, n – число испытаний

9.

m
M
n m
N M
n
N
C C
P ( X m)
C
Гипергеометрическое распределение имеет случайная величина Х,
равная числу объектов, обладающих заданным свойством, среди n
объектов, случайно извлеченных (без возврата) из совокупности N
объектов, М из которых обладают этим свойством.
Например:
•В партии из 10 деталей 3 бракованных. Извлекается 4 детали. Х –
число годных деталей среди извлеченных. (n = 4, N = 10, M = 3)

10.

Пример 2.
В партии, состоящей из 10 МК, семь – стандартных.
Контролер ОТК наудачу проверил два МК. Найти числовые
характеристики СВ Х – «числа обнаруженных стандартных
МК».

11. 3. Геометрические распределения

ДСВ Х имеет геометрическое распределение, если она принимает
значения 1, 2, 3, …. с вероятностями
(т.е. вероятности рк образуют убывающую геометрическую прогрессию с
первым членом р и знаменателем q)
• Примерами таких величин могут быть:
• число выстрелов до первого попадания
• число испытаний прибора до первого отказа
• число бросаний монеты до первого выпадения решки и т.д.
Для таких ДСВ числовые характеристики вычисляются по формулам:

12.

Пример 3.
Баскетболист бросает мяч до первого попадания.
Вероятность попадания равна 0,8. Х – «число бросков», если
имеется пять попыток. Составьте закон распределения ДСВ
Х и найдите все ее числовые характеристики.

13.

14.

Пример 4.
Для данного баскетболиста вероятность попадания мяча в
кольцо равна 0,8. Х – «число попаданий в серии из пяти
бросков». Составьте закон распределения ДСВ Х и найдите
все ее числовые характеристики.
Пример 5.
Среди десяти баскетболистов семеро имеют рост более 2
метров. На площадке играют пять человек. Х – «число
низкорослых баскетболистов на площадке». Составьте закон
распределения ДСВ Х и найдите все ее числовые
характеристики.