Формула пика и её применение

1.

Областное государственное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №3 с углубленным изучением отдельных предметов г. Строитель»
Белгородской области
Индивидуальный итоговый проект
Выполнил: Холод Артем,
учащийся 9 «Б» класса
ОГБОУ «СОШ №3 с УИОП
г Строитель»
Руководитель – Сапенко А.Е.,
учитель математики
ОГБОУ «СОШ №3 г. Строитель»
2024.

2. Задачи на клетчатой бумаге: Вычислить площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см и

записать ответ в квадратных сантиметрах.

3.

Обозначение
задания в
работе
18
Контролируемые элементы
Уметь выполнять действия с
геометрическими фигурами,
координатами и векторами
Процент
выполнения
в 2021 году
Процент
выполнения
в 2022 году
Процент
выполнения
в 2023 году
80,4%
76,3%
69,2%

4.

С подобной задачей каждый выпускник школы
встретится на Государственной Итоговой аттестации,
а так же в повседневной жизни. Поэтому, можно
сделать вывод о необходимости подробного изучения
данной
темы
для
нахождения
наиболее
рационального метода решения задач на вычисления
площади любой фигуры на клетчатой бумаге .

5.

Объект исследования: задачи на клетчатой бумаге
Предмет исследования: задачи на вычисление площади
многоугольника на клетчатой бумаге, методы и приёмы их
решения.
Методы исследования: моделирование, сравнение,
обобщение, аналогии, изучение литературных и Интернетресурсов, анализ и классификация информации.

6.

1.Выяснение существования иной, отличной от
школьной программы, формулы нахождения
площади решетчатого многоугольника.
2.Области применения искомой формулы.

7. Задачи исследования

Подобрать необходимую литературу
Отобрать материал для исследования, выбрать главную,
интересную, понятную информацию
Проанализировать
и
систематизировать
полученную
информацию
Найти различные методы и приёмы решения задач на клетчатой
бумаге
Создать электронную презентацию работы для представления
собранного материала одноклассникам.
Провести практическое занятие с одноклассниками по данной
теме.
• Изготовить справочный буклет для учащихся и выпускников
школ

8.

• Теоретическая значимость исследования: расширение знаний о
способах и наиболее рациональном методе вычисления площадей
многоугольников
• Практическая значимость исследования: обобщение опыта,
издание справочного буклета, который может быть использован при
изучении геометрии, подготовке к проверочным и экзаменационным
работам учащимися.

9.

Способы
вычисления
площади
многоугольника

10.

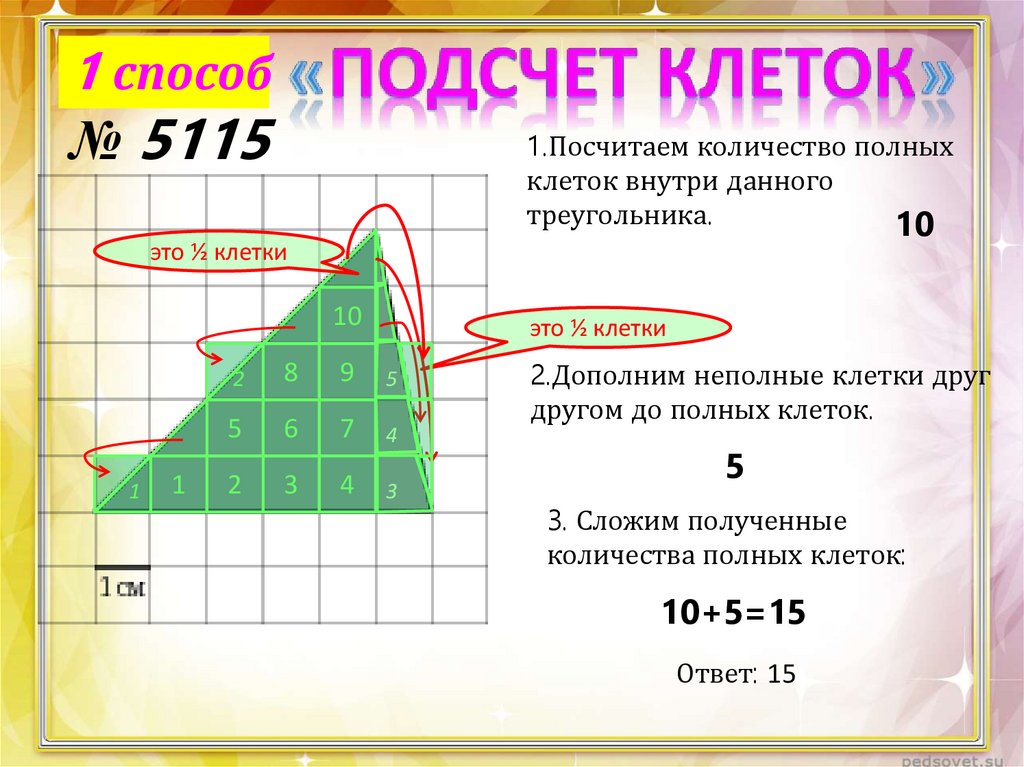
1 способ
№ 5115
1.Посчитаем количество полных
клеток внутри данного
треугольника.
10
это ½ клетки
10
1
1
это ½ клетки
2
8
9
5
5
6
7
4
2
3
4
3
2.Дополним неполные клетки друг
другом до полных клеток.
5
3. Сложим полученные
количества полных клеток:
10+5=15
Ответ: 15

11.

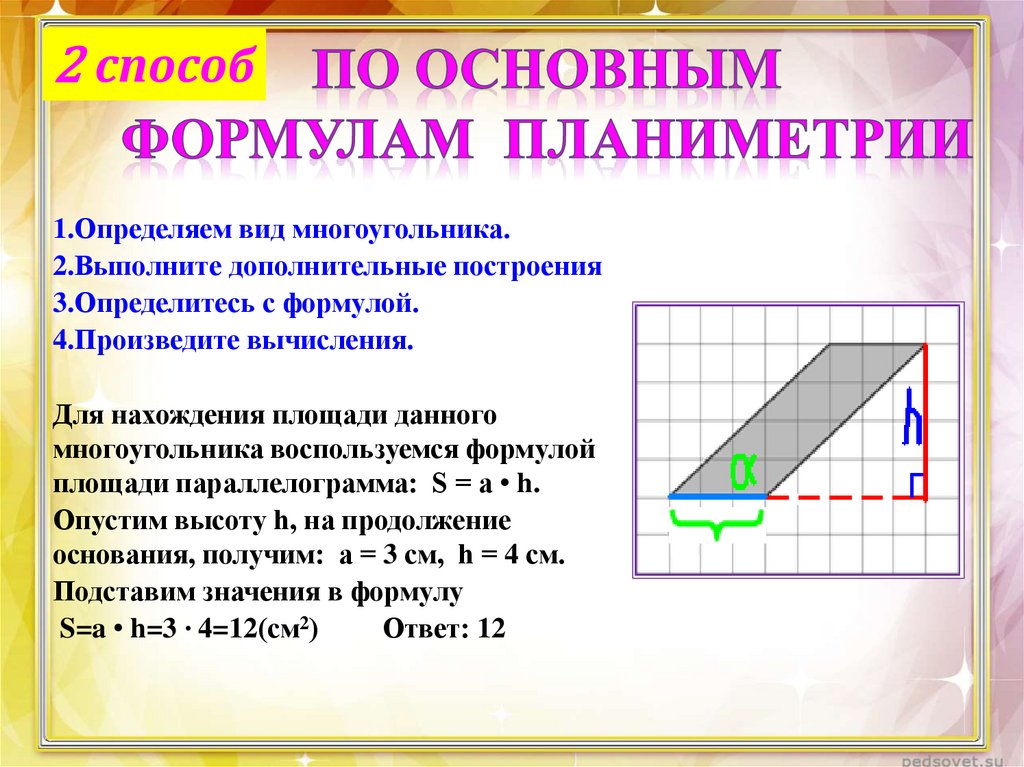
2 способ
1.Определяем вид многоугольника.
2.Выполните дополнительные построения
3.Определитесь с формулой.
4.Произведите вычисления.
Для нахождения площади данного
многоугольника воспользуемся формулой
площади параллелограмма: S = a • h.
Опустим высоту h, на продолжение
основания, получим: а = 3 см, h = 4 см.
Подставим значения в формулу
S=a • h=3 ∙ 4=12(см2)
Ответ: 12

12.

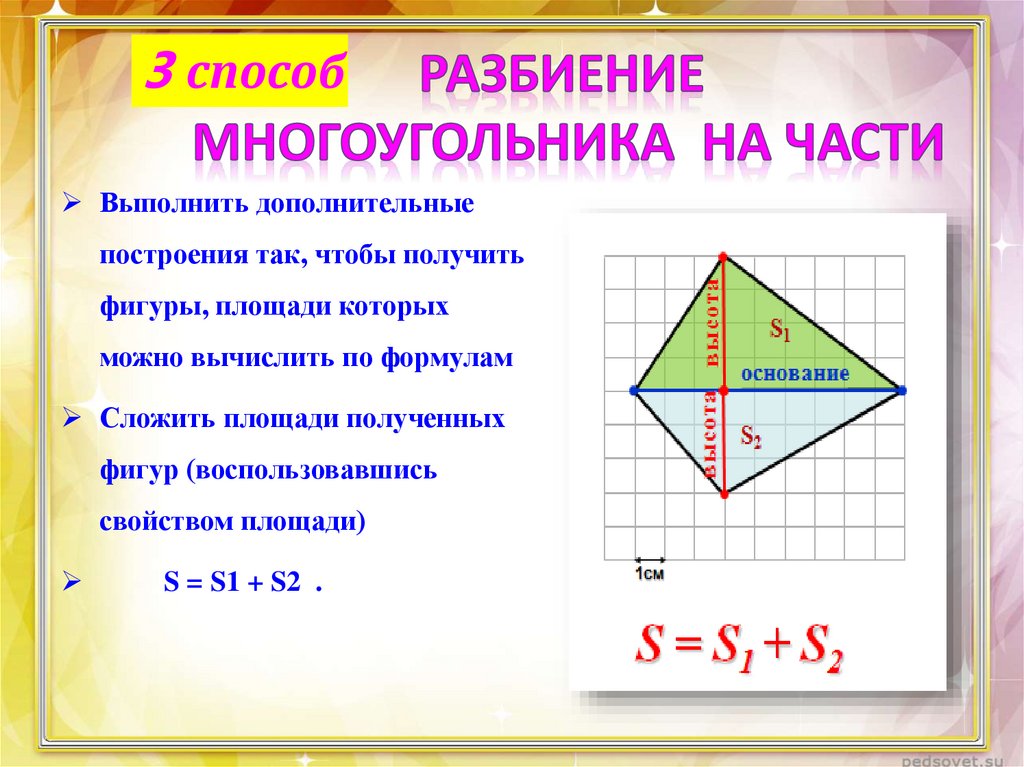
3 способ
Выполнить дополнительные
построения так, чтобы получить
фигуры, площади которых
можно вычислить по формулам
Сложить площади полученных
фигур (воспользовавшись
свойством площади)
S = S1 + S2 .

13.

4 способ
7
S1
S- ?
7
S2
S4
S5
S3
Достроить многоугольник до
прямоугольника
Найти размеры и площадь
полученного прямоугольника
Найти площади достроенных фигур
Вычесть сумму площадей
достроенный фигур (лишних частей)
из площади прямоугольника
1см
• В этом случае площадь
многоугольника можно найти, вписав
его в прямоугольник. Из площади
прямоугольника вычесть площадь
четырех треугольников и квадрата.
S 7 7 (3,5 7 2 2,5 1)
6
3 3
3
10 х
х

14. « Нахождение площади многоугольника с помощью формулы Пика»

5 способ
Рассмотрим многоугольник,
вершины которого
находятся в узлах
целочисленной решётки, т. е.
имеют целочисленные
координаты. Существует
формула, позволявшая
найти его площадь путём
подсчёта числа
содержащихся в нём узлов.
Линии, идущие по сторонам клеток,
образуют клетчатую решётку, а
вершины клеток — узлы этой
решётки)

15. « Нахождение площади многоугольника с помощью формулы Пика»

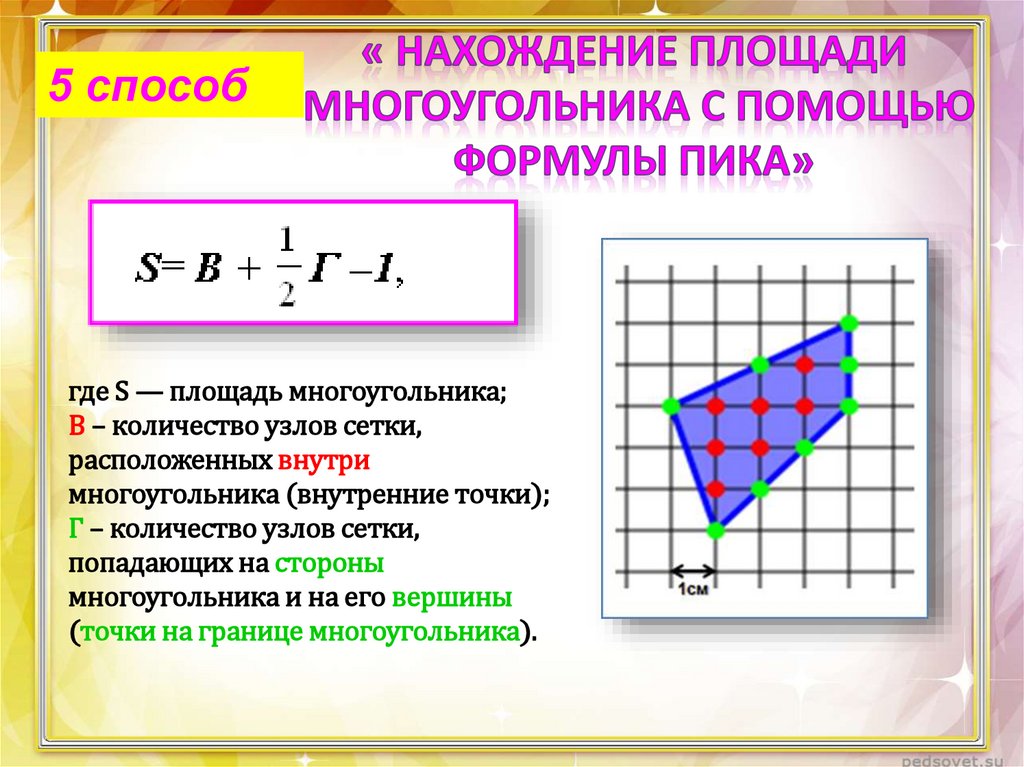
5 способ
где S — площадь многоугольника;
В – количество узлов сетки,
расположенных внутри
многоугольника (внутренние точки);
Г – количество узлов сетки,
попадающих на стороны
многоугольника и на его вершины
(точки на границе многоугольника).

16. « Нахождение площади многоугольника с помощью формулы Пика»

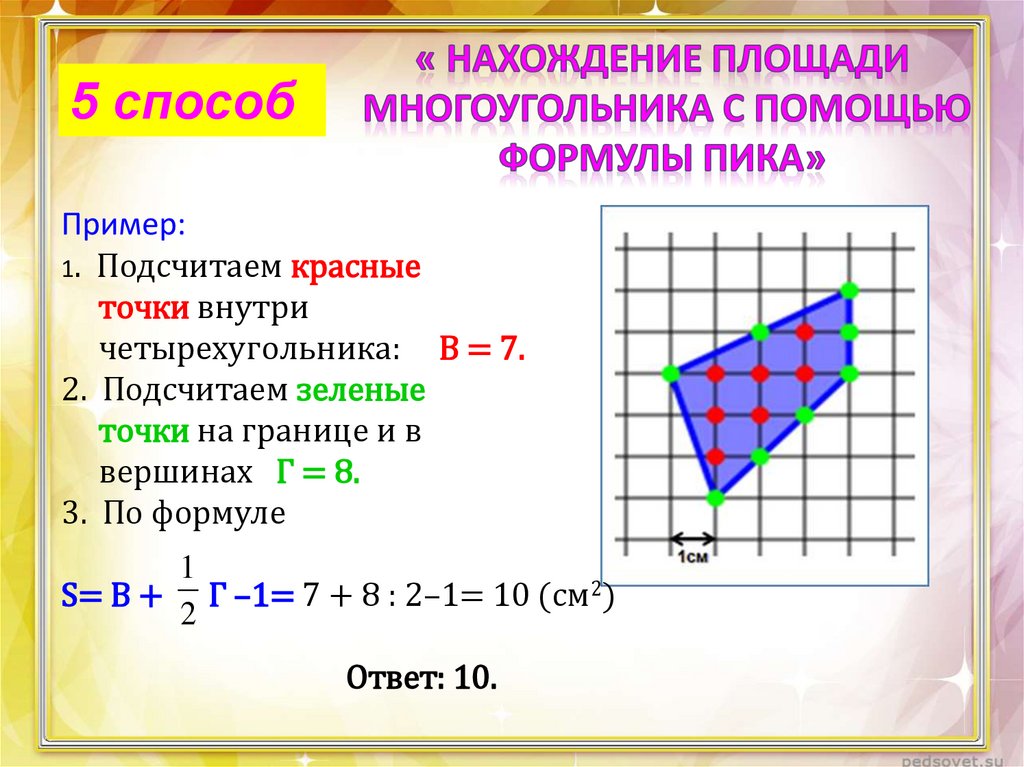
5 способ
Пример:
1. Подсчитаем красные
точки внутри
четырехугольника: В = 7.
2. Подсчитаем зеленые
точки на границе и в
вершинах Г = 8.
3. По формуле
1
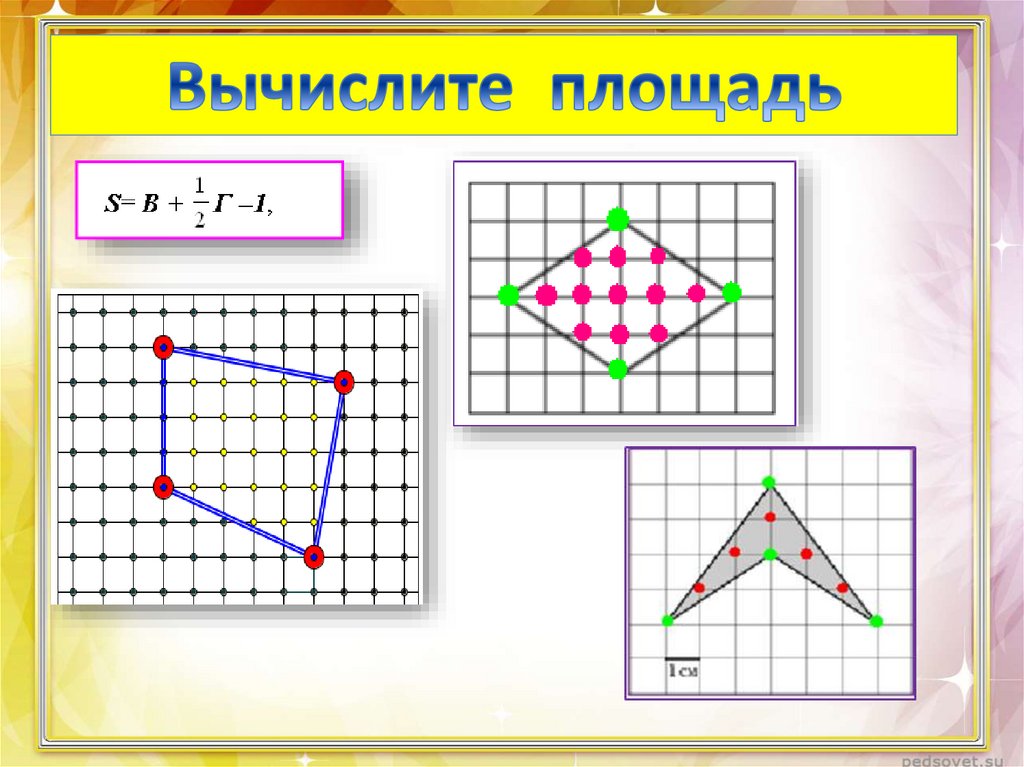
S= В + Г –1= 7 + 8 : 2–1= 10 (см2)
2
Ответ: 10.

17.

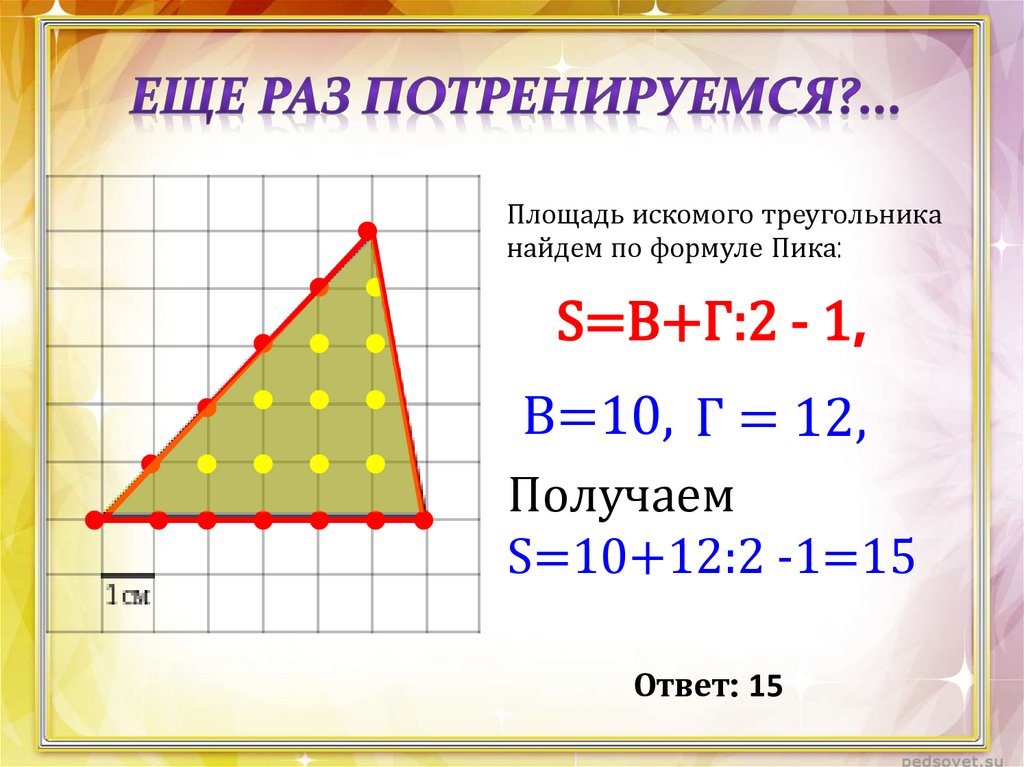
Площадь искомого треугольника
найдем по формуле Пика:
S=В+Г:2 - 1,
В=10, Г = 12,
Получаем
S=10+12:2 -1=15
Ответ: 15

18.

19.

20.

21.

Задача № 4. Прототип задания 4 (№ 27552)
Найдите
площадь
прямоугольника,
изображенного на клетчатой бумаге с размером
клетки 1 см х 1 см
(см. рис.). Ответ дайте в
квадратных сантиметрах.
Решение:
1 способ.
Воспользуемся методом «Разбиения
многоугольника на части». Получим два равных треугольника. (Основание
общее – диагональ, катеты – противолежащие стороны прямоугольника,
также равны. Значит, треугольники равны по трем сторонам.)
Воспользуемся
формулой
площади треугольника.
Опустим высоту h = 2 см, основание а = 5 см.
S = 1 a · h = 1 ∙ 5 · 2 = 5 (см2).
2
2
Значит, площадь прямоугольника равна
SABCD = 2S = 2 ∙ 5 = 10 (см2).
2 способ. По формуле Пика
S=В+
1
Г – 1 = 9 + 4 : 2 – 1 = 10 (см2).
2
Ответ: 10
Вывод: По моему по Формуле Пика эту задачу решать
проще, но проверить решение задачи удобно , используя
формулы и свойстсва площадей.

22.

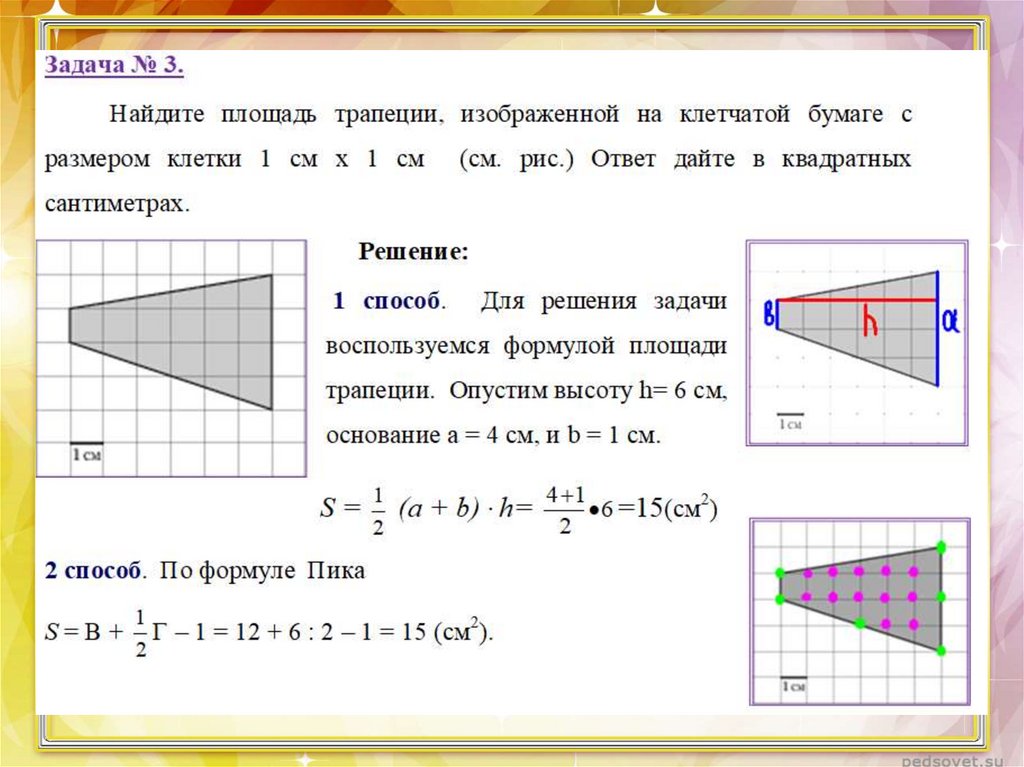
Задача № 5.
Прототип задания 4 (№ 27554)
Найдите площадь четырехгольника, изображенного
на клетчатой бумаге с размером клетки 1 см х 1см
(см. рис.). Ответ дайте в квадратных сантиметрах
Решение:
Если
данную
задачу
решать
«Методом
достраивания до прямоугольника, то необходимо
будет найти площадь самого прямоугольника, затем площади четырех
разных пряоугольников и найти разность. Данное решение нерационально,
посколку необходимо выполнить 6 – 7 действий, как
минимум.
1 способ.
Воспользуемся методом «Разбиения
многоугольника на части». Получим два треугольника.
S1= 1 a · h1 = 1 ∙ 5 · 2 = 5 (см2).
2
2
S2= 1 a · h2 = 1 ∙ 5 · 3 = 7,5 (см2).
2
2
Найдем сумму площадей данных треугольников.
S = S1 + S2 = 5 + 7,5 = 12,5 (см2),
2 способ. По формуле Пика
S=В+
1
Г – 1 = 10 + 7 : 2 – 1 = 12,5 (см2).
2
Ответ: 12,5
Вывод: По моему по Формуле Пика и эту задачу решать проще.

23.

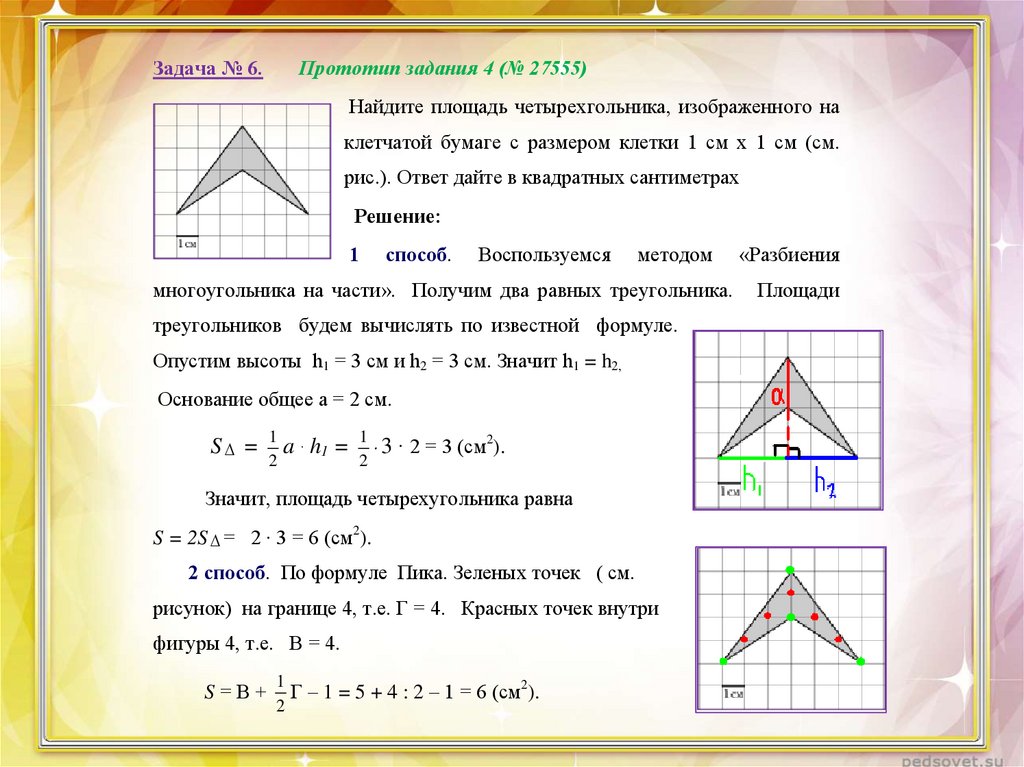
Задача № 6.
Прототип задания 4 (№ 27555)
Найдите площадь четырехгольника, изображенного на
клетчатой бумаге с размером клетки 1 см х 1 см (см.
рис.). Ответ дайте в квадратных сантиметрах
Решение:
1
способ.
Воспользуемся
методом
многоугольника на части». Получим два равных треугольника.
треугольников будем вычислять по известной формуле.
Опустим высоты h1 = 3 см и h2 = 3 см. Значит h1 = h2,
Основание общее а = 2 см.
S = 1 a · h1 = 1 ∙ 3 · 2 = 3 (см2).
2
2
Значит, площадь четырехугольника равна
S = 2S = 2 ∙ 3 = 6 (см2).
2 способ. По формуле Пика. Зеленых точек ( см.
рисунок) на границе 4, т.е. Г = 4. Красных точек внутри
фигуры 4, т.е. В = 4.
S=В+
1
Г – 1 = 5 + 4 : 2 – 1 = 6 (см2).
2
«Разбиения
Площади

24.

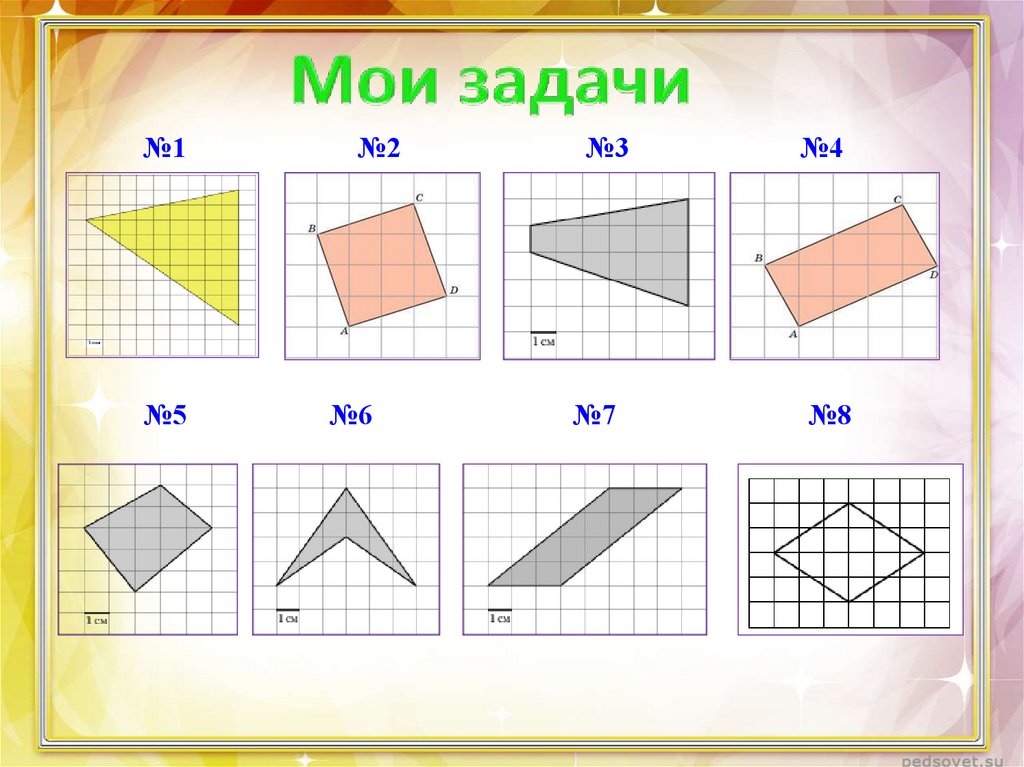
№1
№5
№2
№6
№3
№4
№7
№8

25. Практическое применение формулы ПИКА

ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ
ФОРМУЛЫ ПИКА
Задача 1. Найдите площадь лесного массива (в м²), изображённого на плане
с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м
(рис. 10)
Решение. Найдём S 1 площадь четырёхугольника,
изображённого на клетчатой бумаге по формуле
Пика: S = В +
Рис. 10
1 см² - 200² м²;
В = 8, Г = 7.
Г
-1
2
S 1 = 8 + 7/2 – 1 = 10,5 (см²)
S = 40000 · 10,5 = 420 000 (м²)
Ответ: 420 000 м²

26.

Задача 2. Найдите площадь поля (в м²), изображённого на плане с
квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м. (рис. 11)
Решение. Найдём S 1 площадь четырёхугольника,
изображённого на клетчатой бумаге по формуле Пика: S
=В+
Рис. 11
Ответ: 320 000 м²
Г
-1
2
В = 7, Г = 4.
S 1 = 7 + 4/2 – 1 = 8 (см²)
1 см² - 200² м²;
S = 40000 · 8 = 320 000 (м²)

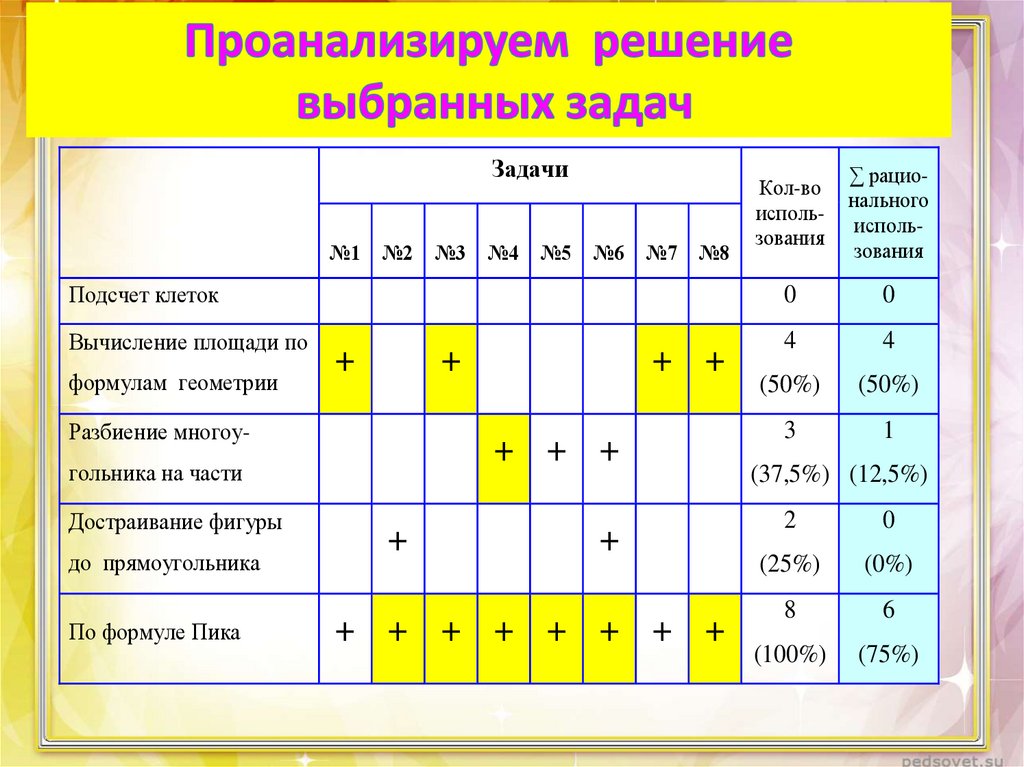
27. Проанализируем решение выбранных задач

Задачи
Кол-во
использования
∑ рационального
использования
Подсчет клеток
0
0
Вычисление площади по
4
4
(50%)
(50%)
3
1
№1 №2 №3 №4 №5 №6 №7 №8
формулам геометрии
+
+
Разбиение многоу-
+ + +
гольника на части
Достраивание фигуры
до прямоугольника
По формуле Пика
+ +
+
+
+ + + + + + + +
(37,5%) (12,5%)
2
0
(25%)
(0%)
8
6
(100%)
(75%)

28. Проанализируем решение выбранных задач

• ВЫВОД: вычисление площади
решетчатого многоугольника по формуле
Пика – это самый рациональный,
универсальный способ.

29. Заключение

• Изучая различные способы решения задач
на нахождение площадей, я убедился, что
существует ещё один, метод вычисления
площадей многоугольников
• по Формуле Пика , он не входит в школьную
программу, но ОЧЕНЬ прост и КРАСИВ!
• Я считаю настоящей жемчужиной своего
исследования формулу Пика, для
вычисления площади многоугольника с
целочисленными вершинами.

30. Заключение

• При помощи формулы Пика большинство
представленных экзаменационных задач
решаются за минуту. Поэтому я всем
рекомендую данный способ запомнить.
• Вывод: каждый из рассмотренных способов в
различных ситуациях представляет собой
рациональный подход и значит, их всех надо знать и
уметь применять.
• Я советую выпускникам решать эти задачи на ОГЭ
двумя-тремя способами (если позволит время) в целях
самопроверки и получения верного результата.

31.

32.

Буклет