Similar presentations:
Точки перегиба функции, выпуклость графика функции. Исследование функции на выпуклость
1. Точки перегиба функции, выпуклость графика функции. Исследование функции на выпуклость
2. Цели обучения:
10.4.1.31 знать определение точки перегиба графика функции инеобходимое и достаточное условие выпуклости вверх (вниз) графика
функции на интервале;
10.4.1.32 уметь находить интервалы выпуклости вверх (вниз) графика
функции
3.
y/
f
(x)=0
/
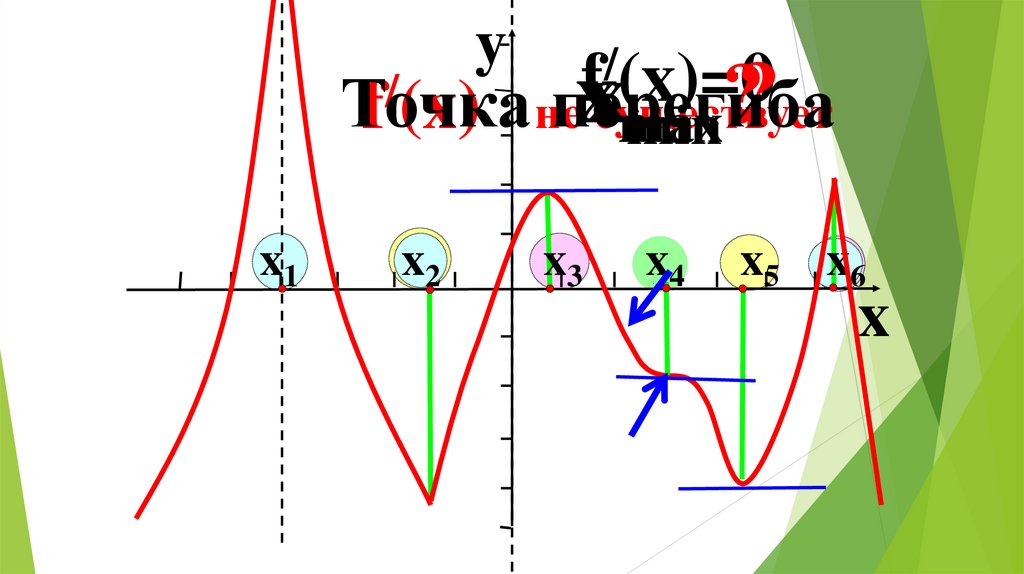
Точка
f (x) неперегиба
существует
max
min
x1
x2
x
x3
??
x4
x5 x6
x
4.
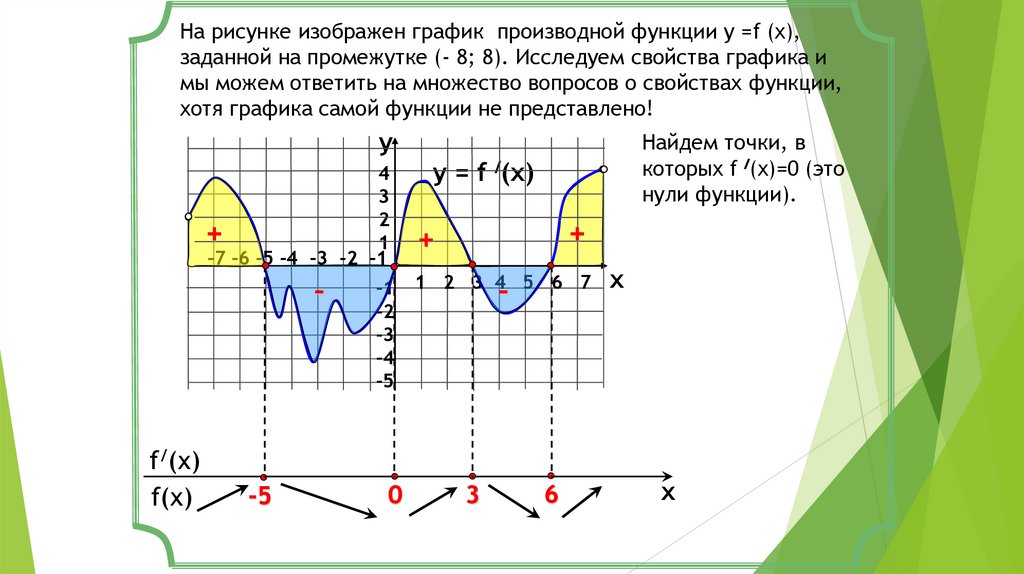
На рисунке изображен график производной функции у =f (x),заданной на промежутке (- 8; 8). Исследуем свойства графика и
мы можем ответить на множество вопросов о свойствах функции,
хотя графика самой функции не представлено!
y
4
3
2
+
1
-7 -6 -5 -4 -3 -2 -1
–
f/(x)
f(x)
-5
-1
-2
-3
-4
-5
0
Найдем точки, в
которых f /(x)=0 (это
нули функции).
y = f /(x)
+
+
1 2 3 4 5 6 7
–
3
6
x
x
5.
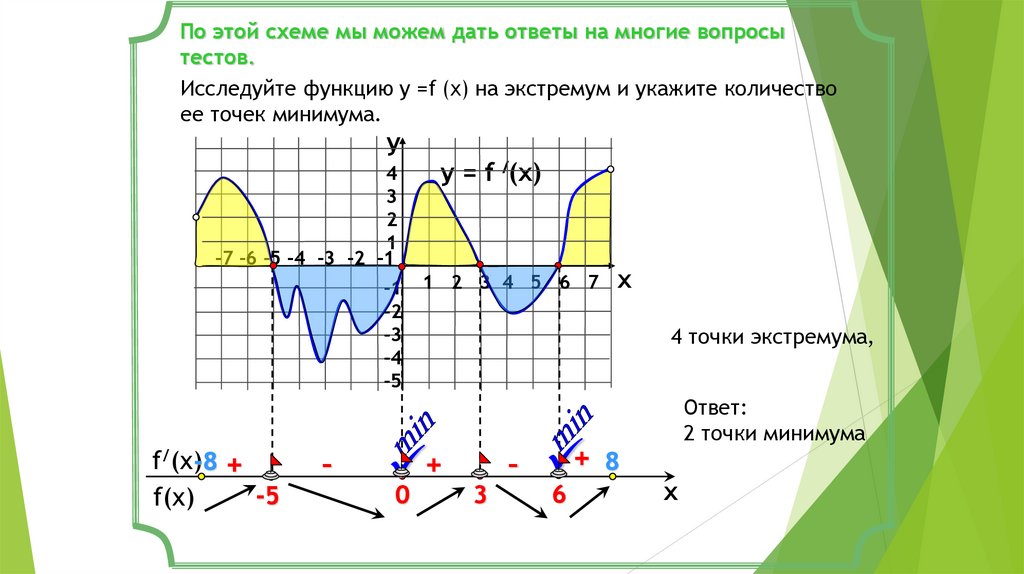
По этой схеме мы можем дать ответы на многие вопросытестов.
Исследуйте функцию у =f (x) на экстремум и укажите количество
ее точек минимума.
y
y = f /(x)
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
f/(x)-8 +
-5
f(x)
–
1 2 3 4 5 6 7
x
4 точки экстремума,
0
+
3
–
+ 8
6
Ответ:
2 точки минимума
x
6.
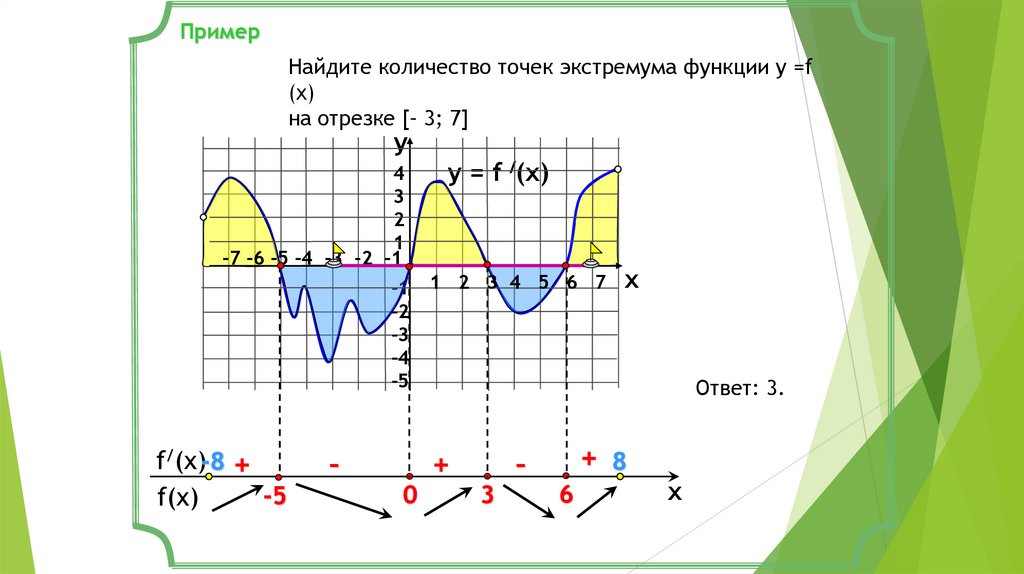
ПримерНайдите количество точек экстремума функции у =f
(x)
на отрезке [– 3; 7]
y
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
f/(x)-8 +
-5
f(x)
–
0
y = f /(x)
1 2 3 4 5 6 7
x
Ответ: 3.
+
3
–
+ 8
6
x
7.
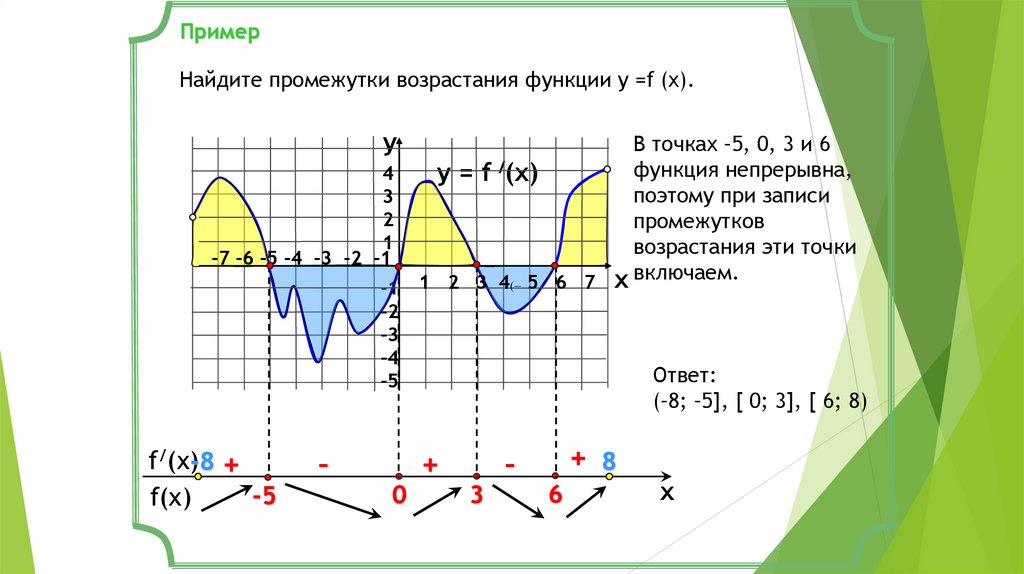
ПримерНайдите промежутки возрастания функции у =f (x).
y
В точках –5, 0, 3 и 6
функция непрерывна,
4
y = f /(x)
поэтому при записи
3
2
промежутков
1
возрастания эти точки
-7 -6 -5 -4 -3 -2 -1
включаем.
x
1
2
3
4
5
6
7
(
-1
-2
-3
-4
-5
f/(x)-8 +
-5
f(x)
–
0
Ответ:
(–8; –5], [ 0; 3], [ 6; 8)
+
3
–
+ 8
6
x
8.
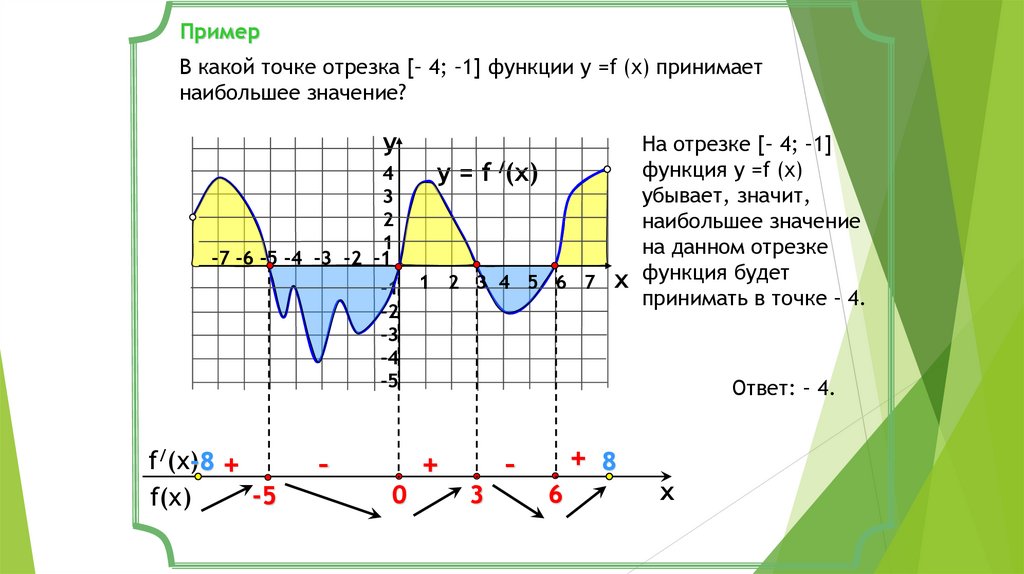
ПримерВ какой точке отрезка [– 4; –1] функции у =f (x) принимает
наибольшее значение?
y
На отрезке [– 4; –1]
функция у =f (x)
4
y = f /(x)
убывает, значит,
3
2
наибольшее значение
1
на данном отрезке
-7 -6 -5 -4 -3 -2 -1
функция будет
x
1
2
3
4
5
6
7
-1
принимать в точке – 4.
-2
-3
-4
-5
f/(x)-8 +
-5
f(x)
–
0
Ответ: – 4.
+
3
–
+ 8
6
x
9.
На рисунке изображен график производной функцииу =f /(x), заданной на промежутке (- 5; 5). Исследуйте
функцию у =f (x) на монотонность и укажите число ее
промежутков убывания.
y
/(x)
y
=
f
4
Не верно!
3
1 3
2
2
3 1
2
1
Не верно!
Верно!
Не верно!
4 4
Проверка (2)
-7 -6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
f/(x)
f(x)
x
1 2 3 4 5 6 7
–
+
1
+
4



 mathematics
mathematics








