Исследование выпуклости графика функции. Точки перегиба

1.

Исследование выпуклости
графика функции. Точки
перегиба
Состав команды:
Переверзев Иван
Катышевский Артем
Шамаров Илья
Киньябулатова Уралия
Ашрафулин Рамиль

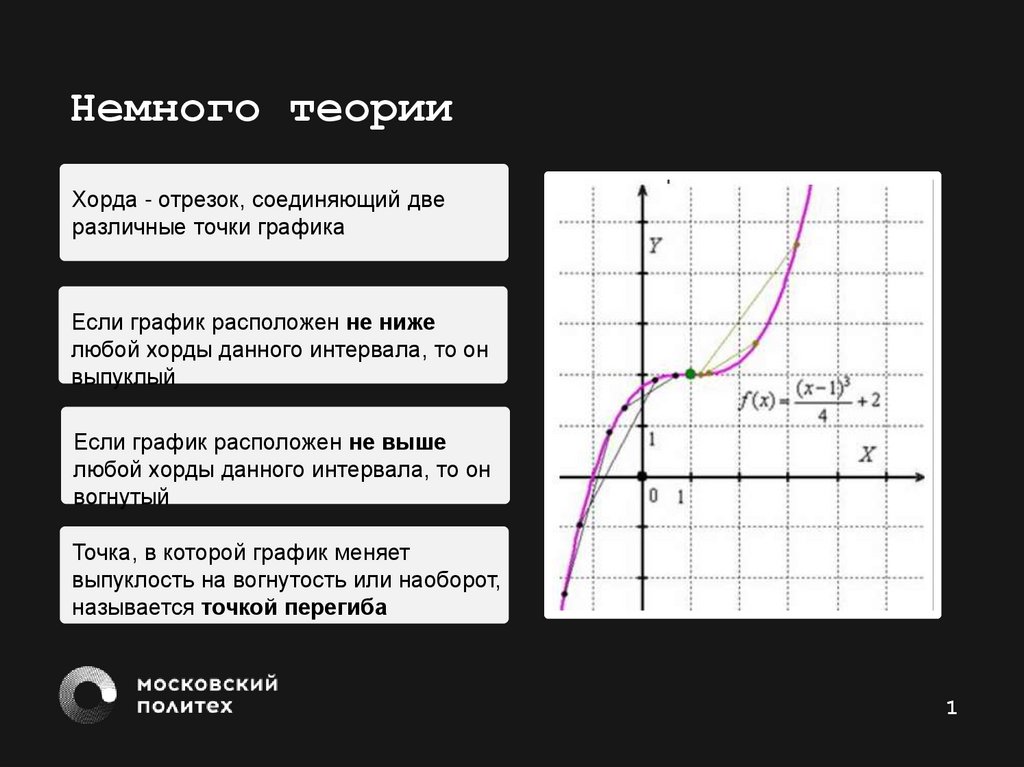
Немного теории
Хорда - отрезок, соединяющий две
различные точки графика
Если график расположен не ниже
любой хорды данного интервала, то он
выпуклый
Если график расположен не выше
любой хорды данного интервала, то он
вогнутый
Точка, в которой график меняет
выпуклость на вогнутость или наоборот,
называется точкой перегиба
1

3.

Как найти?
Если вторая производная f’’(x) < 0 на интервале, то график
функции f(x) является выпуклым на данном интервале
Если вторая производная f’’(x) > 0 на интервале, то график
функции f(x) является вогнутым на данном интервале
Если в точке х0 есть перегиб графика функции y=f(x), то: f’’(x0) = 0
или f’’(x0) не существует
Если вторая производная y = f’’(x) при переходе через точку x0
меняет знак, то в данной точке существует перегиб графика
функции y = f(x)
2

4.

Наш алгоритм
Находим область определения
функции и точки разрыва
Разыскиваем критические значения
(решаем уравнение f’’(x) = 0)
Отмечаем на числовой прямой
найденные точки разрыва и
критические точки, определяем
знаки
Делаем выводы
и даем ответ
3

5.

6.

7.

8.

Наш алгоритм
Находим область определения
функции и точки разрыва
График функции является выпуклым
на интервале (-∞; 1) и вогнут на (1;
+∞). В точке (1; 2) существует точка
перегиба графика
Разыскиваем критические значения
(решаем уравнение f’’(x) = 0)
Отмечаем на числовой прямой
найденные точки разрыва и
критические точки, определяем
знаки
Делаем выводы
и даем ответ
3

Исследование выпуклости графика функции. Точки перегиба

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.