Similar presentations:
Выпуклость функции. Точки перегиба
1.
Выпуклость функции.Точки перегиба.
2.
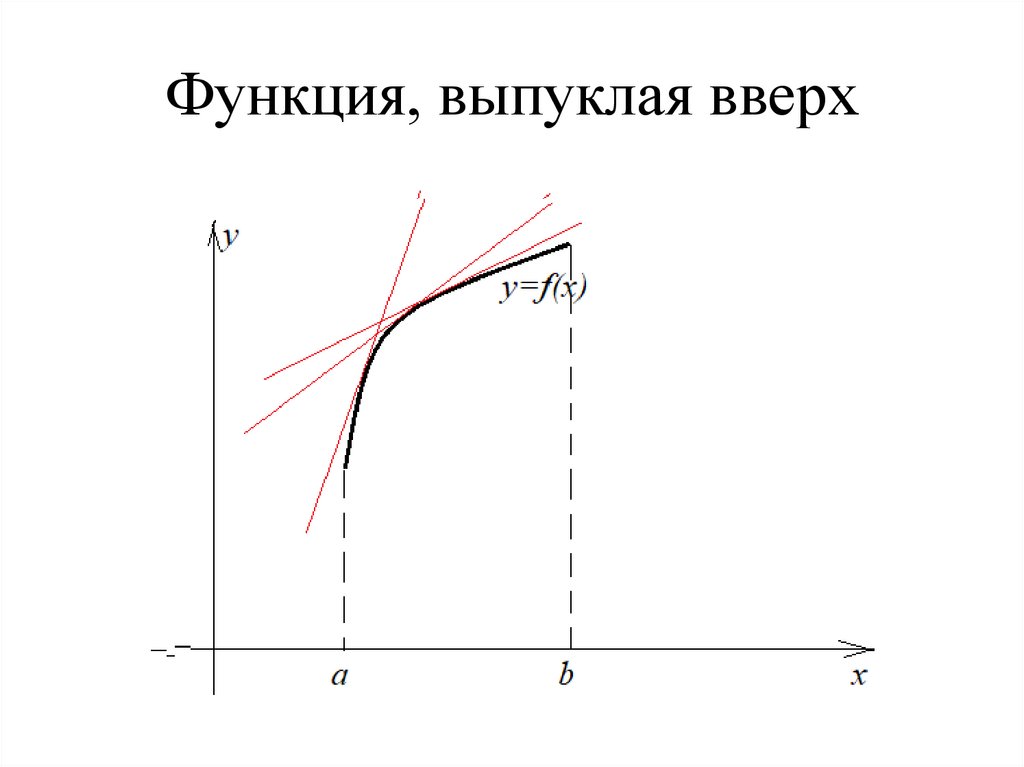
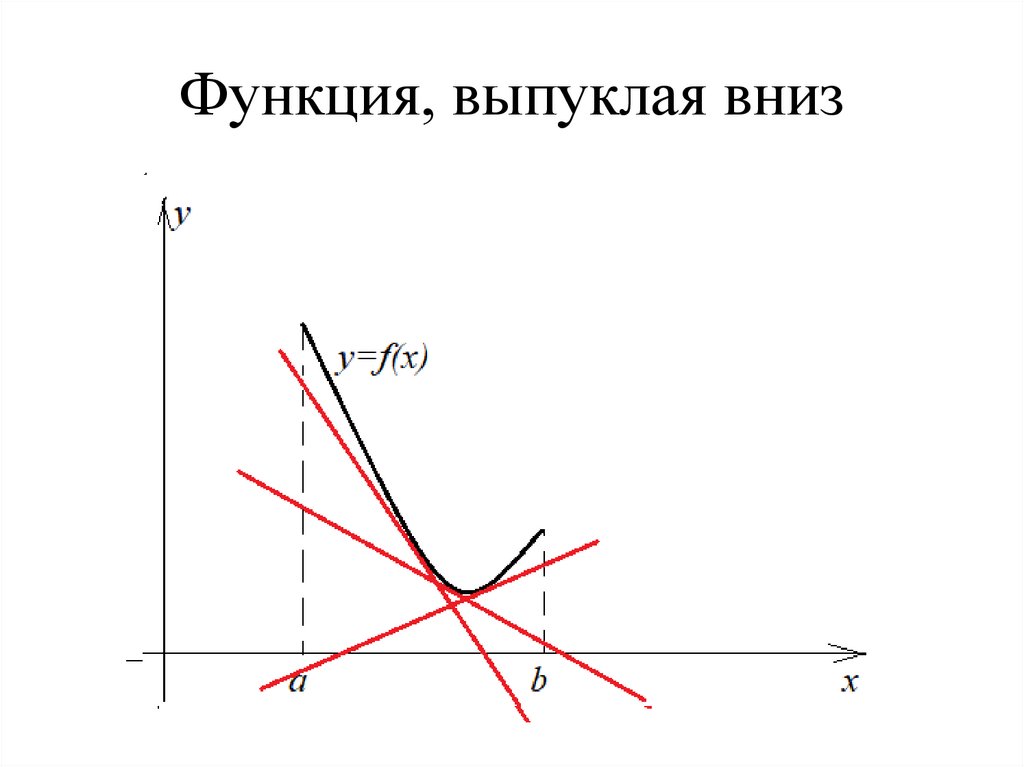
Основные определенияФункция у f (x) называется выпуклой вверх
(вниз) на промежутке a; b , если график
функции расположен ниже (выше) любой
касательной, проведенной к графику функции
в любой точке промежутка.
3.
Функция, выпуклая вверх4.
Функция, выпуклая вниз5.
Основные определенияТочка x 0 называется точкой перегиба графика
функции у f (x) , если в любой окрестности
точки x 0 есть точки графика функции у f (x
,)
расположенные как выше, так и ниже
касательной, проведенной к графику функции
у f (x) в точке с абсциссой x 0 .
6.
Необходимое условие точкиперегиба
Если точка x 0 является точкой перегиба
графика функции у f (x) , то вторая
производная функции, вычисленная в точке x 0
равна 0.
7.
Достаточное условие экстремумаПусть вторая производная функции у f (x)
в точке x 0 равна 0.
Точка x 0 является точкой перегиба графика
функции у f (x) , если при переходе через
точку x 0 вторая производная этой функции
меняет знак.
8.
Условия выпуклостиЕсли на промежутке a; b вторая производная
функции у f (x) положительна, то функция
у f (x)
на промежутке a; b выпукла
вниз.
Если на промежутке a; b вторая производная
функции у f (x) отрицательна, то функция
у f (x)
на промежутке a; b выпукла
вверх.
9.
ПримерИсследовать функцию
y x3 2 x 2 5x 4
на выпуклость, точки перегиба.
Решение.
Область определения: x R
10.
Примерy x 2 x 5x 4
3
2
Точки перегиба определяются второй
производной функции
2
y 3x 4 x 5
y 6 x 4
y 0 :
6 x 4 0;
2
x
3
11.
Примерy 6 x 4
2
– точка перегиба;
x
2
3
Функция выпукла вверх на ;
Функция выпукла вниз на
3
2
;
3









 mathematics
mathematics








