Случайные величины. Примеры случайных величин

1. Случайные величины

2. Случайная величина -

Случайная величина величина, которая в результате
опыта может принимать то или
иное числовое значение,
причем заранее не известно
какое именно.

3. Примеры случайных величин:

число детей, родившихся в течение
суток в г. Москве
количество бракованных изделий в
данной партии
число произведенных выстрелов до
первого попадания.
дальность полета артиллерийского
снаряда
расход электроэнергии предприятием за
месяц

4.

Случайные величины (СВ)
обозначаются большими латинскими
буквами X, Y, Z
Принимаемые ими значения - малыми
прописными буквами x, y, z … .

5. Дискретной случайной величиной (ДСВ)

называется такая величина, которая в
результате опыта может принимать
определенные значения с определенной
вероятностью, образующие счетное
множество (множество, элементы
которого могут быть занумерованы).
Это множество может быть как
конечным, так и бесконечным.

6. Примеры ДСВ

количество выстрелов до первого
попадания в цель является дискретной
случайной величиной, т.к. эта величина
может принимать и бесконечное, хотя и
счетное количество значений.
число детей, родившихся в течение
суток в г. Москве
количество бракованных изделий в
данной партии

7. Непрерывной случайной величиной (НСВ)

называется такая величина, которая
может принимать любые значения из
некоторого конечного или бесконечного
промежутка.
дальность полета артиллерийского
снаряда
расход электроэнергии предприятием за
месяц
время безотказной работы прибора

8. Закон распределения ДСВ

Соотношение между возможными
значениями случайной величины и их
вероятностями называется законом
распределения дискретной
случайной величины.
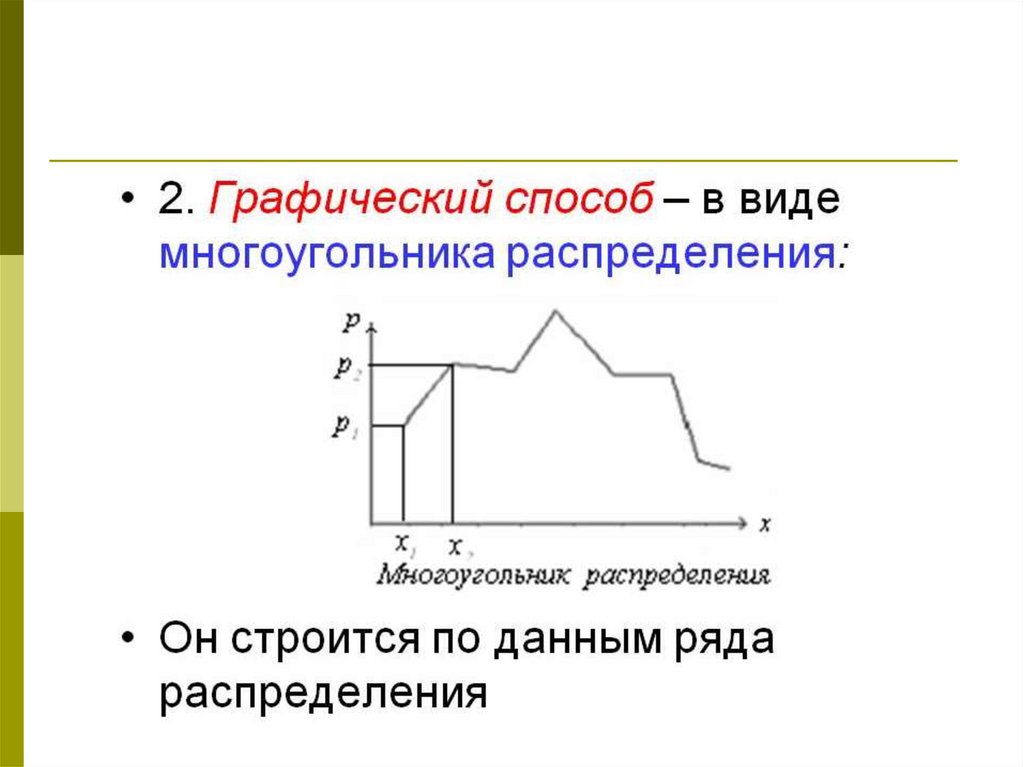
Закон распределения может быть задан
аналитически, в виде таблицы или
графически.
Таблица соответствия значений
случайной величины и их вероятностей
называется рядом распределения.

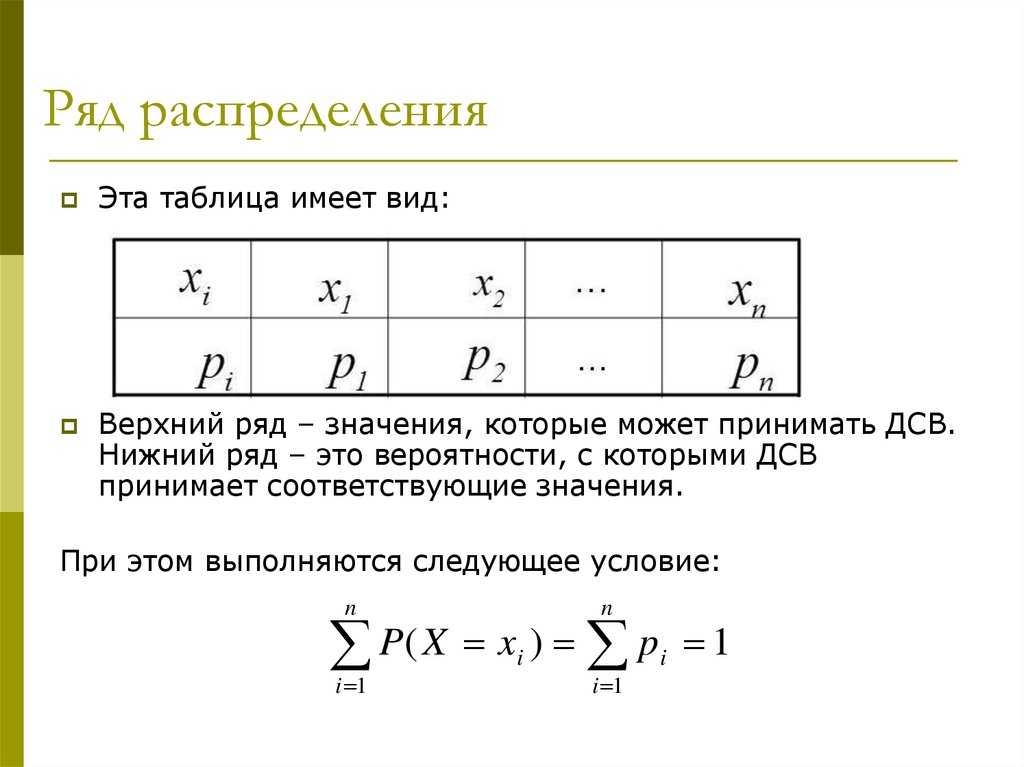
9. Ряд распределения

Эта таблица имеет вид:
Верхний ряд – значения, которые может принимать ДСВ.
Нижний ряд – это вероятности, с которыми ДСВ
принимает соответствующие значения.
При этом выполняются следующее условие:
n
n
P( X x ) p 1
i 1
i
i 1
i

10.

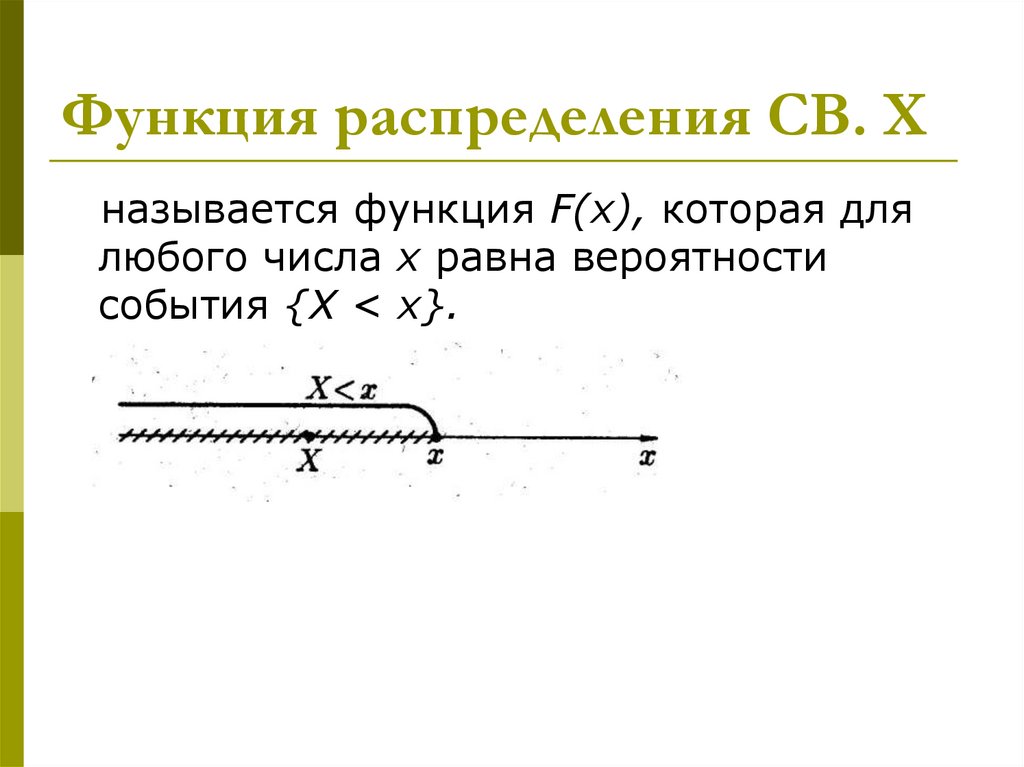
11. Функция распределения СВ. X

называется функция F(х), которая для
любого числа х равна вероятности
события {X < х}.

12. Свойства

Функция распределения обладает следующими
свойствами:
1.
F(х) ограничена, т. е.
2. F(х) — неубывающая функция на R, т. е.
если х1 > х2 то F(x1)>= F(x2)
3. F(х) обращает в ноль на минус
бесконечности и равна единице в плюс
бесконечности
4. Вероятность попадания с. в. X в промежуток
[а, b) равна приращению ее функции
распределения на этом промежутке, т. е.
р(а < X <b)= F(b)-F(а).
5. F(х) непрерывна слева.

13. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Построить закон распределения случайной

величины Х - числа попадания в
цель и многоугольник распределения

14. Пример 2.

На элеватор прибыло 6
машин агрофирмы
«А1» и 9 машин агрофирмы «А2». Под
разгрузку случайным образом загоняются
6 машин. Число машин фирмы «А1»,
попавших под разгрузку - случайная
величина.
1) составить ряд распределения этой
случайной величины и построить его
многоугольник.
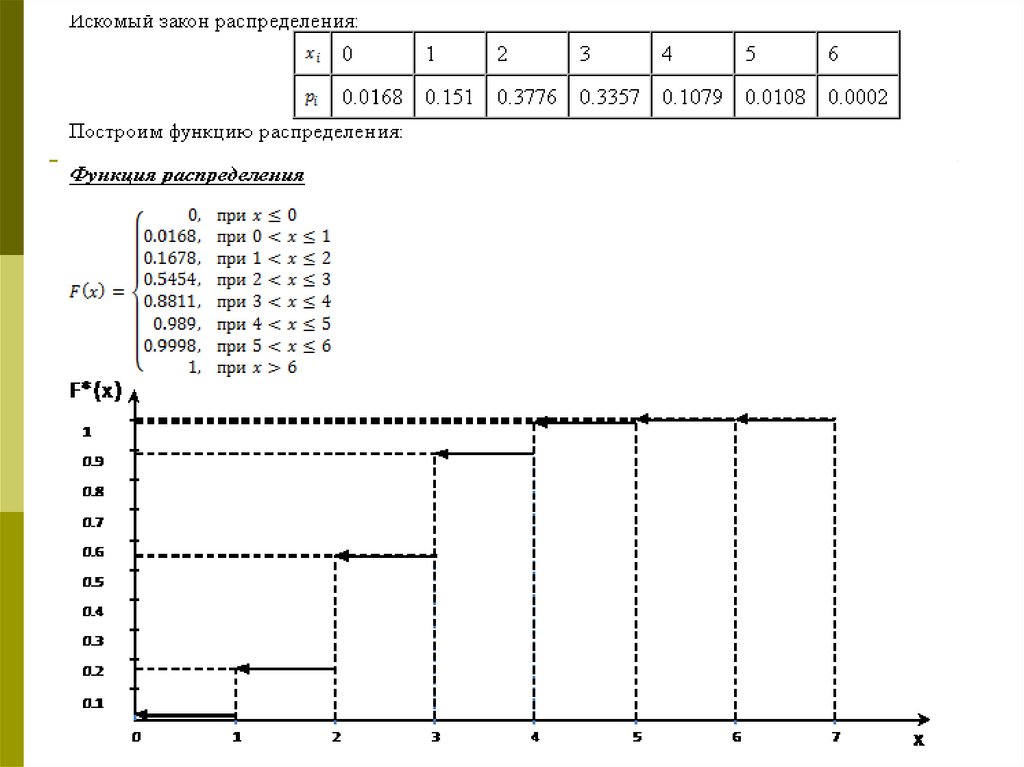
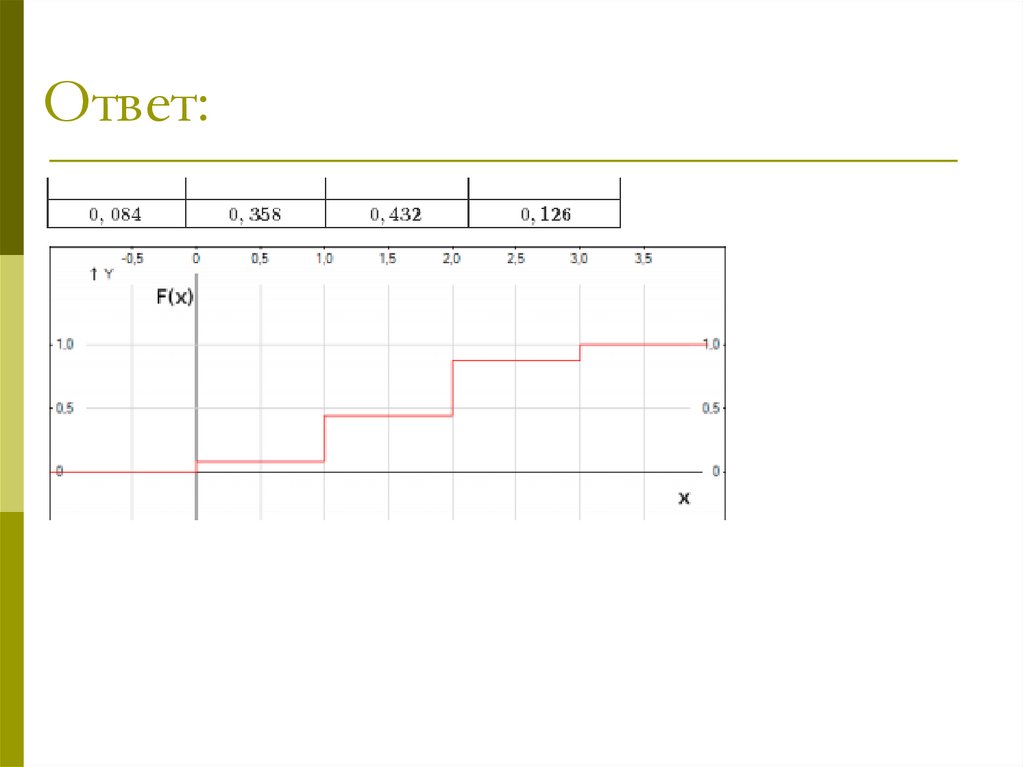
2) найти функцию распределения и
построить ее график.

15.

16. Пример 3.

Три стрелка независимо друг от друга
стреляют каждый по своей мишени один
раз. Вероятности попадания при одном
выстреле у стрелка равны
соответственно р1=0.3, р2=0.6, р3=0.7 .
Построить ряд распределения и
многоугольник, найти функцию
распределения и ее график для
случайной величины, равной числу
попаданий в мишени.

17. Ответ: