Степень вершины графа

1.

Степень
вершины графа

2.

Вспоминаем
то, что знаем

3.

Что такое граф?

4.

Что такое граф?
Граф – изображение объектов и связей
между ними с помощью точек и линий.

5.

Как называются точки в графе?

6.

Как называются точки в графе?
Точки в графе называются вершинами.

7.

Как называются линии в графе?

8.

Как называются линии в графе?
Линии в графе называются рёбрами.

9.

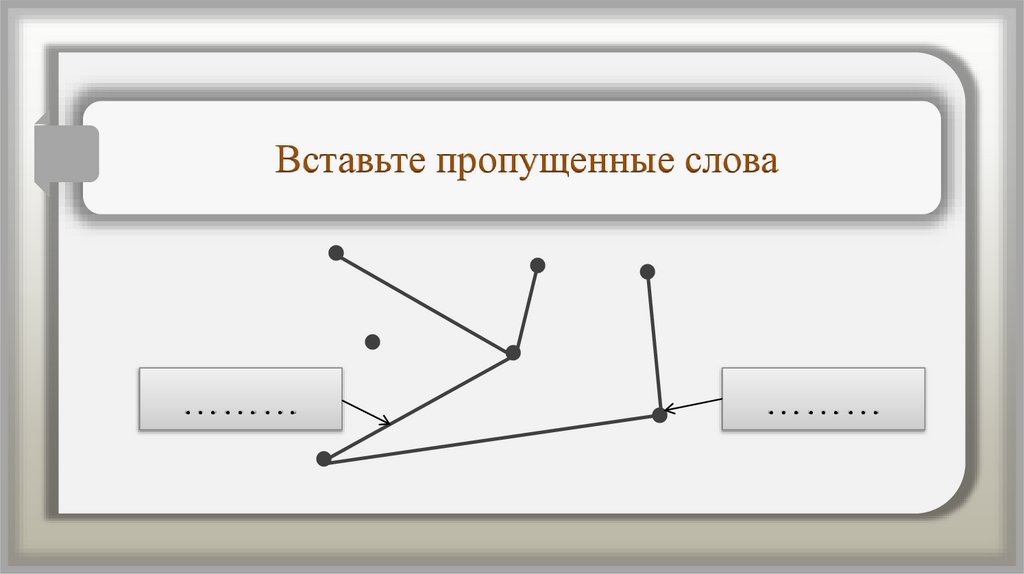
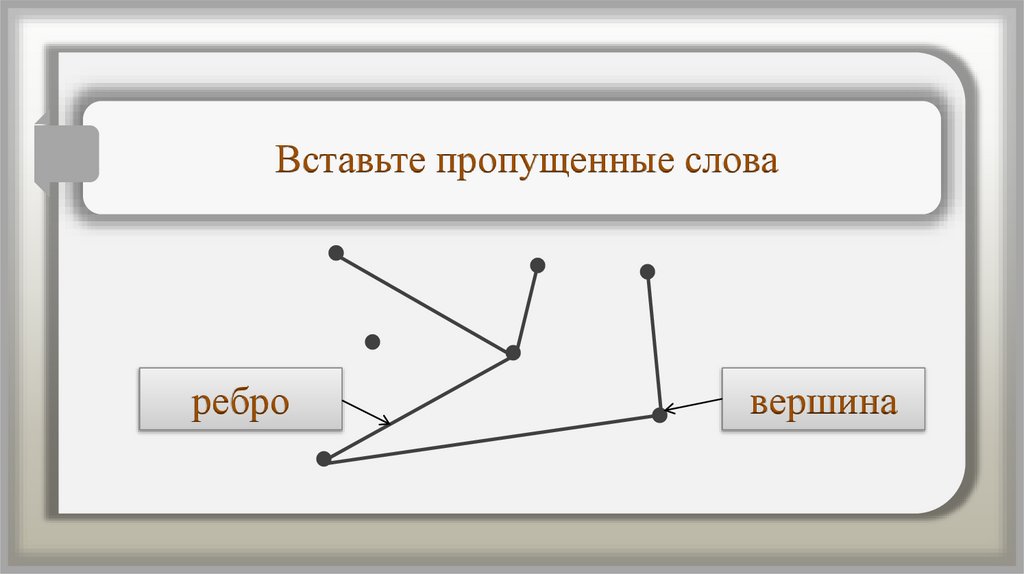
Вставьте пропущенные слова
………
………

10.

Вставьте пропущенные слова
ребро
вершина

11.

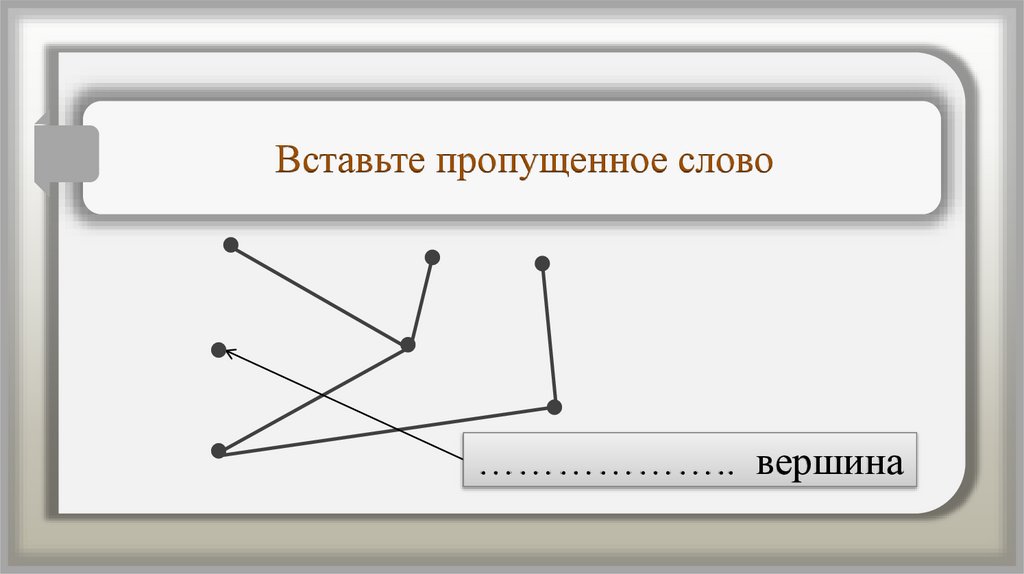
Вставьте пропущенное слово
……………….. вершина

12.

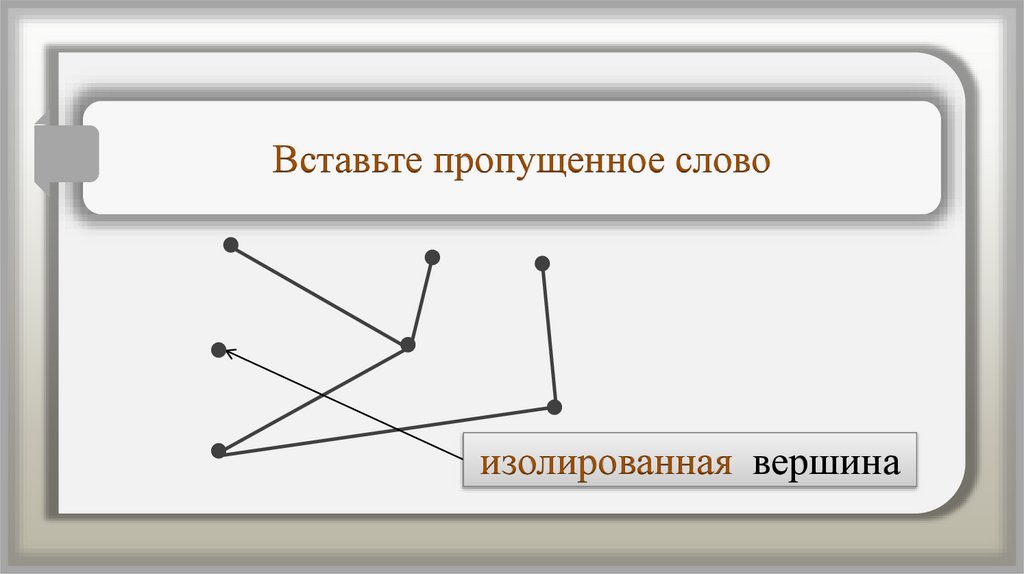
Вставьте пропущенное слово
изолированная вершина

13.

Открываем
новые знания

14.

Степень
вершины графа

15.

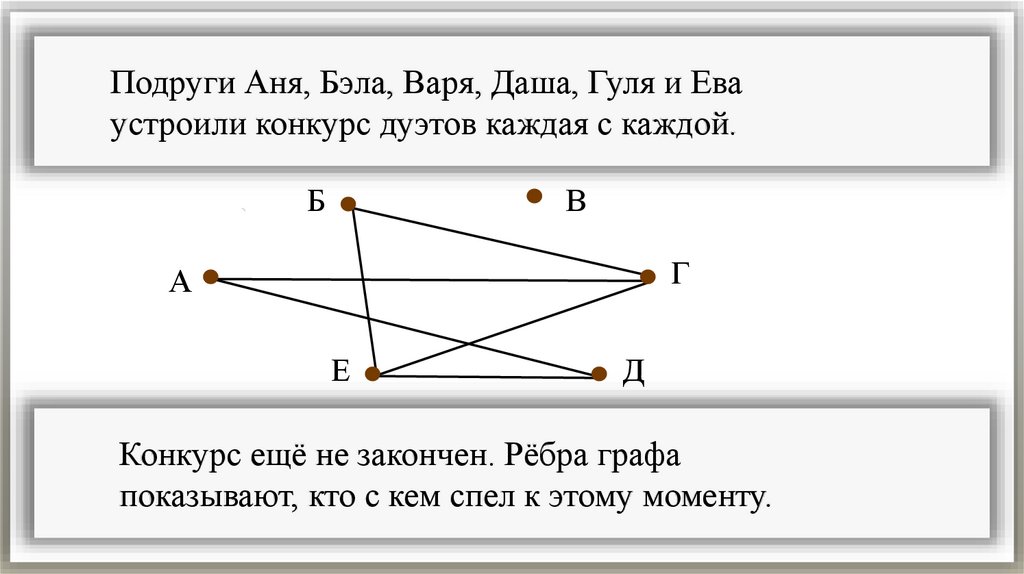
Подруги Аня, Бэла, Варя, Даша, Гуля и Ева
устроили конкурс дуэтов каждая с каждой.
Б
В
Г
А
Е
Д
Конкурс ещё не закончен. Рёбра графа
показывают, кто с кем спел к этому моменту.

16.

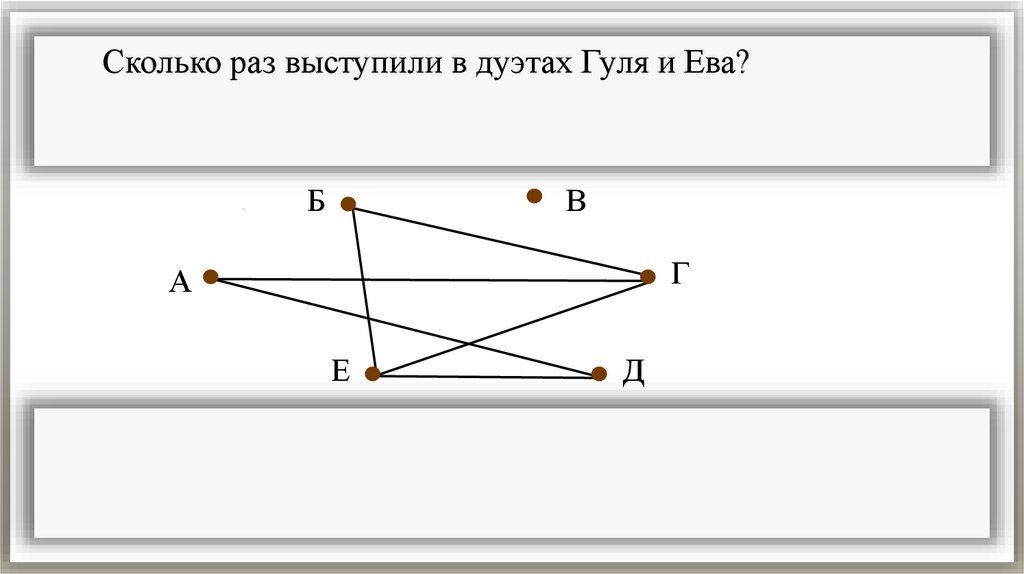
Сколько раз выступили в дуэтах Гуля и Ева?
Б
В
Г
А
Е
Д

17.

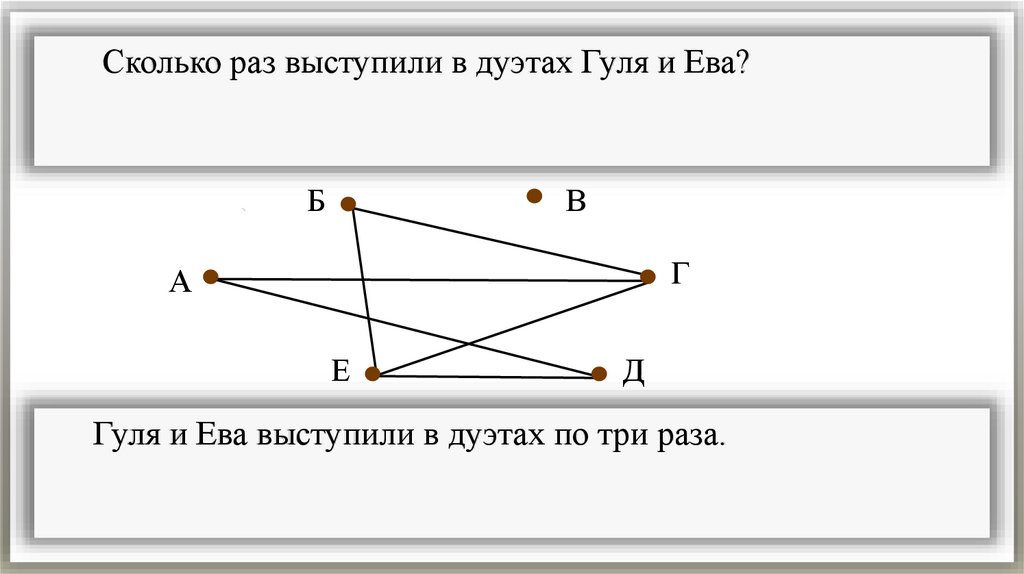
Сколько раз выступили в дуэтах Гуля и Ева?
Б
В
Г
А
Е
Д
Гуля и Ева выступили в дуэтах по три раза.

18.

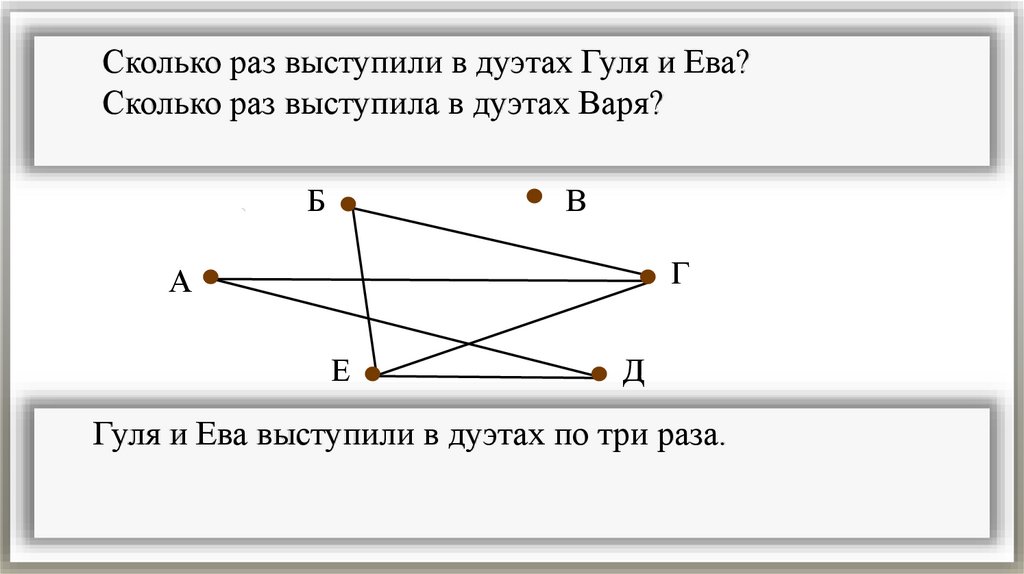
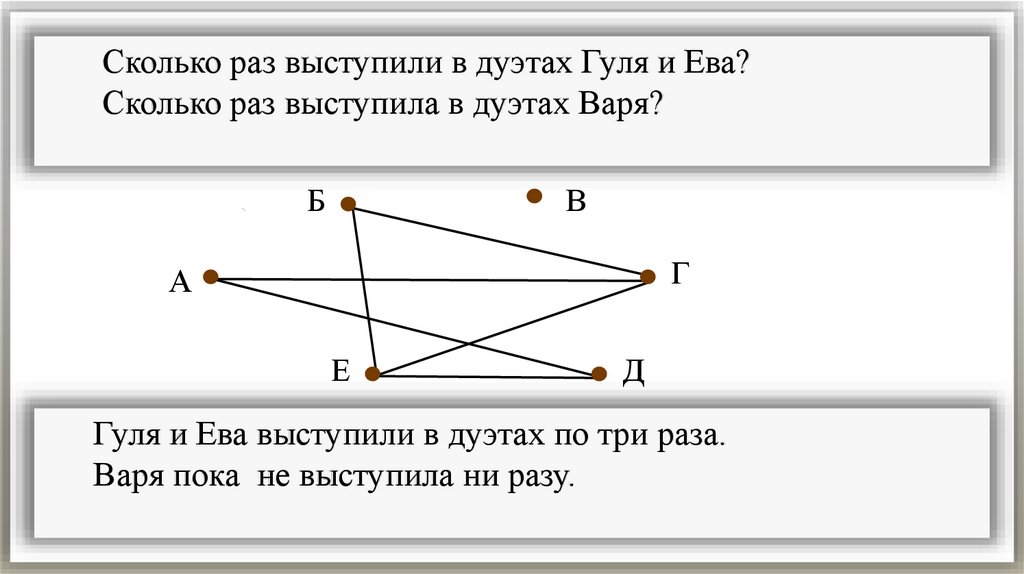
Сколько раз выступили в дуэтах Гуля и Ева?
Сколько раз выступила в дуэтах Варя?
Б
В
Г
А
Е
Д
Гуля и Ева выступили в дуэтах по три раза.

19.

Сколько раз выступили в дуэтах Гуля и Ева?
Сколько раз выступила в дуэтах Варя?
Б
В
Г
А
Е
Д
Гуля и Ева выступили в дуэтах по три раза.
Варя пока не выступила ни разу.

20.

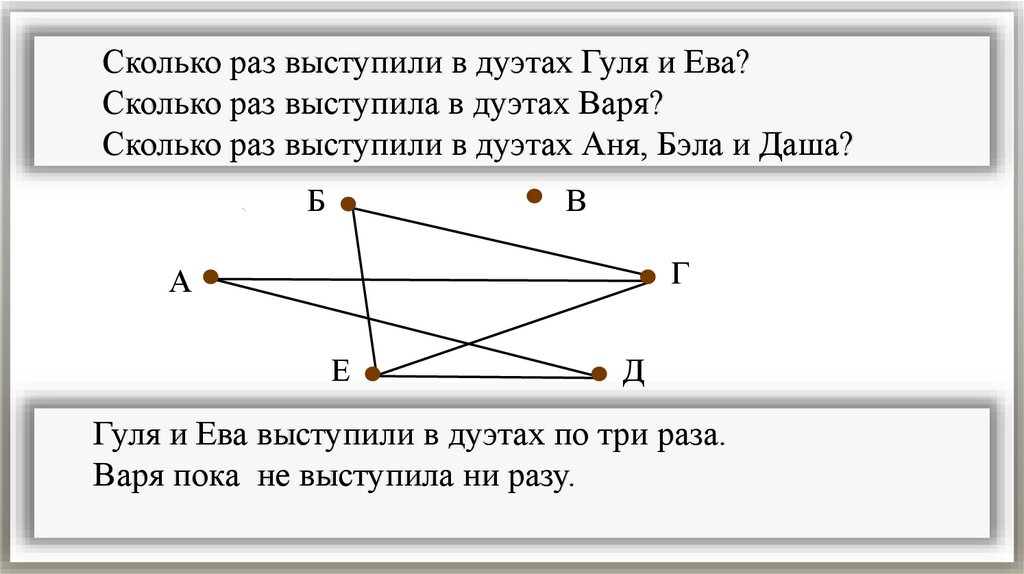
Сколько раз выступили в дуэтах Гуля и Ева?
Сколько раз выступила в дуэтах Варя?
Сколько раз выступили в дуэтах Аня, Бэла и Даша?
Б
В
Г
А
Е
Д
Гуля и Ева выступили в дуэтах по три раза.
Варя пока не выступила ни разу.

21.

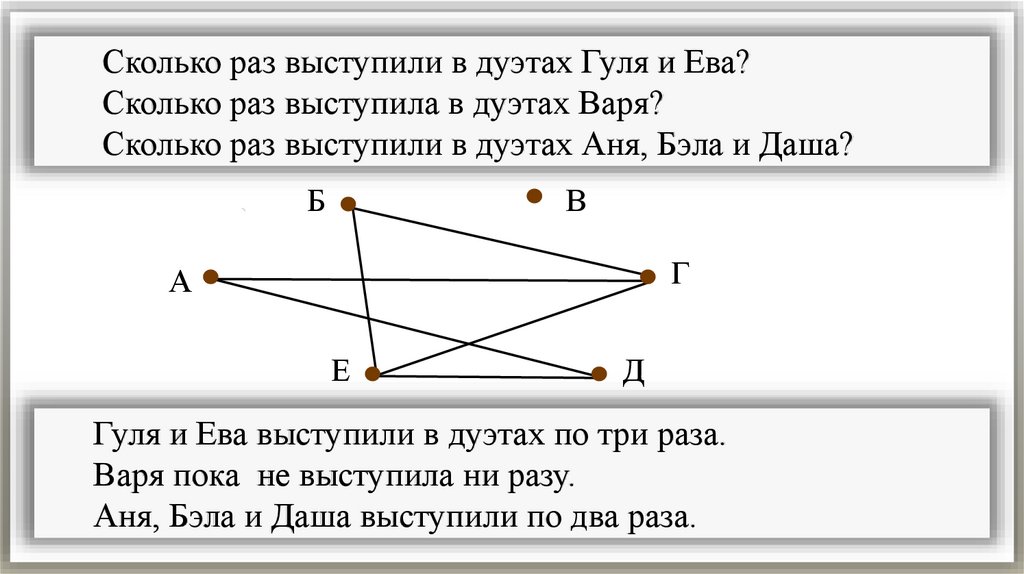
Сколько раз выступили в дуэтах Гуля и Ева?
Сколько раз выступила в дуэтах Варя?
Сколько раз выступили в дуэтах Аня, Бэла и Даша?
Б
В
Г
А
Е
Д
Гуля и Ева выступили в дуэтах по три раза.
Варя пока не выступила ни разу.
Аня, Бэла и Даша выступили по два раза.

22.

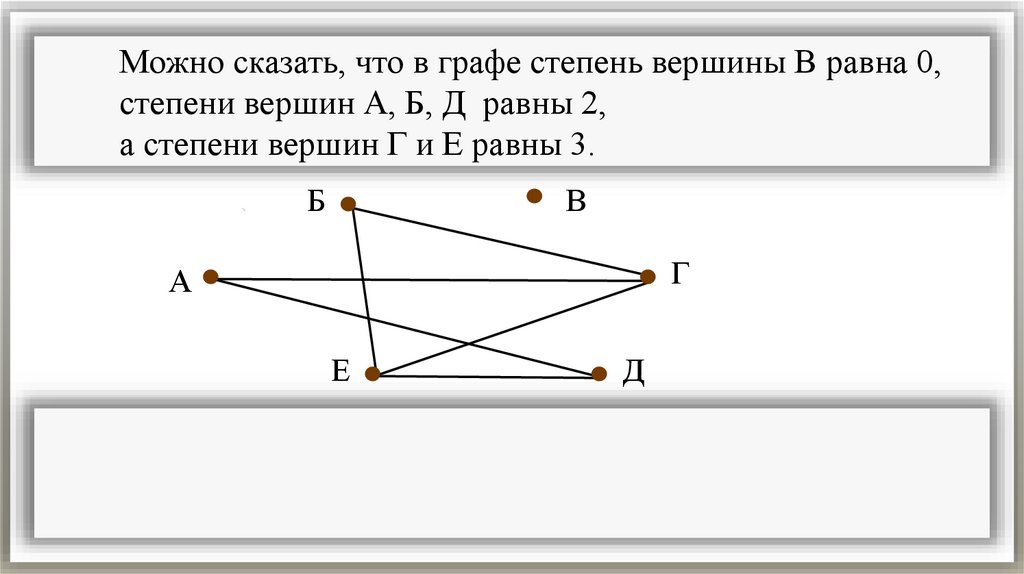
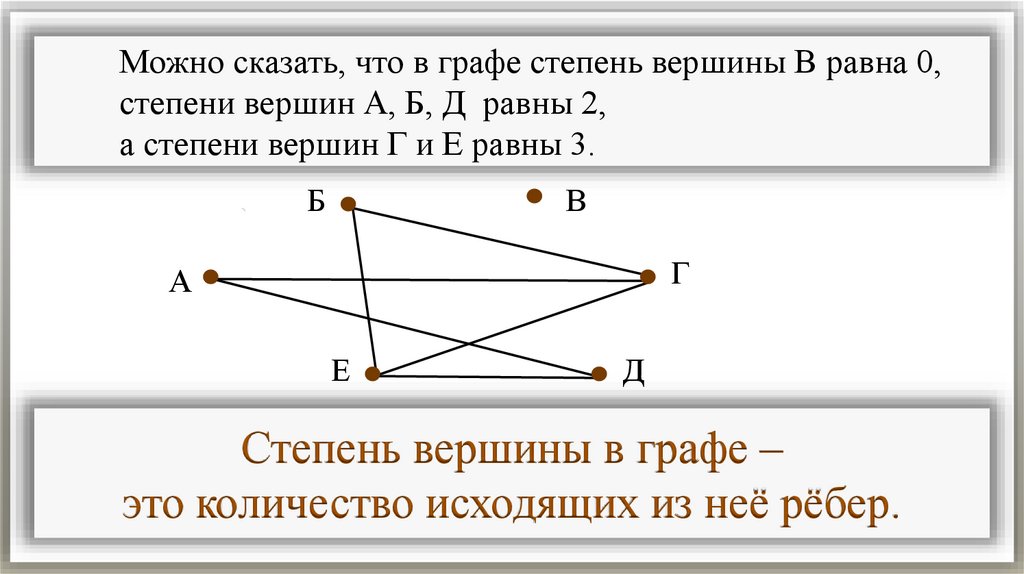
Можно сказать, что в графе степень вершины В равна 0,
степени вершин А, Б, Д равны 2,
а степени вершин Г и Е равны 3.
Б
В
Г
А
Е
Д

23.

Можно сказать, что в графе степень вершины В равна 0,
степени вершин А, Б, Д равны 2,
а степени вершин Г и Е равны 3.
Б
В
Г
А
Е
Д
Степень вершины в графе –
это количество исходящих из неё рёбер.

24.

Граф с петлёй

25.

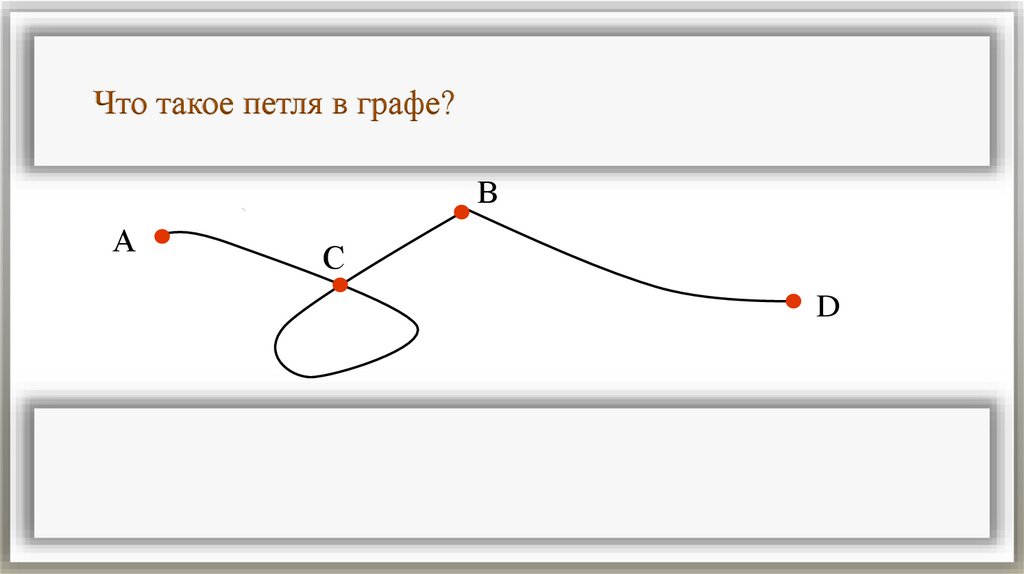
Что такое петля в графе?
В
А
С
D

26.

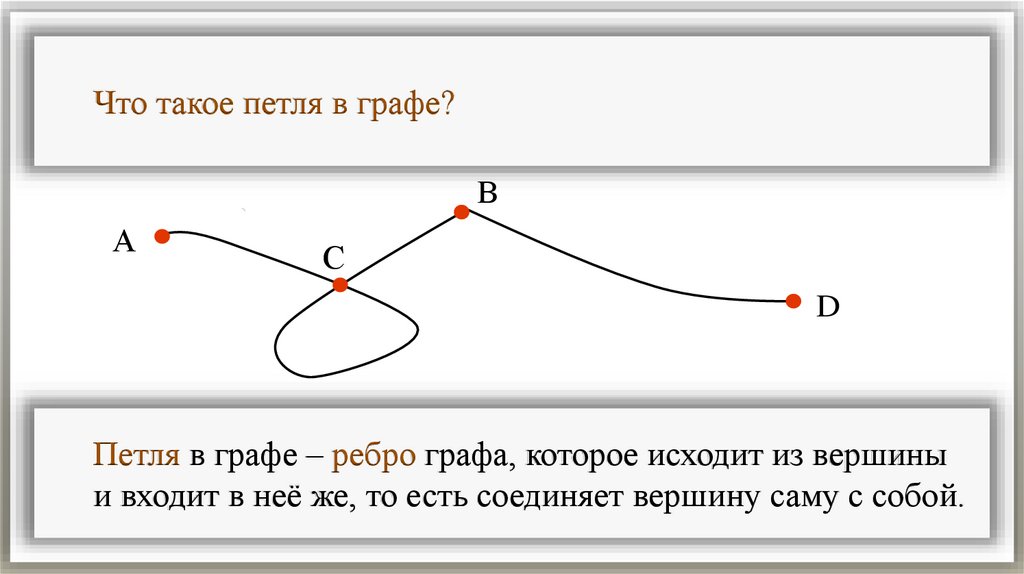
Что такое петля в графе?
В
А
С
D
Петля в графе – ребро графа, которое исходит из вершины
и входит в неё же, то есть соединяет вершину саму с собой.

27.

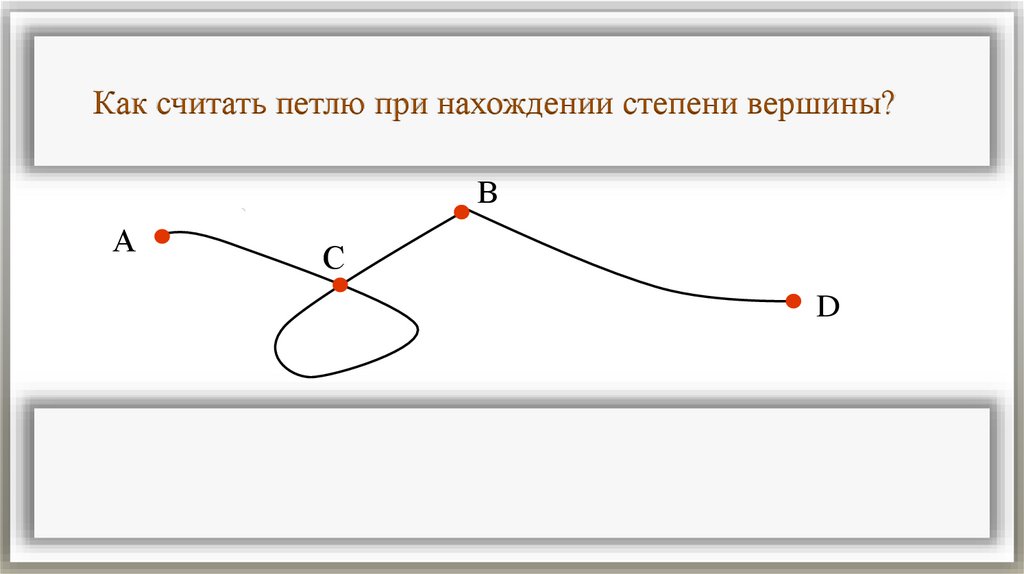
Как считать петлю при нахождении степени вершины?
В
А
С
D

28.

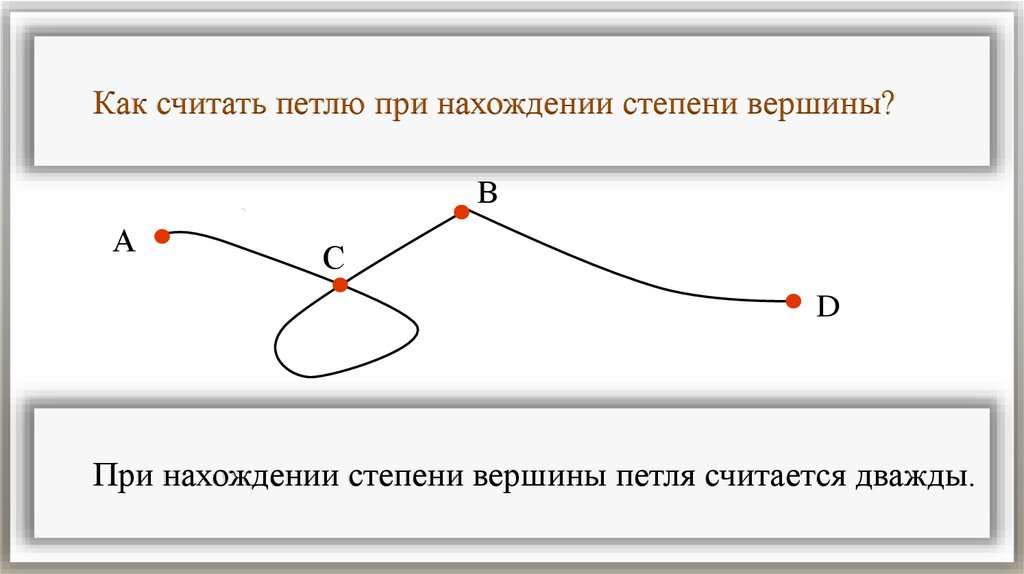
Как считать петлю при нахождении степени вершины?
В
А
С
D
При нахождении степени вершины петля считается дважды.

29.

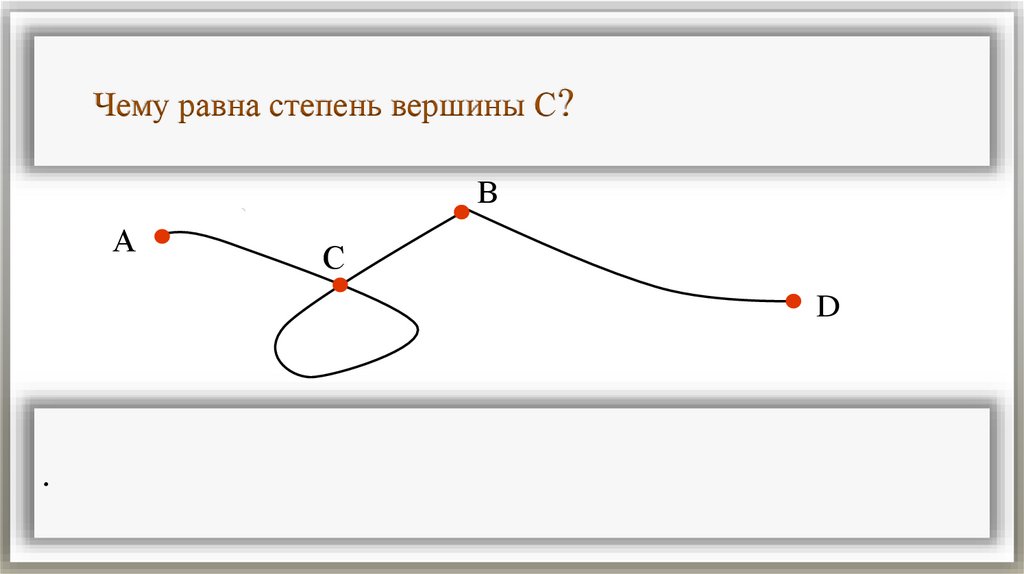
Чему равна степень вершины С?
В
А
С
D
.

30.

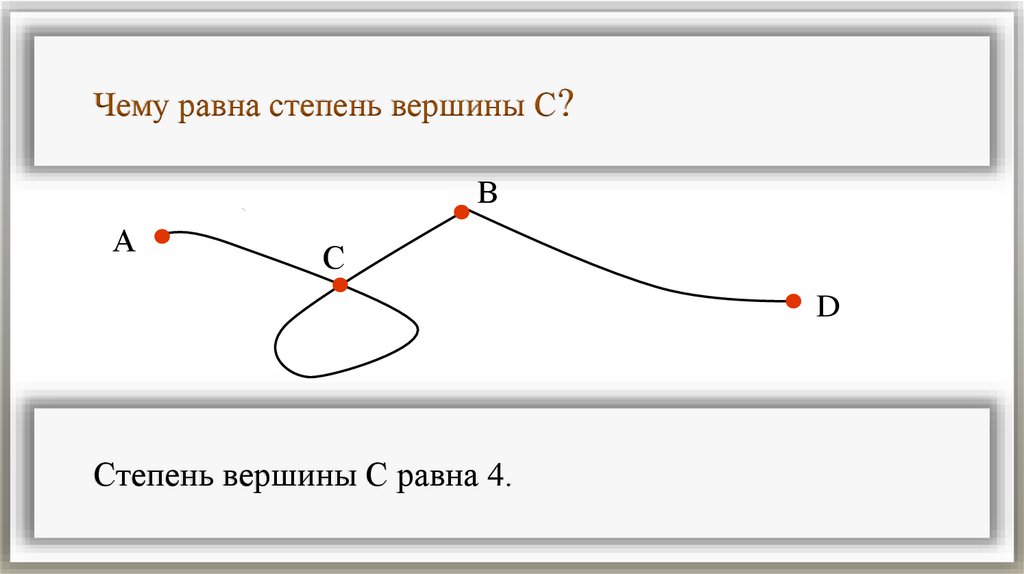
Чему равна степень вершины С?
В
А
С
D
Степень вершины С равна 4.

31.

Сравнение графов
по степеням вершин

32.

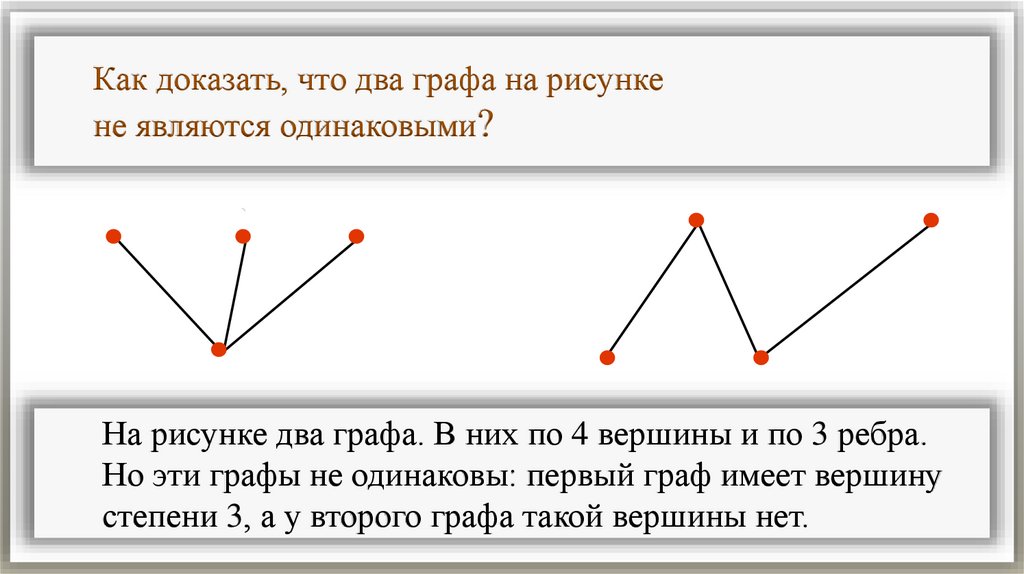
Как доказать, что два графа на рисунке
не являются одинаковыми?

33.

Как доказать, что два графа на рисунке
не являются одинаковыми?
На рисунке два графа. В них по 4 вершины и по 3 ребра.
Но эти графы не одинаковы: первый граф имеет вершину
степени 3, а у второго графа такой вершины нет.

34.

Теорема о сумме
степеней вершин графа

35.

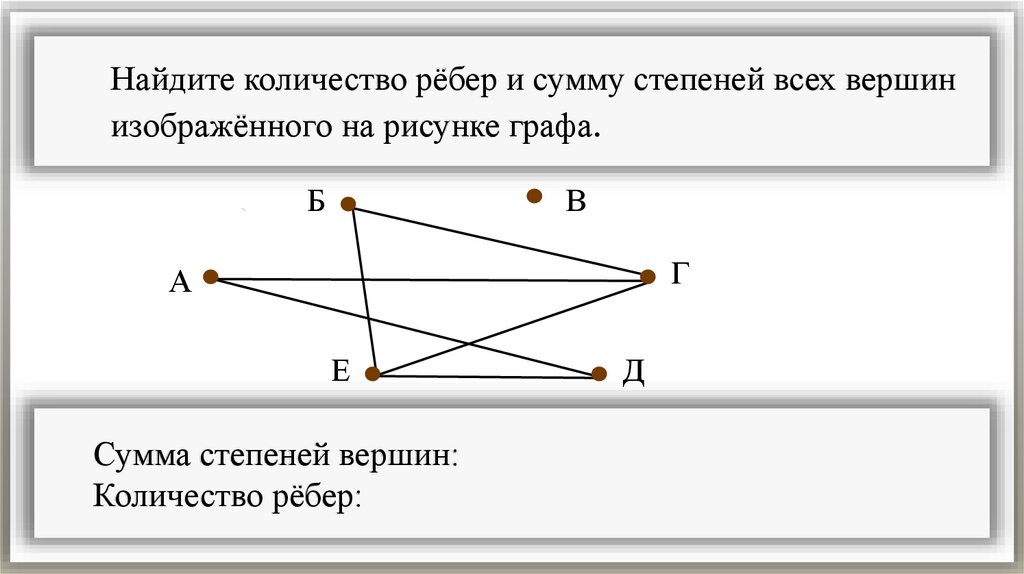
Найдите количество рёбер и сумму степеней всех вершин
изображённого на рисунке графа.
Б
В
Г
А
Е
Сумма степеней вершин:
Количество рёбер:
Д

36.

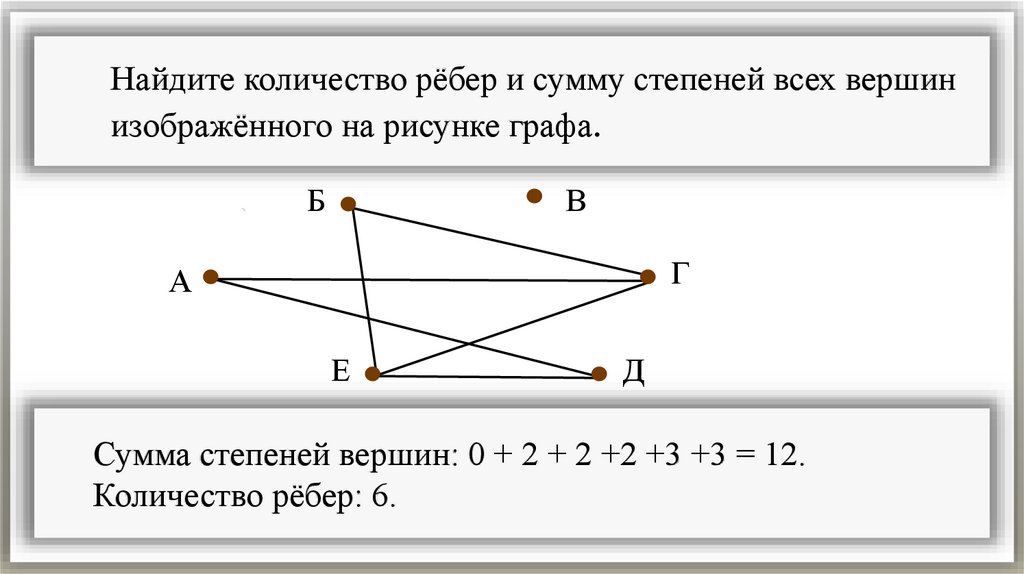
Найдите количество рёбер и сумму степеней всех вершин
изображённого на рисунке графа.
Б
В
Г
А
Е
Д
Сумма степеней вершин: 0 + 2 + 2 +2 +3 +3 = 12.
Количество рёбер: 6.

37.

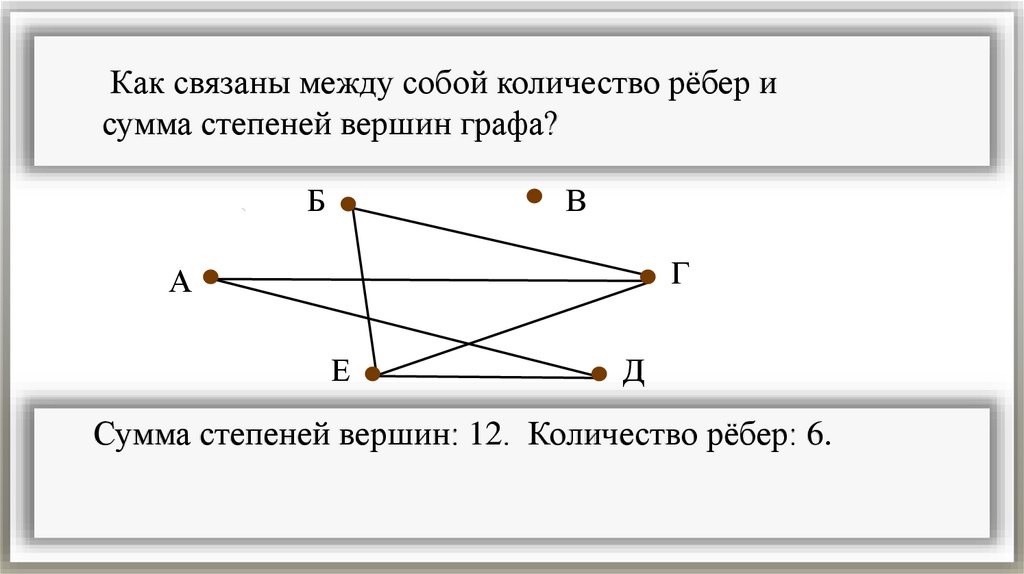
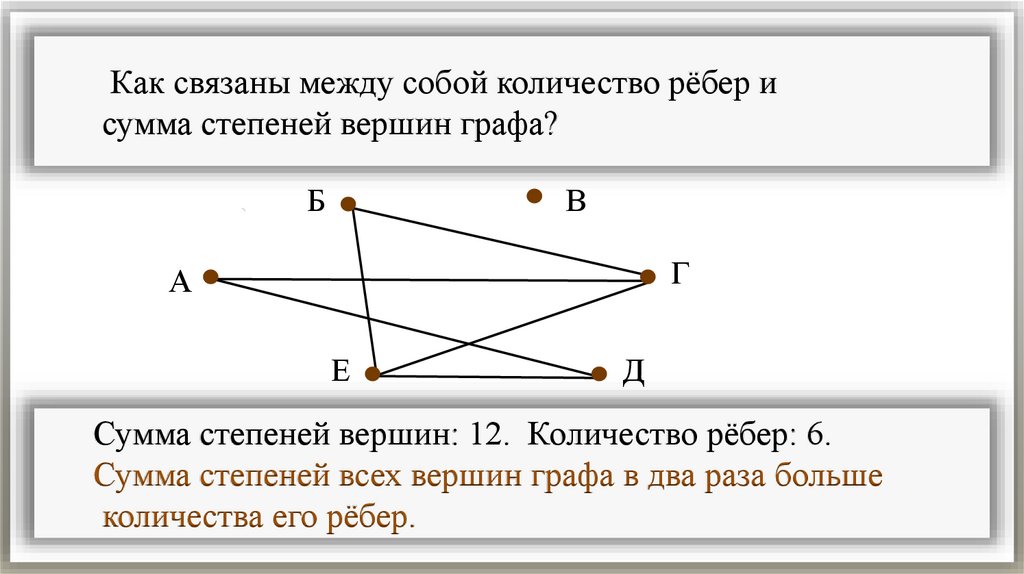
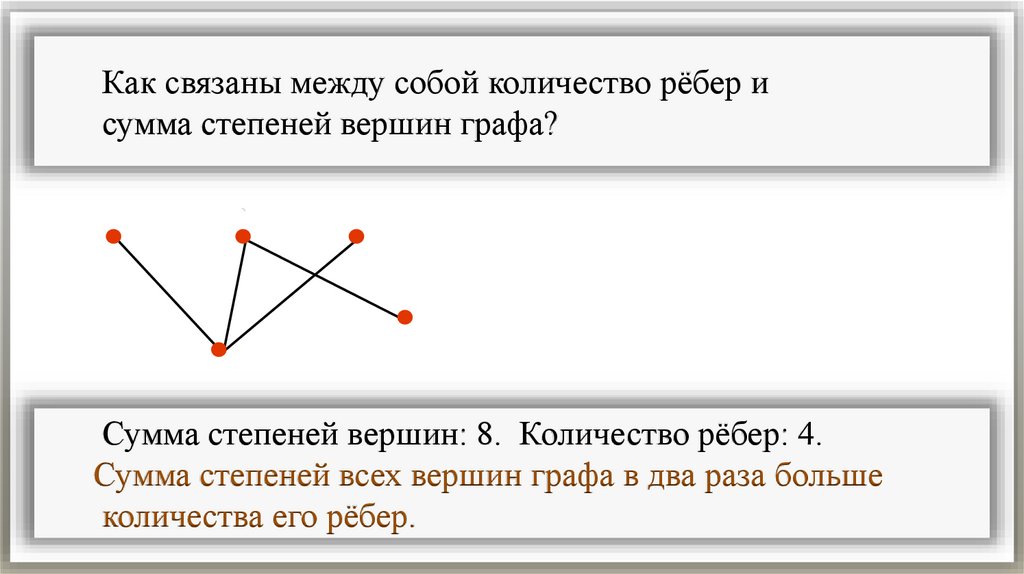
Как связаны между собой количество рёбер и
сумма степеней вершин графа?
Б
В
Г
А
Е
Д
Сумма степеней вершин: 12. Количество рёбер: 6.

38.

Как связаны между собой количество рёбер и
сумма степеней вершин графа?
Б
В
Г
А
Е
Д
Сумма степеней вершин: 12. Количество рёбер: 6.
Сумма степеней всех вершин графа в два раза больше
количества его рёбер.

39.

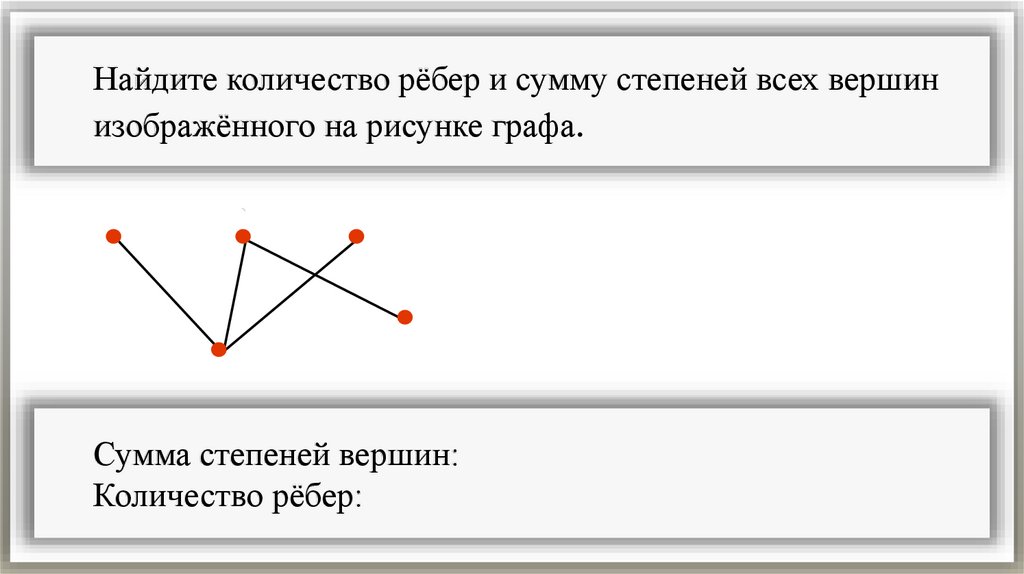
Найдите количество рёбер и сумму степеней всех вершин
изображённого на рисунке графа.
Сумма степеней вершин:
Количество рёбер:

40.

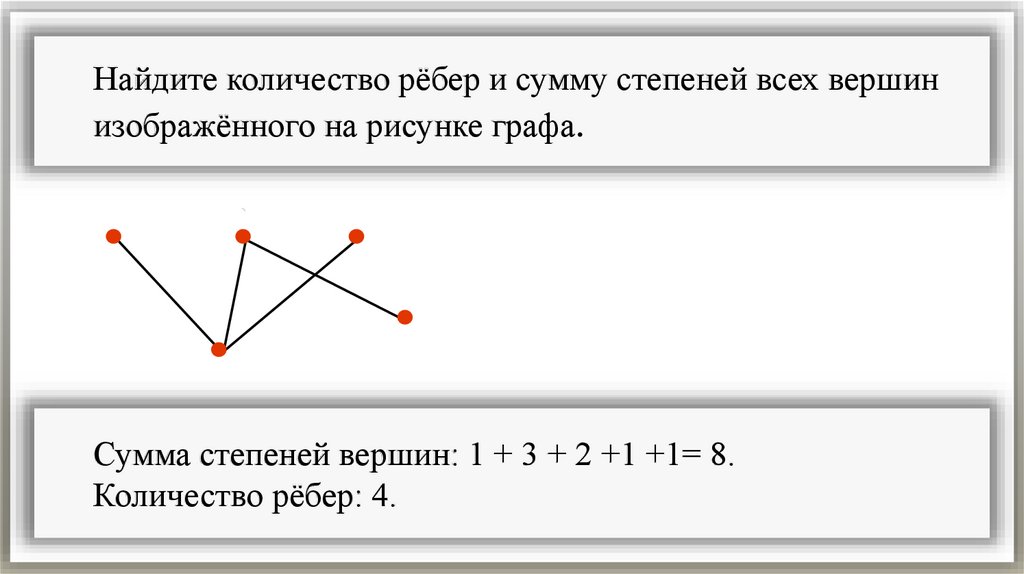
Найдите количество рёбер и сумму степеней всех вершин
изображённого на рисунке графа.
Сумма степеней вершин: 1 + 3 + 2 +1 +1= 8.
Количество рёбер: 4.

41.

Как связаны между собой количество рёбер и
сумма степеней вершин графа?
Сумма степеней вершин: 8. Количество рёбер: 4.

42.

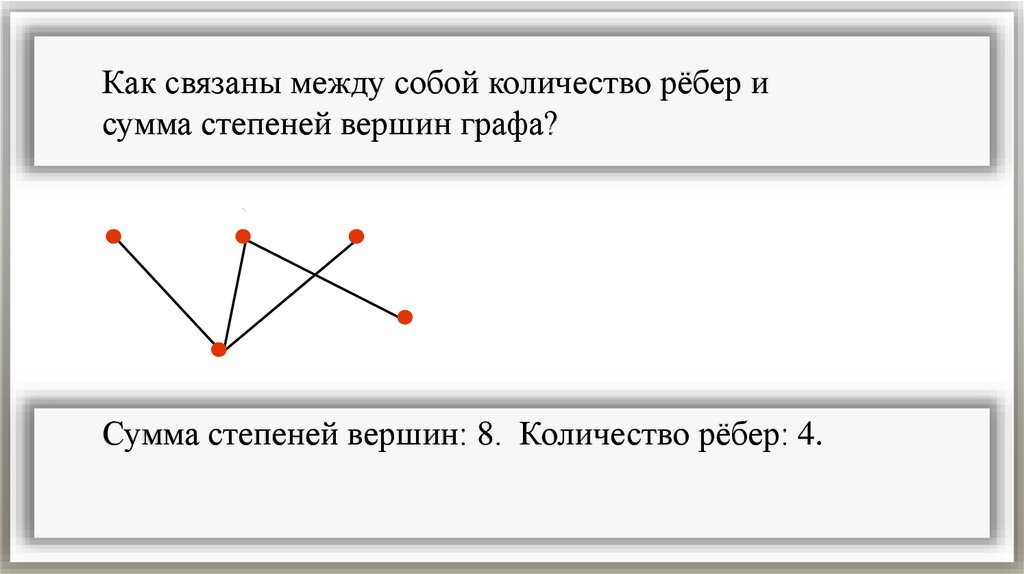
Как связаны между собой количество рёбер и
сумма степеней вершин графа?
Сумма степеней вершин: 8. Количество рёбер: 4.
Сумма степеней всех вершин графа в два раза больше
количества его рёбер.

43.

Сумма степеней всех вершин графа
в два раза больше количества его рёбер.
Сумма степеней вершин
Количество рёбер =
2
В любом графе сумма степеней всех его
вершин является чётным числом.

44.

Развиваем умения

45.

Тест

46.

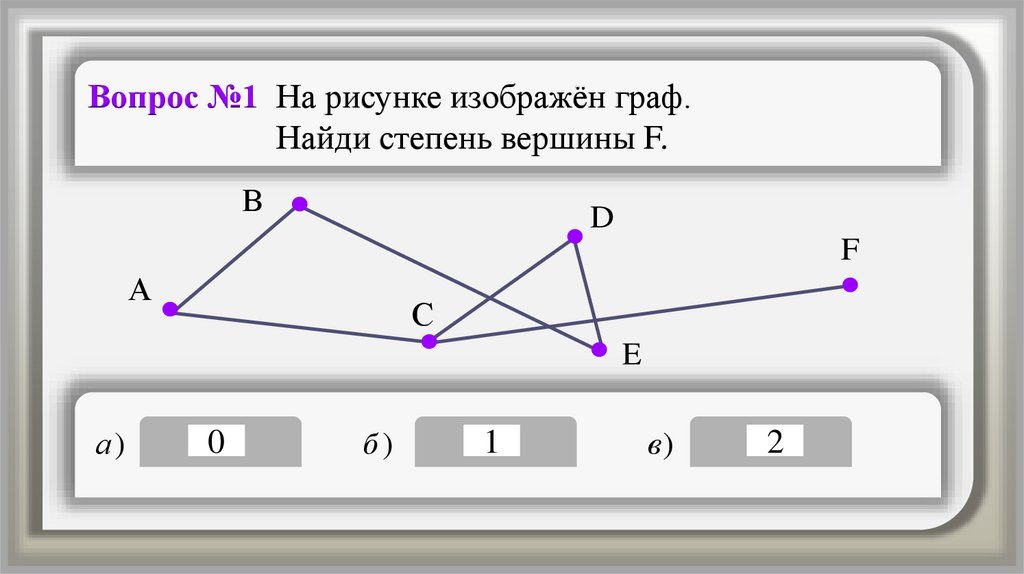
Вопрос №1 На рисунке изображён граф.
Найди степень вершины F.
В
D
F
А
С
E
а)
0
б)
1
в)
2

47.

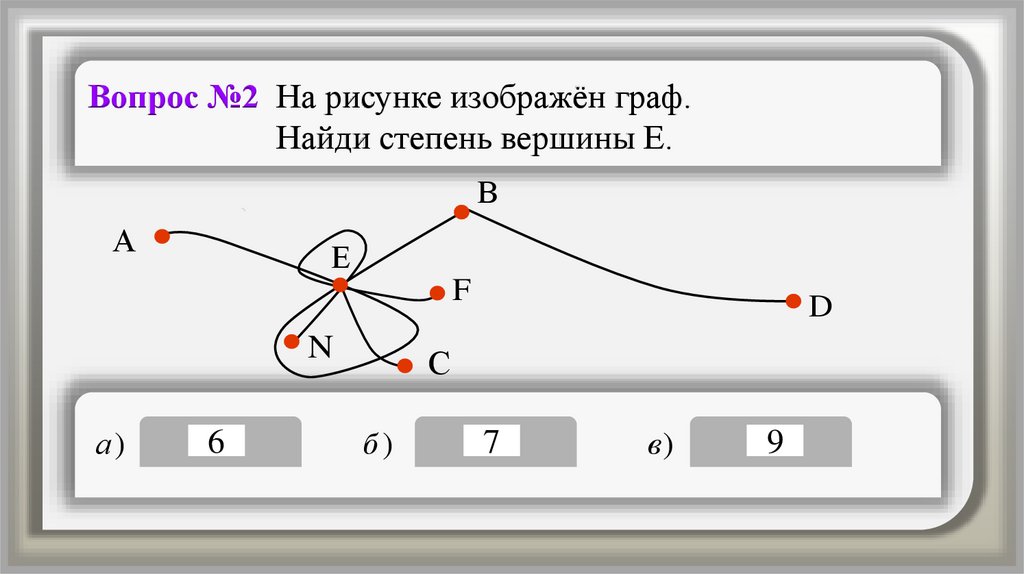
Вопрос №2 На рисунке изображён граф.
Найди степень вершины Е.
В
А
Е
F
N
а)
6
D
С
б)
7
в)
9

48.

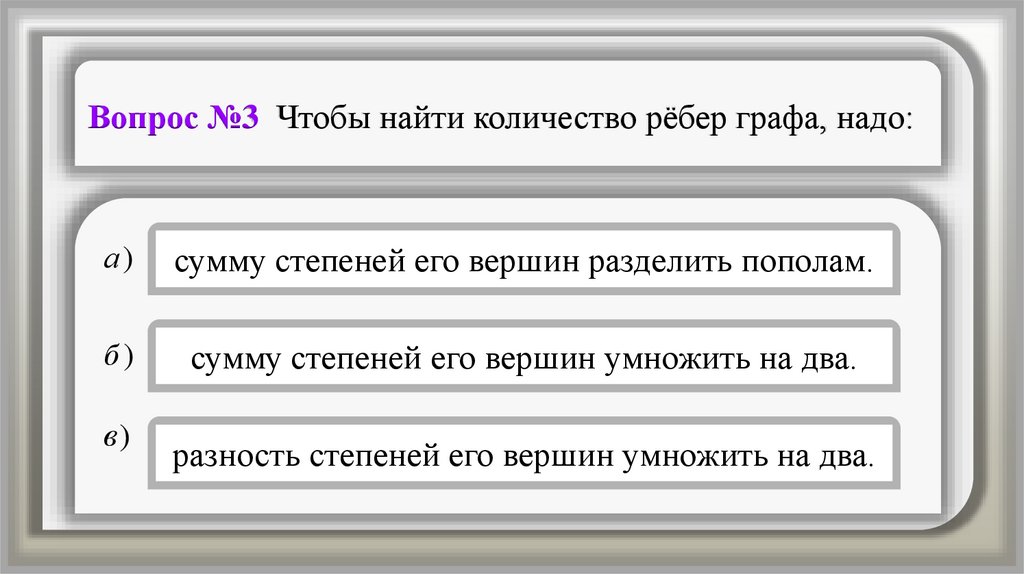
Вопрос №3 Чтобы найти количество рёбер графа, надо:
а)
сумму степеней его вершин разделить пополам.
б)
сумму степеней его вершин умножить на два.
в)
разность степеней его вершин умножить на два.

49.

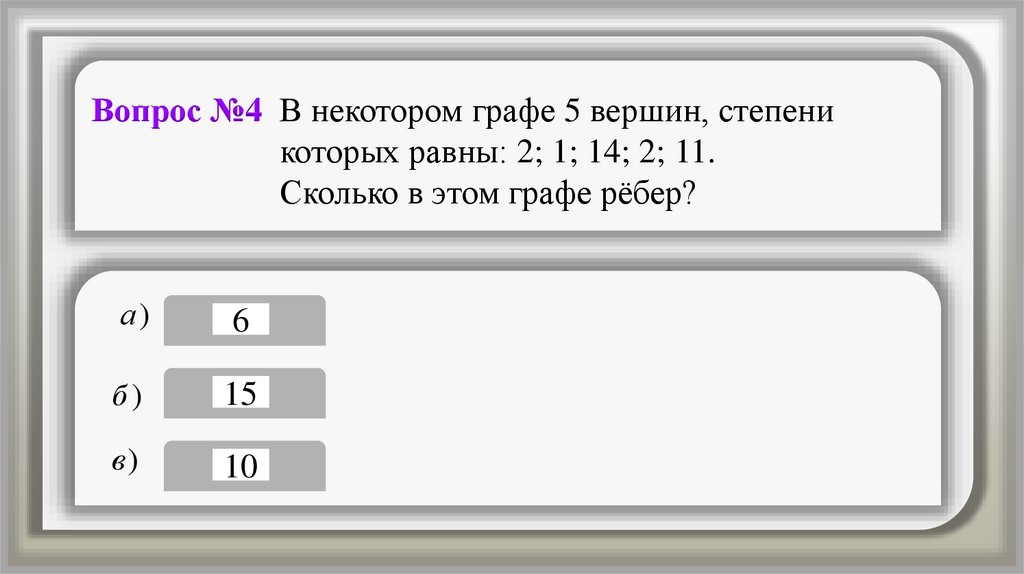
Вопрос №4 В некотором графе 5 вершин, степени
которых равны: 2; 1; 14; 2; 11.
Сколько в этом графе рёбер?
а)
6
б)
15
в)
10

50.

Вопрос №5 В графе шесть вершин имеют
степень 5, четыре вершины − степень 6.
Сколько рёбер в этом графе?
а)
54
б)
27
в)
108

51.

Вопрос №6 В графе все степени вершин равны.
Вершин у него 26, а рёбер 78.
Чему равна степень любой вершины этого графа?
а)
4
б)
8
в)
6

52.

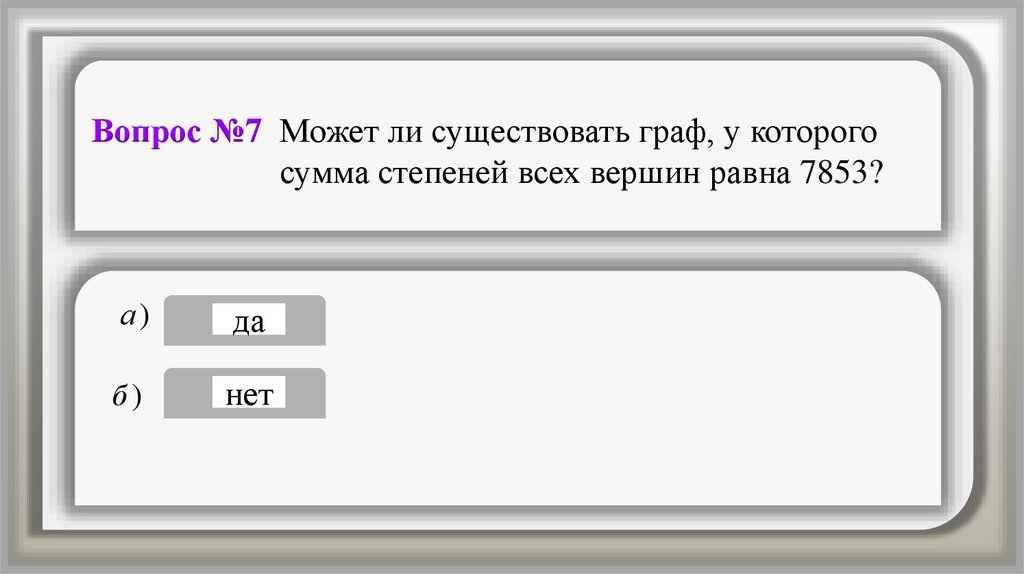
Вопрос №7 Может ли существовать граф, у которого
сумма степеней всех вершин равна 7853?
а)
да
б)
нет

53.

Ответы
на вопросы теста

54.

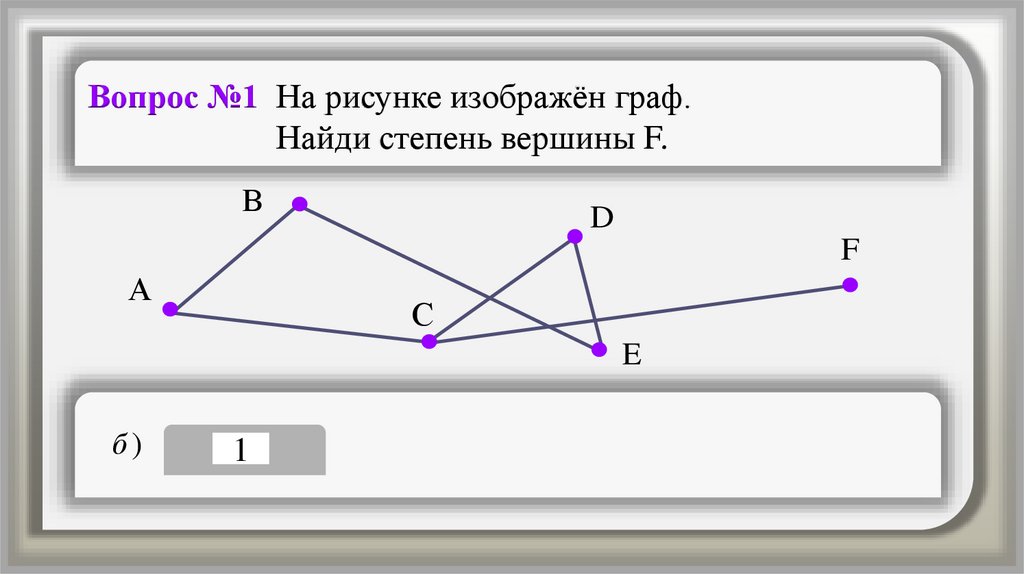
Вопрос №1 На рисунке изображён граф.
Найди степень вершины F.
В
D
F
А
С
E
б)
1

55.

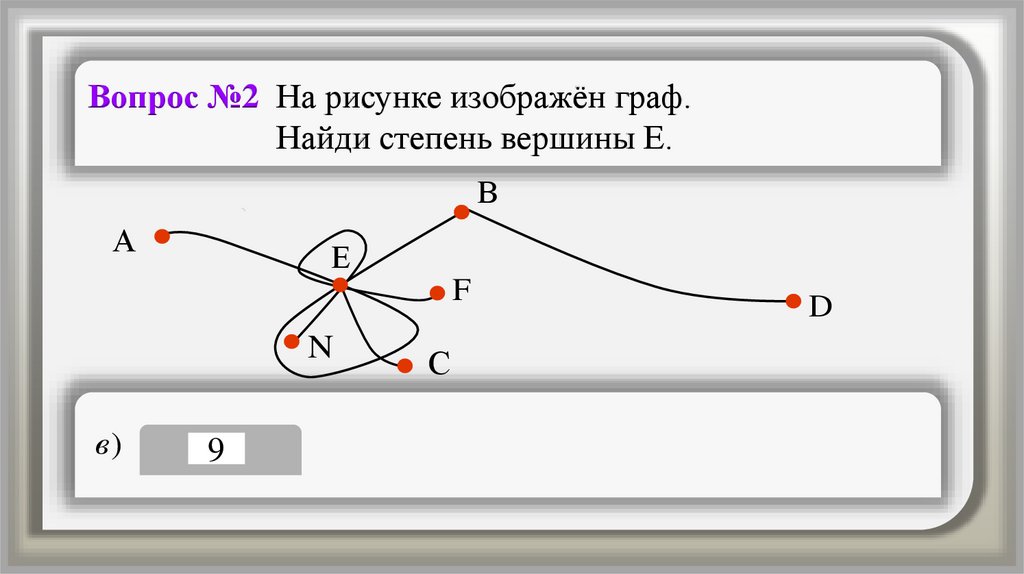
Вопрос №2 На рисунке изображён граф.
Найди степень вершины Е.
В
А
Е
F
N
в)
9
С
D

56.

Вопрос №3 Чтобы найти количество рёбер графа, надо:
а)
сумму степеней его вершин разделить пополам.

57.

Вопрос №4 В некотором графе 5 вершин, степени
которых равны: 2; 1; 14; 2; 11.
Сколько в этом графе рёбер?
б)
15

58.

Вопрос №5 В графе шесть вершин имеют
степень 5, четыре вершины − степень 6.
Сколько рёбер в этом графе?
б)
27

59.

Вопрос №6 В графе все степени вершин равны.
Вершин у него 26, а рёбер 78.
Чему равна степень любой вершины этого графа?
в)
6

60.

Вопрос №7 Может ли существовать граф, у которого
сумма степеней всех вершин равна 7853?
б)
нет

61.

Вопросы

62.

Что такое степень вершины графа?
Что такое петля в графе?
Каким числом является сумма
всех степеней графа?

63.

Спасибо
за внимание!