grafy

1.

Степень (валентность)
вершины.
Число рёбер и суммарная
степень вершин.
Путь в графе. Цепи и
циклы

2. Повторение

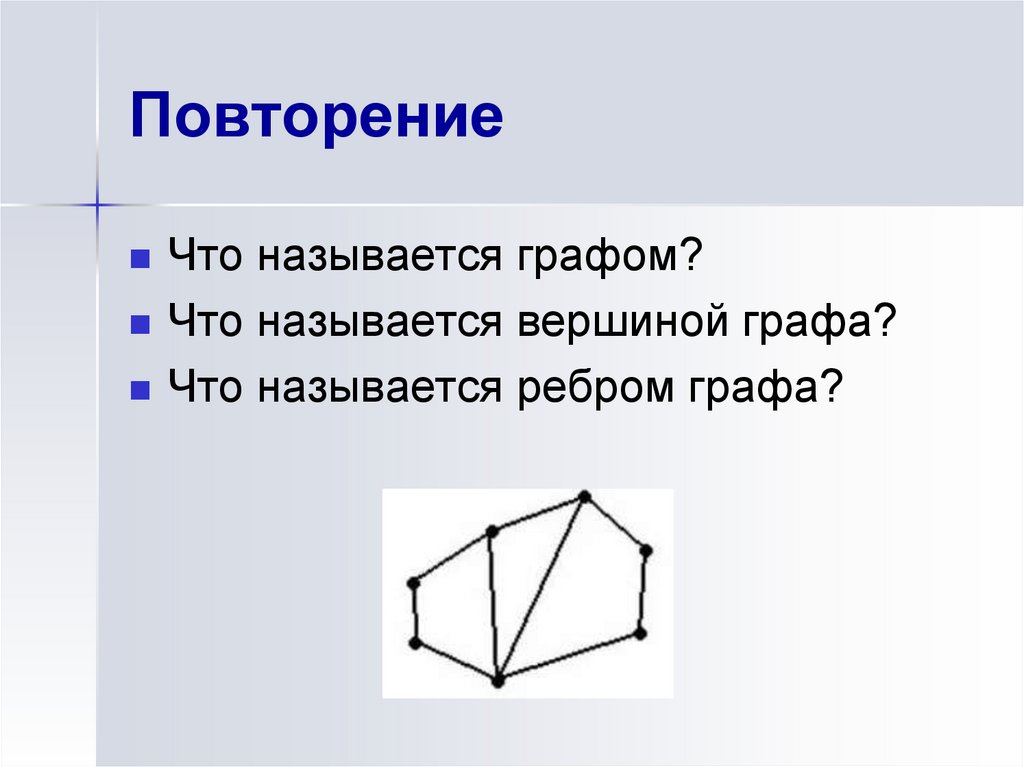
Что называется графом?
Что называется вершиной графа?
Что называется ребром графа?

3.

Степень (валентность)
вершины графа
Степень вершины в графе — это
количество ребер, которые из нее исходят.
Если ребро соединяет вершину с этой же
вершиной (ребро образует петлю), то такое
ребро считается дважды.
Иногда степень вершины
называют валентностью.

4.

На рисунке вершины A и B имеют
степень 2, вершина D имеет степень 0,
вершина C имеет степень 3. Степень
вершины E тоже равна 3, поскольку из
нее идет одно ребро к вершине C, а еще
одно ребро образует петлю: оба конца
этого ребра входят в вершину E.

5. Свойство степеней вершин

У каждого ребра в графе два конца.
Поэтому в любом графе сумма
степеней вершин в два раза
больше числа рёбер.

6.

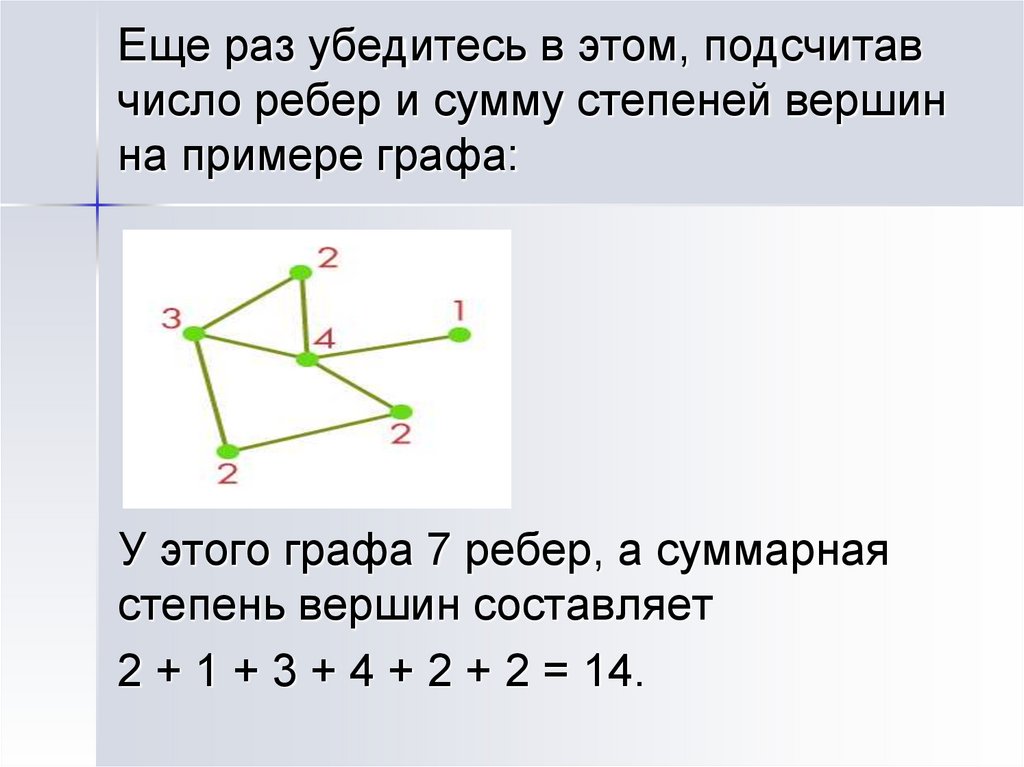
Еще раз убедитесь в этом, подсчитав
число ребер и сумму степеней вершин
на примере графа:
У этого графа 7 ребер, а суммарная
степень вершин составляет
2 + 1 + 3 + 4 + 2 + 2 = 14.

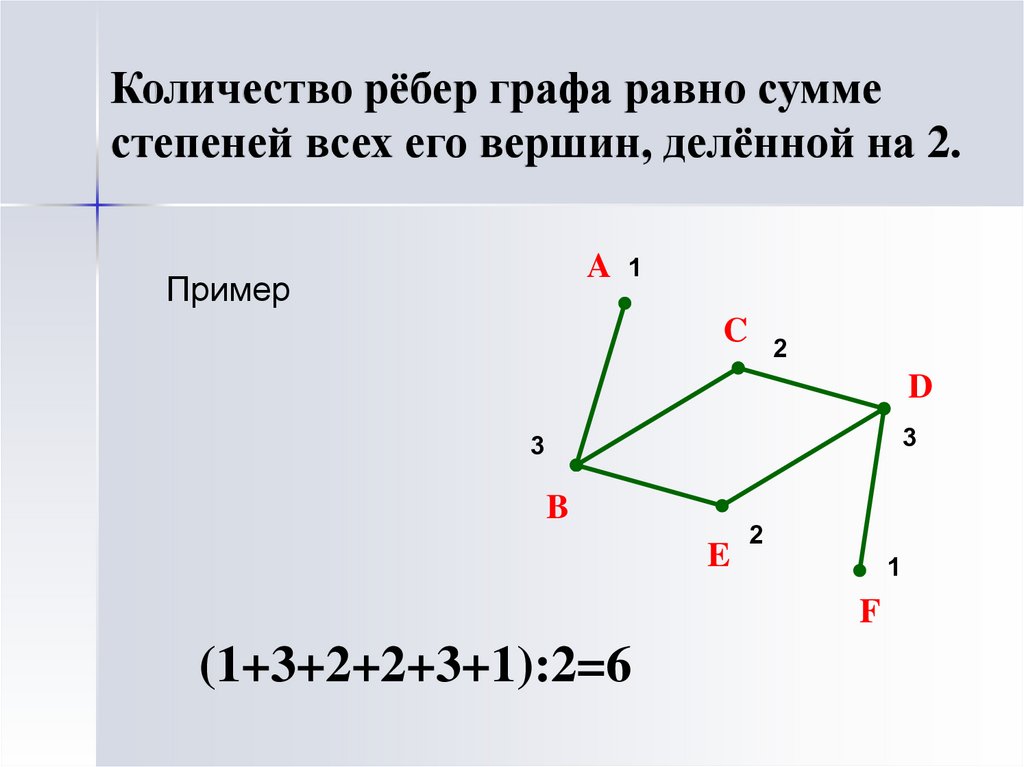
7. Количество рёбер графа равно сумме степеней всех его вершин, делённой на 2.

A 1
Пример
C
2
D
3
3
B
E
2
1
F
(1+3+2+2+3+1):2=6

8.

Подсчет числа ребер графа
Задача 1. В государстве 100 городов, из каждого
выходит 2 дороги, кроме столицы, откуда выходит
6 дорог. Сколько всего дорог в государстве?
Решение. Сложим количества дорог, выходящих из
всех городов (найдем сумму степеней):
99 ∙ 2 + 6 = 204.
Поскольку каждая дорога связывает два города, то
количество дорог будет вдвое меньше, а именно
102.
Ответ: 102 дороги.

9.

2. Может ли в государстве, в котором из
каждого города выходит ровно 3 дороги,
быть ровно 100 дорог?
Решение.
Пусть х – число городов.
Число дорог:
(3х)/2 или 100 дорог.
(3х)/2 = 100
3х=200
х = 200/3
Число городов может быть только натуральным,
значит 100 дорог в таком государстве быть не
может.
Ответ: не может.

10.

Теорема. Сумма степеней всех вершин
графа равна удвоенному числу ребер
этого графа.
2+3+3+2+2+3+3+2 = 12·2
24
=
24

11.

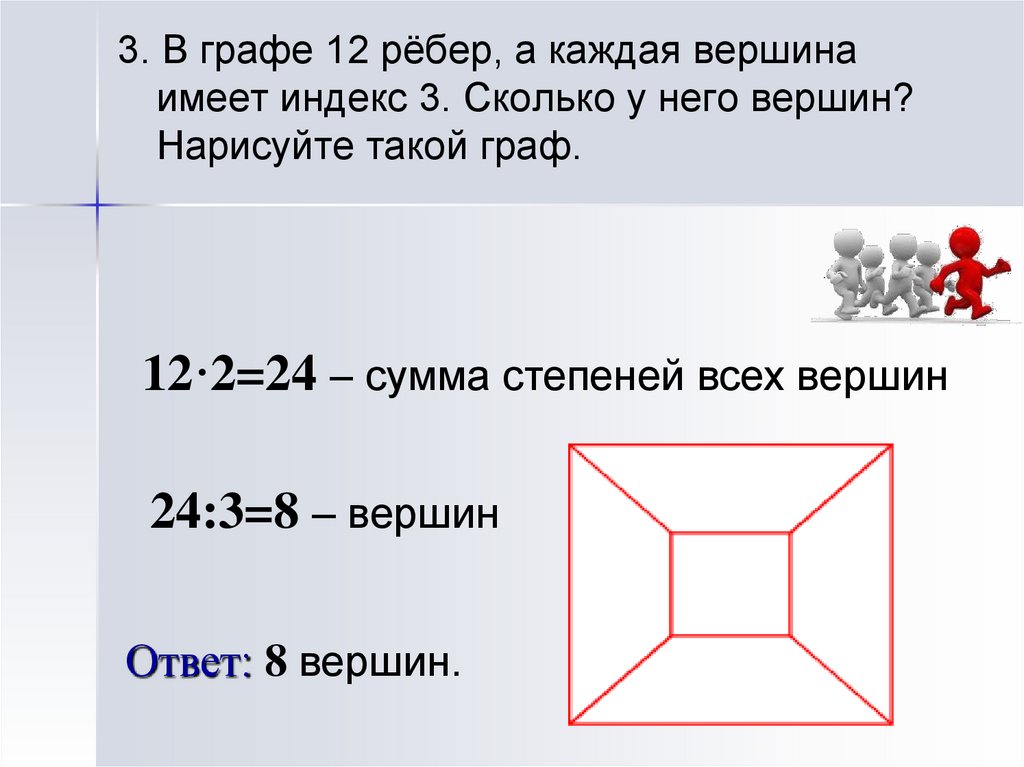
3. В графе 12 рёбер, а каждая вершина
имеет индекс 3. Сколько у него вершин?
Нарисуйте такой граф.
12·2=24 – сумма степеней всех вершин
24:3=8 – вершин
Ответ: 8 вершин.

12.

Следствие . Сумма степеней всех
вершин графа - четное число
4. В классе 15 компьютеров. Можно ли их
соединить друг с другом так, чтобы каждый
компьютер был соединен ровно с пятью
другими?
15·5=75 – сумма степеней всех вершин
Ответ: невозможно.

13.

Следствие . Число вершин с
нечетным индексом четно.
5. Может ли граф иметь пять вершин,
в каждой из которых сходится три ребра?
Ответ: Нет. Число вершин с нечетным индексом
должно быть четным.
6. В классе 30 человек. Может ли быть так,
что 9 человек имеют по 3 друга, 11 – по 4
друга, а 10 – по 5 друзей ?
Ответ: Нет. Число вершин с нечетным индексом должно
быть четным (9 человек – 3 друга).

14. Ориентированный граф

Граф называется ориентированным,
если указано направление (начало и
конец) каждого ребра.

15. Степень вершины ориентированного графа

Назовем число ребер, входящих в
вершину входящей степенью вершины.
Аналогично, число исходящих ребер
назовем исходящей степенью.

16. Свойство степеней вершин ориентированного графа

В ориентированном графе сумма
исходящих степеней всех вершин равна
сумме входящих степеней всех вершин
и равна числу ребер

17. Путь в графе

Путем в графе будем называть
последовательность ребер, по которой
можно «пройти» из одной вершины в
другую. Если в графе любые две
вершины соединены путем, то такой
граф называется связным.

18. Цепи и циклы

Путь в графе, у которого вершины не
повторяются, называется цепью. Цепью
также называется граф, у которого
вершины последовательно соединены
ребрами.

19.

Цепи и циклы
Иногда путь «идет по кругу». Говорят,
что такой путь образует цикл. Путь, у
которого первая и последняя вершины
совпадают, а промежуточные вершины
не повторяются, называется циклом.

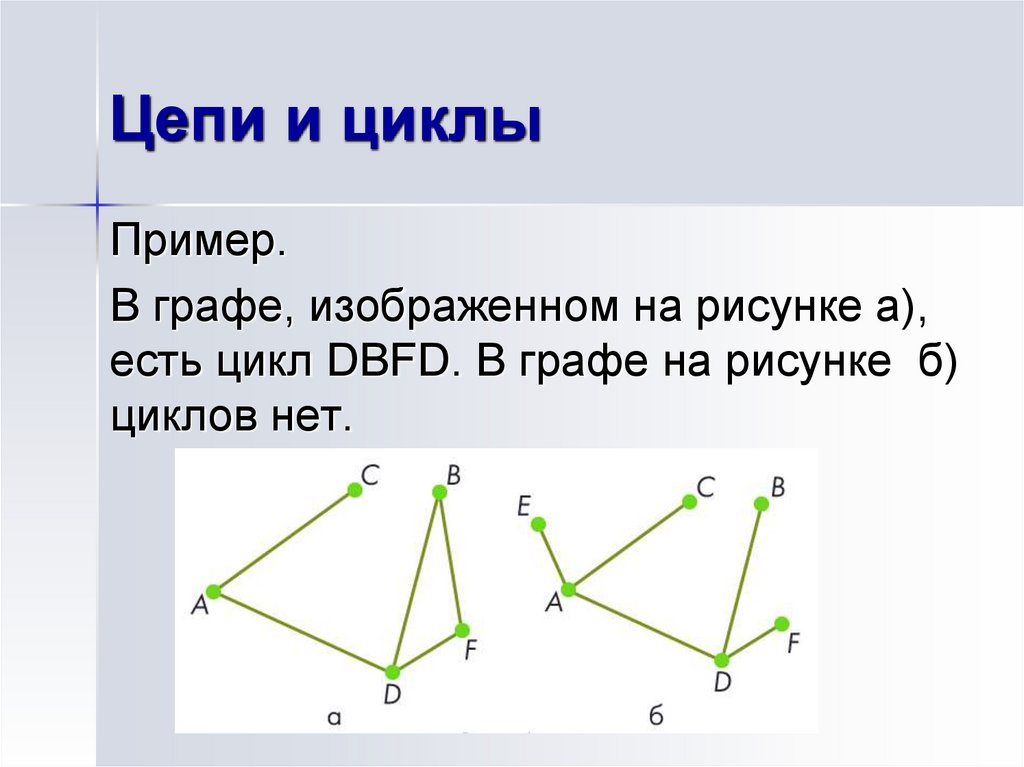
20. Цепи и циклы

Пример.
В графе, изображенном на рисунке а),
есть цикл DВFD. В графе на рисунке б)
циклов нет.

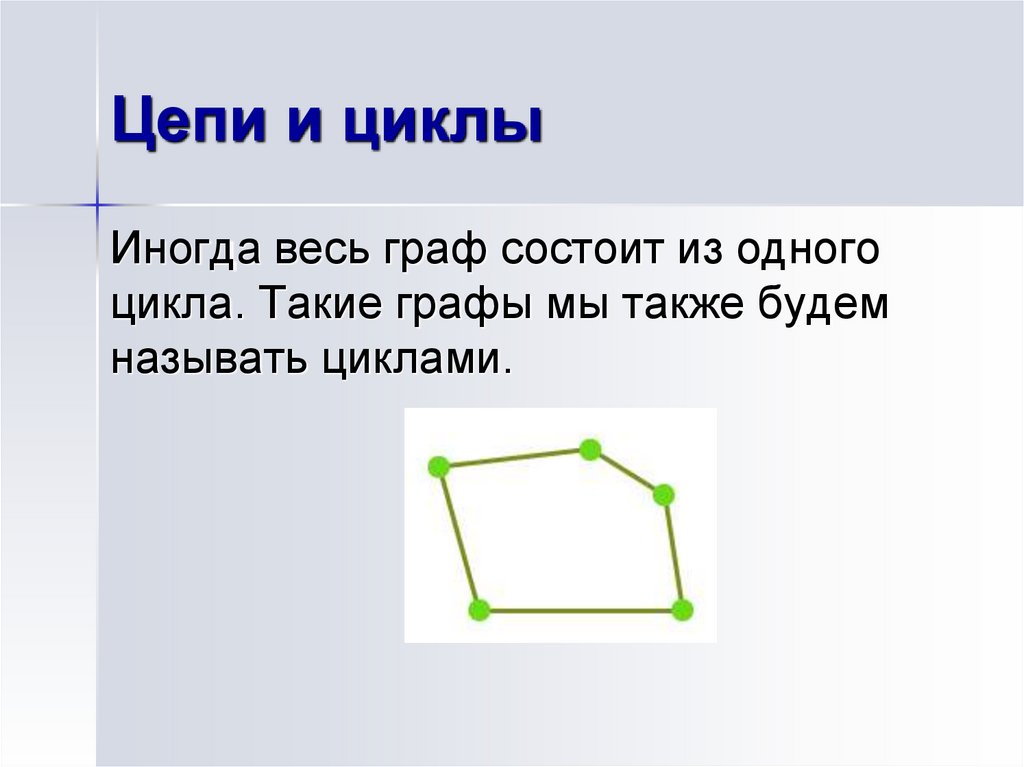
21. Цепи и циклы

Иногда весь граф состоит из одного
цикла. Такие графы мы также будем
называть циклами.

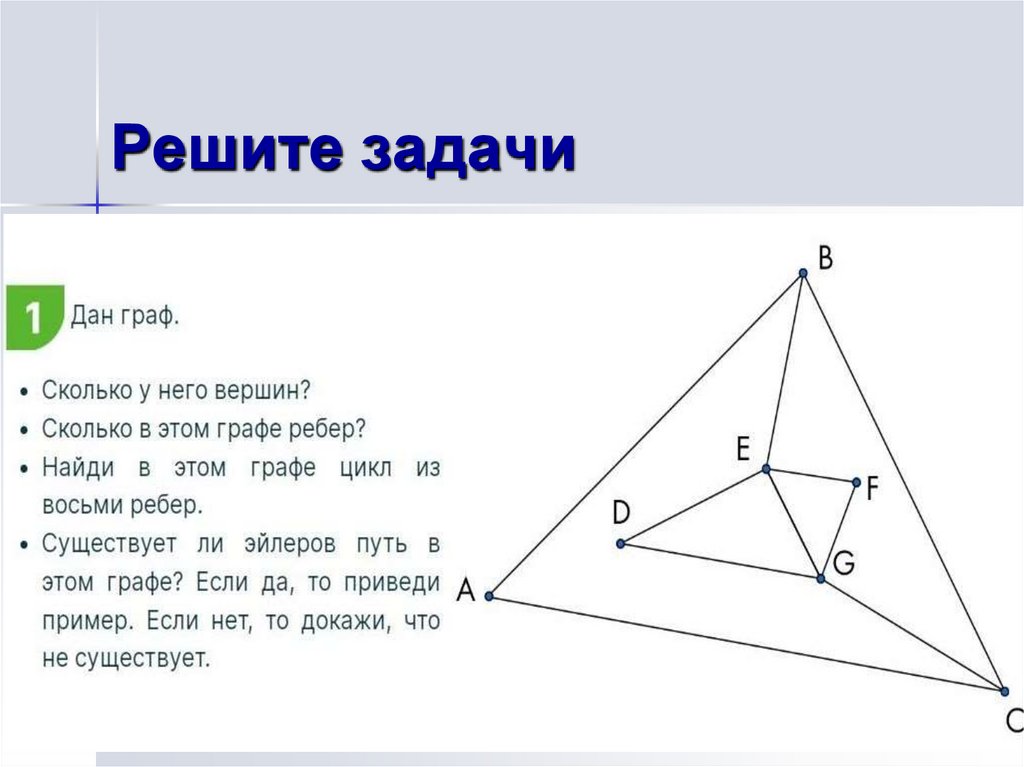
22. Решите задачи

23.

24. Домашнее задание

Изучите презентацию.
В тетради запишите число, тему урока,
сделайте краткий конспект презентации.
Письменно решите задачи 1 и 2.