Similar presentations:
Степень вершины. Путь в графе. Цепи и циклы
1.
Степень вершины.Путь в графе. Цепи и
циклы
2. Ориентированный граф
Граф называется ориентированным,если указано направление (начало и
конец) каждого ребра.
3. Степень вершины ориентированного графа
Назовем число ребер, входящих ввершину входящей степенью вершины.
Аналогично, число исходящих ребер
назовем исходящей степенью.
4. Свойство степеней вершин ориентированного графа
В ориентированном графе суммаисходящих степеней всех вершин равна
сумме входящих степеней всех вершин
и равна числу ребер
5. Путь в графе
Путем в графе будем называтьпоследовательность ребер, по которой
можно «пройти» из одной вершины в
другую. Если в графе любые две
вершины соединены путем, то такой
граф называется связным.
6. Цепи и циклы
Путь в графе, у которого вершины неповторяются, называется цепью. Цепью
также называется граф, у которого
вершины последовательно соединены
ребрами.
7.
Цепи и циклыИногда путь «идет по кругу». Говорят,
что такой путь образует цикл. Путь, у
которого первая и последняя вершины
совпадают, а промежуточные вершины
не повторяются, называется циклом.
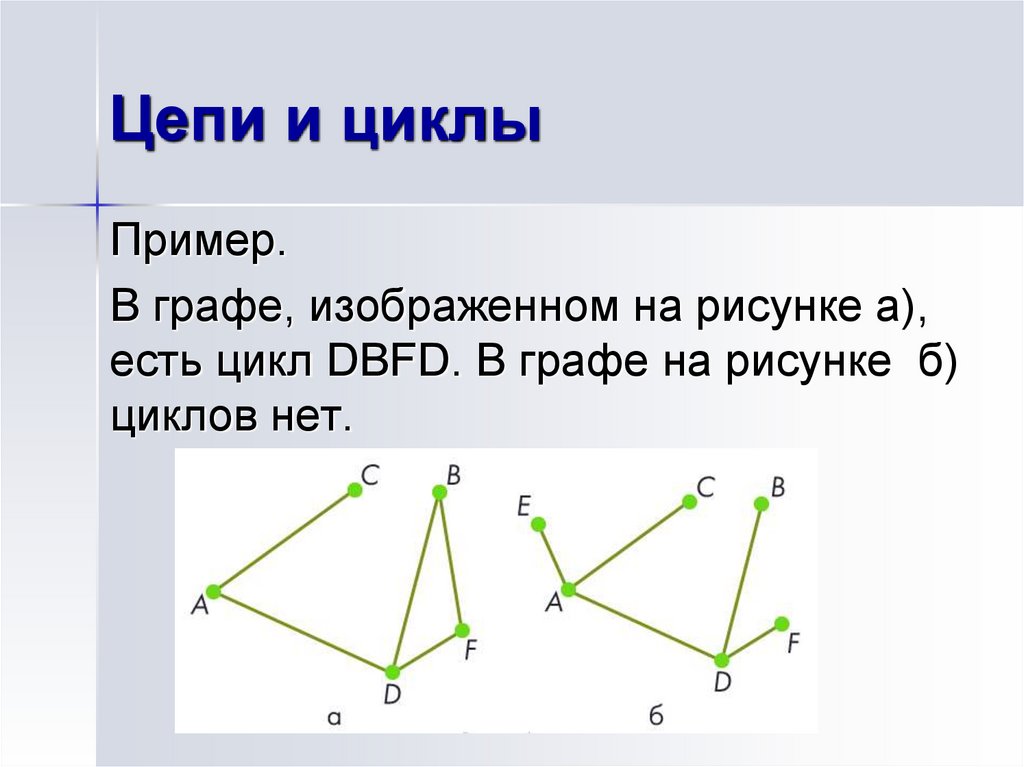
8. Цепи и циклы
Пример.В графе, изображенном на рисунке а),
есть цикл DВFD. В графе на рисунке б)
циклов нет.
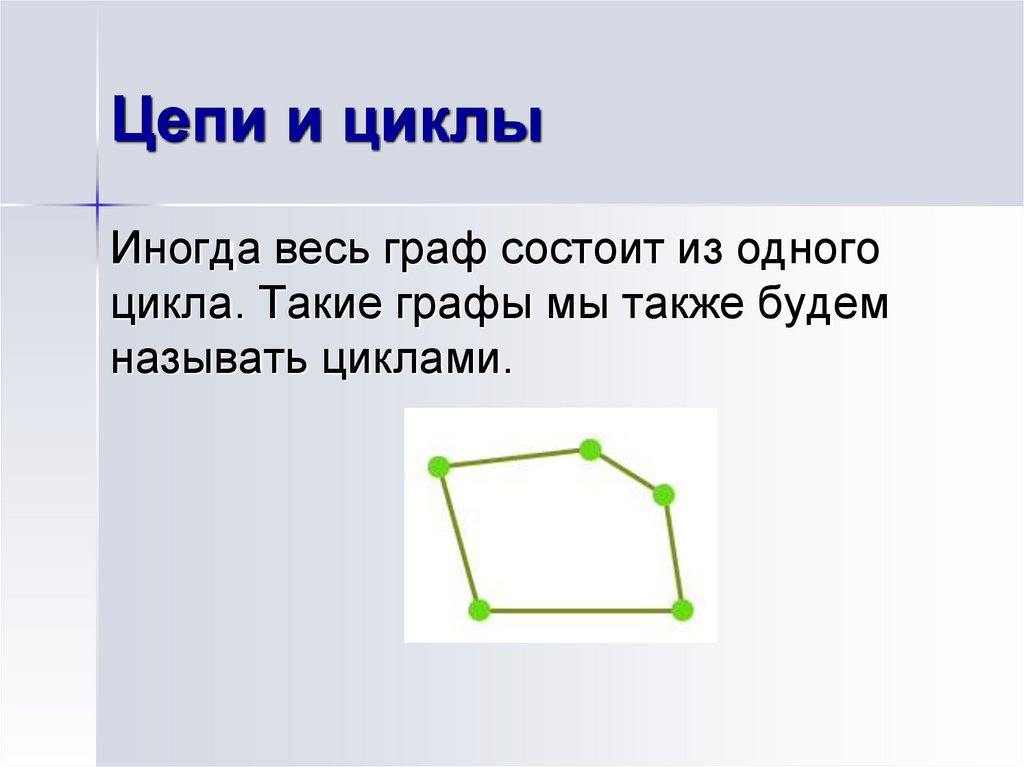
9. Цепи и циклы
Иногда весь граф состоит из одногоцикла. Такие графы мы также будем
называть циклами.
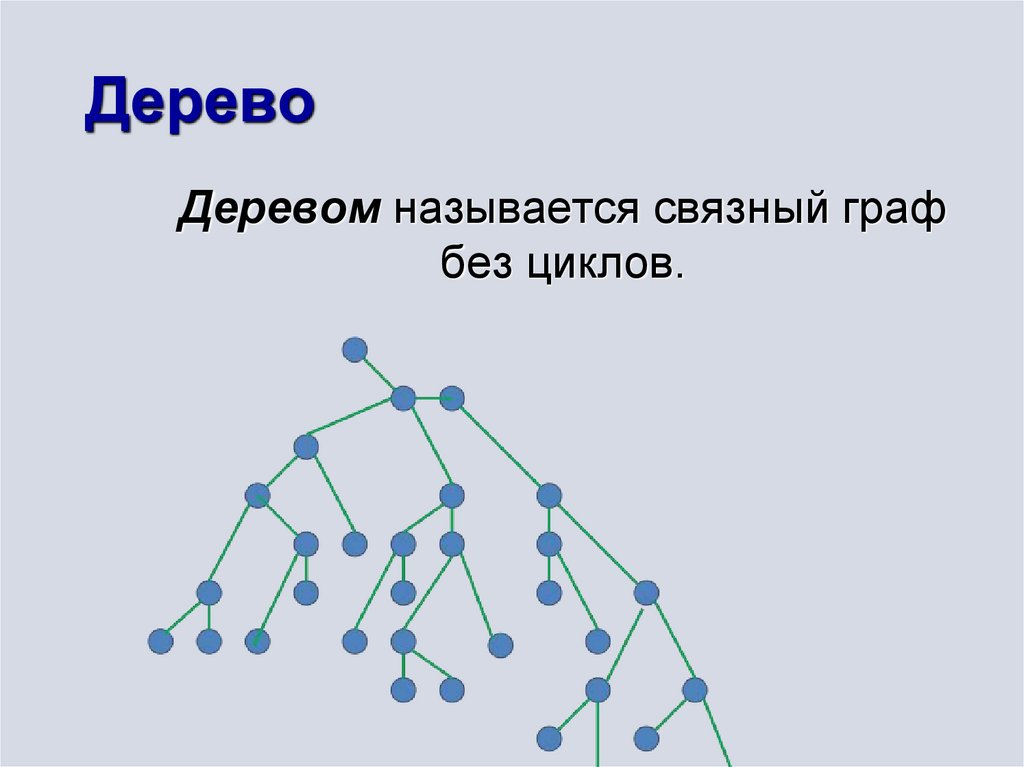
10. Дерево
Деревом называется связный графбез циклов.
11.
Свойство деревьевЛюбая пара вершин соединена
единственным маршрутом.
2.
Количество ребер меньше на одну
чем вершин.
3.
Удаление хотя бы одного ребра не
нарушает его структуру.
4.
если в дерево добавить хотя бы одно
ребро то появиться цикл.
1.
12.
Решите задачи№1 Аркадий, Борис, Владимир, Григорий и
Дмитрий
при
встрече
обменялись
рукопожатиями (каждый пожал руку каждому по
одному разу). Сколько всего рукопожатий было
сделано?
№ 2 В Изумрудном городе шесть площадей.
Каждая площадь соединена прямыми
улицами с тремя другими площадями.
Никакие две улицы не пересекаются.
Начертить возможный план такого города.
13. №3.
В первенстве класса по настольному теннисупринимали участие 5 учеников: Андрей, Борис, Галина,
Олег, Елена.
Первенство проводилось по круговой системе – каждый
участник играет с каждым из остальных один раз.
К настоящему моменту некоторые игры уже проведены:
Андрей сыграл с Борисом, Галиной и Еленой;
Борис с Андреем и Галиной;
Галина с Андреем и Олегом.
Сколько игр проведено к настоящему
моменту и сколько ещё осталось?
14.
№ 4 Ответьте на вопросы. Обоснуйте.1
2
3
1) 2,3,5,4 – маршрут?
2) 2,3,4,5,1,4,3- маршрут?
3) 3,1,4,5,1,2- путь?
4) 2,3,1,4,3,1,2 – цикл?
5) 2,3,1,4,5,1,2- цикл?
6) 2,3,4,5,1,2- цикл?
4
5











 mathematics
mathematics








