Обработка результатов прямых и косвенных измерений

1.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Уфимский государственный авиационный технический университет» (ФГБОУ ВО «УГАТУ»)
У ГАТ У
ЛАБОРАТОРНАЯ РАБОТА №2
«ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ»
Мезенцева Анастасия Ильфатовна, ст. преподаватель
Кафедра информационно-измерительной техники

2.

У ГАТ У
Уфимский государственный
авиационный технический
университет
ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
1. ЦЕЛЬ РАБОТЫ
Изучение вероятностных методов оценки погрешности результатов измерений и
определение результата измерения и показаний точности прямых и косвенных
измерений.
2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
При проведении с одинаковой тщательностью и в одинаковых условиях
повторных измерений одной и той же постоянной величины получаются результаты
измерений (наблюдений), как отличающиеся друг от друга, так и совпадающие. Такие
расхождения в результатах измерений говорят о наличии в них случайных
погрешностей. Каждая случайная погрешность возникает при одновременном
воздействии многих источников. Каждый из этих источников сам по себе оказывает
незаметное влияние на результат измерения, но суммарное воздействие всех
источников может оказаться достаточно сильным. Случайные погрешности можно
оценить методами математической статистики с привлечением теории
вероятности при многократных измерениях одной и той же величины.
2
2

3.

У ГАТ У
Уфимский государственный
авиационный технический
университет
Для оценки точности результатов измерений, содержащих случайные
погрешности, существует несколько способов. Наиболее распространена оценка
точности в виде среднего квадратического отклонения результата наблюдений, под
которым понимают параметр функции распределения результатов наблюдений,
характеризующий их рассеивание и равный корню квадратному из дисперсии
результата наблюдений с положительным знаком. Для нахождения среднего
квадратического отклонения необходимо знать закон распределения случайной
погрешности. В практике электрических измерений встречаются различные законы
распределения. Если соблюдены условия возможности применения центральной
предельной теоремы вероятностей, можно считать, что закон распределения
суммарной случайной погрешности нормальный.
Нормальный закон (Гаусса) базируется на двух аксиомах:
- при очень большом числе измерений случайные погрешности, равные по
величине, но различные по знаку, встречаются одинаково часто;
- чаще всего встречаются меньшие погрешности, а большие погрешности
встречаются тем реже, чем они больше.
3
ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ

4.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
Математически нормальное распределение случайных погрешностей может быть
представлено формулой:
x2
1
2
e 2 ,
(2.1)
f ( x)
2
где f(Δx) - плотность вероятности случайной погрешности x ;
σ - среднее квадратическое отклонение.
Согласно теории вероятностей, среднее квадратическое отклонение случайной
погрешности ряда измерений может быть приближенно выражено в виде:
_
2
(xi x)
n
i 1
.
(2.2)
n 1
Если х1, х2, …, хn - совокупность измеренных значений величины x, то за оценку
результата измерения принимают среднее арифметическое значение:
_ 1 n
(2.3)
x xi .
n i 1
В качестве оценки среднего квадратического отклонения результата измерения
принимают:
4

5.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
_
S(x)
_
2
(xi x)
n
i 1
n(n 1)
.
(2.4)
При проведении измерений стремятся получить результат измерения с
погрешностью, не превышающей допускаемое значение. Знание только среднего
квадратического отклонения не позволяет найти максимальную погрешность,
которая может встретиться при измерениях, что свидетельствует об ограниченных
возможностях этой числовой характеристики.
Максимальные значения погрешности зависят не только от среднего
квадратического отклонения, но и от вида закона распределения. Когда
распределение погрешности теоретически неограниченно, например, при
нормальном законе распределения, погрешность может быть любой по значению. В
этом случае можно лишь говорить об интервале, за границы которого погрешность
не выйдет с некоторой вероятностью. Этот интервал называют доверительным
интервалом, характеризующую его вероятность – доверительной вероятностью, а
границы этого интервала – доверительными значениями погрешности
(доверительными границами).
5

6.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
Доверительные границы (без учета знака) случайной составляющей
погрешности результата измерения находят по формуле
_
tn S(x),
(2.5)
где
tn - коэффициент Стьюдента, зависящий от числа измерений n и
доверительной вероятности P .
д
Для определения доверительных границ погрешности результата измерения
доверительную вероятность в соответствии с ГОСТ 8.207-76 принимают равной
0,95. В тех случаях, когда измерение нельзя повторить или результаты измерений
имеют значение для здоровья людей, помимо границ, соответствующих Sa , Sb , Sc
указывают границы для доверительной вероятности 0,99 и выше.
При косвенных измерениях результат y находится по известной
функциональной зависимости между измеряемой величиной y и величинами a, b, c,
…, которые могут быть определены прямыми измерениями.
Погрешности косвенных измерений величины y зависят от погрешностей
прямых измерений величин a, b, c.
6

7.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
Для оценки результатов косвенных измерений величины y будем считать, что
систематические погрешности измерений величин a, b, c исключены, а случайные
погрешности измерения этих величин не зависят друг от друга, т.е. не
коррелированны.
___
Для вычисления среднего квадратического отклонения результата y измеряемой
величины y используют средние квадратические отклонения, полученные при
прямых измерениях величин a, b, c.
В общем виде при нелинейной зависимости между y и a, b, c отклонение
результатов косвенного измерения S y определяется как
S y Da2 Db2 D 2c ,
где Da, Db, Dс - частные погрешности косвенного измерения, равные
7
(2.6)

8.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
dy
dy
dy
(2.7)
S a ; Db S b ; Dc S c ,
da
db
dc
где Sa, Sb, Sс - средние квадратические отклонения результатов прямых измерений
величин a, b, c.
Da
Погрешность результата косвенных измерений в доверительных границах при
заданной доверительной вероятности Pд определяется как
dy
dy
dy
y a b c ,
db dc
da
где a tn S (a); b tn S (b); c tn S (c).
2
8
2
2
(2.8)

9.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
3. ЗАДАНИЕ
3.1. Отчет по лабораторной работе оформляется в электронном виде и должен быть сохранен в формате .docx
или .pdf под именем вида: ЛРN-n-Ф.И.О.docx(pdf), где N – номер лабораторной работы, n – номер варианта.
Отчет должен содержать следующие элементы: номер и название лабораторной работы, теоретическую часть,
практическую (расчетную) часть, выводы по работе.
Теоретическая часть должна содержать ответы на контрольные вопросы, приведенные в конце
лабораторной работы.
Практическая (расчетная) часть должны быть оформлена в соответствии с п.4 и содержать все
необходимые рисунки, расчетные формулы и пояснения.
Вывод по лабораторной работе должен отражать ответ и объяснение ответа на вопрос пункта 3.6.
3.2. Изучить вероятностные методы обработки результатов прямых и косвенных измерений.
3.3. По варианту (приведенные в конце лабораторной работы) провести обработку результатов 10 прямых
измерений активного сопротивления резистора, полученных с помощью цифрового омметра (п.п. 4.1. п 4).
3.4. Изучить схему для измерения активного сопротивления резистора порядка 100÷300 Ом на постоянном токе
косвенным методом (п.п. 4.2. п 4).
3.5. По варианту (приведенные в конце лабораторной работы) провести обработку однократного измерения тока,
обработку результатов 10 прямых измерений напряжения. Найти результат косвенного измерения сопротивления,
показатели точности и достоверности результата измерения (п.п. 4.2. п 4).
3.6. Сравнить результаты прямых и косвенных измерений сопротивления.
9

10.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
4. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ
И ОБРАБОТКИ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
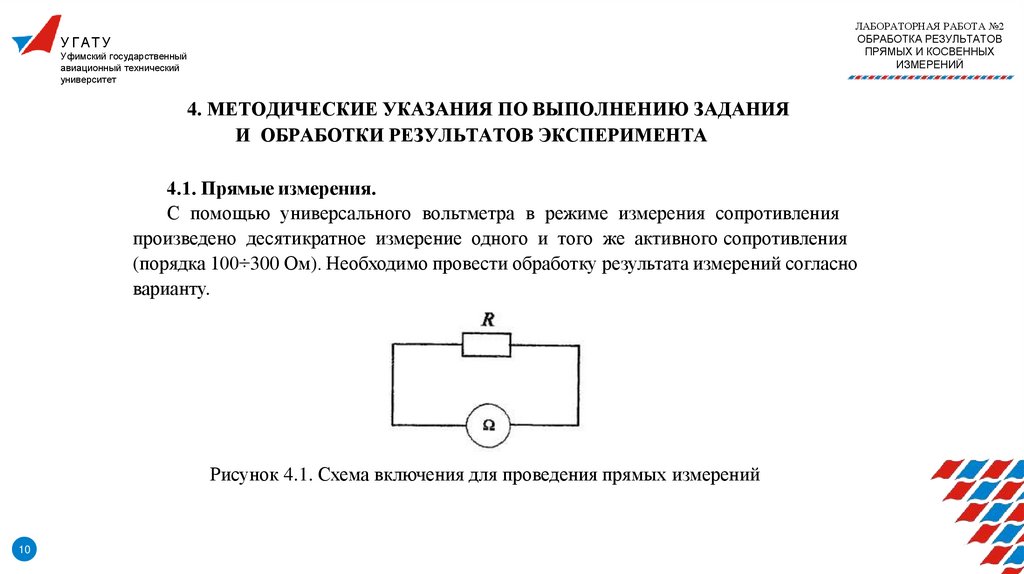
4.1. Прямые измерения.
С помощью универсального вольтметра в режиме измерения сопротивления
произведено десятикратное измерение одного и того же активного сопротивления
(порядка 100÷300 Ом). Необходимо провести обработку результата измерений согласно
варианту.
Рисунок 4.1. Схема включения для проведения прямых измерений
10

11.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
Обработку результатов измерений активного сопротивления производят в
следующей последовательности:
а) находят среднее арифметическое значение результатов измерений по формуле
1 n
(4.1)
R Ri ,
n i 1
которое принимают за результат измерения;
б) вычисляют отклонения от среднего арифметического результата
(4.2)
1 R1 R, 2 R2 R, ..., n Rn R;
в) проверяют правильность вычислений и, если они верны, то должно быть
n
i 0;
(4.3)
i 1
г) вычисляют квадраты отклонений от среднего арифметического результата
n
, , ..., и их сумму i2 .
2
1
2
2
2
n
i 1
Данные измерений и вычислений вносятся в таблицу 4.1.
11

12.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
Таблица 4.1. Обработка результатов прямых измерений сопротивления
n
1.
2.
3.
4.
5.
6.
7.
8.
9.
10
Ri, Ом
n
R
12
2
ρi, Ом
i
i 1
ρi , Ом
n
i2
i 1
2

13.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
д) определяют оценку среднего квадратического отклонения ряда измерений
n
Ri R
i 1
2
;
n 1
е) вычисляют оценку среднего квадратического
измерения
S( R )
;
(4.4)
отклонения результата
(4.5)
n
ж) определяют доверительные границы случайной составляющей погрешности
результата измерения
tn S(R).
(4.6)
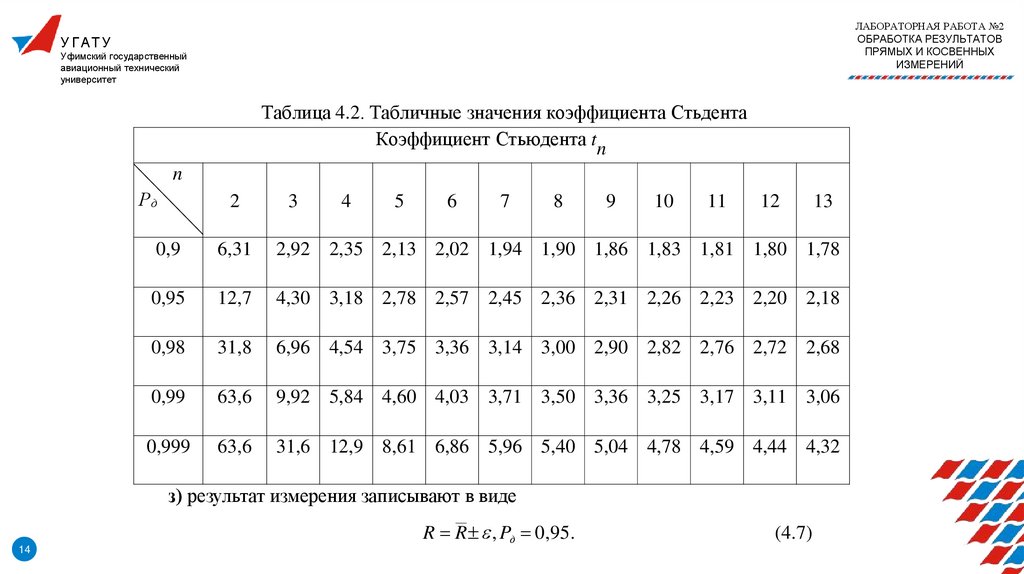
Коэффициент Стьюдента tn находят из таблицы 4.2 для доверительной
вероятности Рд=0,95 и числе измерений n=10.
13

14.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
Таблица 4.2. Табличные значения коэффициента Стьдента
Коэффициент Стьюдента tn
n
Рд
2
3
4
5
6
7
8
9
10
11
12
0,9
6,31
2,92 2,35 2,13 2,02 1,94 1,90 1,86 1,83 1,81 1,80 1,78
0,95
12,7
4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 2,23 2,20 2,18
0,98
31,8
6,96 4,54 3,75 3,36 3,14 3,00 2,90 2,82 2,76 2,72 2,68
0,99
63,6
9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06
0,999
63,6
31,6 12,9 8,61 6,86 5,96 5,40 5,04 4,78 4,59 4,44 4,32
з) результат измерения записывают в виде
R R , Pд 0,95.
14
(4.7)
13

15.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
4.2. Косвенные измерения активного сопротивления.
По схеме измерения активного сопротивления резистора на постоянном токе
(того же значения, что и в п. 4.1) проведено 10 измерений напряжения и однократное
измерение тока. Обработать результаты измерения напряжения аналогично п. 4.1.
Рисунок 2.2. Схема включения для проведения косвенных измерений
Данные измерений занести в таблицу 4.3, куда также внести результаты вычислений.
15

16.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
Таблица 4.3. Обработка результатов прямых измерений напряжения
Ui, В
n
1.
2.
3.
4.
5.
6.
7.
8.
9.
10
n
U
16
2
2
ρi , В
ρi, В
i
i 1
n
i2
i 1

17.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
Обработать результаты прямых измерений напряжения по методике, описанной
в п.4.1 и записать результат измерения в виде:
U U U , Pд 0,95 .
(4.8)
Результат однократного измерения тока принимаем равным I = … мА
(по варианту). Результат однократного измерения тока I прибором оценивается
энтропийной погрешностью равной
I K э S ( I ) ,
где KЭ - энтропийный коэффициент, зависящий от закона распределения
погрешностей прибора и для нормального закона распределения равен 2,066, что
соответствует доверительной вероятности Рд=0,95.
17

18.

ЛАБОРАТОРНАЯ РАБОТА №2
ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ И КОСВЕННЫХ
ИЗМЕРЕНИЙ
У ГАТ У
Уфимский государственный
авиационный технический
университет
Так как среднее квадратическое отклонение результата измерений S ( I ) при
однократном измерении не может быть определено, то абсолютная погрешность
измерения тока I с вероятностью Рд=0,95 может быть найдена исходя из класса
точности и предела измерения прибора
I
Im ,
(4.9)
100
где γ - класс точности, равный 0,5%;
Im - предел измерения прибора, 100 мА.
Результат измерения тока I записать в виде:
I I I , Pд 0,95,
(4.10)
где I - однократное значение тока, измеренное амперметром.
Результат косвенного измерения сопротивления представить в виде:
R R R, Pд 0,95,
(4.11)
где R - значение сопротивления, вычисленное по значениям U и I согласно формуле.
R dR U dR I 1 U U I .
2
dU
dI
I
I
2
18
2
2
2
(4.12)

19.

5. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие измерения называют прямыми? Косвенными?
2. В чем состоит отличие косвенных измерений от прямых?
3. В чем заключается сущность вероятностных методов точности результата измерений?
4. Дайте определение систематической и случайной погрешностей?
5. В каком виде записывается результат измерений?
6. Как влияет точность измерительных приборов на нахождение достоверного значения
измеряемой величины?
7. Дайте определение среднеквадратического отклонения результата наблюдений.
8. Дайте понятие доверительного интервала и доверительной вероятности.
9. Как определяется коэффициент Стьюдента?

20.

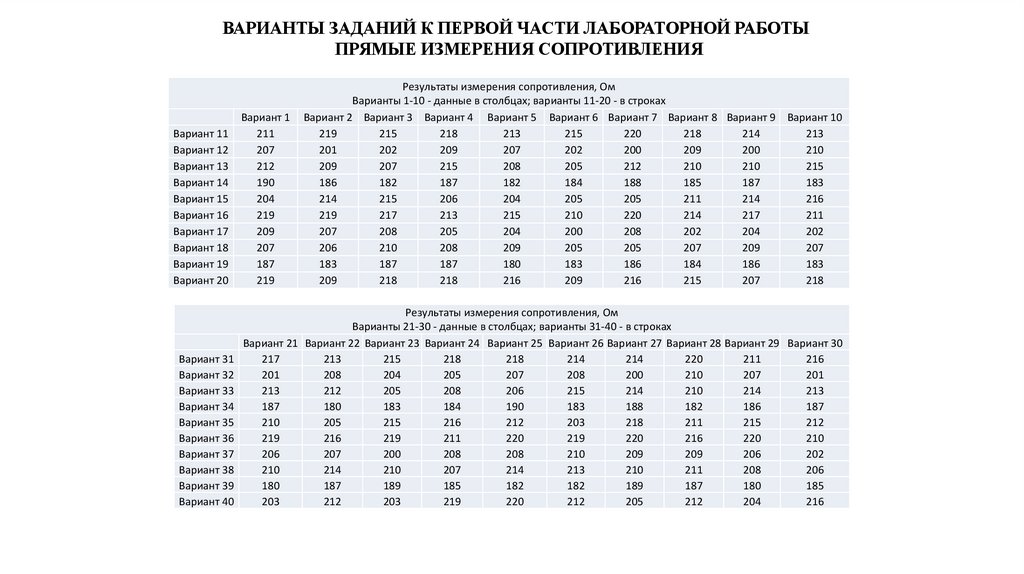
ВАРИАНТЫ ЗАДАНИЙ К ПЕРВОЙ ЧАСТИ ЛАБОРАТОРНОЙ РАБОТЫ
ПРЯМЫЕ ИЗМЕРЕНИЯ СОПРОТИВЛЕНИЯ
Результаты измерения сопротивления, Ом
Варианты 1-10 - данные в столбцах; варианты 11-20 - в строках
Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6 Вариант 7 Вариант 8 Вариант 9 Вариант 10
219
215
218
213
215
220
218
214
213
201
202
209
207
202
200
209
200
210
209
207
215
208
205
212
210
210
215
186
182
187
182
184
188
185
187
183
214
215
206
204
205
205
211
214
216
219
217
213
215
210
220
214
217
211
207
208
205
204
200
208
202
204
202
206
210
208
209
205
205
207
209
207
183
187
187
180
183
186
184
186
183
209
218
218
216
209
216
215
207
218
Вариант 11
Вариант 12
Вариант 13
Вариант 14
Вариант 15
Вариант 16
Вариант 17
Вариант 18
Вариант 19
Вариант 20
Вариант 1
211
207
212
190
204
219
209
207
187
219
Вариант 31
Вариант 32
Вариант 33
Вариант 34
Вариант 35
Вариант 36
Вариант 37
Вариант 38
Вариант 39
Вариант 40
Результаты измерения сопротивления, Ом
Варианты 21-30 - данные в столбцах; варианты 31-40 - в строках
Вариант 21 Вариант 22 Вариант 23 Вариант 24 Вариант 25 Вариант 26 Вариант 27 Вариант 28 Вариант 29 Вариант 30
217
213
215
218
218
214
214
220
211
216
201
208
204
205
207
208
200
210
207
201
213
212
205
208
206
215
214
210
214
213
187
180
183
184
190
183
188
182
186
187
210
205
215
216
212
203
218
211
215
212
219
216
219
211
220
219
220
216
220
210
206
207
200
208
208
210
209
209
206
202
210
214
210
207
214
213
210
211
208
206
180
187
189
185
182
182
189
187
180
185
203
212
203
219
220
212
205
212
204
216

21.

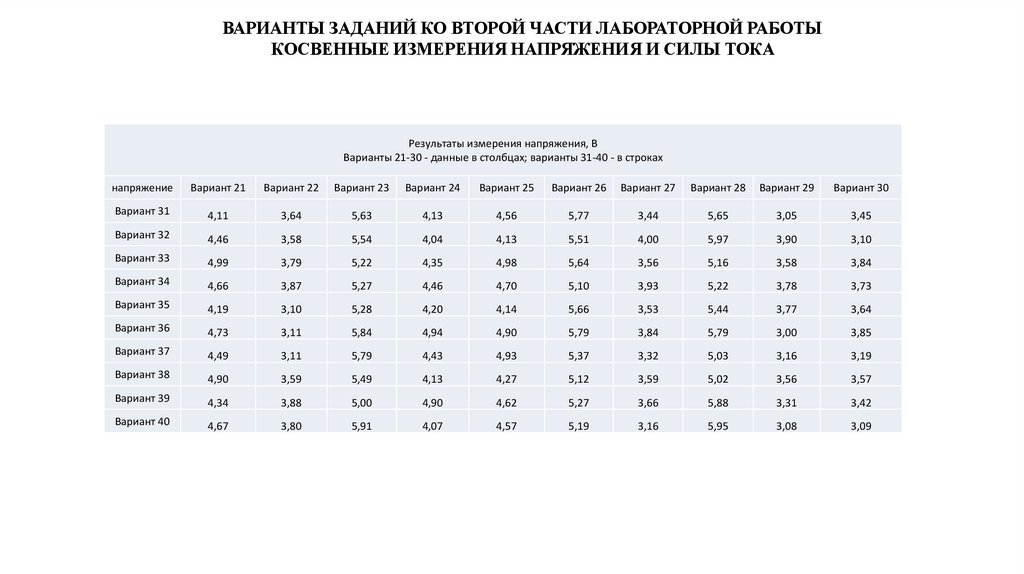
ВАРИАНТЫ ЗАДАНИЙ КО ВТОРОЙ ЧАСТИ ЛАБОРАТОРНОЙ РАБОТЫ
КОСВЕННЫЕ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И СИЛЫ ТОКА
Напряжение Вариант 1
Вариант 2
Результаты измерения напряжения, В
Варианты 1-10 - данные в столбцах; варианты 11-20 - в строках
Вариант 3 Вариант 4 Вариант 5 Вариант 6 Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 11
2,49
2,07
3,25
2,50
2,73
3,10
4,89
2,02
2,41
3,37
Вариант 12
2,05
2,36
3,12
2,84
2,79
3,47
4,78
2,86
2,62
3,14
Вариант 13
2,90
2,40
3,33
2,42
2,15
3,82
4,86
2,29
2,55
3,27
Вариант 14
2,07
2,58
3,52
2,82
2,99
3,14
4,20
2,05
2,00
3,67
Вариант 15
2,43
2,57
3,85
2,40
2,33
3,75
4,09
2,60
2,35
3,94
Вариант 16
2,36
2,30
3,56
2,81
2,94
3,08
4,09
2,80
2,08
3,14
Вариант 17
2,64
2,26
3,93
2,91
2,40
3,09
4,11
2,92
2,66
3,65
Вариант 18
2,57
2,32
3,82
2,78
2,54
3,75
4,85
2,40
2,84
3,40
Вариант 19
2,13
2,57
3,02
2,83
2,81
3,81
4,12
2,66
2,31
3,08
Вариант 20
2,98
2,48
3,24
2,02
2,66
3,86
4,57
2,33
2,65
3,73

22.

ВАРИАНТЫ ЗАДАНИЙ КО ВТОРОЙ ЧАСТИ ЛАБОРАТОРНОЙ РАБОТЫ
КОСВЕННЫЕ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И СИЛЫ ТОКА
Результаты измерения напряжения, В
Варианты 21-30 - данные в столбцах; варианты 31-40 - в строках
напряжение
Вариант 21
Вариант 22
Вариант 23
Вариант 24
Вариант 25
Вариант 26
Вариант 27
Вариант 28
Вариант 29
Вариант 30
Вариант 31
4,11
3,64
5,63
4,13
4,56
5,77
3,44
5,65
3,05
3,45
Вариант 32
4,46
3,58
5,54
4,04
4,13
5,51
4,00
5,97
3,90
3,10
Вариант 33
4,99
3,79
5,22
4,35
4,98
5,64
3,56
5,16
3,58
3,84
Вариант 34
4,66
3,87
5,27
4,46
4,70
5,10
3,93
5,22
3,78
3,73
Вариант 35
4,19
3,10
5,28
4,20
4,14
5,66
3,53
5,44
3,77
3,64
Вариант 36
4,73
3,11
5,84
4,94
4,90
5,79
3,84
5,79
3,00
3,85
Вариант 37
4,49
3,11
5,79
4,43
4,93
5,37
3,32
5,03
3,16
3,19
Вариант 38
4,90
3,59
5,49
4,13
4,27
5,12
3,59
5,02
3,56
3,57
Вариант 39
4,34
3,88
5,00
4,90
4,62
5,27
3,66
5,88
3,31
3,42
Вариант 40
4,67
3,80
5,91
4,07
4,57
5,19
3,16
5,95
3,08
3,09

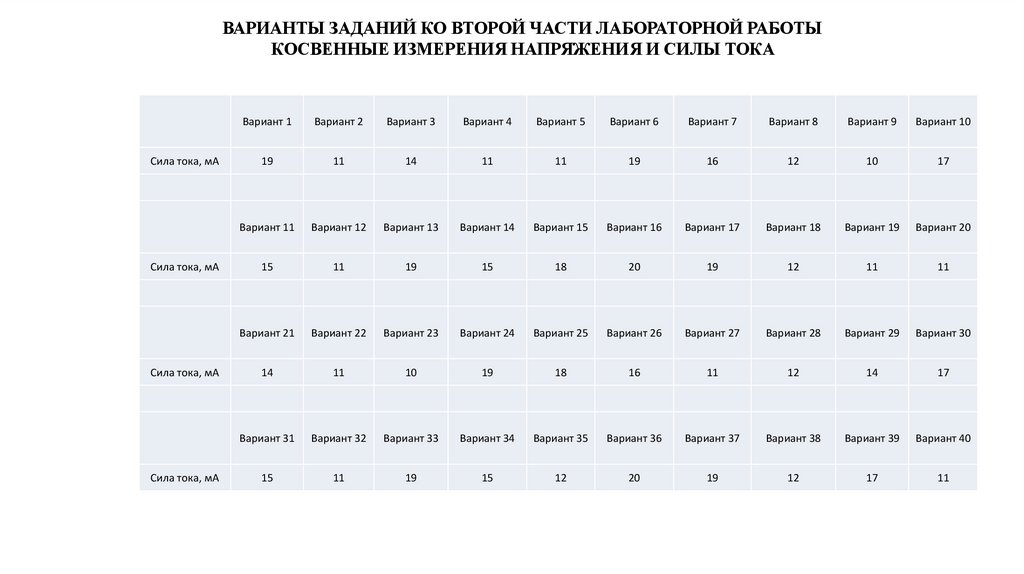
23.

ВАРИАНТЫ ЗАДАНИЙ КО ВТОРОЙ ЧАСТИ ЛАБОРАТОРНОЙ РАБОТЫ
КОСВЕННЫЕ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И СИЛЫ ТОКА
Сила тока, мА
Сила тока, мА
Сила тока, мА
Сила тока, мА
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
19
11
14
11
11
19
16
12
10
17
Вариант 11
Вариант 12
Вариант 13
Вариант 14
Вариант 15
Вариант 16
Вариант 17
Вариант 18
Вариант 19
Вариант 20
15
11
19
15
18
20
19
12
11
11
Вариант 21
Вариант 22
Вариант 23
Вариант 24
Вариант 25
Вариант 26
Вариант 27
Вариант 28
Вариант 29
Вариант 30
14
11
10
19
18
16
11
12
14
17
Вариант 31
Вариант 32
Вариант 33
Вариант 34
Вариант 35
Вариант 36
Вариант 37
Вариант 38
Вариант 39
Вариант 40
15
11
19
15
12
20
19
12
17
11