Случайные погрешности результатов измерений. Обработка результатов измерений (продолжение)

1.

Случайные погрешности результатов измерений
Обработка результатов измерений
(продолжение)

2.

Для
независимых
прямых
равноточных
измерений,
подчиненных
центрированному симметричному закону распределения вероятности,
среднее арифметическое является состоятельной, несмещенной и
эффективной оценкой истинного значения измеряемой величины.
1 n
x xi
n i 1

3.

Для нормального закона распределения оценку СКО отдельных
результатов измерений в серии из n независимых равноточных измерений
вычисляют по формуле:
n
1
2
S
(
x
x
)
i
(n 1) i 1
S- средняя квадратическая погрешность (СКП)
результатов единичных показаний в ряду измерений
σ^ x

4.

S
SQ
n
x
^
x
^
n
СКП среднего арифметического в n раз меньше, чем СКП результата
единичного измерения.
При этом если результаты единичного измерения подчиняются
нормальному закону распределения вероятности, то и среднее
арифметическое подчиняется нормальному закону с тем же
математическим ожиданием.

5.

f(Q)
1
x 2
Q1
Q2
Q
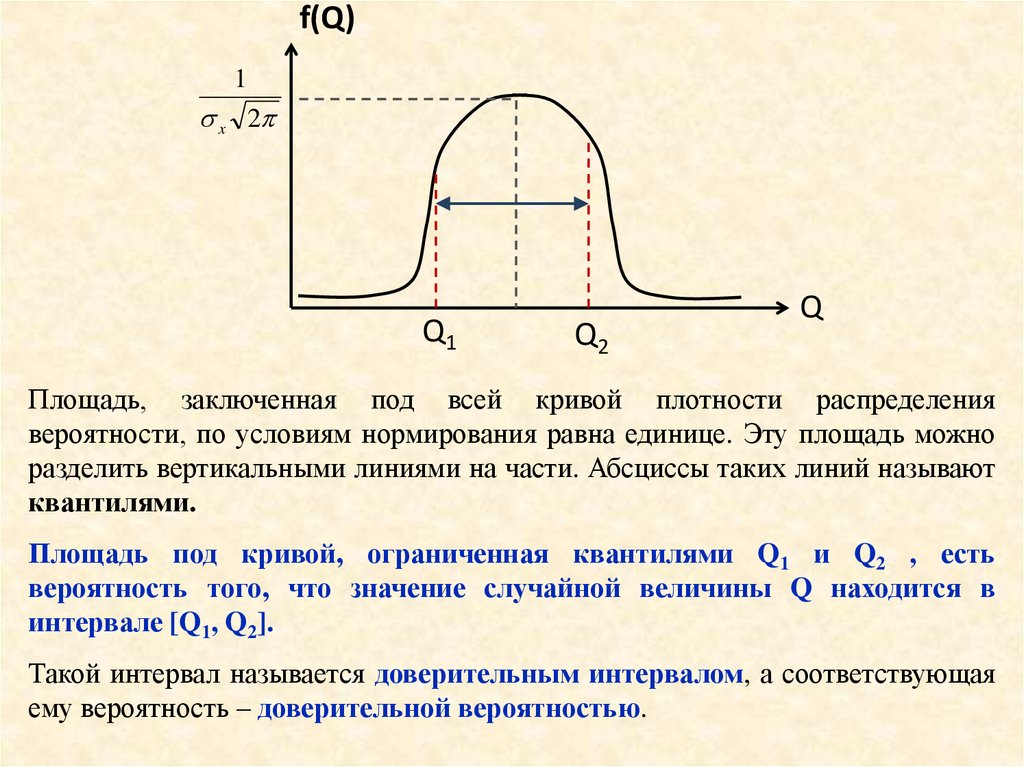
Площадь, заключенная под всей кривой плотности распределения
вероятности, по условиям нормирования равна единице. Эту площадь можно
разделить вертикальными линиями на части. Абсциссы таких линий называют
квантилями.
Площадь под кривой, ограниченная квантилями Q1 и Q2 , есть
вероятность того, что значение случайной величины Q находится в
интервале [Q1, Q2].
Такой интервал называется доверительным интервалом, а соответствующая
ему вероятность – доверительной вероятностью.

6.

Q1
- t S
‫ן‬
Q
+ t S
‫ן‬
Q2
‫ן‬
Границы доверительного интервала принято указывать симметрично
относительно
среднего
доверительного
арифметического
интервала
устанавливать
значения,
кратной
а
половину
СКП
(t·S)
и
принимать за оценку случайной погрешности результата измерения.
Применяется
также
термин
«доверительные
границы
случайной
погрешности». Доверительные границы случайной погрешности находят по
формуле:
= t S
где t – коэффициент, зависящий от доверительной вероятности Р и формы
закона распределения.

7.

Квантили, ограничивающие доверительный интервал, могут
быть
выбраны
любыми,
поэтому
при
интервальном
оценивании случайной погрешности необходимо указывать
значение принятой доверительной вероятности.
В целях единообразия интервальных оценок случайных
погрешностей при технических измерениях доверительная
вероятность принимается равной Р=0,95.
Если измерение нельзя повторить, ГОСТ 8.207-76 допускает
принимать Р=0,99.

8.

Если сравнить значения t, рассчитанные для разных
распределений,
то
при
Р
0,85
значения
t
максимальны для нормального распределения.
Поэтому при неизвестной функции распределения
(или при невозможности проверки принадлежности
результатов наблюдения к нормальному распределению)
рекомендуется распределение считать нормальным, т.к.
надежность оценки погрешности повышается.

9.

Критерий грубых погрешностей
При числе наблюдений n 30 и вероятности Р=0,9973 для
нормального распределения t = 3, т.е. с вероятностью 0,9973 все
случайные значения измеряемой величины попадают в интервал 3 .
Если
отклонение
результата
наблюдения
Qi
от
среднего
арифметического Q составляет больше 3σ,
Qi – Q 3σ
→ такое наблюдение содержит грубую погрешность, и должно быть
исключено при обработке результатов измерений.

10.

Определение случайных погрешностей
при неравноточных измерениях
Дано:
m групп независимых наблюдений одной и той же величины
Вычислены средние арифметические значения и оценки СКО:
ˆ x1 , ˆ x2 ,....., ˆ xm
x1 , x2 ,.....xm
S x1 , S x2 ,....., S xm
За результат измерения принимается оценка измеряемой величины по данным
всех групп наблюдений.
Эта оценка называется средним взвешенным:
m
x ajxj
j 1

11.

Коэффициенты aj
арифметического
отражают степень нашего доверия к оценкам среднего
xj
в каждой группе.
m
a
Коэффициенты aj - весовые коэффициенты
j 1
j
1
1
1
1
a1 : a2 : ... : am
:
: ... :
D ( x1 ) D ( x2 )
D( xm )
D( x j ) x j S x j
2
2
m
m
1
1
1
1
aj
:
:
2
2
D( x j ) j 1 D( x j ) S x j j 1 S x j

12.

Оценка СКО , т.е. СКП :
Sx
Sx
m
a
j 1
2
j
Sx j
1
m
S
j 1
1
2
xj
t S x
2

13.

Коэффициенты t определяются из таблицы для распределения
Стьюдента.
При этом предварительно определяется число степеней свободы
(n-1) распределения Стьюдента по формуле:
m2
(n 1) m
1
j 1 n j 1
m – число групп наблюдений
nj - число наблюдений в j-й группе.

14.

Определение случайных погрешностей
при косвенных измерениях
Q f x1 , x2 , x3 ,....xm
Q - искомая величина,
xi - величины, значения которых определяются прямым измерением.
За результат косвенного измерения принимается величина,
вычисляемая при подстановке в формулу для Q средних
арифметических значений xi .
Q f x1 , x2 , x3 ,....xm

15.

Общий прием - определение частных производных:
Q f ( x1 , x2 ...xm )
xi
xi
веса, с которыми в суммарную абсолютную погрешность Q
входят составляющие в виде абсолютных погрешностей
измерения каждого из xi .

16.

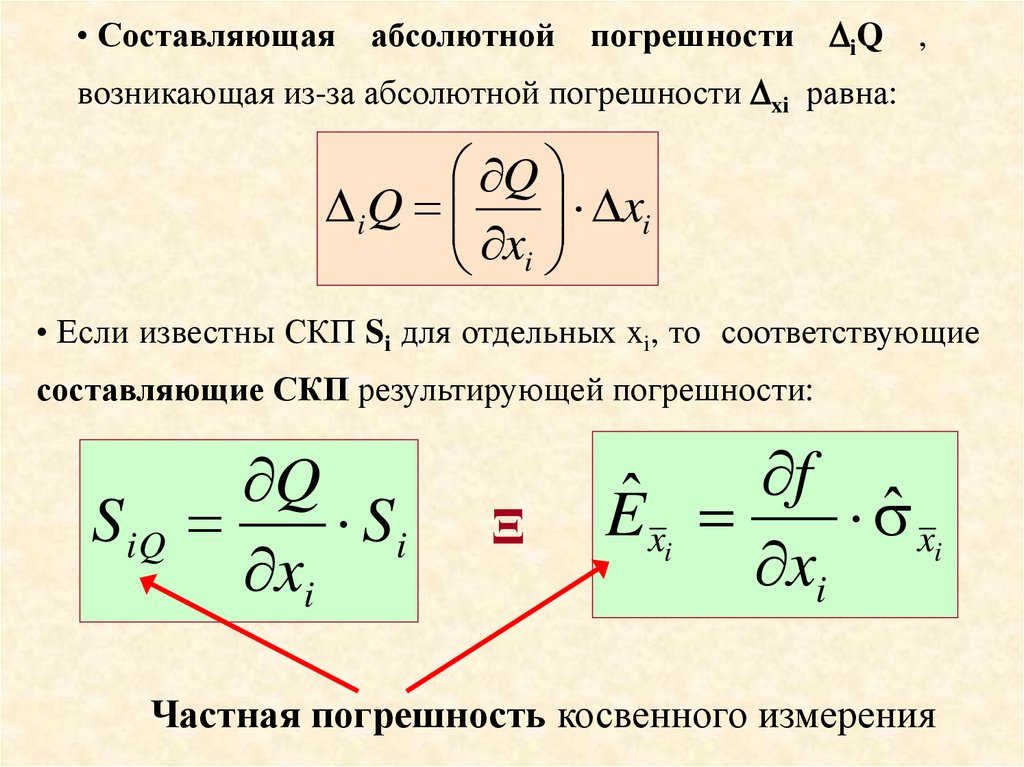
• Составляющая
абсолютной
погрешности
iQ
,
возникающая из-за абсолютной погрешности xi равна:
Q
xi
iQ
xi
• Если известны СКП Si для отдельных xi, то соответствующие
составляющие СКП результирующей погрешности:
Q
S iQ
Si
xi
Ξ
f
Eˆ xi
ˆ xi
xi
Частная погрешность косвенного измерения

17.

СКП функции нескольких переменных:
• если погрешности xi независимы и случайны:
m
2
ˆ
SQ ˆ Q Exi
i 1
Ξ
SQ
m
S
i 1
2
iQ

18.

СКП функции нескольких переменных:
• если между погрешностями измерения величин xi и xj
имеется корреляция:
m
m
i 1
i , j 1
i j
2
2 ˆ 2 ˆ
ˆ
ˆ
SQ ˆ Q Exi Exi Ex j Rij
2
m
f
f f
2
ˆ xi
SQ ˆ Q
ˆ xi ˆ x j Rˆij
i 1 xi
i , j 1 xi x j
m
i j
Производные вычисляются при:
xi xi
xj xj

19.

R̂ij
Оценка коэффициента корреляции между
погрешностями измерения величин xi и xj
1 Rˆij 1
R̂ij 0 положительная корреляция
R̂ij 0
отрицательная корреляция
R̂ij = 0 нет корреляции
1
Rˆij
xik xi x jk x j
n 1 ˆ xi ˆ x j k 1
n
n – наименьшее из числа наблюдений xik и xjk

20.

t S
Q
2
ˆ
Eˆ xi x i
i 1
m
1
2 ˆ 2
ˆ
E xi xi
i 1 ni 1
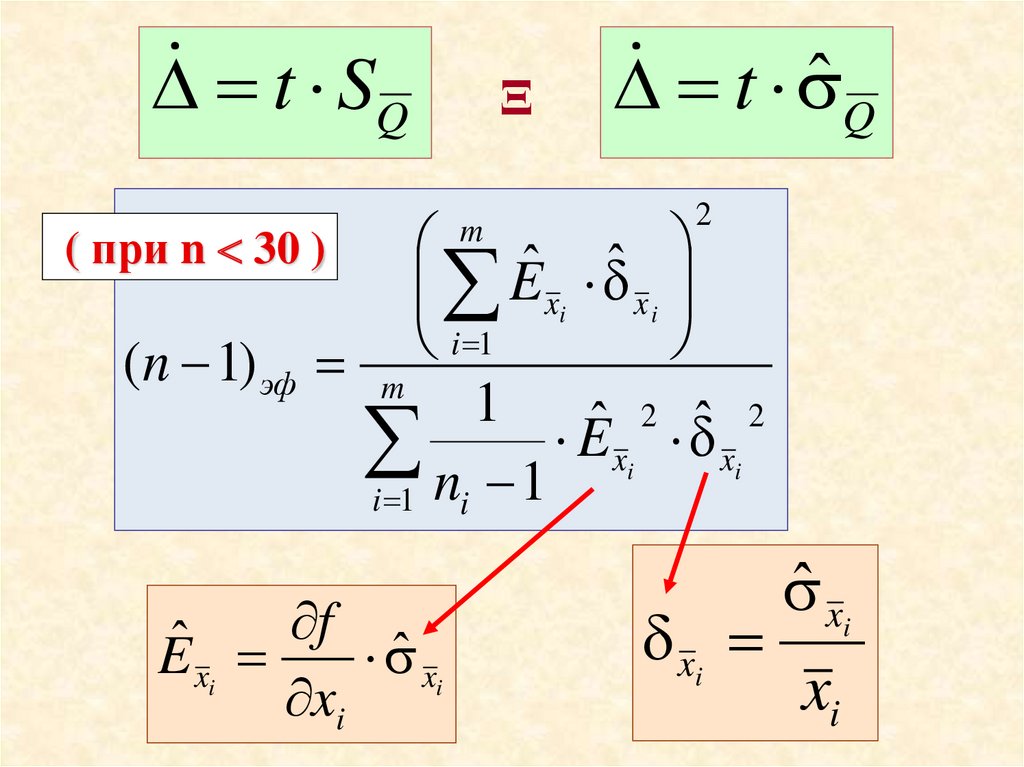
( при n 30 )
(n 1) эф
Ξ
t ˆ
Q
f
ˆ
E xi
ˆ xi
xi
m
xi
ˆ xi
xi

21.

Критерий ничтожных погрешностей
2
2
f
f
1,05 SQ
ˆ xi
ˆ xm 1
i 1 xi
xm 1
m
f
1
ˆ xm 1
ˆ Q
xm 1
3
1
ˆ
ˆ Q
Ξ Ex
m 1
3
Если частная погрешность меньше 1/3 соответствующей суммарной
погрешности, она может быть исключена из рассмотрения.

22.

Алгоритм обработки результатов многократных
наблюдений (при прямых и косвенных измерениях):
1.
Вводятся поправки для исключения всех известных систематических
эффектов. Все неисключенные систематические погрешности необходимо
просуммировать
между
собой
для
оценки
доверительных
границ
неисключенной систематической погрешности результата измерения Δс.
Суммарная НСП образуется из НСП метода, НСП поправок, НСП за счет
несовершенства применяемых СИ и т.д.
Все составляющие суммарной НСП рассматриваются как случайные
величины, и при отсутствии данных о виде распределения отдельных
составляющих
принимается гипотеза о равномерном распределении.
Границы НСП определяются по формуле:
с k
m
i 1
2
ci

23.

с k
ci
m
i 1
2
ci
- предельное значение i-й НСП,
m – число суммируемых погрешностей,
k- коэффициент, определяемый принятой доверительной вероятностью.
При Р = 0,95
k=1,1
При Р=0,99 k=1,4, если m 4
Если m 4, k определяется из графика
m
с ci
i 1
Дополнительно определяется, если m 4

24.

НСП при косвенных измерениях:
cx
i
f
c i
xi
Границы НСП результата
косвенного измерения
c k
m
i 1
2
cxi

25.

2. Проверяется принадлежность исправленных результатов наблюдений к
нормальному распределению. Или оно принимается таковым.
Правила такой проверки стандартизированы ГОСТ 11.006-74.
При n > 50 проверка производится с использованием критериев
Колмогорова (λn), Пирсона (χ2), или Мизеса-Смирнова (ω2).
Если 3< n <50 для проверки используется специальный критерий (W).
3.
Вычисляются:
• среднее арифметическое исправленных показаний,
• СКП в ряду измерений,
• СКП среднего арифметического .

26.

4.
Проверяется наличие грубых погрешностей или промахов (критерий
трех сигм). Показания, содержащие грубые погрешности, исключают из
массива данных и заново вычисляют среднее арифметическое и СКП.
5.
По заданной доверительной вероятности Р и числу наблюдений n
определяется
коэффициент
Стьюдента.
Для
прямых
равноточных
измерений его находят по таблице «коэффициенты t для распределения
Стьюдента»,
а
для
прямых
неравноточных
измерений
–
после
предварительного расчета числа степеней свободы (n-1). При косвенных
измерениях
прямое
пользование
таблицей
«коэффициенты
t
для
распределения Стьюдента» правомерно для n ≥ 30. Если же n < 30, то
предварительно должно быть рассчитано значение (n-1)эф . При дробных
значениях (n-1) и (n-1)эф осуществляется интерполяция.

27.

6.
Рассчитываются доверительные границы случайной
погрешности результата измерения
7. Вычисляют границы погрешности
t ˆ Q
результата измерений .
При этом необходимо проанализировать соотношения между НСП и
случайной погрешностью.
c
ˆ x
c
ˆ Q
0,8
=
8
= с
0,8 8
2
2
c
8. Записывают результат измерений по стандартной форме.

28.

Оценка погрешностей измерений с
однократными наблюдениями
Ожидаемую погрешность результата измерения оценивают
перед измерением на основе априорной информации.
1.
Проводится
анализ
составляющих
погрешности
результата
измерения по источникам возникновения. Анализируется модель
объекта, определяются влияющие факторы, оцениваются погрешности
метода, инструментальные погрешности (погрешности СИ), изучается
опыт выполнения подобных измерений.

29.

2.
После
исключения
систематических
погрешностей
неисключенные систематические погрешности суммируются для
определения
с .
(Аналогично процедуре при многократных
наблюдениях)
3.
Оценивается СКП результата измерения в предположении, что все
выявленные случайные погрешности независимы. С помощью
коэффициентов
Стьюдента
находятся
доверительные
границы
случайной погрешности .
Для однократных измерений приняты следующие значения t :
при Р=0,95
t=2;
при Р=0,99
t=2,6.

30.

4.
Производится оценка доверительных границ ожидаемой
суммарной погрешности результата измерения. По аналогии с
многократными
наблюдениями
рекомендуется
провести
сопоставление НСП и СКП
c
ˆ x
c
ˆ Q
8.
0,5
=
8
= с
0,5 8
0,8 c
Записывают результат измерений по стандартной форме.

31.

Стандартные правила представления результатов измерений
(регламентируются ГОСТ 8.011-72)
Основным способом выражения точности измерения является
задание интервала, в котором с установленной вероятностью
находится суммарная погрешность:
Q; от н до в; Р
При симметричной функции распределения результат измерения
можно записать в виде
Q ; Р
Числовое значение Q должно оканчиваться цифрой того же
разряда, что и значение .

32.

Если в суммарной погрешности результата измерения
превалирует систематическая составляющая :
Q;
с от сн до св; Р с ;
ˆ ( )
f
;
ст
Если значительны по уровню и систематические и
случайные погрешности:
Q ;
ˆ ( с ) ;
f
ст
с ;
ˆ ( )
;
f
ст

33.

При сложных измерениях, когда реальные функции
распределения вероятности значительно отличаются от
стандартных, эти функции целесообразно использовать
для выражения точности измерения:
Q ;
f с
;
f