Обработка экспериментальных данных при технических прямых и косвенных измерениях

1.

ПРАКТИЧЕСКАЯ РАБОТА №1
ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПРИ
ТЕХНИЧЕСКИХ ПРЯМЫХ И КОСВЕННЫХ ИЗМЕРЕНИЯХ
Цель работы: научиться обрабатывать экспериментальные данные при
технических измерениях.
Задание: Студентам предлагается самостоятельно решить семь
аналогичных задач по одному из вариантов из Приложений Ж–М.
Необходимо обратить внимание на соблюдение точности расчетов.
Методика выполнения
Задача 1
В результате измерений силы тока цифровым миллиамперметром
получен ряд значений:10,3924 мА, 10,2123 мА, 9,8534 мА, 9,7754 мА, 10,1545
мА, 9,9921мА.
Определить среднее значение и абсолютную и относительную
погрешности силы тока при доверительной вероятности α=0,95.
Решение
Среднее значение определяем по зависимости
n
1
x̄= ∑ x i
n i =1
(1)
n
∑ Ii
I ср= i =1 =10 , 0634 мА
n
Округление до четвертого знака после запятой произведено, так как
точность среднего значения не может быть выше точности результатов
исходных измерений.
Среднее квадратичное отклонение полученного результата
определяем по формуле
σ x̄ =
σ I ср=
√
n
√
n
∑ ( x̄ −x )2
i =1
(2)
n( n−1)
∑ ( I ср −I i )2
i=1
n(n−1 )
=0 , 0950 мА
Для расчета абсолютной погрешности воспользуемся формулой
X = x̄±Δx= x̄±t α , n−1 σ x̄
(3)
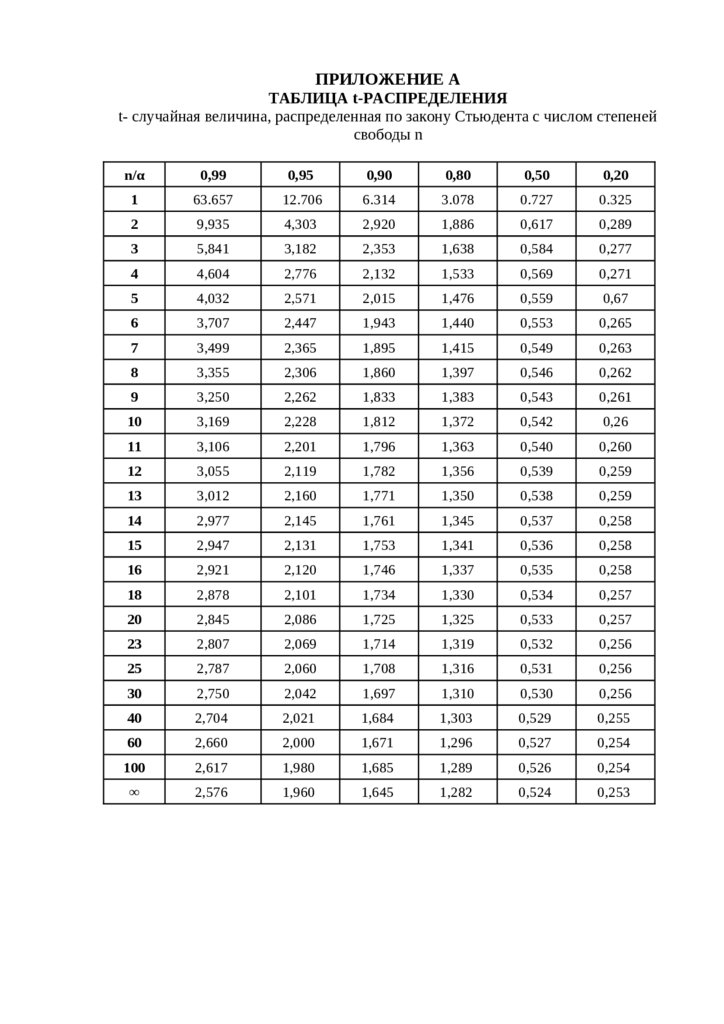
Входящий в формулу коэффициент Стьюдента tα,n-1 берем в таблице
распределения (приложение А) по доверительной вероятности 0,95 и числу
степеней свободы n–1=5, t0.95,5 = 2,571.
Рассчитываем абсолютную погрешность

2.

ΔI =t 0 . 95 , 5 σ I =0 ,2443 мА
Округляем
погрешности:
ср
результат
до второй значащей
цифры абсолютной
I=10 ,06±0,24 мА
Находим относительную погрешность по формуле
εx=
ε=
Δx
⋅100 %
x̄
(4)
ΔI
0 ,24
⋅100 %=
⋅100 %=2,4 %
I ср
10 , 06
Таким образом, можно сказать, что измеренное значение силы тока
равно (10,06±2,4%) мА.
Задача 2
Прибор для измерения длин волн электромагнитного излучения
аттестуется по стандартному излучению λэт=546,07 нм. При семи измерениях
получены результаты: 546,06 нм, 546,05 нм, 546,08 нм, 546,07 нм, 546,05 нм,
546,07 нм, 546,06 нм. Оценить систематическую погрешность измерений и
ширину доверительного интервала при доверительной вероятности 0,95.
Решение
Определяем среднее значение полученных результатов измерений по
зависимости (1)
n
λ ср=
∑ λi
i=1
n
=546 , 06 нм
Разница между истинным значением измеряемой величины и средним
значением результатов измерений и будет систематической погрешностью
(5)
Δλ сист =λ эт −λср ≈0 ,01
Ширину доверительного интервала – 2Δλ определяем как в
предыдущей задаче
σλ =
ср
нм.
√
n
∑ ( λ ср −λ i )2
i=1
n( n−1)
=0 , 0042 нм
Δλ=t 0 .95 , 6 σ λ =0 , 01 нм
ср
Таким образом, ширина доверительного интервала составляет 2Δλ=0,02
Задача 3
При измерении времени истечения жидкости через капилляр вискозиметра
получено 8 различных значений: 154,1 с; 154,4 с; 154,7с; 154,8 с; 155,2 с; 154,3 с;
154,3 с; 154,2 с. Проверить, является ли пятое измерение промахом?
Решение

3.

Выберем доверительную вероятность α = 0,95. Исключим из набора
значение t5 = 155,2 c. Вычислим среднее статистическое остальных семи
значений по формуле
n ,i ≠k
x̄ 1=
1
∑x
n−1 i =1 i
(6)
n , n≠5
∑ ti
i=1
t ср1 =
n−1
=154 , 4 c
Для α=0,95 и числа степеней свободы 8–2= 6 извлечем из таблицы
значение коэффициента Стьюдента t0,95,6 = 2,447.
Рассчитываем ширину интервала по формуле
√
Δx 1 =t⋅
√
Δt 1 =t⋅
n ,i ≠k
n⋅ ∑ ( xi − x̄ 1 )
i =1
(7)
( n−1)⋅( n−2 )
n, i≠k
n⋅ ∑ ( t i −t cр 1 )
i=1
( n−1 )⋅( n−2)
≈0 ,76 с
Отклонение проверяемого измерения t5 от среднего значения tср
остальных результатов значительно превышает t1 ,поэтому величину t5
следует признать промахом и исключить из набора результатов.
Задача 4
Диаметр цилиндра измерялся пять раз микрометром c приборной
погрешностью δ = 0,01 мм. При этом были получены следующие числовые
значения: 15,32 мм; 15,31 мм; 15,29 мм; 15,31 мм; 15,32 мм.
Требуется определить абсолютную и относительную погрешности
измерения диаметра d, а также границы доверительного интервала для
заданной доверительной вероятности α=0,95.
Решение
Сначала рассчитываем среднее значение диаметра по формуле (1) и
получаем
n
d ср =
∑ di
i=1
n
=15 ,31 нм
Прежде чем вычислять d, следует провести предварительный анализ
данных.
Все разности (dср–di) по абсолютной величине соизмеримы с δ,
следовательно, необходимо учесть и случайную, и приборную составляющие
погрешности. По формуле (2) получаем:

4.

σ d ср =
√
n
∑ ( d ср −d i )2
i=1
n( n−1)
=0 , 006 мм
Выбираем доверительную вероятность (надежность) 0,95. Так как
серия измерений содержит пять значений, то коэффициент Стьюдента
следует брать для числа степеней свободы равного 4. Из таблицы
коэффициентов Стьюдента извлекаем значение t0,95;4 =2,776.
Для той же доверительной вероятности 0,95 и для бесконечного числа
степеней свободы значение коэффициента Стьюдена t0,95; ∞ =1,960. Далее
рассчитываем по формуле
√
δ
X = x̄± (t α , n−1 σ x̄ )2 +(t α , ∞ )2
3
δ
d=d ср± (t α , n−1 σ d )2 +(t α , ∞ )2 =15 ,31±0 , 02 мм
ср
3
√
(8)
Эта запись означает, что истинное значение диаметра цилиндра с
вероятностью 0,95 находится внутри доверительного интервала с границами
(15,29 мм;15,33 мм).
Относительную погрешность считаем по зависимости (4)
εx=
Δd
⋅100 %=0 , 11%
d ср
Таким образом, можно записать результат
d=15,31 мм±0,11%

5.

ПРИЛОЖЕНИЕ А
ТАБЛИЦА t-РАСПРЕДЕЛЕНИЯ
t- случайная величина, распределенная по закону Стьюдента с числом степеней
свободы n
n/α
0,99
0,95
0,90
0,80
0,50
0,20
1
63.657
12.706
6.314
3.078
0.727
0.325
2
9,935
4,303
2,920
1,886
0,617
0,289
3
5,841
3,182
2,353
1,638
0,584
0,277
4
4,604
2,776
2,132
1,533
0,569
0,271
5
4,032
2,571
2,015
1,476
0,559
0,67
6
3,707
2,447
1,943
1,440
0,553
0,265
7
3,499
2,365
1,895
1,415
0,549
0,263
8
3,355
2,306
1,860
1,397
0,546
0,262
9
3,250
2,262
1,833
1,383
0,543
0,261
10
3,169
2,228
1,812
1,372
0,542
0,26
11
3,106
2,201
1,796
1,363
0,540
0,260
12
3,055
2,119
1,782
1,356
0,539
0,259
13
3,012
2,160
1,771
1,350
0,538
0,259
14
2,977
2,145
1,761
1,345
0,537
0,258
15
2,947
2,131
1,753
1,341
0,536
0,258
16
2,921
2,120
1,746
1,337
0,535
0,258
18
2,878
2,101
1,734
1,330
0,534
0,257
20
2,845
2,086
1,725
1,325
0,533
0,257
23
2,807
2,069
1,714
1,319
0,532
0,256
25
2,787
2,060
1,708
1,316
0,531
0,256
30
2,750
2,042
1,697
1,310
0,530
0,256
40
2,704
2,021
1,684
1,303
0,529
0,255
60
2,660
2,000
1,671
1,296
0,527
0,254
100
2,617
1,980
1,685
1,289
0,526
0,254
∞
2,576
1,960
1,645
1,282
0,524
0,253

6.

х1
2
36,977
106,14
37,515
0,0303
107,06
106,84
35,646
106,8
0,0299
105,04
38,782
109,21
0,0303
105,92
107,09
Вариант
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0,0301
110,06
107,12
37,541
107,36
0,0299
107,73
35,257
108,47
0,0302
105,47
108,82
38,044
109,69
37,184
3
х2
0,0298
108,55
107,22
38,957
107,66
0,0301
109,04
38,354
108,99
0,0299
107,23
108,54
38,761
108,76
37,059
4
х3
0,0298
106,71
110,63
36,134
109,2
0,03
108,48
36,993
107,88
0,0297
106,26
107,62
36,165
108,11
36,537
5
х4
0,03
105,94
109,06
36,786
107,45
0,0304
106,78
35,819
108,23
0,0302
107,12
107,84
36,79
108,21
36,663
6
х5
0,030
106,3
109,0
37,76
106,9
0,030
107,9
36,09
107,6
0,03
108,4
107,2
36,13
108,8
38,85
7
х6
0,03
108,9
109,13
37,075
110,3
0,0302
107,9
35,864
112,46
0,0301
109,84
108,88
37,303
108,04
36,819
8
х7
0,0301
107,89
109,76
37,368
106,87
0,0302
106,77
108,75
0,0303
107,41
107,07
36,785
105,36
36,788
9
х8
0,0302
107,36
107,85
36,979
110,6
0,0297
17,63
107,22
0,03
106,68
38,671
108,67
36,424
10
х9
106,37
36,076
0,0302
107,04
0,0299
-
37,68
105,08
-
11
х10
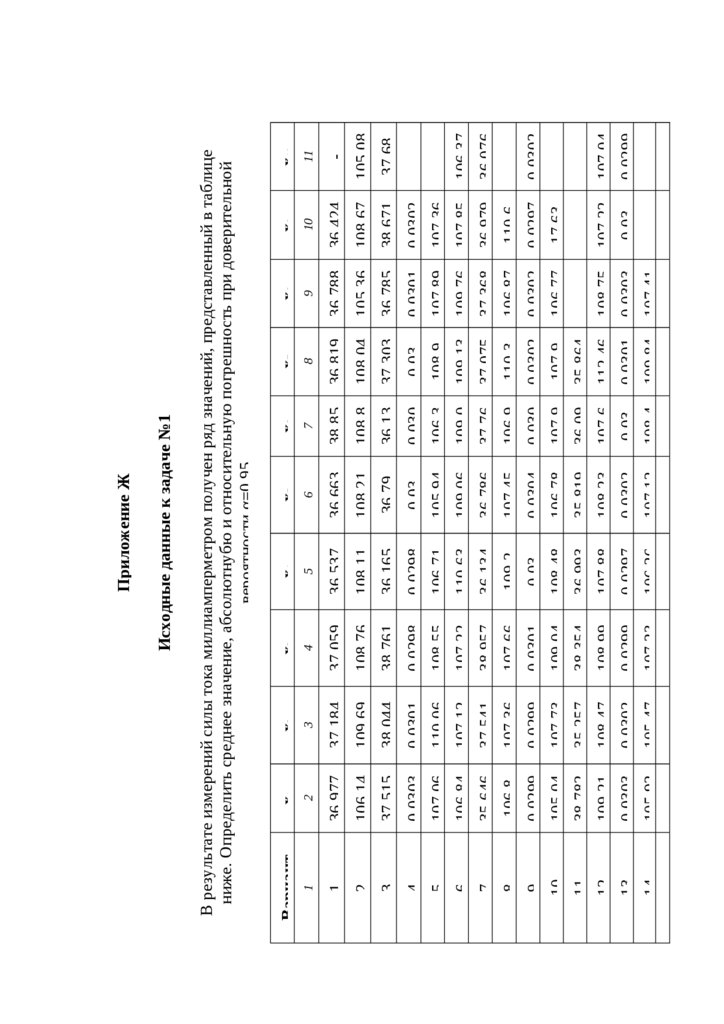
В результате измерений силы тока миллиамперметром получен ряд значений, представленный в таблице
ниже. Определить среднее значение, абсолютнубю и относительную погрешность при доверительной
вероятности α=0,95
Исходные данные к задаче №1
Приложение Ж

7.

ПРИЛОЖЕНИЕ И
х1
2
108,25
0,03
37,584
35,5
0,03
35,52
107,84
109,18
38,364
35,887
0,03
105,44
0,0294
37,032
109,22
Вариант
1
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
107,99
108,73
36,418
38,683
0,0299
108,53
0,0301
36,361
106,91
35,017
0,0299
37,909
37,447
0,03
106,95
3
х2
108,7
108,99
35,326
37,105
0,0298
108,02
0,0304
36,698
109,95
36,279
0,0302
38,422
38,564
0,0302
109,26
4
х3
107,2
105,82
37,319
36,114
0,0297
107,26
0,0301
38,242
106,99
37,191
0,0297
37,525
37,391
0,0299
109,92
5
х4
108,65
108,17
37,998
38,002
0,0302
107,53
0,0299
37,387
106,44
37,75
0,0301
36,691
36,491
0,0301
108,79
6
х5
105,6
107,8
36,09
36,57
0,030
107,8
0,030
36,16
108,9
37,02
0,030
36,41
37,98
0,029
107,5
7
х6
105,97
107,41
38,188
37,825
0,0303
109,08
0,0303
36,965
107,03
37,385
0,0301
37,782
37,186
0,0299
107,72
8
х7
106,46
107,46
36,024
37,083
0,0299
109,39
0,03
36,601
109,52
36,76
0,0298
37,046
-
0,0299
108,43
9
х8
108,9
108,75
35,815
38,22
0,03
0,0302
35,409
107,72
-
-
36,344
-
0,0304
-
10
х9
36,285
0,03
0,0298
38,47
104,66
-
-
-
-
-
-
11
х10
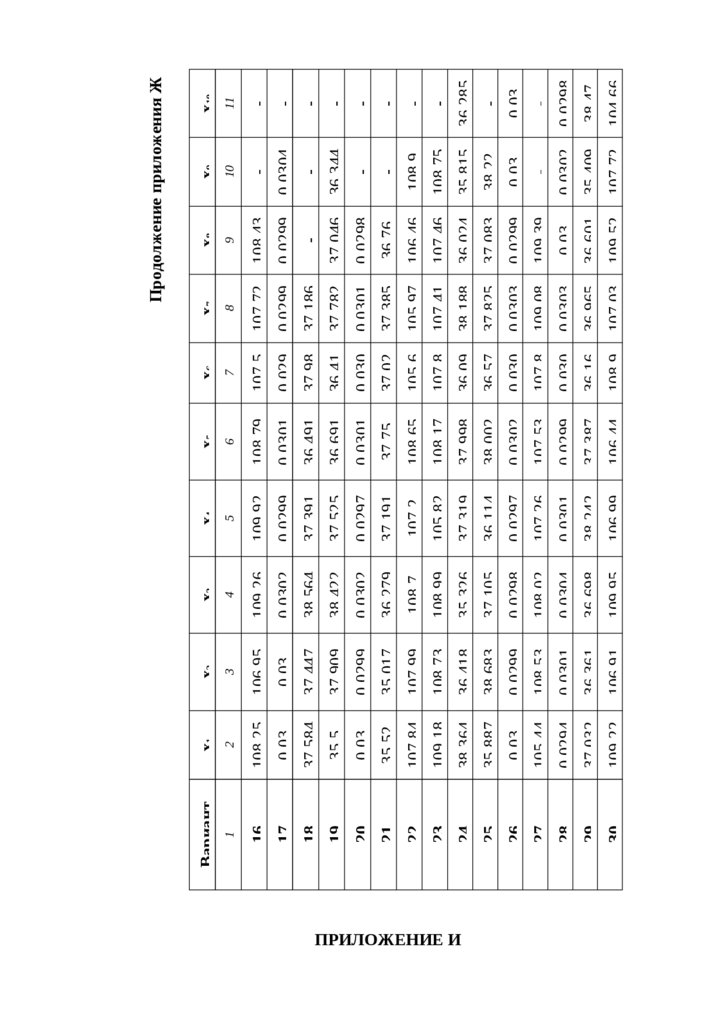
Продолжение приложения Ж

8.

Исходные данные к задаче №2
Электронные лабораторные весы калибруются по эталонному грузу
0,001г Проводится 6 измерений. Результаты в таблице ниже. Определить
систематическую погрешность и доверительный интервал при доверительной
вероятности 0,95
Вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
x1
0,00123
0,00115
0,00116
0,00117
0,00095
0,00120
0,00109
0,00104
0,00102
0,00119
0,00112
0,00119
0,00115
0,00127
0,00116
0,00114
0,00117
0,00132
0,00101
0,00108
0,00134
0,00141
0,00107
0,00123
0,00112
0,00114
0,00138
0,00099
0,00125
0,00117
x2
0,00126
0,00093
0,00110
0,00109
0,00115
0,00116
0,00115
0,00118
0,00127
0,00124
0,00123
0,00114
0,00123
0,00127
0,00134
0,00107
0,00124
0,00118
0,00098
0,00082
0,00122
0,00098
0,00110
0,00093
0,00107
0,00105
0,00127
0,00131
0,00126
0,00131
x3
0,00129
0,00093
0,00114
0,00126
0,00127
0,00122
0,00123
0,00091
0,00112
0,00122
0,00097
0,00154
0,00113
0,00099
0,00130
0,00128
0,00108
0,00109
0,00086
0,00119
0,00113
0,00120
0,00112
0,00099
0,00112
0,00090
0,00113
0,00128
0,00085
0,00106
x4
0,00107
0,00116
0,00122
0,00124
0,00121
0,00097
0,00139
0,00122
0,00102
0,00120
0,00083
0,00106
0,00133
0,00112
0,00132
0,00124
0,00113
0,00107
0,00106
0,00119
0,00124
0,00114
0,00124
0,00110
0,00100
0,00086
0,00123
0,00131
0,00111
0,00114
ПРИЛОЖЕНИЕ К
x5
0,00120
0,00096
0,00116
0,00115
0,00096
0,00116
0,00121
0,00118
0,00111
0,00121
0,00112
0,00120
0,00106
0,00118
0,00112
0,00086
0,00095
0,00096
0,00123
0,00113
0,00122
0,00101
0,00125
0,00117
0,00098
0,00106
0,00122
0,00101
0,00114
0,00121
x6
0,00109
0,00093
0,00128
0,00130
0,00114
0,00124
0,00132
0,00135
0,00107
0,00134
0,00111
0,00135
0,00118
0,00121
0,00110
0,00104
0,00089
0,00114
0,00099
0,00115
0,00127
0,00117
0,00117
0,00124
0,00131
0,00097
0,00112
0,00120
0,00107
0,00091

9.

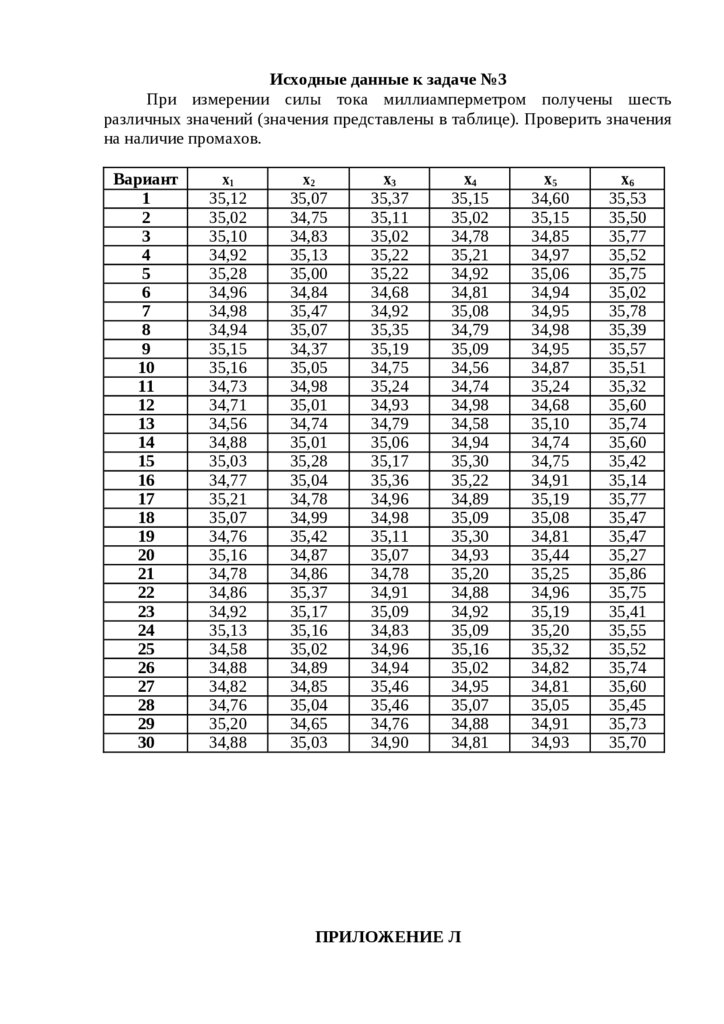
Исходные данные к задаче №3
При измерении силы тока миллиамперметром получены шесть
различных значений (значения представлены в таблице). Проверить значения
на наличие промахов.
Вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
x1
35,12
35,02
35,10
34,92
35,28
34,96
34,98
34,94
35,15
35,16
34,73
34,71
34,56
34,88
35,03
34,77
35,21
35,07
34,76
35,16
34,78
34,86
34,92
35,13
34,58
34,88
34,82
34,76
35,20
34,88
x2
35,07
34,75
34,83
35,13
35,00
34,84
35,47
35,07
34,37
35,05
34,98
35,01
34,74
35,01
35,28
35,04
34,78
34,99
35,42
34,87
34,86
35,37
35,17
35,16
35,02
34,89
34,85
35,04
34,65
35,03
x3
35,37
35,11
35,02
35,22
35,22
34,68
34,92
35,35
35,19
34,75
35,24
34,93
34,79
35,06
35,17
35,36
34,96
34,98
35,11
35,07
34,78
34,91
35,09
34,83
34,96
34,94
35,46
35,46
34,76
34,90
x4
35,15
35,02
34,78
35,21
34,92
34,81
35,08
34,79
35,09
34,56
34,74
34,98
34,58
34,94
35,30
35,22
34,89
35,09
35,30
34,93
35,20
34,88
34,92
35,09
35,16
35,02
34,95
35,07
34,88
34,81
ПРИЛОЖЕНИЕ Л
x5
34,60
35,15
34,85
34,97
35,06
34,94
34,95
34,98
34,95
34,87
35,24
34,68
35,10
34,74
34,75
34,91
35,19
35,08
34,81
35,44
35,25
34,96
35,19
35,20
35,32
34,82
34,81
35,05
34,91
34,93
x6
35,53
35,50
35,77
35,52
35,75
35,02
35,78
35,39
35,57
35,51
35,32
35,60
35,74
35,60
35,42
35,14
35,77
35,47
35,47
35,27
35,86
35,75
35,41
35,55
35,52
35,74
35,60
35,45
35,73
35,70

10.

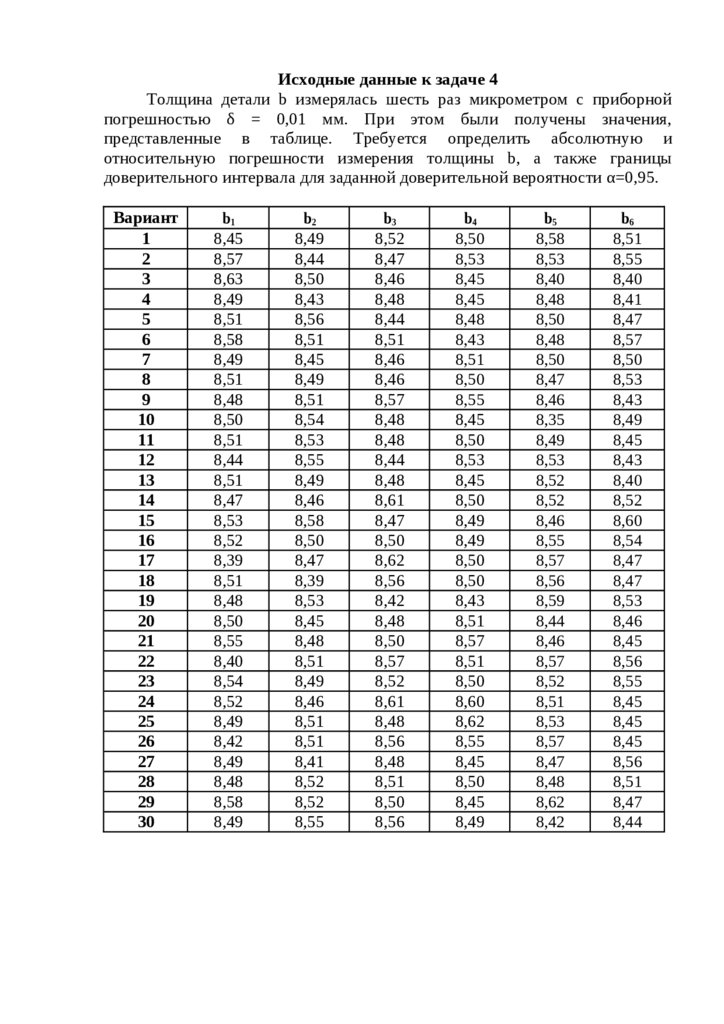
Исходные данные к задаче 4
Толщина детали b измерялась шесть раз микрометром c приборной
погрешностью δ = 0,01 мм. При этом были получены значения,
представленные в таблице. Требуется определить абсолютную и
относительную погрешности измерения толщины b, а также границы
доверительного интервала для заданной доверительной вероятности α=0,95.
Вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
b1
8,45
8,57
8,63
8,49
8,51
8,58
8,49
8,51
8,48
8,50
8,51
8,44
8,51
8,47
8,53
8,52
8,39
8,51
8,48
8,50
8,55
8,40
8,54
8,52
8,49
8,42
8,49
8,48
8,58
8,49
b2
8,49
8,44
8,50
8,43
8,56
8,51
8,45
8,49
8,51
8,54
8,53
8,55
8,49
8,46
8,58
8,50
8,47
8,39
8,53
8,45
8,48
8,51
8,49
8,46
8,51
8,51
8,41
8,52
8,52
8,55
b3
8,52
8,47
8,46
8,48
8,44
8,51
8,46
8,46
8,57
8,48
8,48
8,44
8,48
8,61
8,47
8,50
8,62
8,56
8,42
8,48
8,50
8,57
8,52
8,61
8,48
8,56
8,48
8,51
8,50
8,56
b4
8,50
8,53
8,45
8,45
8,48
8,43
8,51
8,50
8,55
8,45
8,50
8,53
8,45
8,50
8,49
8,49
8,50
8,50
8,43
8,51
8,57
8,51
8,50
8,60
8,62
8,55
8,45
8,50
8,45
8,49
b5
8,58
8,53
8,40
8,48
8,50
8,48
8,50
8,47
8,46
8,35
8,49
8,53
8,52
8,52
8,46
8,55
8,57
8,56
8,59
8,44
8,46
8,57
8,52
8,51
8,53
8,57
8,47
8,48
8,62
8,42
b6
8,51
8,55
8,40
8,41
8,47
8,57
8,50
8,53
8,43
8,49
8,45
8,43
8,40
8,52
8,60
8,54
8,47
8,47
8,53
8,46
8,45
8,56
8,55
8,45
8,45
8,45
8,56
8,51
8,47
8,44