Измерения. Прямые. Косвенные

1.

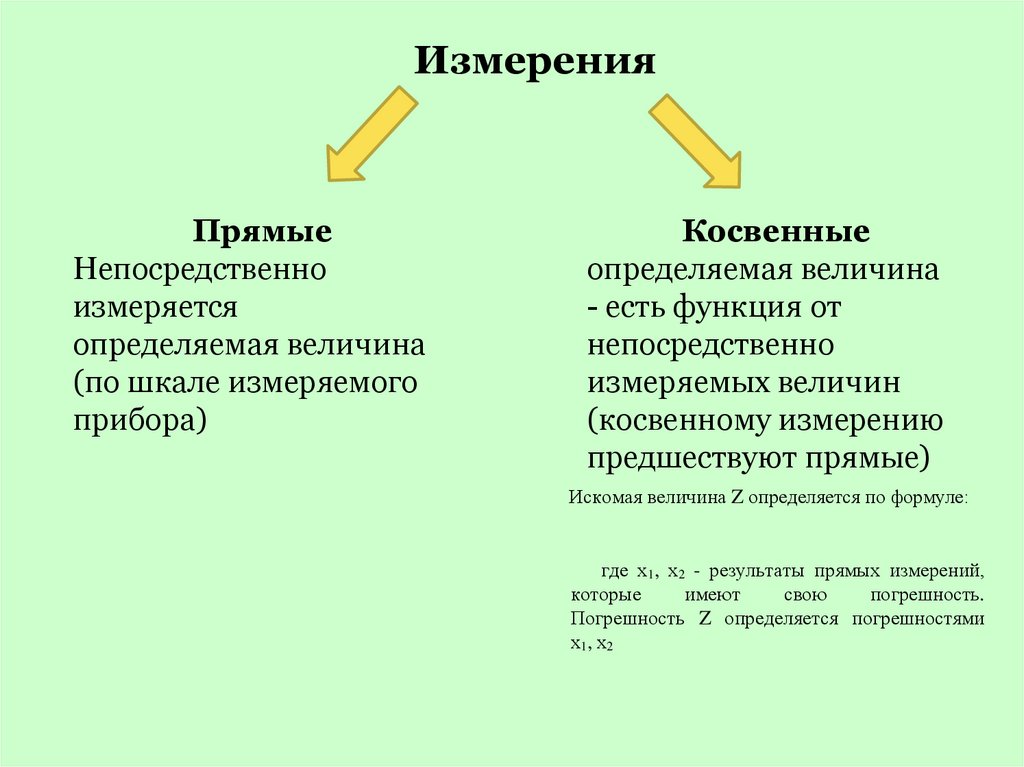
Измерения
Прямые
Непосредственно
измеряется
определяемая величина
(по шкале измеряемого
прибора)
Косвенные
определяемая величина
- есть функция от
непосредственно
измеряемых величин
(косвенному измерению
предшествуют прямые)
Искомая величина Z определяется по формуле:
где х1, х2 - результаты прямых измерений,
которые
имеют
свою
погрешность.
Погрешность Z определяется погрешностями
х1, х2

2.

Каждый результат экспериментального измерения —
случайная величина - величина, принимающая в
результате испытания значение, которое принципиально
нельзя
предсказать,
исходя
из
условий
опыта.
Случайная величина обладает целым набором
допустимых значений, но в результате каждого отдельного
опыта принимает лишь какое-то одно из них.
- Случайная величина изменяет свое значение даже при
неизменных условиях опыта.
/

3.

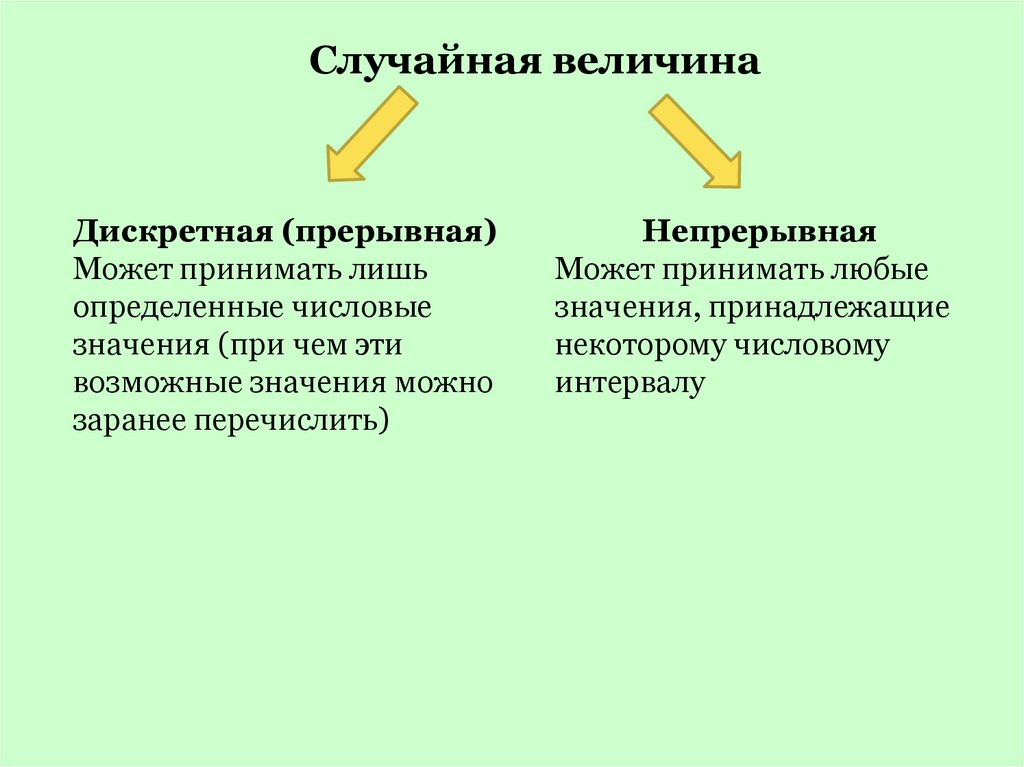
Случайная величина
Дискретная (прерывная)
Может принимать лишь
определенные числовые
значения (при чем эти
возможные значения можно
заранее перечислить)
Непрерывная
Может принимать любые
значения, принадлежащие
некоторому числовому
интервалу

4.

Классификация
измерений
ошибок
А — истинное значение исследуемой величины,
а — опытное значение (обычно среднее арифметическое
серии измерений).
Абсолютная ошибка (или погрешность) величины а
-абсолютное значение разности между истинным и опытным
значениями:
= А – а = а ,
Или
А = а .
!Абсолютная ошибка - - в тех же единицах, что и сама
величина

5.

Классификация
А — иси
тизнм
ное
ер
зне
ач
е исследуемой величины,
нениий
ошибок
а — опытное значение
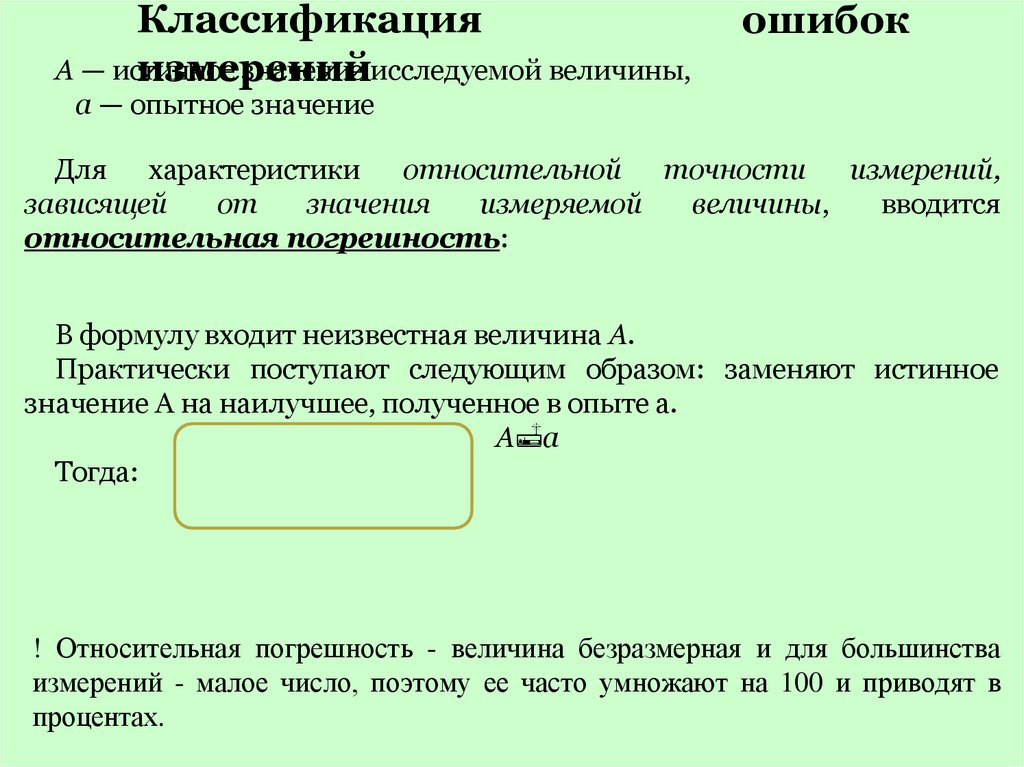
Для характеристики
относительной точности
измерений,
зависящей
от
значения
измеряемой
величины,
вводится
относительная погрешность:
В формулу входит неизвестная величина А.
Практически поступают следующим образом: заменяют истинное
значение А на наилучшее, полученное в опыте а.
А а
Тогда:
! Относительная погрешность - величина безразмерная и для большинства
измерений - малое число, поэтому ее часто умножают на 100 и приводят в
процентах.

6.

7.

.
Законом распределения случайной величины
называют любое соотношение, устанавливающее
связь между возможными значениями случайной
величины и соответствующими им вероятностями.
При большом количестве опытов (в пределе
n ) частота появления события (mi/n)
стабилизируется около некоторого значения рi,
называемого вероятностью события
Пусть СВ Х может принимать значения х1, х2, …, хn.
mi - число опытов, в результате которых СВ Х принимает значение хi, n
- общее число опытов.
Частота появления события, что СВ Х=хi, равна отношению (mi / n)
Частота (mi / n) является случайной величиной и меняется в
зависимости от количества проведенных опытов.

8.

Оценка погрешностей функций приближенных
аргументов
Измеренная величина
умножается на точное число.
Z = BX
В — точное число, Х± x - результат прямых
измерений

9.

Оценка погрешностей функций приближенных
аргументов
Погрешность в суммах и разностях.
Z = (X1 + Х2) – (Х3 + Х4)
Если погрешности аргументов Хi независимы и
случайны, то погрешность в Z равна квадратичной
сумме исходных погрешностей:
погрешность Z никогда не больше, чем обычная сумма
погрешностей аргументов
Т.е. предельная погрешность:

10.

Оценка погрешностей функций приближенных
аргументов
Погрешность в произведениях и частных
Если погрешности аргументов Хi независимы и
случайны, то относительная погрешность в Z равна
квадратичной
сумме
исходных
относительных
погрешностей :
погрешность Z никогда не больше, чем обычная сумма
погрешностей аргументов
Т.е. предельная погрешность:

11.

Оценка погрешностей функций приближенных
аргументов
Погрешность в степенной функции.
где m — фиксированное известное число,
Относительная погрешность Z в m раз больше, чем в Х

12.

Оценка погрешностей функций приближенных
аргументов
Погрешность в произведениях, частных,
степенной функции.
где m, n, l — фиксированные известные числа

13.

Оценка погрешностей функций приближенных
аргументов
Метод «шаг за шагом»
Расчет нужно представить как последовательность шагов:
1) нахождение сумм и разностей,
2) расчет произведений и частных,
3) вычисление функции одного переменного
НО! В случае когда выражение для вычисления функции Z включает одну и
ту же прямо измеряемую величину более чем один раз (например, дважды Х1),
то некоторые из ошибок могут взаимно компенсироваться и в результате
расчет ошибки методом «шаг за шагом» может привести к переоценке
конечной погрешности.
В подобных случаях нужно пользоваться общей формулой:

14.

.
Дискретную СВ можно задать вероятностным
рядом (одним из видов законов распределения).
х1
р1
Очевидно, что:
х2
р2
х3
р3
…
…
хn
рn

15.

.
Распределение СВ (непрерывной и дискретной)
можно задать в виде функции распределения
F(x) - функция распределения
(предельная функция распределения, функция
распределения генеральной совокупности)
Функция распределения равна вероятности того, что
значение СВ Х будет меньше или равно какому-то
произвольному значению х.
F(x) = Р (Х х)
т.е. вероятность того, что получим значение
СВ, лежащее левее х, равна 60%.

16.

Функция распределения
непрерывной СВ.
F(х2) - F(х1) - вероятность того, что значение СВХ
примет в результате опыта величину от х1 до х2
F(х2) - F(х1)=Р(х1 Х х2)

17.

.
Для непрерывной СВ F(x) является неубывающей
функцией, т.е. если х1 х2, то F(х1) F(х2)
Вероятность того, что значения СВ будут лежать в
интервале от х1 до х2, равна
Р(х1 Х х2) = F(х2) - F(х1).
Пример:
т.е. вероятность того, что значение СВХ примет в
результате опыта величину от х1 до х2 равна 20%.

18.

Для непрерывной случайной величины используется
производная функции распределения — плотность
распределения случайной величины Х.
Заштрихованная площадь равна вероятности того, что
случайная величина примет значения из интервала х1 х2:

19.

Полный набор всех возможных значений СВ –
генеральная совокупность
Универсальный способ ее описания –
использование функции и плотности
распределения (F(x), f(x))
Но: для получения F(x) и f(x) в ряде случаев
необходимы трудоемкие исследования и
расчеты.

20.

Выход:
В прикладных задачах СВ часто определяют при
помощи
числовых
характеристик
— чисел,
выражающих характерные особенности случайной
величины,
называемых моментами случайной
величины.
В математической статистики часто используют:
1) математическое ожидание
- характеризует
положение значений случайной величины на
числовой оси
2) дисперсию (или среднее квадратичное
отклонение) - определяет характер разброса
значений случайной величины.

21.

Математическое ожидание случайной величины
(генеральное среднее, начальный момент первого
порядка)
Принято обозначать М [Х], mx или m.
Для дискретной случайной величины:
Для непрерывной случайной величины:
Для непрерывных случайных величин математическое
ожидание является теоретической величиной, к которой
приближается среднее значение случайной величины при
большом количестве испытаний

22.

Свойства математического ожидания
1. Если с — постоянное число (неслучайная величина), то
М [c] = c,
М [cХ] = c М [Х].
2. Математическое ожидание суммы случайных величин равно
сумме математических ожиданий этих случайных величин:
М [Х1 + Х2 + …+ Хn] = М [Х1] + М [Х2] + … + М [Хn].
3. Математическое ожидание произведения независимых
случайных величин равно произведению математических
ожиданий сомножителей:
М [Х1 Х2 Х3 … Хn] = М [Х1] М [Х2] М [Х3] … М [Хn].
4. Если случайная величина Z является некоторой нелинейной
функцией n независимых случайных величин
Z = f (X1,
X2, …, Хn), которая мало меняется в небольших интервалах
изменения аргументов, то

23.

Дисперсия случайной величины
(второй центральный момент)
Обозначение: D [X]=Д(Х)=σ2= x 2= 2(X).
Дисперсией
называется
математическое
ожидание
квадрата отклонения случайной величины от ее
математического ожидания, т. е.
σ2= M [(X – mx)2]
Для непрерывной случайной величины:
Корень квадратный из дисперсии
квадратичным
отклонением
отклонением, или стандартом)
называется средним
(стандартным

24.

Свойства дисперсии
1. Если с — постоянное число (неслучайная величина), то
2(c) = 0, 2(cХ) = с2 2(Х).
2. Дисперсия случайной величины равна математическому
ожиданию квадрата случайной величины минус квадрат ее
математического ожидания:
3. Дисперсия суммы независимых СВ равна сумме дисперсий этих
величин: 2(Х1 + Х2 +…+ Хn) = 2(Х1) + 2(Х2) + … + 2(Хn).
-закон сложения дисперсий - справедлив для дисперсий ( 2), а не
среднеквадратичных отклонений ( ).
4. Если СВ Z является нелинейной функцией n независимых СВ Z
= f (X1, X2, …, Хn), которая мало меняется в небольших интервалах
изменения аргументов, то ее дисперсия приближенно равна:
- закон накопления ошибок, (часто используется для определения
случайной ошибки функции по значениям случайных ошибок
аргументов)

25.

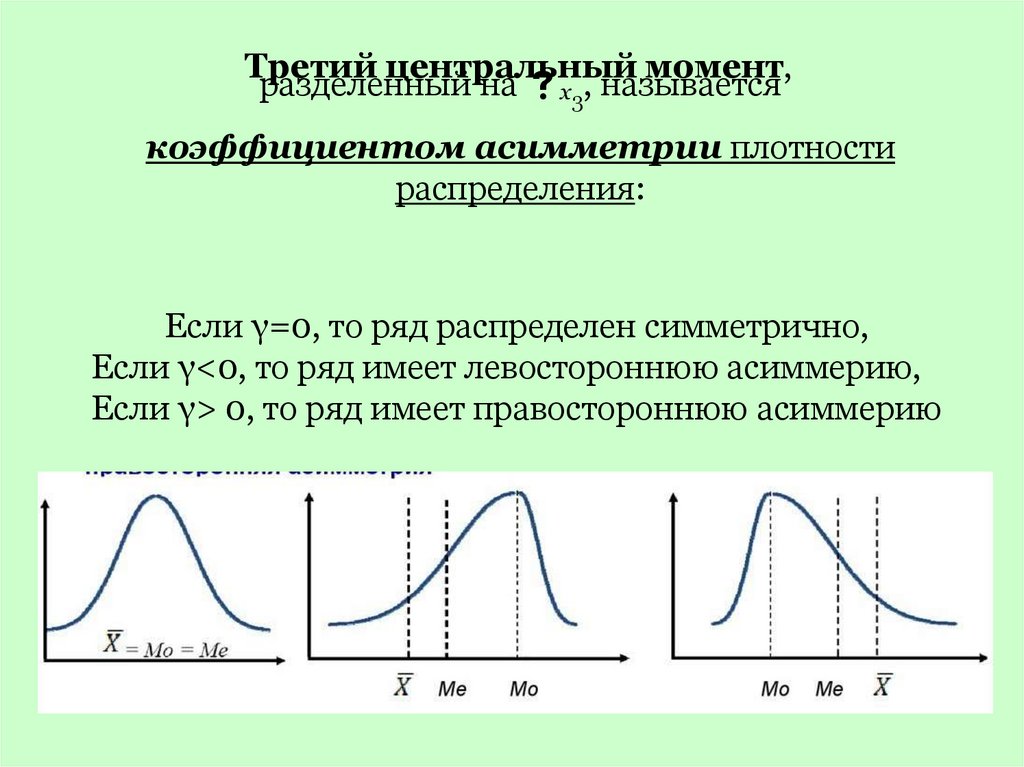
Третий центральный момент,
разделенный на x3, называется
коэффициентом асимметрии плотности
распределения:
Если γ=0, то ряд распределен симметрично,
Если γ<0, то ряд имеет левостороннюю асиммерию,
Если γ> 0, то ряд имеет правостороннюю асиммерию

26.

.
Непрерывная случайная величина Х называется распределенной по
нормальному закону, если ее плотность распределения имеет вид
Функция распределения равна
График плотности нормального распределения называется нормальной
кривой, или кривой Гаусса
Условие нормировки плотности
распределения:

27.

.
Непрерывная случайная величина Х называется распределенной по
нормальному закону, если ее плотность распределения имеет вид
Функция распределения равна
Замена некоторого распределения нормальным распределением
не приводит к переоценки точности эксперимента.
Действительное распределение с какой-то дисперсией заменяем
на нормальное распределение с той же дисперсией
Обработка результатов по стандартным методикам

28.

Нормальный закон распределения – хорошая модель для
реальных явлений, в которых:
1) Имеется тенденция данных группироваться вокруг центра;
2)
Равновероятны
положительные
и
отрицательные
отклонения от центра;
Ошибки измерения неизбежно сопутствуют любому
измерению случайной величины
Ошибка измерения рассматривается как сумма большого
числа взаимно независимых элементарных (частных) ошибок,
которые сопоставимы по размеру.
+
Элементарные ошибки равномерно входят в каждое
измерение как со знаком «плюс», так и со знаком «минус».
Каковы бы не были законы распределения элементарных
ошибок, закон распределения их суммы будет близок к
нормальному.

29.

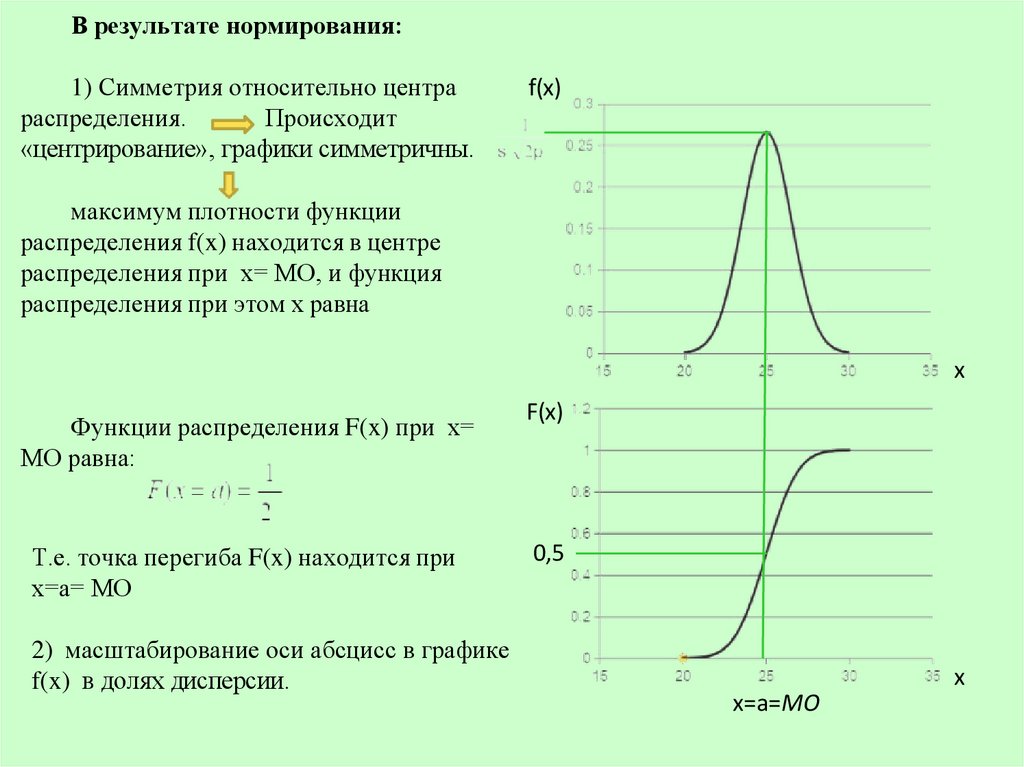
В результате нормирования:
1) Симметрия относительно центра
распределения.
Происходит
«центрирование», графики симметричны.
f(x)
максимум плотности функции
распределения f(x) находится в центре
распределения при х= МО, и функция
распределения при этом х равна
x
Функции распределения F(x) при х=
МО равна:
F(x)
Т.е. точка перегиба F(x) находится при
х=а= МО
0,5
2) масштабирование оси абсцисс в графике
f(x) в долях дисперсии.
x
x=а=МО

30.

.
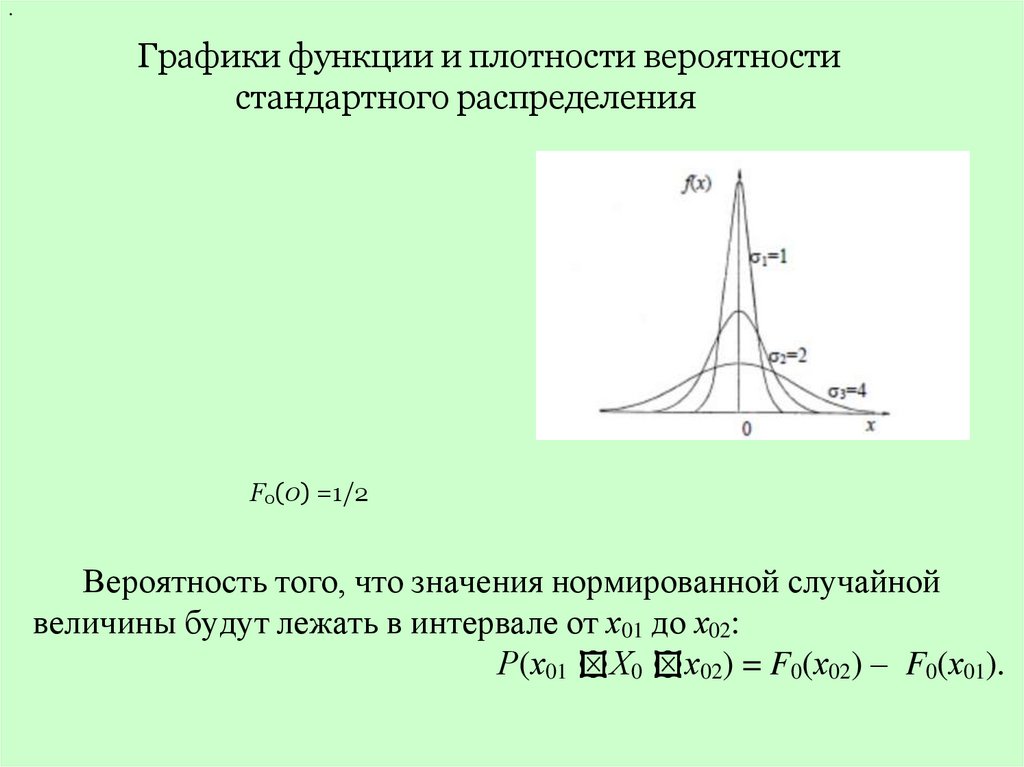
Графики функции и плотности вероятности
стандартного распределения
F0(0) =1/2
Вероятность того, что значения нормированной случайной
величины будут лежать в интервале от х01 до х02:
Р(х01 Х0 х02) = F0(х02) – F0(х01).

31.

.
Функция Лапласа:
Ф(Х) = F0(х) – ½
Значения функции Лапласа табулированы
Функция Лапласа Ф(x)
равна площади фигуры под
кривой f(x), опирающейся на
отрезок [0; x].
Φ(0) = 0;
Φ(−∞) = −0,5;
Φ(∞) = 0,5;
Φ(−x) = −Φ(x).

32.

.
Вероятность того, что значения нормированной
случайной величины будут лежать в интервале от х01 до
х02, равна:
Р(х01 Х0 х02) = F0(х02) – F0(х01)
Функция Лапласа:
F0(Х) = Ф(х) +
Ф(Х) = F0(х) – ½
½
Р(х01 Х0 х02) = F0(х02) – F0(х01) =
= Ф(х02) + ½ - Ф(х01) - ½ = Ф(х02) Ф(х01).
зная функцию Лапласа можно найти вероятность
того, что нормированная СВ Х0 попадет в тот или
иной интервал.

33.

.
Для ненормированной СВ Х:

34.

.
Задача об абсолютном отклонении
Случайная величина X распределена по нормальному
закону с параметрами m, σ. Найти вероятность того, что
случайная величина X будет принимать значения,
удаленные от математического ожидания не более чем на:
а) σ, б) 2σ, в) 3σ.

35.

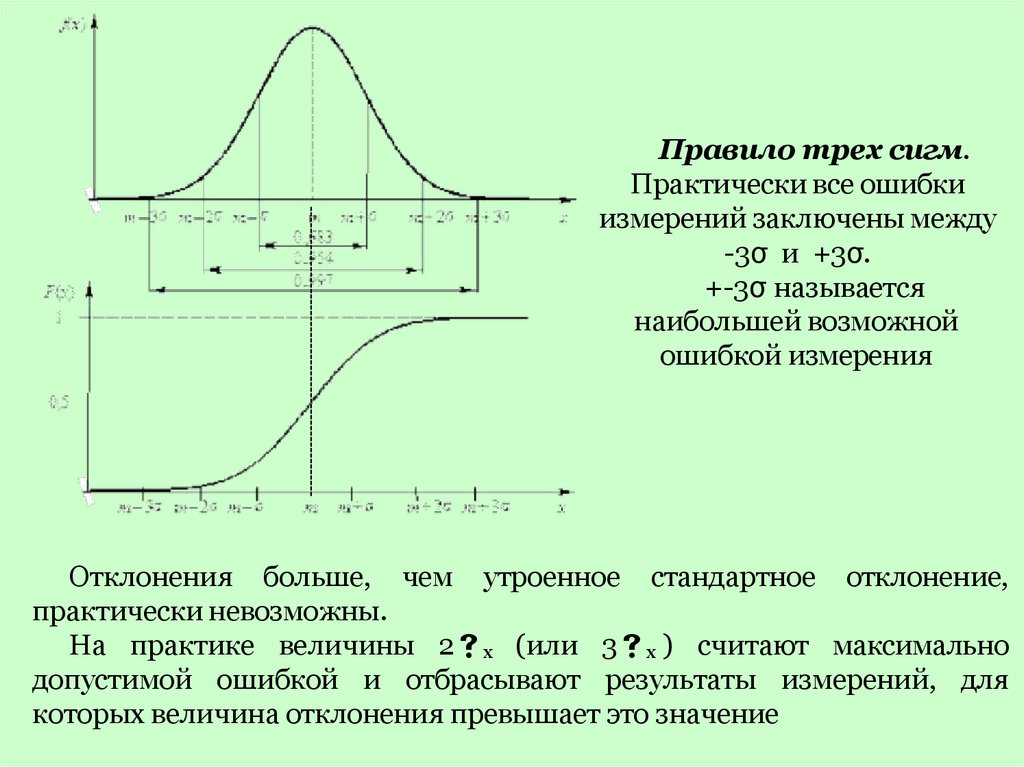
Правило трех сигм.
Практически все ошибки
измерений заключены между
-3σ и +3σ.
+-3σ называется
наибольшей возможной
ошибкой измерения
Отклонения больше, чем утроенное стандартное отклонение,
практически невозможны.
На практике величины 2 х (или 3 х ) считают максимально
допустимой ошибкой и отбрасывают результаты измерений, для
которых величина отклонения превышает это значение

36.

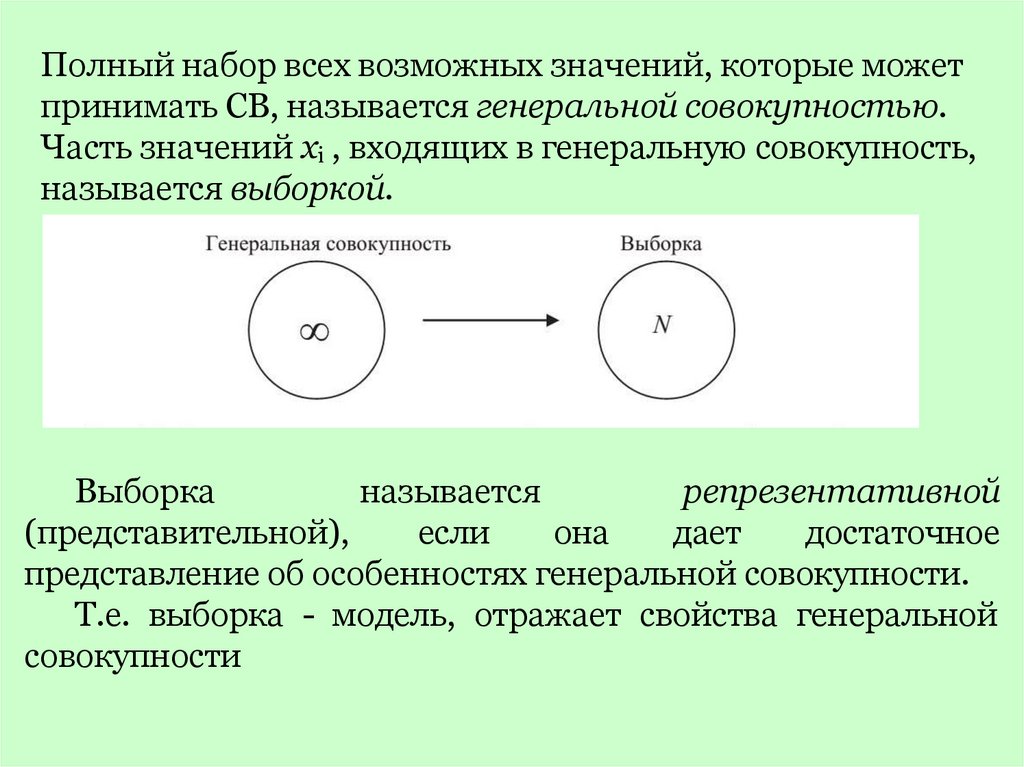
Полный набор всех возможных значений, которые может
принимать СВ, называется генеральной совокупностью.
Часть значений хi , входящих в генеральную совокупность,
называется выборкой.
Выборка
называется
репрезентативной
(представительной),
если
она
дает
достаточное
представление об особенностях генеральной совокупности.
Т.е. выборка - модель, отражает свойства генеральной
совокупности

37.

1. Оценка а* называется состоятельной, если с
увеличением объема выборки n она стремится к
оцениваемому генеральному параметру а.
Эмпирические (выборочные) моменты являются
состоятельными оценками теоретических моментов.
2.
Оценка а* называется несмещенной, если ее
математическое ожидание при любом объеме выборки
равно оцениваемому параметру а:
М [а*] = а.
3. Эффективность оценок генеральных параметров
при
фиксированном
объеме
выборок
обратно
пропорциональна дисперсиям этих оценок.
Несмещенная оценка является эффективной, если ее
дисперсия минимальна по отношению к дисперсии любой
другой оценки.

38.

Наилучшая оценкой математического ожидания для
нормально
распределенной
случайной
величины
является среднее арифметическое значение выборки
где
— среднее арифметическое выборки (серии измерений),
— сумма всех членов вариационного ряда; n— объем
выборки;

39.

.
Наилучшая несмещенная оценка генеральной дисперсии
для нормально распределенной случайной величины
является
выборочная дисперсия s2
Среднеквадратичное отклонение:

40.

Наилучшая оценкой генеральной дисперсии для
нормально распределенной случайной величины
является
выборочная дисперсия
смещенная оценка
генеральной дисперсии
НЕсмещенная оценка
генеральной дисперсии

41.

Выборочная дисперсия среднего измерений:
Выборочное среднеквадратичное отклонение
среднего измерений:
Если хотим добиться, чтобы случайная погрешность
наименьшей, нужно проводить все больше и больше опытов.
была

42.

Оценка случайной и
суммарной ошибки
косвенных
измерений

43.

ошибка косвенно измеряемой величины - это производная,
взятая в конкретной точке х= , умноженная на погрешность
Если Z = f (X), то абсолютная погрешность Z :

44.

Т.к. Δх мал, заменяем на этом участке параболу прямой
линией касательной к графику.
касательная - это первая
производная.
Z (h), м
sh

45.

Z = f (X1, X2, …, Хn).
причем величины X1, X2, …, Хn измерены
с абсолютными погрешностями Dх1, Dх2, …, Dхn
если абсолютные погрешности аргументов
независимы и случайны, то наилучшей оценкой
погрешности функции будет квадратичная сумма ее
частных производных, умноженных на
соответствующие погрешности аргументов:

46.

47.

1. Если Z – функция от одного параметZр=аf(x)
Допущение: в небольших интервалах изменения нормально
распределенного аргумента функция этого аргумента
также подчиня ется нормальн ому
закону распределения.
x1
x2
...
xn
Z=f(x)
→
z1
z2
...
zn
Если рассчитывать z трудоемко:
Серия
обрабатывается
обычным образом:
Рассчитываем
и s(Z)

48.

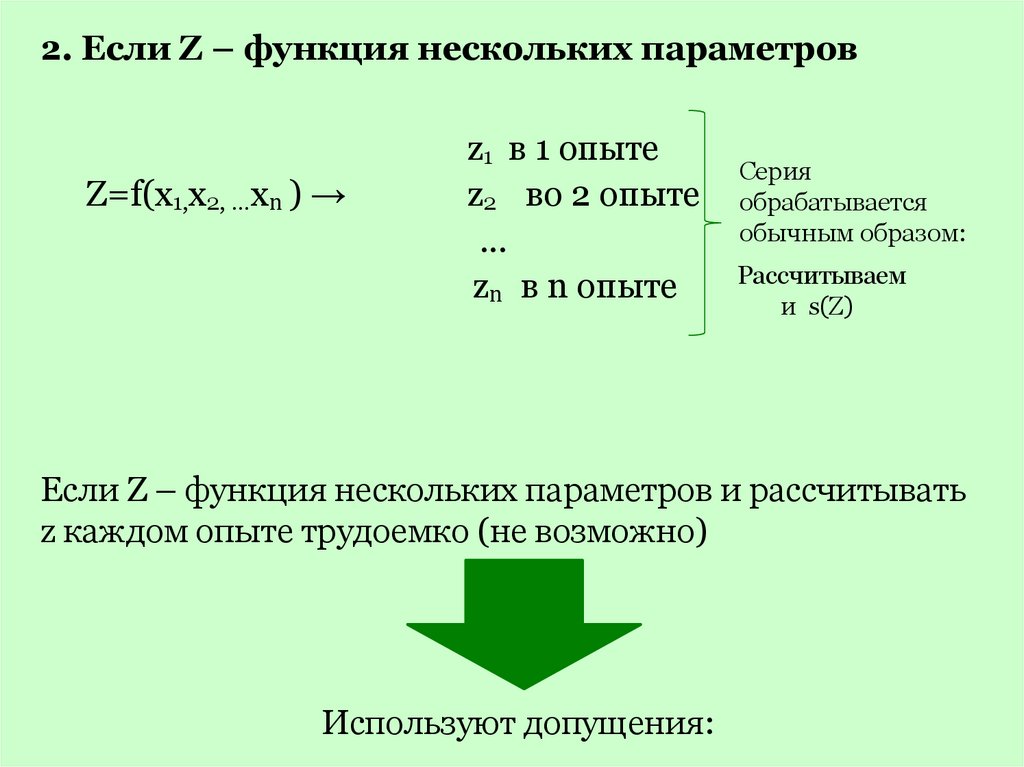
2. Если Z – функция нескольких параметров
Z=f(x1,x2, …xn ) →
z1 в 1 опыте
z2 во 2 опыте
...
zn в n опыте
Серия
обрабатывается
обычным образом:
Рассчитываем
и s(Z)
Если Z – функция нескольких параметров и рассчитывать
z каждом опыте трудоемко (не возможно)
Используют допущения:

49.

2. Если Z – функция нескольких параметров
Допущения:
1) Случайные величины X1, X2, …, Хk независимы.
2) В небольших интервалах изменения аргументов
функция Z распределена нормально.
3)
Выборочная
дисперсия
величины
равна
соответствующей генеральной
Оценка случайной ошибки функции проводится в следующем
порядке:

50.

С учетом допущений, оценка случайной ошибки
функции :
3.
1. Находим среднее функции:Величи
на
случайн
2. По закону накопления ошиобйок оцениваем выборочную
дисперсию
ошибки
:

51.

Оценка дисперсии
нормально
распределенной СВ

52.

Выборка n независимых наблюдений
распределенной случайной величиной.
Величина:
х1, х2, …, хn над нормально
имеет распределение с f = n – 1 степенями
свободы.
Плотность 2 распределения зависит только от числа степеней свободы f:
где Г(f ) — гамма-функция.
кривые плотности вероятности 2 распределения
Асимметричны,
степень асимметрии уменьшается с
увеличением f (числа опытов)
Двусторонняя доверительная оценка для
2 :

53.

оценка сверху
оценка снизу

54.

С ростом n (f) асимметрия кривых 2-распределения
уменьшается, соответственно уменьшается и асимметрия
доверительных границ.
При n 30 выборочный стандарт s (рассматриваем как
СВ, распределена нормально)
имеет математическое ожидание ms =
и ее среднеквадратичная ошибка
доверительные границы для генерального стандарта :
На прошлых лекциях оценивали МО по 1 результату измерений:

55.

Интервал I = a*
доверительный интервал
Границы интервала
a = a* -
a = a* + доверительные границы
Определение надежности оценки а* сводится к
отысканию числа εβ, позволяющего определить границу
интервала, содержащего искомую величину а с
определенной доверительной вероятностью β.
уровень значимости:

56.

1. Чем больше величина вероятности β, тем больше
доверительный интервал I (Δ)
2. При увеличении числа опытов
доверительный
интервал уменьшается при постоянной доверительной
вероятности.
Пусть β=90% =const
3. При увеличении числа опытов
доверительная
вероятность повышается при постоянной доверительном
интервале.
Пусть =const

57.

При построении доверительного интервала
решается задача об абсолютном отклонении:
Требуется найти вероятность того, что абсолютное
отклонение случайной величины не превзойдет
некоторого заданного числа :

58.

задача об абсолютном отклонении:
Итого:
Построить доверительный интервал для МО нормально
распределенной СВ с известным генеральным стандартом σ по
выборке объемом n
Знаем, что наилучшая оценка МО - среднее арифметическое
выборки.
дисперсия среднего арифметического:
Решением задачи будет:

59.

Для построения доверительного интервала нужно:
1. Задать доверительную вероятность β
2. По таблицам Функций Лапласса (приложение 1) находим
3. Затем строим доверительный интервал:
(зная σ по условию)
в общем виде
Применяем для МО
Чем больше n тем меньше доверительный интервал

60.

Построение доверительного интервала
для МО непосредственно измеряемой
величины.
Распределение Стъюдента.

61.

Построение доверительного интервала:
От случайной величины а* переходят к другой случайной
величине *, закон распределения которой не зависит от
оцениваемого параметра а, а зависит только от объема
выборки n и от вида закона распределения величины Х.
в качестве доверительных границ и обычно
используются симметричные квантили

62.

Для построения доверительного интервала при небольших
выборках
Распределение Стъюдента - это распределение среднего
арифметического по результатам n измерений (прямые
измерения), при условии, что измеряемая величина имеет
нормальное распределение

63.

При небольшом объеме выборки (n) пользуемся оценками:
- среднеарифметическим (оценка МО)
- дисперсией выборки (оценка генеральной дисперсии)
Нормальное распределение
t- распределение

64.

Плотность вероятности распределения этой величины:
где Г(f ) — гамма-функция Эйлера:
f — число степеней свободы выборки f = n – 1.

65.

66.

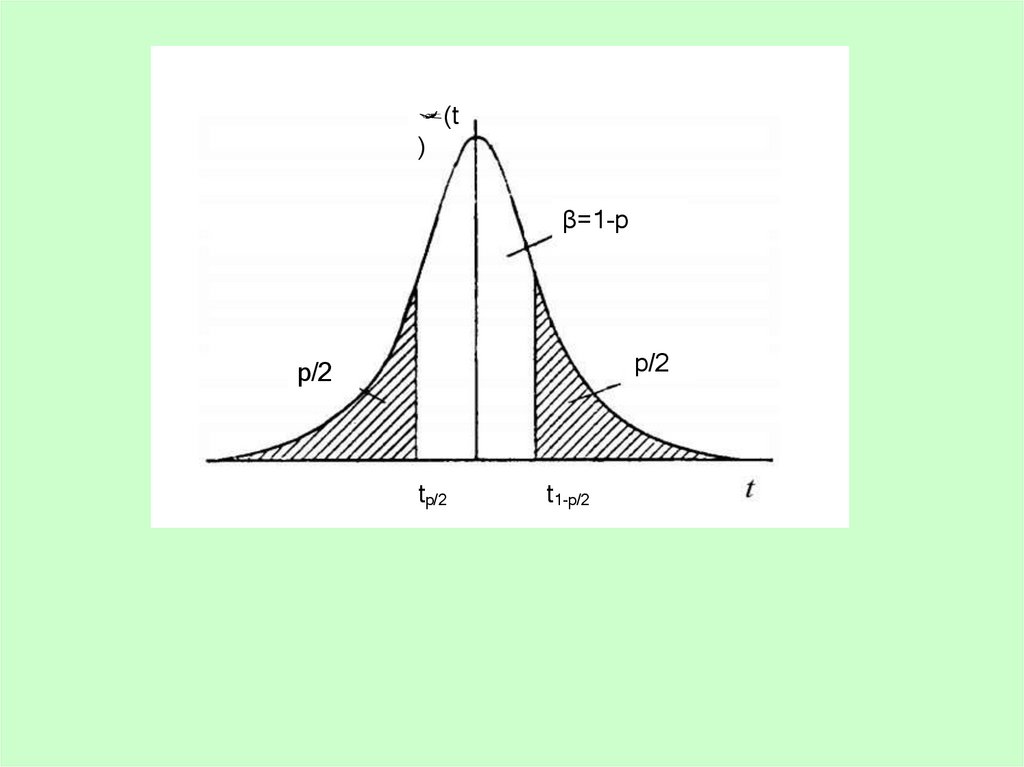
(t
)
β=1-р
p/2
p/2
tp/2
t1-p/2

67.

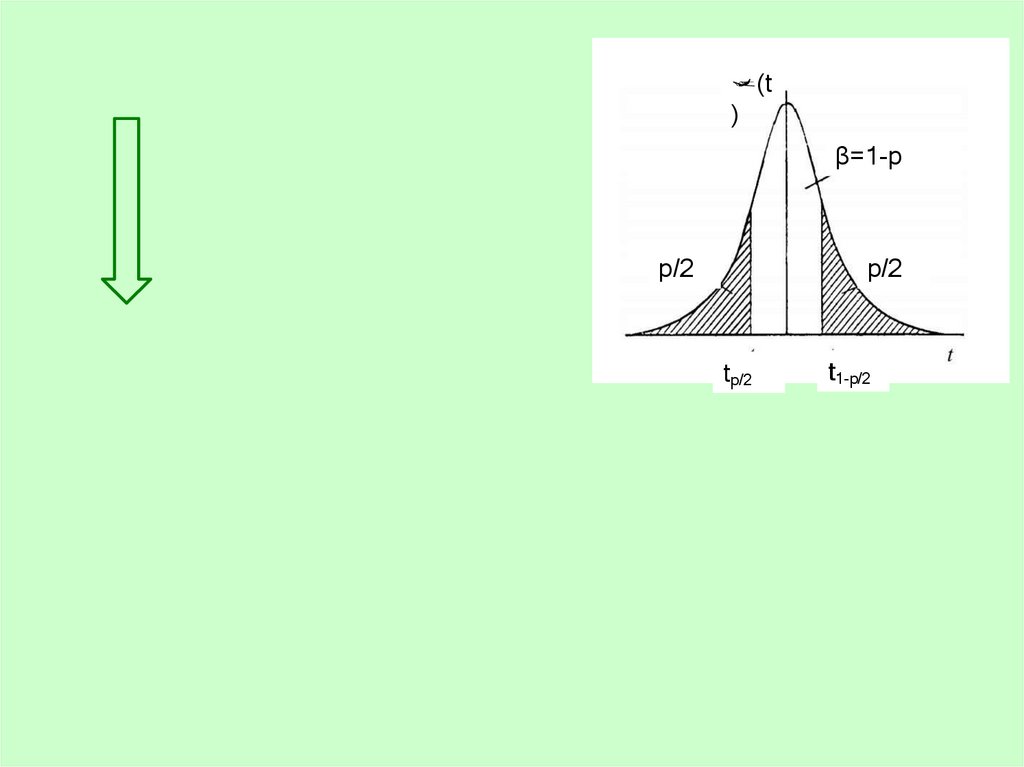
(t
)
β=1-р
p/2
p/2
tp/2
t1-p/2

68.

Проверка статистических гипотез,
критерии значимости,
ошибки первого и второго рода.

69.

Статистическая гипотеза - различного рода
предположения относительно характера или параметров
распределения случайной переменной, которые можно
проверить, опираясь на результаты наблюдений в
случайной выборке.
Выдвинутая гипотеза называется нулевой (основной).
Н0.
По отношению к высказанной (основной) гипотезе
всегда
можно
сформулировать
альтернативную
(конкурирующую), противоречащую ей - Н1.
Если принимаем Н0, то Н1 отвергаем,
Если отвергли Н0, то автоматически принимаем Н1

70.

Проверка гипотезы - сопоставление некоторых
статистических
показателей,
критериев
проверки
(критериев значимости), вычисляемых по выборке, с их
значениями, определенными в предположении, что данная
гипотеза верна.
Обычно подвергается испытанию некоторая нулевая
гипотеза Н0 в сравнении с альтернативной гипотезой Н1.
Статистический критерий – это правило (формула), по
которому определяется мера расхождения результатов
выборочного наблюдения с высказанной гипотезой Н0

71.

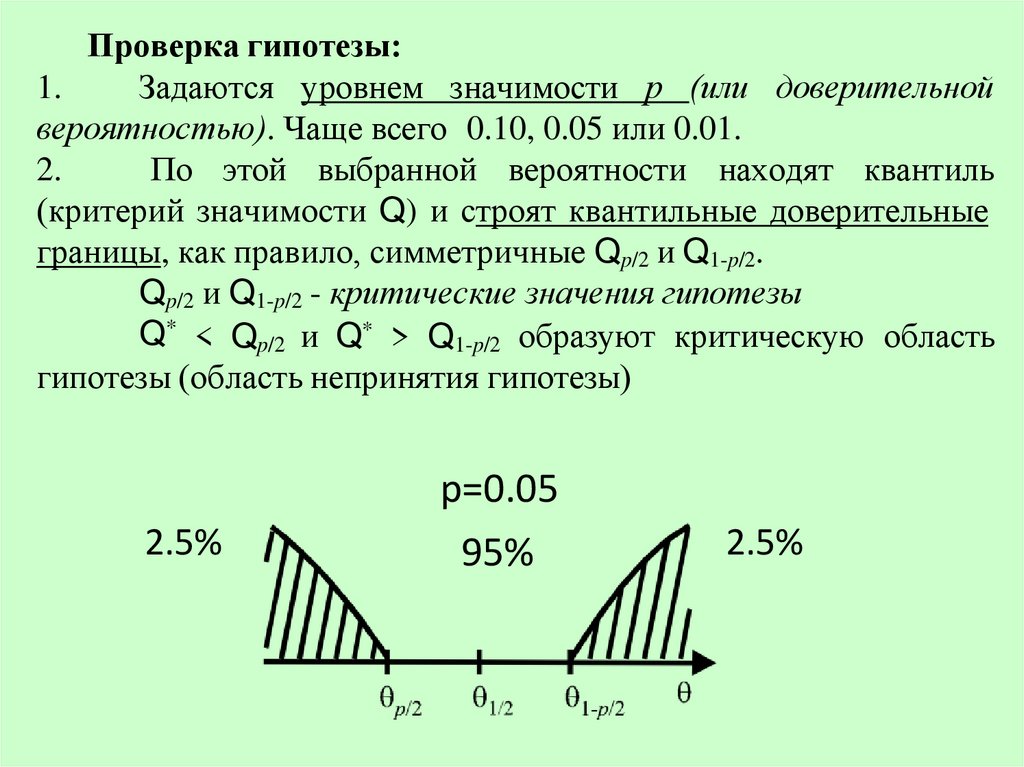
Проверка гипотезы:
1.
Задаются уровнем значимости р (или доверительной
вероятностью). Чаще всего 0.10, 0.05 или 0.01.
2.
По этой выбранной вероятности находят квантиль
(критерий значимости Q) и строят квантильные доверительные
границы, как правило, симметричные Qp/2 и Q1-p/2.
Qp/2 и Q1-p/2 - критические значения гипотезы
Q* < Qp/2 и Q* > Q1-p/2 образуют критическую область
гипотезы (область непринятия гипотезы)
2.5%
р=0.05
95%
2.5%

72.

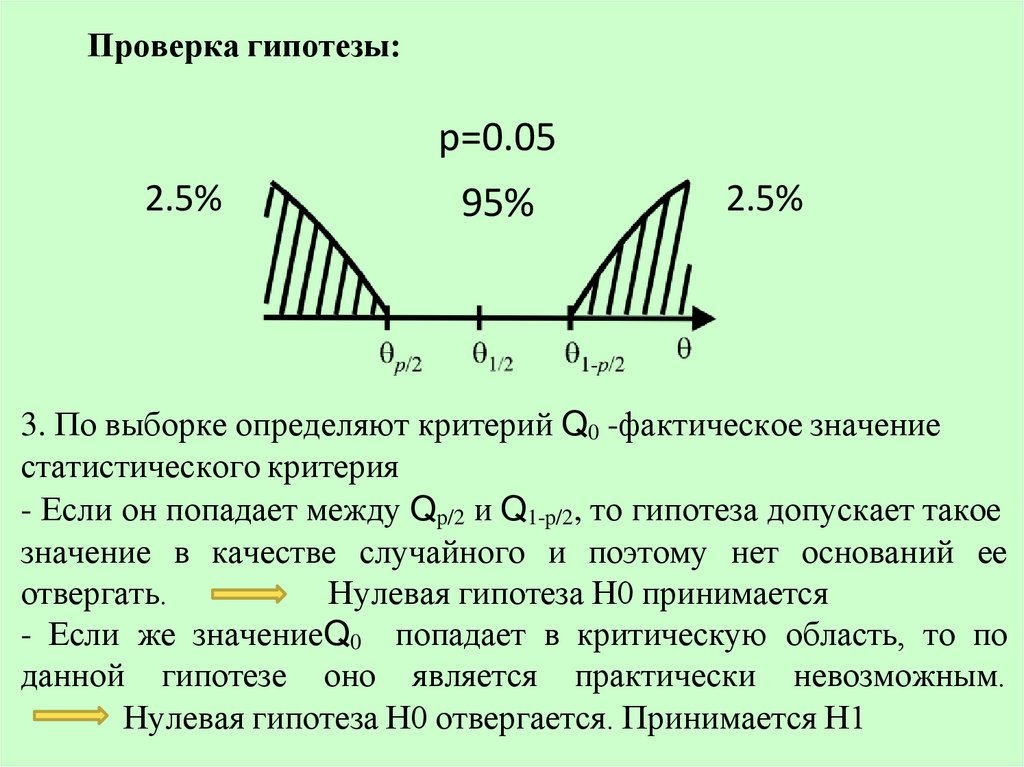
Проверка гипотезы:
р=0.05
2.5%
95%
2.5%
3. По выборке определяют критерий Q0 -фактическое значение
статистического критерия
- Если он попадает между Qp/2 и Q1-p/2, то гипотеза допускает такое
значение в качестве случайного и поэтому нет оснований ее
отвергать.
Нулевая гипотеза Н0 принимается
- Если же значениеQ0 попадает в критическую область, то по
данной гипотезе оно является практически невозможным.
Нулевая гипотеза Н0 отвергается. Принимается Н1

73.

Этапы проверки статистических гипотез:
• - выбираются испытуемая и альтернативная гипотезы;
- определяются области допустимых значений, критическая
область, а также критическое значение статистических критериев
(по соответствующим таблицам);
- вычисляется фактическое значение статистического
критерия (по выборке);
- проверяется испытуемая гипотеза на основе сравнения
фактического и критического значений критерия, и в зависимости
от результатов проверки гипотеза либо отклоняется, либо
принимается.
2.5%
р=0.05
95%
2.5%

74.

Проверка статистических гипотез осуществляется на
основании выборочных данных
(ограниченное число наблюдений)
решения относительно нулевой гипотезы Н0 имеют
вероятностный характер.
при решении о принятии или непринятии нулевой
гипотезы можно ошибиться.

75.

Ошибка первого рода - отвергается гипотеза,
которая на самом деле верна.
Вероятность ошибки равна принятому уровню
значимости
Ошибка второго рода - гипотеза принимается, а
на самом деле она неверна.
Вероятность ошибки второго рода равна ,
величина (1 - ) - мощность критерия.
Вероятность этой ошибки тем меньше, чем выше
уровень значимости p, так как при этом увеличивается
число отвергаемых гипотез.
2.5%
р=0.05
95%
2.5%

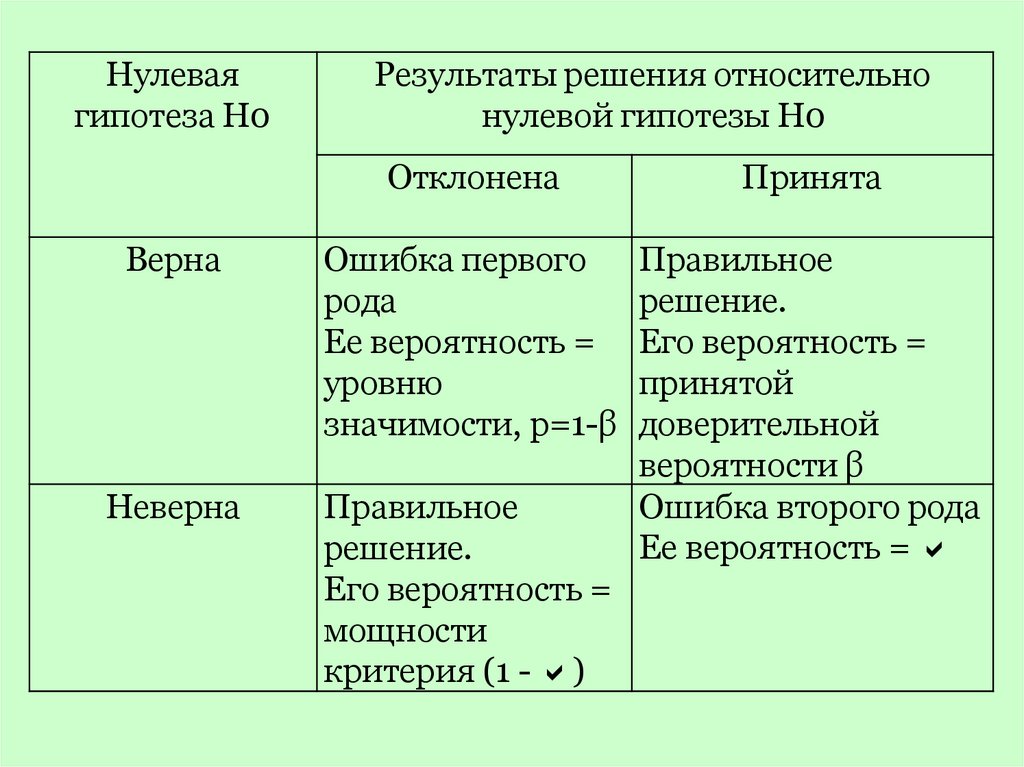
76.

Нулевая
гипотеза Н0
Результаты решения относительно
нулевой гипотезы Н0
Отклонена
Верна
Неверна
Принята
Ошибка первого
Правильное
рода
решение.
Ее вероятность = Его вероятность =
уровню
принятой
значимости, р=1-β доверительной
вероятности β
Правильное
Ошибка второго рода
Ее вероятность =
решение.
Его вероятность =
мощности
критерия (1 - )

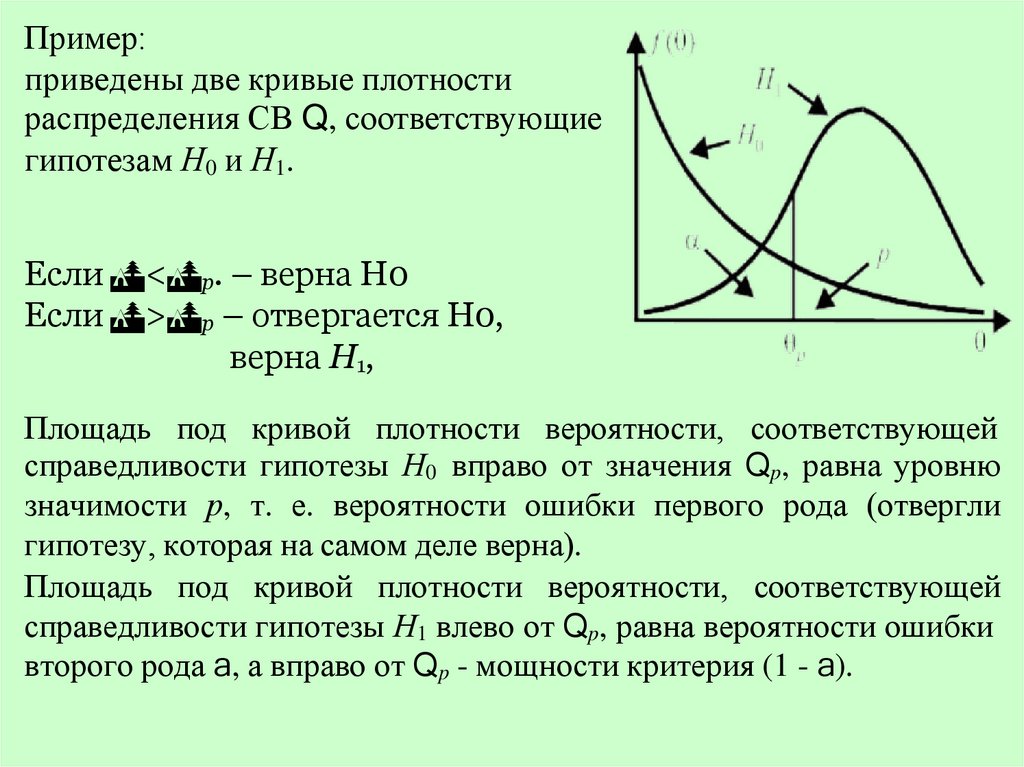
77.

Пример:
приведены две кривые плотности
распределения СВ Q, соответствующие
гипотезам Н0 и Н1.
Если < p. – верна Н0
Если > p – отвергается Н0,
верна Н1,
Площадь под кривой плотности вероятности, соответствующей
справедливости гипотезы Н0 вправо от значения Qp, равна уровню
значимости р, т. е. вероятности ошибки первого рода (отвергли
гипотезу, которая на самом деле верна).
Площадь под кривой плотности вероятности, соответствующей
справедливости гипотезы Н1 влево от Qp, равна вероятности ошибки
второго рода a, а вправо от Qp - мощности критерия (1 - a).

78.

При проверке гипотезы стремятся из всех
возможных критериев выбрать тот, у которого
при заданном уровне значимости меньше
вероятность ошибки второго рода.

79.

Найдены два значения а1* и а2* некоторого генерального
параметра а
Н0: а1*= а2*.
Н1: а1* > а2*
а1* < а2*.
Критерий
или
Вычисляем фактическое
Сопоставляем с 0 (или 1). Делаем выводы.
Если одно из этих равенств заведомо невозможно, то
альтернативная гипотеза называется односторонней, и для
ее
проверки
применяют односторонние
критерии
значимости (в отличие от обычных, двусторонних). При
этом необходимо рассматривать лишь одну из половин
критической области.

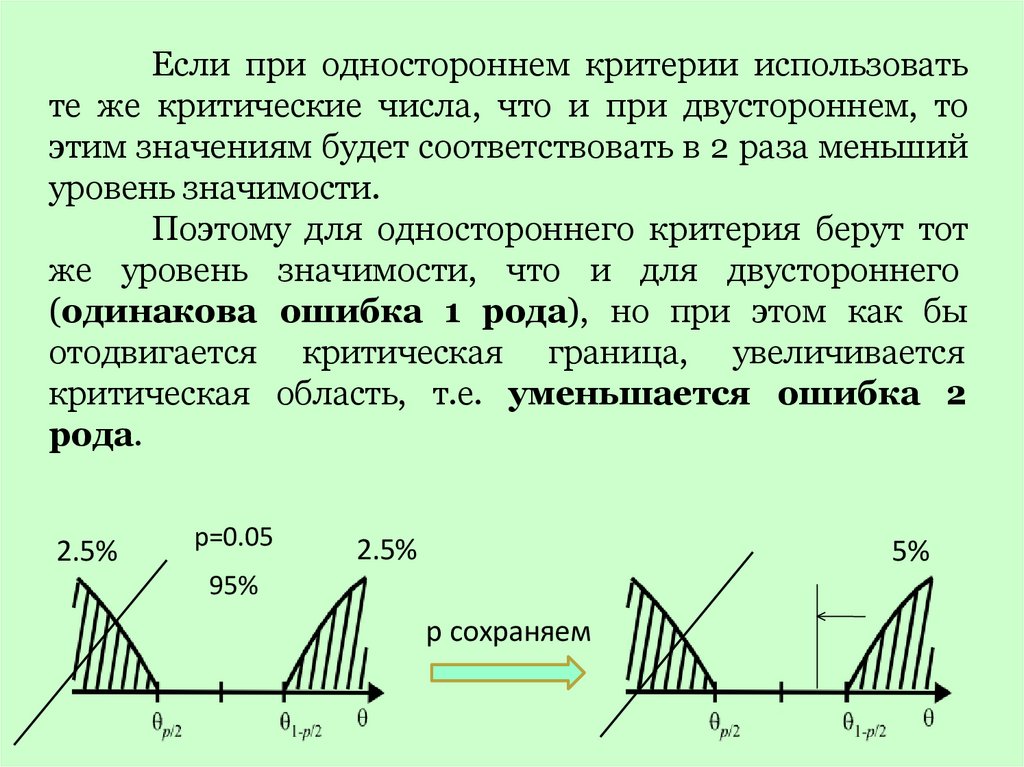
80.

Если при одностороннем критерии использовать
те же критические числа, что и при двустороннем, то
этим значениям будет соответствовать в 2 раза меньший
уровень значимости.
Поэтому для одностороннего критерия берут тот
же уровень значимости, что и для двустороннего
(одинакова ошибка 1 рода), но при этом как бы
отодвигается критическая граница, увеличивается
критическая область, т.е. уменьшается ошибка 2
рода.
2.5%
р=0.05
2.5%
5%
95%
p сохраняем

81.

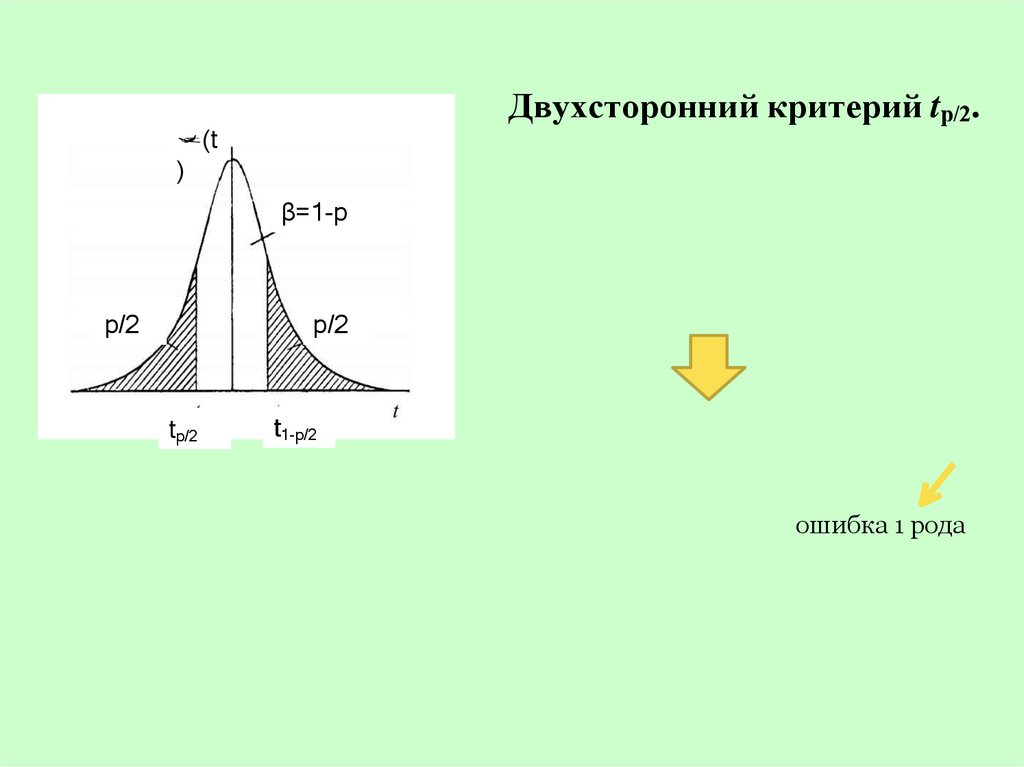
Двухсторонний критерий tр/2.
(t
)
β=1-р
p/2
p/2
tp/2
t1-p/2
ошибка 1 рода

82.

Односторонний критерий tр.
(t
)
β=1-р
p/2
p/2
tp/2
t1-p/2
не может быть по условию
ошибка 1 рода
Хотим сохранить!
Односторонний критерий tp при уровне значимости р численно
равен двухстороннему tр/2, но при уровне значимости р/2 (для
одного и того же числа степеней свободы f = n – 1)
tp(односторонний) должен равняться двустороннему - tp/2 (при этом уровень
значимости двустороннего в 2 раза больше).
пример: tp с выбранным р=0,05 (tp=0,05) должен равняться двустороннему - tp/2, у
которого р=0,1 ( tp/2=0.1/2=0.05=tp=0,05)

83.

Проверка однородности
результатов измерений

84.

Наличие грубой ошибки в выборке нарушает характер
распределения случайной величины, т.е. нарушается
однородность наблюдений. Следовательно, выявление
грубых ошибок (промахов) можно трактовать как проверку
однородности наблюдений, т. е. проверку гипотезы о том,
что все элементы выборки получены из одной и той же
генеральной совокупности.
Пусть имеется выборка х1, х2, х3…хn значений нормально
распределенной СВ
Н0: все элементы выборки принадлежат генеральной
совокупности
Н1: часть элементов выборки принадлежат другой
генеральной совокупности

85.

Величины:
хmax (хmin) наибольший (наименьший) результат измерений.
( ) имеют специальное распределение, зависящее только
от числа степеней свободы f = n – 2
Критерий : табл при f=n-2 (табл.7, стр
66)
Условие:
- Н0 принимается, хmax (хmin) НЕ исключается из
выборки как грубое измерение
- Н0 отвергается, хmax (хmin) исключается из
выборки

86.

Если сомнение вызывают два или три элемента выборки:
- для всех сомнительных элементов вычисляют ( ).
- исследование начинается с элемента, имеющего наименьшее
значение ( ), при этом остальные сомнительные элементы
из выборки исключаются.
- для этой уменьшенной выборки вычисляют среднее значение,
среднеквадратичное отклонение и новое значение ( ) для
исследуемого элемента.
- если исследуемый элемент является грубым измерением, то
ВСЕ сомнительные элементы исключаются из выборки.
- если исследуемый элемент не является грубым измерением,
его присоединяют к выборке и начинают исследовать
следующий по величине ( ) элемент выборки

87.

Имеется выборка
х1, х2, х3, х4, х5, х6
хmax
n=6
хmin
Рассчитываем
и s
Для х2 -
для х6 -
Допустим, что =2.1 (для х2) , =1.7 (для х6)
( )
ее
Начинаем проверку для х6. х2 из выборнкаииумбеинрьаш
ем
Рассматриваем: х1, х3, х4, х5, х6
Рассчитываем
n=5
и s и для х6
Сравниваем с табл

88.

Вариант 1.
> табл
х6 – промах, грубая ошибка (и х2 тоже).
Переходим к выборке: х1, х3, х4, х5 n=4
Вариант 2.
< табл
выборке
х6 –не грубая ошибка, остается в
Проверяем х2

89.

Сравнение двух дисперсий.
Распределение Фишера

90.

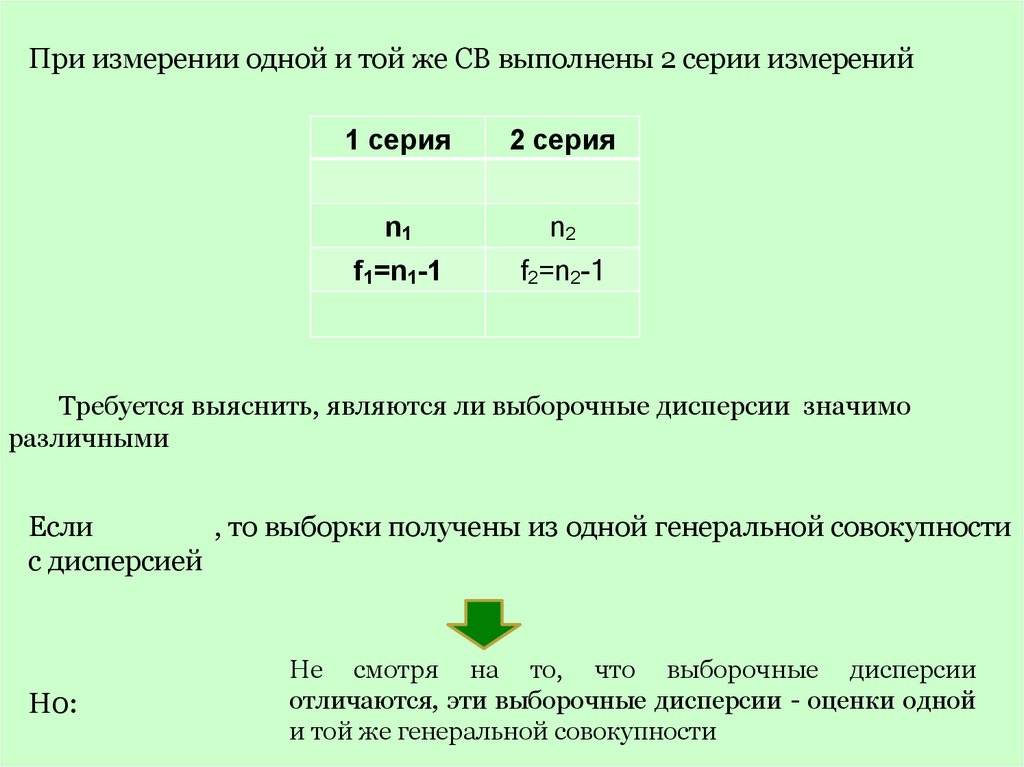
При измерении одной и той же СВ выполнены 2 серии измерений
1 серия
2 серия
n1
n2
f1=n1-1
f2=n2-1
Требуется выяснить, являются ли выборочные дисперсии значимо
различными
Если
, то выборки получены из одной генеральной совокупности
с дисперсией
Н0:
Не смотря на то, что выборочные дисперсии
отличаются, эти выборочные дисперсии - оценки одной
и той же генеральной совокупности

91.

Н0:
Н1:
≠
Если нулевая гипотеза будет принята
выборочные дисперсии называются
ОДНОРОДНЫМИ.
(Различие между ними незначительно и
обусловлено влиянием случайных факторов)
Если нулевая гипотеза отвергается
дисперсии НЕОДНОРОДНЫ
(различие между ними значимо)
Итак, чтобы отвергнуть нулевую гипотезу, нужно доказать
значимость различия между выборочными дисперсиями при
выбранном уровне значимости р
Критерий значимости - критерий
Фишера.

92.

Распределением Фишера (F-распределением) обладает случайная
величина:
Плотность F-распределения зависит только от f1 и f2:
Кривые асимметричны.
Критерий Фишера - односторонний

93.

При
выбранной
доверительной
вероятности
значимости р) двусторонняя оценка величины F
Но в условии нулевой гипотезы
(уровне

94.

Для удобства и перехода к одностороннему критерию Фишера
принято, что за
всегда обозначается большая дисперсия
Левое неравенство выполняется ВСЕГДА

95.

Тогда Условие однородности дисперсий:
нулевая гипотеза принята
выборочные дисперсии ОДНОРОДНЫ.
нулевая гипотеза отвергается.
выборочные дисперсии НЕОДНОРОДНЫ.

96.

Пример.
При определении сопротивления раствора в двух сериях опытов
получены:
1 серия
2 серия
n1=4
n2=12
f1=n1-1
f2=n2-1
Можно ли считать выборочные дисперсии однородными?
что за
всегда обозначается большая дисперсия
нулевая гипотеза
дисперсии однородны
принимается,

97.

Определение дисперсии
по текущим измерениям.
Сравнение нескольких
дисперсий

98.

Дисперсия
сходимости
–
выборочная
дисперсия, полученная по результатам одной серии
опытов.
Дисперсия воспроизводимости – дисперсия,
характеризующая 2 и более серии опытов
ошибка воспроизводимости

99.

1 серия
2 серия
3 серия
…
k серия
1 образец
2 образец
3 образец
…
k образец
…
n1
n2
f1=n1-1
f2=n2-1
n3
f3=n3-1
…
…
nk
fk=nk-1
…
ВАЖНО!!! При вычислении дисперсии воспроизводимости по
текущим измерениям можно объединять между собой только те
результаты, которые можно рассматривать как выборки из
генеральных совокупностей с равными дисперсиями, т.е. все
частные дисперсии должны быть ОДНОРОДНЫМИ.

100.

Если число опытов для каждого образца одинаково
(n1 = n2 = … = nk = n):
т. е. при равном числе параллельных опытов общая
дисперсия воспроизводимости равна
среднеарифметическому значению частных дисперсий.
Число степеней свободы равно fвоспр. = k (n - 1).

101.

критерий БАРТЛЕТА
Принимается
нулевая
гипотеза
о
соответствующих генеральных дисперсий.
Н0:
равенстве
В условиях нулевой гипотезы отношение В/С
распределено приближенно как 2 с (k – 1) степенями
свободы, если все fj > 2
Если при выбранном уровне
значимости
Н0 принимается, различие между
выборочными
дисперсиями
незначимо, а сами выборочные
дисперсии — однородны

102.

критерий БАРТЛЕТА
Н0 принимается, различие между
выборочными
дисперсиями
незначимо, а сами выборочные
дисперсии — однородны
Так как всегда С > 1, то
Если
Если
Н0 принимаем, дисперсии
однородны
критерий Бартлета
вычислить полностью.
нужно

103.

критерий БАРТЛЕТА
ПРИМЕР
Пусть сделано 3 серии: k=3
Проверить дисперсии на однородность по критерию Бартлета

104.

критерий БАРТЛЕТА
ПРИМЕР
Пусть сделано 3 серии: k=3
Проверить дисперсии на однородность по критерию Бартлета
χ2
1-р для р=0,05 и числа степеней свободы f=k-1=3-1=2 равен 6
Гипотеза принимается.
Дисперсии однородны

105.

критерий КОХРЕНА
в случае выборок одинакового объема (n1=n2=…=nk=n)
Распределение случайной величины G зависит только от
числа суммируемых частных дисперсий k и числа
степеней свободы f = n – 1, с которым определена каждая
дисперсия
Н0 принимается, различие между
выборочными
дисперсиями
незначимо, а сами выборочные
дисперсии — однородны

106.

критерий КОХРЕНА
ПРИМЕР
Пусть сделано 3 серии: k=3
Проверить дисперсии на однородность по критерию Кохрена
Дисперсии однородны

107.

Сравнение двух средних.
Расчет
средневзвешенного
значения

108.

1 серия
n1
2 серия
n2
Получены из генеральных совокупностей с параметрами:
2
m1, σ1
2
m2, σ2
Оценками соответствующих генеральных параметров являются:
,
,
ЗАДАЧА сопоставить результаты измерений
наилучшую оценку искомой величины
и дать
1. Сопоставляем дисперсии, т.е. проверяем выборочные
дисперсии на однородность
однородны
неоднородны

109.

2. Сопоставляем средние значения
1 вариант:
Дисперсии однородны
2 вариант:
Дисперсии неоднородны
1 вариант: выборочные дисперсии однородны, т.е.
являются оценками одной и той же генеральной
совокупности
Нулевая гипотеза Но: m1=m2=m
т.е. оценки наилучшего значения СВ (х1 и х2) – являются
оценками одного и того же математического ожидания.
Условием является: m1-m2=0
Нужно построить доверительный интервал для величины z
=m1-m2 используя критерий Стъюдента

110.

Величина z будет распределена нормально с параметрами:
Составим нормированную случайную величину z0:
переходим к величине t с
распределением Стъюдента
(f =n1+n2–2) (заменяем
генеральный стандарт
выборочным)
Где

111.

Доверительные границы для t
или
Если ноль содержится внутри доверительного интервала
для m1 – m2, нулевая гипотеза о том, что средние х1 и х2
являются оценками одного и того же МО принимается.

112.

В условиях нулевой гипотезы m1 = m2
Тогда можно вывести следующий критерий проверки
нулевой гипотезы.
Н0 принимается, если:
В том случае если выборочные средние
являются оценками одного и того же
математического ожидания и выборочные
дисперсии однородны, то полученные
выборки можно объединить в одну серию и
рассчитать для нее общие среднее и
дисперсию.

113.

2 вариант: выборочные дисперсии неоднородны, т.е. их
нельзя объединить в дисперсию воспроизводимости
Нулевая гипотеза Но: m1=m2=m
т.е. оценки наилучшего значения СВ (х1 и х2) – являются
оценками одного и того же математического ожидания.
Критерий проверки:
Нулевая гипотеза принимается, если

114.

Если выборочные средние оценивают одно и то же
математическое ожидание, то в качестве единственной
наилучшей оценки обычно используется средневзвешенное
значение.
Статистический вес результата, полученного в каждой
серии опытов:
Средневзвешенное значение (наилучшая оценка для Х):

115.

Если выборочные средние НЕ оценивают одно и то же
математическое ожидание, то в качестве оценки
используется средневзвешенное значение.
НО: в качестве погрешностей средних значений следует
брать суммарные ошибки
Статистический вес результата, полученного в каждой
серии опытов:
Средневзвешенное значение (наилучшая оценка для Х):

116.

ЗАДАЧА
В разных лабораториях независимо друг от друга проводились
измерения некоторой физико-химической величины.
Сопоставить результаты двух лабораторий
При необходимости принять систематическую ошибку 0.1% для
двух лабораторий
Доверительная вероятность 95%
Лаборатория 1
253,22
252,48
252,02
253,46
253,45
251,42
Лаборатория 2
251,36
251,98
251,43
252,37

117.

ЗАДАЧА
План решения.
1. Проверяем на однородность каждую серию измерений.
Находим наилучшее значение и погрешность для каждой
серии.
2. Сопоставляем результаты двух серий
1.
Проверяем на однородность дисперсии по критерию
Фишера
2. Сопоставляем средние.
3. Делаем выводы и определяем наилучшее значение
и погрешность двух серий измерений

118.

ЗАДАЧА
1 шаг.
Находим для каждой лаборатории среднее значение, дисперсию и
среднеквадратичное отклонение.
Проверка на однородность:
Н0: все элементы выборки принадлежат одной генеральной совокупности
Н1: часть элементов выборки не принадлежит генеральной совокупности
Находим ( ) для максимального и минимального значений выборки
Проверяем на грубую ошибку х, который наиболее отличается от среднего
значения (для которого ( ) максимальный).
Сравниваем с табличным значением.
табл ( f = n – 2; р=0,05).
Если
, то проверяемый х не является грубым промахом, его
нужно оставить в выборке. Н0 принимаем.
Если
, то проверяемый х необходимо исключить из выборки,
перейти к новой выборке и проверку на однородность повторить, пока Н0 не
будет принята.

119.

ЗАДАЧА
1 шаг.
Критерий : табл при f=n-2 (табл.7, стр
66)
Условие:
- Н0 принимается, хmax (хmin) НЕ исключается из
выборки как грубое измерение
- Н0 отвергается, хmax (хmin) исключается из
выборки

120.

ЗАДАЧА
2 шаг.
1. Проверяем на однородность дисперсии по критерию Фишера
Н0:
Выборочные дисперсии - оценки одной и той же генеральной совокупности
(однородны). Различие между ними незначительно и обусловлено влиянием
случайных факторов.
Н1:
За s1 всегда обозначается большая дисперсия!!!
Условие однородности дисперсий (принятие Н0):

121.

2 шаг. 2.2 Сопоставляем средние.
Н0: m1=m2=m
т.е. оценки наилучшего значения СВ (х1 и х2) – являются оценками
одного и того же математического ожидания.
Н1: m1≠m2≠m
1 вариант.
Дисперсии выборочные однородны – можно объединить в дисперсию
воспроизводимости
Нулевая гипотеза принимается, если
выборочные
дисперсии среднего
(ошибка опыта):
Критерий Стъюдента берем для числа степеней свободы fвоспр = f1+f2
2 вариант.
Дисперсии выборочные НЕоднородны – их нельзя объединить в дисперсию
воспроизводимости
Нулевая гипотеза принимается, если

122.

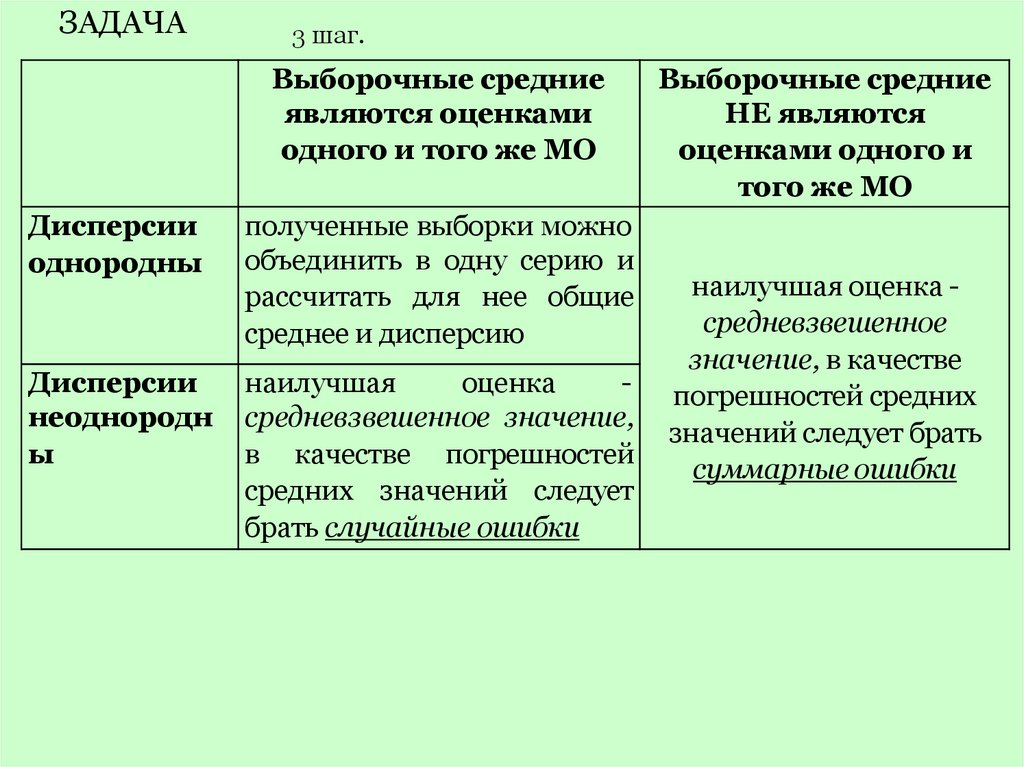
ЗАДАЧА
3 шаг.
Выборочные средние
являются оценками
одного и того же МО
Дисперсии
однородны
полученные выборки можно
объединить в одну серию и
рассчитать для нее общие
среднее и дисперсию
Дисперсии
неоднородн
ы
наилучшая
оценка
средневзвешенное значение,
в качестве погрешностей
средних значений следует
брать случайные ошибки
Выборочные средние
НЕ являются
оценками одного и
того же МО
наилучшая оценка средневзвешенное
значение, в качестве
погрешностей средних
значений следует брать
суммарные ошибки