Classical Cryptography

1. Classical Cryptography

2. What is cryptography?

• kryptos – “hidden”
• grafo – “write”
• Keeping messages secret
• Usually by making the message unintelligible to anyone that intercepts
it

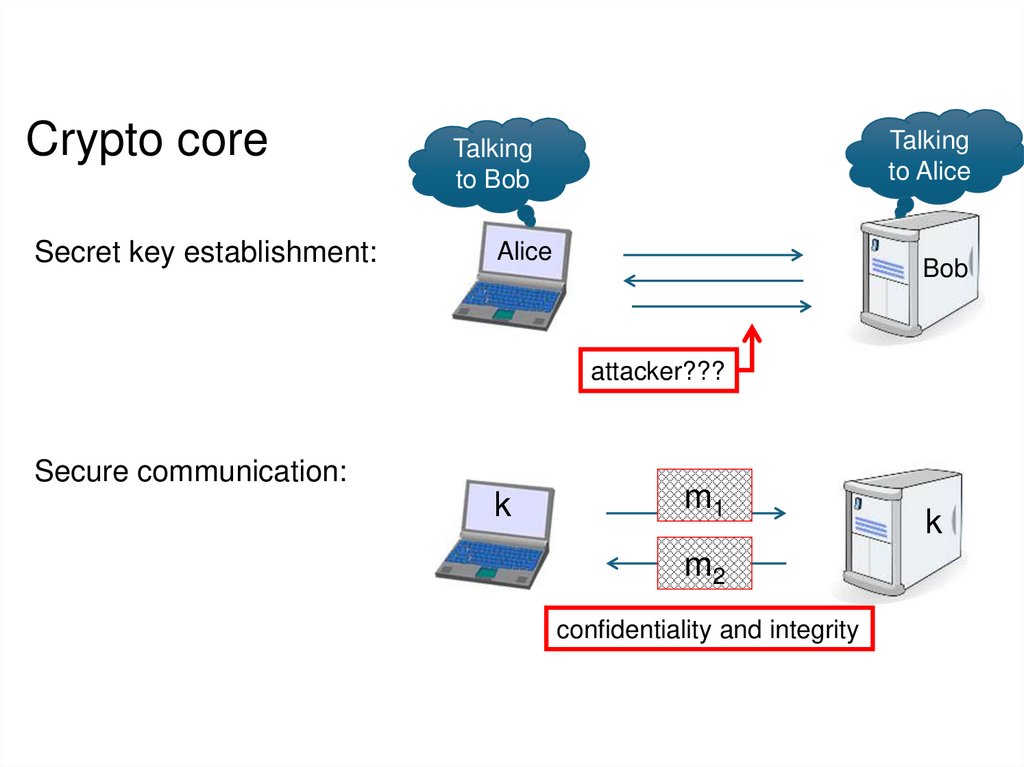
3. Crypto core

Secret key establishment:
Talking
to Alice
Talking
to Bob
Alice
Bob
attacker???
Secure communication:
k
m1
m2
confidentiality and integrity
k

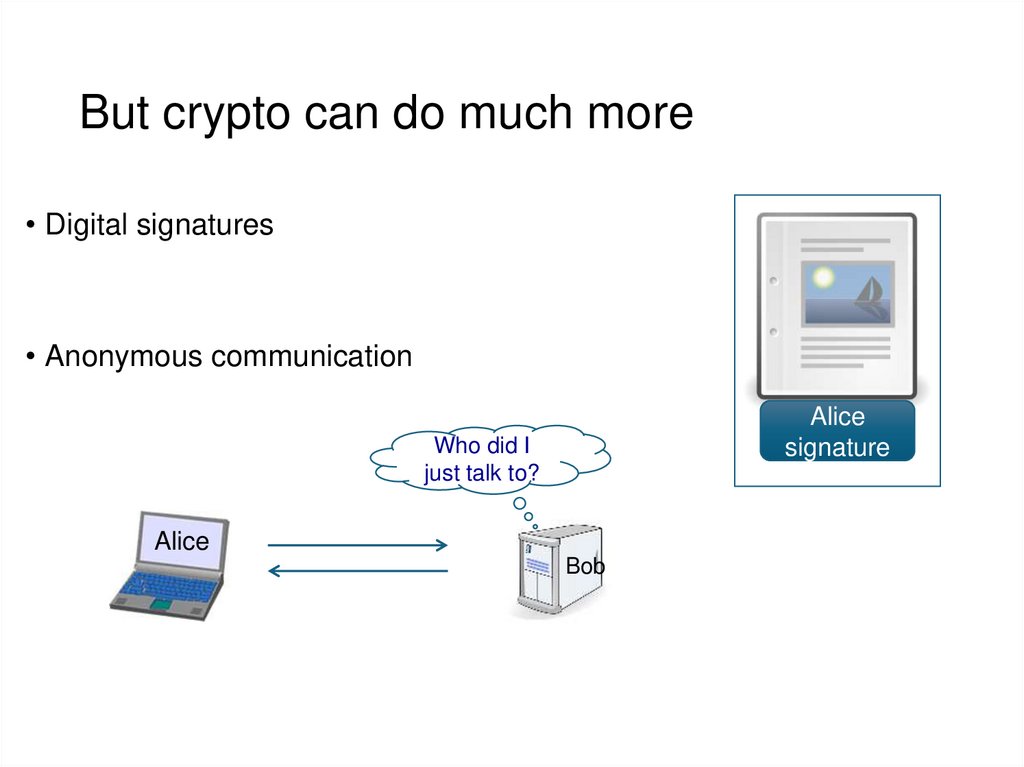
4. But crypto can do much more

• Digital signatures
• Anonymous communication
Alice
signature
Who did I
just talk to?
Alice
Bob

5. But crypto can do much more

• Digital signatures
• Anonymous communication
• Anonymous digital cash
• Can I spend a “digital coin” without anyone knowing who I am?
• How to prevent double spending?
1$
Alice
Internet
(anon. comm.)
Who
was
that?

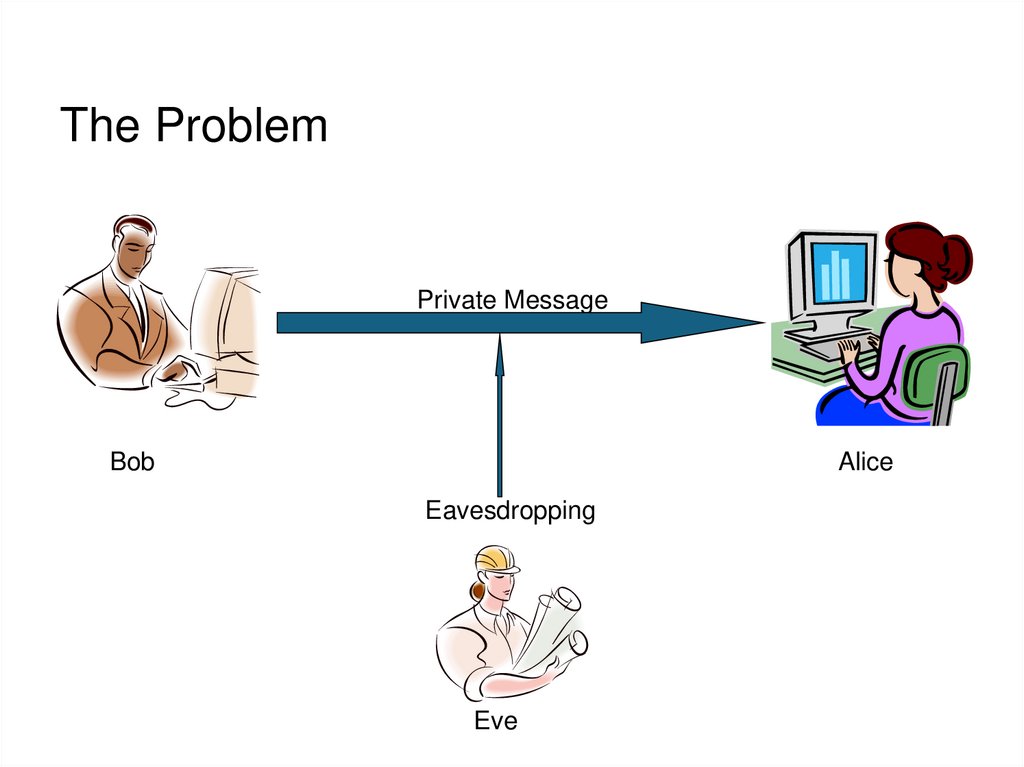
6. The Problem

Private Message
Bob
Alice
Eavesdropping
Eve

7. The Solution

Private Message
Private Message
Encryption
Decryption
Scrambled Message
Bob
Alice
Eavesdropping
Eve

8. What do we need?

• Bob and Alice want to be able to encrypt/decrypt easily
• But no one else should be able to decrypt
• How do we do this?
• Keys!

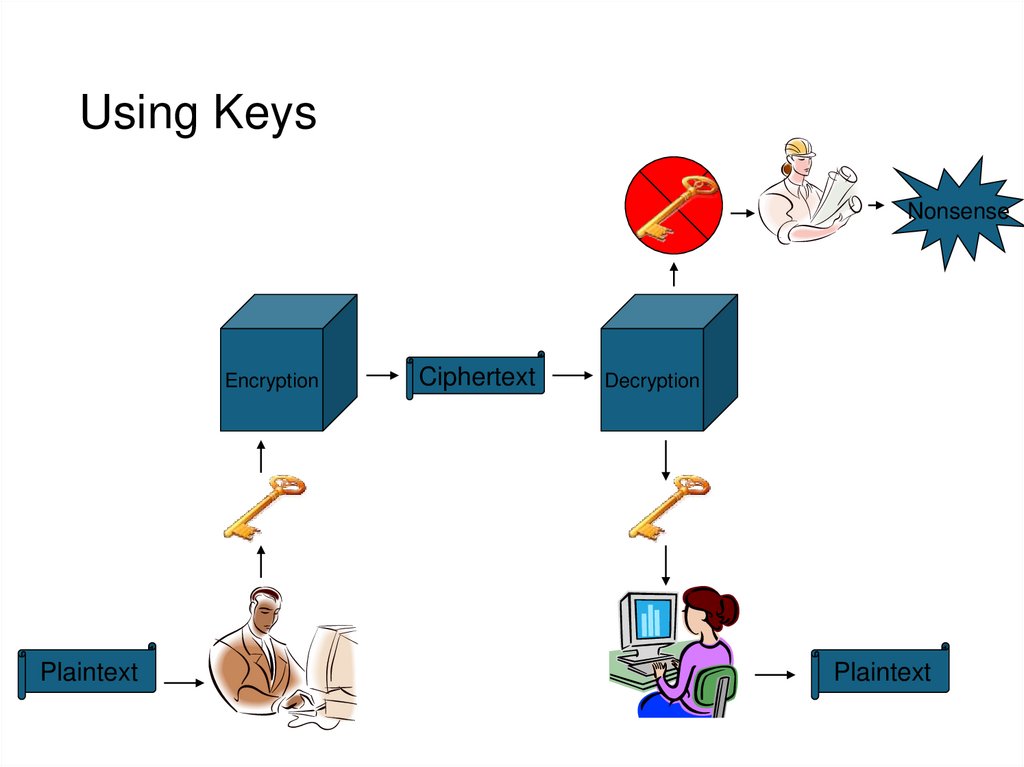
9. Using Keys

Nonsense
Encryption
Plaintext
Ciphertext
Decryption
Plaintext

10. What is a cipher?

• A cipher is an algorithm for encryption/decryption
• Kerckhoff’s Principle: All details of the cipher should be public
• Eve still shouldn’t be able to decrypt messages unless she has the
secret key

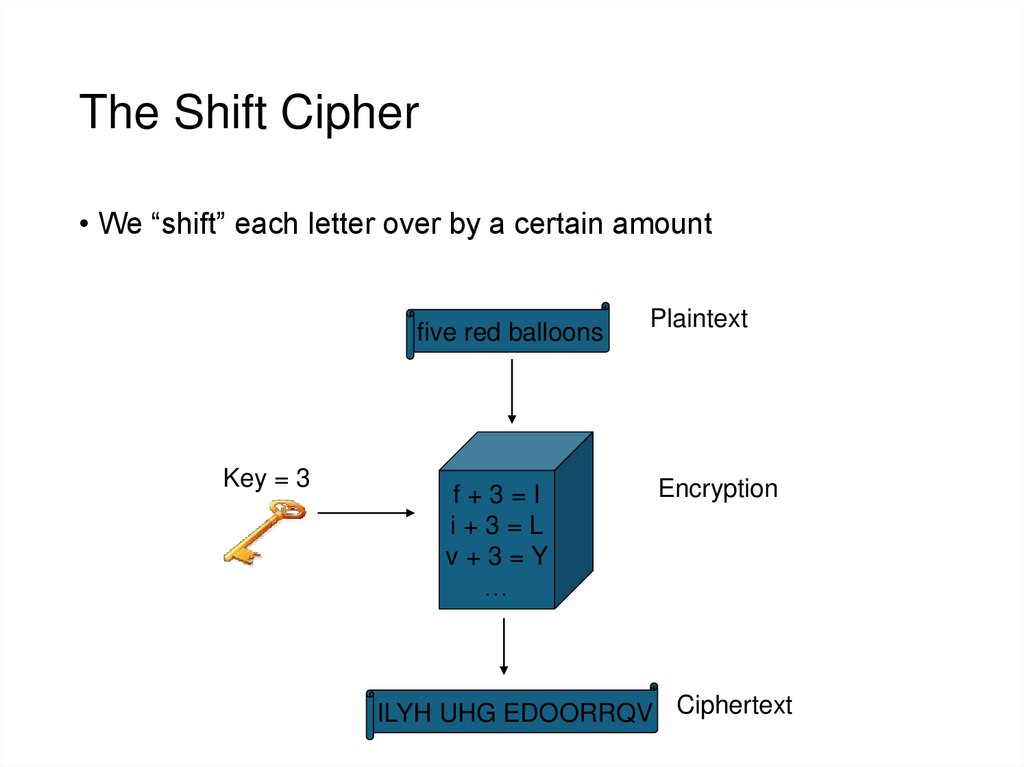
11. The Shift Cipher

• We “shift” each letter over by a certain amount
five red balloons
Key = 3
f+3=I
i+3=L
v+3=Y
…
Plaintext
Encryption
ILYH UHG EDOORRQV Ciphertext

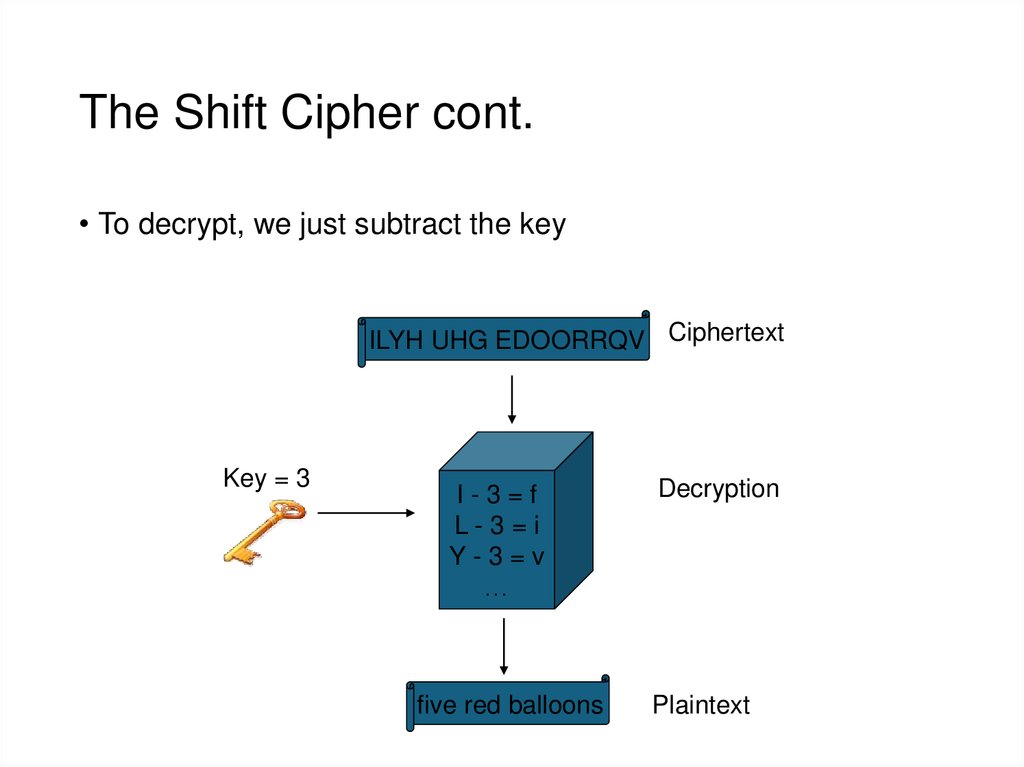
12. The Shift Cipher cont.

• To decrypt, we just subtract the key
ILYH UHG EDOORRQV Ciphertext
Key = 3
I-3=f
L-3=i
Y-3=v
…
Decryption
five red balloons
Plaintext

13. What’s wrong with the shift cipher?

• Not enough keys!
• If we shift a letter 26 times, we get the same letter back
• A shift of 27 is the same as a shift of 1, etc.
• So we only have 25 keys (1 to 25)
• Eve just tries every key until she finds the right one

14. The Substitution Cipher

• Rather than having a
fixed shift, change
every plaintext letter to
an arbitrary ciphertext
letter
Plaintext
a
b
c
d
e
…
z
Ciphertext
G
X
N
S
D
…
Q

15. The Substitution Cipher cont.

a
G
n
B
b
X
o
Y
c
N
p
Z
d
S
q
P
Key = e
D
r
H
f
A
s
W
g
F
t
I
h
V
u
J
i
L
v
R
j
M
w
U
k
C
x
K
l
O
y
T
m
E
z
Q
five red balloons
f =A
i =L
v =R
…
Plaintext
Encryption
ALRD HDS XGOOYYBW Ciphertext

16. The Substitution Cipher cont.

• To decrypt we just look up the ciphertext letter
in the table and then write down the matching
plaintext letter
• How many keys do we have now?
• A key is just a permutation of the letters of the
alphabet
• There are 26! permutations
• 403291461126605635584000000

17. Breaking the Substitution Cipher

• If we could do 1 000 000 calculations per second, it would take
over 12.7x1012 years to try all possible keys
• The universe is about 13.7x109 years old
• Trying all possible keys is probably not going to work

18. Frequency Analysis

• In English (or any language) certain letters are
used more often than others
• If we look at a ciphertext, certain ciphertext
letters are going to appear more often than
others
• It would be a good guess that the letters that
occur most often in the ciphertext are actually
the most common English letters

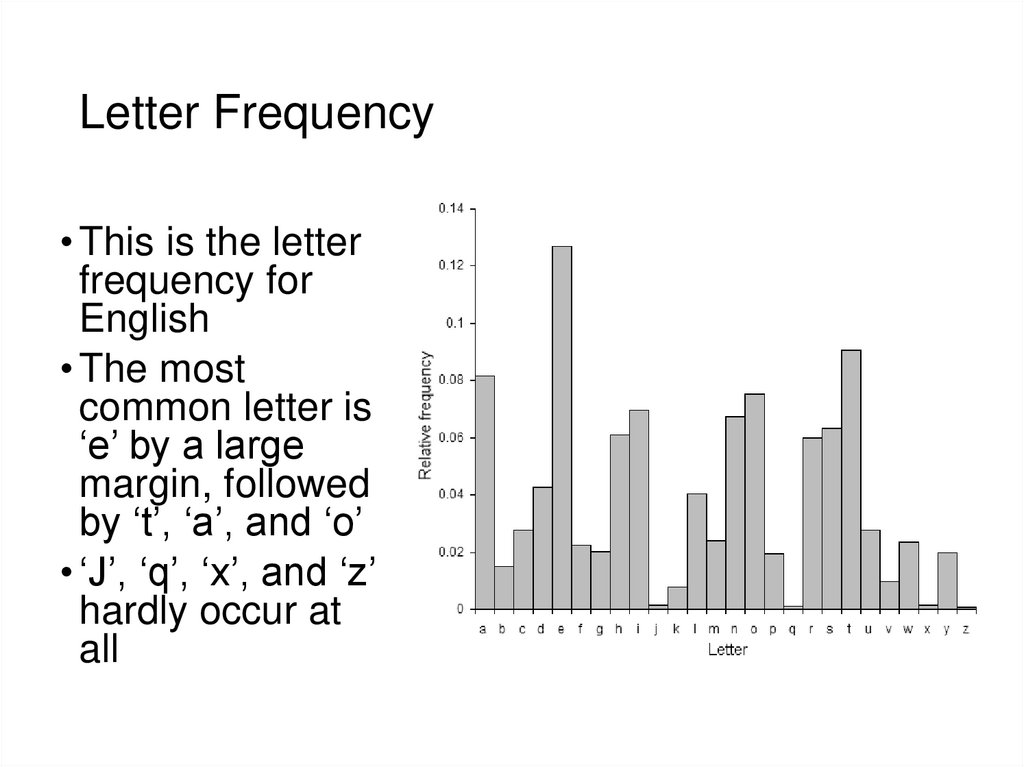
19. Letter Frequency

• This is the letter
frequency for
English
• The most
common letter is
‘e’ by a large
margin, followed
by ‘t’, ‘a’, and ‘o’
• ‘J’, ‘q’, ‘x’, and ‘z’
hardly occur at
all

20. Frequency Analysis in Practice

• Suppose this is our ciphertext
• dq lqwurgxfwlrq wr frpsxwlqj surylglqj d eurdg vxuyhb
ri wkh glvflsolqh dqg dq lqwurgxfwlrq wr surjudpplqj.
vxuyhb wrslfv zloo eh fkrvhq iurp: ruljlqv ri frpsxwhuv,
gdwd uhsuhvhqwdwlrq dqg vwrudjh, errohdq
dojheud, gljlwdo orjlf jdwhv, frpsxwhu dufklwhfwxuh,
dvvhpeohuv dqg frpslohuv, rshudwlqj vbvwhpv,
qhwzrunv dqg wkh lqwhuqhw, wkhrulhv ri
frpsxwdwlrq, dqg duwlilfldo lqwhooljhqfh.

21.

0.12
Relative Frequency
0.1
0.08
0.06
0.04
0.02
0
a b c d e f g h i j k l m n o p q r s t u v w x y z
Letter
Ciphertext distribution
English distribution
In our ciphertext we have one letter that occurs more often than any other (h), and
6 that occur a good deal more than any others (d, l, q, r, u, and w)
There is a good chance that h corresponds to e, and d, l, q, r, u, and w correspond
to the 6 next most common English letters

22. Frequency Analysis cont.

• If we replace ‘e’ with ‘h’ and the 6 next most
common letters with their matches, the
ciphertext becomes
• an intro???tion to ?o?p?tin? pro?i?in? a ?roa?
??r?e? o? t?e ?i??ip?ine an? an intro???tion to
pro?ra??in?. ??r?e? topi?? ?i?? ?e ??o?en ?ro?:
ori?in? o? ?o?p?ter?, ?ata repre?entation an?
?tora?e, ?oo?ean a??e?ra, ?i?ita? ?o?i? ?ate?,
?o?p?ter ar??ite?t?re, a??e???er? an? ?o?pi?er?,
operatin? ???te??, net?or?? an? t?e internet,
t?eorie? o? ?o?p?tation, an? arti?i?ia? inte??i?en?e.

23. Permutation cipher

A permutation cipher is a type of transposition cipher that
encrypts a message by rearranging the positions of its characters
according to a specific system or key, without altering the actual
characters themselves. This method ensures that the original
characters are present in the ciphertext, but their order is
shuffled, making the message unintelligible without the key.

24.

• Example:
• Let's encrypt the plaintext "HELLO WORLD" using the keyword
"GREAT":
• Step 1: Write the plaintext in rows under the keyword:
G R EAT
HELLO
WORLD
• Step 2: Label columns based on the alphabetical order of the
keyword:
AEGRT
LLHEO
LRWOD

25. The End