Overview. Beyond basic cryptography

1. Overview

Beyond basic cryptography:
o Secret splitting - divide a message into n pieces, such
that all n pieces must be combined to recover the
message
o Blind signatures – produce an unlinkable digital signature
o Bit commitment allows a user to commit to a prediction
without revealing it
o Cryptographic protocols make use of cryptography to
accomplish some task securely
Authentication
Key-exchange
o Zero-knowledge proofs allows a person to prove that he
knows a secret without revealing it
Chapter 6 Other Security Building Blocks
1

2. Motivation for Secret Splitting

A professor, Carol, encrypts her grade file
with a symmetric-key cryptosystem
o Good: only Carol can read grades (privacy)
o Good: only Carol can modify grades (integrity)
o Bad: if Carol becomes incapacitated nobody else
can recover the grades
Carol needs some kind of a mechanism that
will allow someone other than her to
decrypt the grade file in case of an
emergency
Chapter 6 Other Security Building Blocks
2

3. Secret Splitting

Secret splitting makes it possible to divide
a message into n pieces called shadows,
such that:
o Combining less than n shadows yields nothing
o Combining all n shadows yields the message
Carol can split her key into n shadows and
give one to n different people she trusts:
o Good: if Carol becomes incapacitated all n
people can get together and recover the grade
file
o Good: Unlikely that all n people would betray
Carol’s trust
Chapter 6 Other Security Building Blocks
3

4. Secret Splitting Using One-Time Pads

M = “THEKEYISTHREE”
Create four shadows:
Generate n-1 one-time pads (as long as M):
o P1 = PDJEUVNSKTUEG
o P2 = NBEXUYYKPAQJZ
o P3 = ICMKELDAOFGMC
Encrypt M with P1:
o C1 = JLOPZUYLEBMJL
T (20) + P (16) mod 26 = J (10)
H (8) + D (4) mod 26 = L (12)
E(5) + J (10) mod 26 = O (15)
…
Chapter 6 Other Security Building Blocks
4

5. Secret Split. with One-Time Pads

Encrypt C1 with P2:
o C2 = XNTNUTXWUCDTL
Encrypt C2 with P3:
o C3 = GQGYZFBXJIKGO
P1, P2, P3, and C3 are the four shadows
Good: all four shadows are required to reconstruct
M:
o Use P3 to decrypt C3 yielding C2
o Use P2 to decrypt C2 yielding C1
o Use P1 to decrypt C1 yielding M
Bad: What happens if Carol and one of the shadow
holders become incapacitated?
Chapter 6 Other Security Building Blocks
5

6. Secret Sharing

Secret sharing (also called a threshold scheme) makes it
possible to divide a message into n shadows, such that:
o Combining less than k shadows yields nothing
o Combining any k (or more) yields the message
Example:
o Carol uses a (3-8)-threshold scheme to divide her key into eight
shadows (any three required to recover M)
o Give three to Alice, one to Bob, two to Dave, and one each to Elvis
and Fred
o Carol’s key can be recovered by:
Alice (3)
Dave (2) and Bob (1)
Bob (1), Elvis (1), and Fred (1)
Etc.
Good: Need some, not all, shadows to recover the key
Chapter 6 Other Security Building Blocks
6

7. Motivation for Blind Sig’s

Dave owns a bank
Carol has an account at Dave’s bank
Carol wants to withdraw some digital money
Carol would like for the digital money to be:
o Valid – it should be accepted as payment by merchants
(perhaps after some verification procedure)
o Anonymous – Dave should not be able to determine where
Carol spends her money
Blind signatures allow Dave to create digital money
that is both valid and anonymous
Chapter 6 Other Security Building Blocks
7

8. Blind Signatures

Blind signatures enable a user to digitally sign a
document without seeing its contents
Assume Dave’s RSA public/private keys are:
o Public: e = 413, n = 629
o Private: d = 53
Before giving a message, m, to Dave for his
signature, Carol can blind it
o Choose a random blinding factor, b
1 < b < n-1
b is relatively prime to n
Example (using small numbers): m = 250 and b = 5
Chapter 6 Other Security Building Blocks
8

9. Blind Signatures (cont)

Carol blinds the message:
B = (m (be)) mod n
B = (250 (5413)) mod 629
B = 172
Carol gives the blinded message, B, to Dave
Dave cannot read the blinded message
because he does not know the blinding
factor
o If n is large, exhaustive search for b is
unfeasible
Chapter 6 Other Security Building Blocks
9

10. Blind Signatures (cont)

Dave
signs the blinded message as he
would any other message:
S’ = Bd mod n
S’ = 17253 mod 629
S’ = 168
Dave
sends the signed blinded
message, S’, to Carol
Chapter 6 Other Security Building Blocks
10

11. Blind Signatures (cont)

Carol unblinds the signed blinded message by
multiplying it by b’s multiplicative inverse modulo n
In our example, b = 5, so b-1 = 126 since
(126 5) mod 629 = 1
Carol computes:
S = (S’ b-1) mod n
S = (168 126) mod 629
S = 411
Note that the resulting digital signature, S = 411,
is identical to the one that would be produced by
Dave signing m = 250 with his private key!
Chapter 6 Other Security Building Blocks
11

12. Properties of Blind Signatures

Validity – as with normal digital signatures:
o Anyone can use Dave’s public key to verify his
signature on the document is valid
o Dave’s signature still cannot be forged or
moved to another document, and Dave cannot
repudiate his signature
Unlinkability – unlike normal digital
signatures:
o Dave cannot subsequently link the unblinded
signed document to the blind document that he
signed
Chapter 6 Other Security Building Blocks
12

13. Unlinkability of Blind Signatures

Suppose:
o Carol gives Dave two blinded documents to sign
o Dave signs them, returns them to Carol, and
keeps copies of the two blind documents
o Carol unblinds them and gives Dave copies of
the two unblinded documents bearing his
signature
Then:
o Dave will not be able to determine which
unblinded document corresponds to which
blinded document
Chapter 6 Other Security Building Blocks
13

14. Example of Unlinkability

Carol gives Dave two blinded documents to sign
o B1 = 542, B2 = 492
Dave signs them, returns them to Carol, and keeps copies of
the two blind documents
Carol unblinds them and gives Dave copies of the two
unblinded documents bearing his signature
o S1 = 217, S2 = 121
Dave can verify his signature and learn the contents of the
documents he signed:
o m1 = 217413 mod 629 = 200, m2 = 121413 mod 629 = 100
Dave cannot link an unblinded document to the corresponding
blind document:
o B1 = m1 and B2 = m2?
o B1 = m2 and B2 = m1?
Chapter 6 Other Security Building Blocks
14

15. Example of Unlinkability (cont)

To link an unblinded document to the corresponding blind
document
o B1 (542) = m1 (200) and B2 (492) = m2 (100), or
o B1 (542) = m2 (100) and B2 (492) = m1 (200)
Dave must determine the blinding factor used to blind each
document
Dave can use exhaustive search to find the blinding factors:
o b1 = 409 since (100 × 409413) mod 629 = 542
o b2 = 557 since (200 × 557413) mod 629 = 492
Dave knows that the first blind document he signed, B1, was
m2 and the second blind document was m1
For large values of n, exhaustive search is not feasible and
therefore the signatures are unlinkable
Chapter 6 Other Security Building Blocks
15

16. Motivation for Blind Signatures (cont)

Why would Dave sign a blind document that he
could not read and create an unlinkable signature?
Recall:
o Dave owns a bank
o Carol has an account at Dave’s bank
o Carol wants to withdraw some digital money
o Carol would like for the digital money to be:
Valid – it should be accepted as payment by merchants
(perhaps after some verification procedure)
Anonymous – Dave should not be able to determine where
Carol spends her money
o Blind signatures allow Dave to create digital money that
is both valid and anonymous
Chapter 6 Other Security Building Blocks
16

17. Digital Money Without Blind Sig’s

Carol creates a message containing a serial number and a
value
o Serial number = 603482, Value = $10
Dave signs the message and deducts $10 from Carol’s
account
Carol uses the signed message to pay a merchant
o The merchant uses Dave’s public key to verify his signature
The merchant redeems the money with Dave for $10
Good: Carol’s digital money is valid
Bad: Carol’s digital money is not anonymous
o Dave could keep a record each serial number and to whom it was
issued
o When a merchant redeems digital money Dave could determine
to whom that money was issued
Chapter 6 Other Security Building Blocks
17

18. Digital Money With Blind Signatures

Carol creates a message containing a serial number and a
value
o Serial number = 603482, Value = $10
Carol blinds the message before giving it to Dave to sign
Dave does not know the blinding factor so he cannot see the
contents of the message (e.g. the serial number)
Dave signs the message and deducts $10 from Carol’s
account
Carol unblinds the message uses the signed message to pay a
merchant
o The merchant uses Dave’s public key to verify his signature
The merchant redeems the money with Dave for $10
Good: Carol’s digital money is valid
Good: Carol’s digital money is anonymous
Chapter 6 Other Security Building Blocks
18

19. Digital Money With Blind Signatures (cont)

Problem #1: double spending
o Carol uses her digital money to pay one merchant
The merchant uses Dave’s public key to verify it is valid
o Carol uses the same piece of digital money to pay another
merchant
The merchant uses Dave’s public key to verify it is valid
o Twenty dollars worth of digital money has cost Carol $10
Solution: merchant must check with Dave and
make sure the digital money has not already been
spent before accepting it
Chapter 6 Other Security Building Blocks
19

20. Digital Money With Blind Signatures (cont)

Problem #2: fraud
o Carol creates a message worth $1000
o Carol blinds the message before giving it to Dave to sign
telling him it is worth $10
Dave does not know the blinding factor so he cannot see the
contents of the message
o Dave signs the message and deducts $10 from Carol’s
account
o $1,000 worth of digital money has cost Carol $10
Solution: Dave needs to be pretty sure of the
value of the digital money without actually seeing
it (and the serial number)
Chapter 6 Other Security Building Blocks
20

21. Digital Money With Blind Signatures (cont)

Dave requires Carol to create and submit 100
messages:
m1 = “Serial number = 935076, Value = $10”
m2 = “Serial number = 104766, Value = $10”
...
m100 = “Serial number = 337147, Value = $10”
Carol chooses 100 different blinding factors, b1,
b2, …, b100
Carol uses the blinding factors to create 100
blinded messages
Carol gives all 100 blinded messages to Dave and
tells him their value ($10 each in this case)
Chapter 6 Other Security Building Blocks
21

22. Digital Money With Blind Signatures (cont)

Dave chooses 99 of the 100 messages at random
to challenge
Dave asks Carol for the corresponding blinding
factors
Dave unblinds each of the 99 messages and checks
to see that each is worth $10
If all checks succeed Dave signs the one blind
message he did not challenge and returns it to
Carol
Carol unblinds the message
Carol now has a valid, anonymous piece of digital
money from Dave
Chapter 6 Other Security Building Blocks
22

23. Digital Money With Blind Signatures (cont)

For Carol to get $1,000 worth of digital
money for $10 she would have to:
o Create 99 messages containing the value $10
o Create one message containing the value $1,000
o Hope that the $1,000 message is the one
message that Dave does not challenge
Carol’s chances of succeeding are one in
100
Dave can lower the odds of fraud by
requiring 1,000 or 1,000,000 messages to
be submitted
Chapter 6 Other Security Building Blocks
23

24. Motivation for Bit Commitment

Might want to commit to a prediction without revealing it
Chuck and Bill’s virtual coin flips – Scenario #1
o
o
o
o
Chuck thinks of a value, either ‘heads’ or ‘tails’
Bill announces his guess
Chuck tells Bill his value
Problem: Chuck can cheat Bill
Chuck has not committed to a value - he can change it after Bill
guesses
Chuck and Bill’s virtual coin flips – Scenario #2
o
o
o
o
Bill thinks of his guess
Chuck thinks of a value and announces it to Bill
Bill tells Chuck his guess
Problem: Bill can cheat Chuck
Chuck had to reveal his value in order to commit to it
Chapter 6 Other Security Building Blocks
24

25. Motivation for Bit Commitment (cont)

Chuck and Bill’s virtual coin flips – Scenario #3
o Chuck chooses a value, writes it on a piece of paper, seals
it in an envelope, and hands the envelope to Bill
o Bill announces his guess
o Bill opens the envelope and both learn whether Bill was
right
o Good: neither can cheat
Fairness requirements:
o Chuck must commit to his value in such a way that:
Chuck cannot subsequently change the value
Bill does not learn Chuck’s value until after Bill has guessed
Chapter 6 Other Security Building Blocks
25

26. Bit Commitment

Bit commitment allows someone to commit to a
prediction without revealing it
Bit commitment has two phases:
o Commitment phase: one party commits to a prediction in
such a way that it cannot be subsequently changed
o Verification phase: the second party learns the first
party’s prediction
Cheating is impossible if:
o The prediction cannot be changed after the commitment
phase
o The prediction is not revealed until the verification
phase
Chapter 6 Other Security Building Blocks
26

27. Bit Commitment Using a Symmetric-Key Cryptosystem

Commitment phase:
o Chuck chooses a random key, k, and encrypts his
prediction
M = Encrypt(p,k)
o Chuck gives a copy of M to Bill
Problem: easy for Chuck to change prediction by
finding M such that:
o Decrypt(M, k1) = 0, and
o Decrypt(M, k2) = 1
Solution:
o Bill send a random string of bits, R, to Chuck
o Chuck concatenates his prediction to R and then
encrypts:
M = Encrypt(“Rp”, k)
Chapter 6 Other Security Building Blocks
27

28. Bit Commitment Using a Symmetric-Key Cryptosystem

Commitment phase:
o Bill send a random string of bits, R, to Chuck
o Chuck concatenates his prediction to R and then
encrypts:
M = Encrypt(“Rp”, k)
o Chuck gives a copy of M to Bill
Verification phase:
o Chuck sends k to Bill
o Bill decrypts M, checks R, and learns p:
Decrypt (M, k)
Chapter 6 Other Security Building Blocks
28

29. Bit Commitment Using a Symmetric-Key Cryptosystem

Neither can cheat:
o The prediction cannot be changed after the
commitment phase
A good cryptosystem will not allow Chuck to create an
M such that:
Decrypt(Rp1,k1) = M
Decrypt(Rp2,k2) = M
o The prediction is not revealed until the
verification phase
Bill does not know the key Chuck chose and connot
read M without it
Chapter 6 Other Security Building Blocks
29

30. Bit Commitment Using a One-Way Hash Function

Commitment phase:
o Chuck creates two random strings of bits, R1 and R2
o Chuck concatenates R1, R2, and his prediction, p, and
sends the result through the one-way hash function, H:
h = H(R1R2p)
o Chuck sends h and R1 to Bill
Verification phase:
o Chuck sends R2 and p to Bill
o Bill computes the hash:
h’ = H(R1R2p)
o Bill verifies that h’ = h
Chapter 6 Other Security Building Blocks
30

31. Bit Commitment Using a One-Way Hash Function

Neither can cheat:
o The prediction cannot be changed after the
commitment phase
A good one-way hash function will not allow Chuck to
create an R1, R2, and p such that there is a collision:
H(R1R2p1) = h
H(R1R3p2) = h
o The prediction is not revealed until the
verification phase
Since the hash function is one-way, Bill cannot deduce
p from h and R1
Chapter 6 Other Security Building Blocks
31

32. Cryptographic Protocols

A protocol is an agreed-upon sequence of
actions performed by two or more
principals
Cryptographic protocols make use of
cryptography to accomplish some task
securely
Example:
o How can Alice and Bob agree on a session key to
protect a conversation?
o Answer: use a key-exchange cryptographic
protocol
Chapter 6 Other Security Building Blocks
32

33. Key Exchange with Symmetric Cryptography

Assume Alice and Bob each share a key
with a Key Distribution Center (KDC)
o KA is the key shared by Alice and the KDC
o KB is the key shared by Bob and the KDC
To agree on a session key:
o Alice contacts the KDC and requests a session
key for Bob and her
o The KDC generates a random session key,
encrypts it with both KA and KB, and sends the
results to Alice
Chapter 6 Other Security Building Blocks
33

34. Key Exchange with Symmetric Cryptography (cont)

Agreeing on a session key (cont):
o Alice decrypts the part of the message
encrypted with KA and learns the session key
o Alice sends the part of the message encrypted
with KB to Bob
o Bob receives Alice’s message, decrypts it, and
learns the session key
o Alice and Bob communicate securely using the
session key
Chapter 6 Other Security Building Blocks
34

35. Key Exchange with Symmetric Cryptography (cont)

The
key-exchange protocol:
A: => KDC (A,B);
KDC: => A (E(KAB,KA), E(KAB,KB));
A: => B (E(KAB,KB));
Chapter 6 Other Security Building Blocks
35

36. Key Exchange with Symmetric Cryptography (cont)

Issues:
o Security depends on secrecy of KA and KB
KDC must be secure and trusted by both Alice and
Bob
KA and KB should be used sparingly
o The use of a new session key for each
conversation limits the chances/value of
compromising a session key
Chapter 6 Other Security Building Blocks
36

37. Attacking the Protocol

Alice and Bob set up a secure session protected by KAB
An intruder, Mallory, watches them do this and stores the
KDC’s message to Alice and all the subsequent messages
between Alice Bob encrypted with KAB
Mallory cryptanalyzes the session between Alice and Bob and
eventually recovers KAB
The next time Alice and Bob want to talk Mallory intercepts
the KDC’s reply and replays the old message containing KAB
Alice and Bob conduct a “secure” conversation which is
protected by KAB which is known to Mallory
Chapter 6 Other Security Building Blocks
37

38. Attacking the Protocol (cont)

A: => KDC (A,B);
KDC: => A (E(KAB,KA), E(KAB,KB));
A: => B (E(KAB,KB));
// Alice and Bob encrypt their messages using KAB
// Mallory recovers KAB by analyzing Alice and Bob’s session
A: => KDC (A,B);
KDC: => A (E(KAB’,KA), E(KAB’,KB));
// Mallory intercepts the above message and replaces it
M: => A (E(KAB,KA), E(KAB,KB));
A: => B (E(KAB,KB));
// Mallory reads all traffic session between Alice and Bob
Chapter 6 Other Security Building Blocks
38

39. What Went Wrong?

Alice and Bob need to be able to
distinguish between a current (or fresh)
response from the KDC and an old one
Solutions:
o Alice and Bob could keep track of all previously-
used session keys and never accept an old
session key
o KDC could include freshness information in its
messages
Timestamps
Nonces
Chapter 6 Other Security Building Blocks
39

40. Using Timestamps to Establish Freshness

A: => KDC (A,B);
KDC: => A (E((KAB,TKDC),KA), E((KAB,TKDC),KB));
A: => B (E((KAB,TKDC),KB));
Where TKDC is a timestamp from the KDC’s
clock and:
Alice and Bob’s clocks are both synchronized with
the KDC’s
Alice and Bob both check the KDC’s message to
make sure it was generated recently
Chapter 6 Other Security Building Blocks
40

41. Using Nonces to Establish Freshness

A nonce is a randomly-generated value
that:
o Is never reused
o Can be used to prove the freshness of a
message
A: => KDC (A,B,NA);
B: => KDC (A,B, NB);
KDC: => A (E((KAB,NA),KA));
KDC: => B (E((KAB,NB),KB));
Chapter 6 Other Security Building Blocks
41

42. Key-Exchange with Public-Key Cryptography

Alice learns Bob’s public key (by either
asking Bob or some third party)
Alice generates a random session key, KAB
Alice encrypts the session key with Bob’s
public key
Alice sends Encrypt(KAB,BPublic) to Bob
Bob receives Alice’s message and decrypts
it with his private key
Alice and Bob encrypt their subsequent
communications with KAB
Chapter 6 Other Security Building Blocks
42

43. Attacking the Protocol

Recall the man-in-the-middle attack
o If Mallory can trick Alice into thinking that
MPublic is Bob’s public key
Mallory can decrypt Alice’s first message to Bob
Encrypt(KAB,MPublic)
Mallory learns the proposed session key KAB
Mallory can send Bob: Encrypt(KAB,BPublic)
Alice and Bob will encrypt their subsequent
communications with KAB thinking that it is secure
This is a very serious problem because it’s
often difficult to be sure you know
somebody’s public key
Chapter 6 Other Security Building Blocks
43

44. The Interlock Protocol

Combating the man-in-the-middle attack:
o Alice and Bob exchange public keys
o Alice encrypts her message using Bob’s public key. Alice
sends half the encrypted message to Bob (e.g. every
other bit)
o Bob encrypts his message using Alice’s public key. Bob
sends half the encrypted message to Alice (e.g. every
other bit)
o Alice sends the other half of her encrypted message to
Bob. Bob puts the two halves together and decrypts them
using his private key
o Bob sends the other half of his encrypted message to
Alice. Alice puts the two halves together and decrypts
them using her private key
Chapter 6 Other Security Building Blocks
44

45. The Interlock Prot. (cont)

Foiling the man-in-the-middle:
o Assume Mallory can trick Alice into using MPublic instead
o
o
o
o
o
of BPublic
When Mallory receives the first half of Alice’s message
she won’t be able to decrypt it and re-encrypt it with
BPublic
Mallory must invent a completely new message, encrypt it
and send half of it to Bob
When the second half of Alice’s message arrives, Mallory
can put the two halves together, decrypt, and learn what
Alice’s original message was
However, Mallory has already committed to the first half
of the message and it is too late to change
Therefore, Bob will not get the message Alice sent, and
Alice and Bob will probably be able to figure out that
there is an intruder between them
Chapter 6 Other Security Building Blocks
45

46. Authentication

Authentication is the process of proving
your identity to someone else
o One-way
o Two-way
Authentication protocols are often
designed using a challenge and response
mechanism
o Authenticator creates a random challenge
o Authenticatee proves identity by replying with
the appropriate response
Chapter 6 Other Security Building Blocks
46

47. One-way Authentication Using Symmetric-Key Cryptography

Assume that Alice and Bob share a secret
symmetric key, KAB
One-way authentication protocol:
o Alice creates a nonce, NA, and sends it to Bob as a
challenge
o Bob encrypts Alice’s nonce with their secret key and
returns the result, Encrypt(NA, KAB), to Alice
o Alice can decrypt Bob’s response and verify that the
result is her nonce
A: => B(NA);
B: => A(Encrypt(NA, KAB));
Chapter 6 Other Security Building Blocks
47

48. One-way Authentication Using Symmetric-Key Cryptography

Problem: an adversary, Mallory, might be able to
impersonate Bob to Alice:
o Alice sends challenge to Bob (intercepted by Mallory)
o Mallory does not know KAB and thus cannot create the
appropriate response
o Mallory may be able to trick Bob (or Alice) into creating
the appropriate response for her:
A: => M(NA);
M: => B(NN);
B: => M(Encrypt(NA, KAB));
M: => A(Encrypt(NA, KAB));
Chapter 6 Other Security Building Blocks
48

49. One-way Authentication Using Public-Key Cryptography

Alice sends a nonce to Bob as a challenge
Bob replies by encrypting the nonce with his
private key
Alice decrypts the response using Bob’s public key
and verify that the result is her nonce
A: => B(NA);
B: => A(Encrypt(NA, BPrivate));
Encrypting any message that someone sends as an
authentication challenge might not be a good idea
Chapter 6 Other Security Building Blocks
49

50. One-way Authentication Using Public-Key Cryptography

Another challenge-and-response authentication
protocol:
o Alice performs a computation based on some random
numbers (chosen by Alice) and her private key and sends
the result to Bob
o Bob sends Alice a random number (chosen by Bob)
o Alice makes some computation based on her private key,
her random numbers, and the random number received
from Bob and sends the result to Bob
o Bob performs some computations on the various numbers
and Alice’s public key to verify that Alice knows her
private key
Advantage: Alice never encrypts a message chosen
by someone else
Chapter 6 Other Security Building Blocks
50

51. Authentication and Key-Exchange Protocols

Combine authentication and key-exchange
Assume Carla and Diane are on opposite ends of a
network and want to talk securely
o Want to agree on a new session key securely
o Want to each be sure that they are talking to the other
and not an intruder
Wide-Mouth Frog
o Assumes a trusted third-party, Sam, who shares a secret
keys, KC and KD, respectively, with Carla and Diane
Chapter 6 Other Security Building Blocks
51

52. Authentication and Key-Exchange Protocols

Wide-Mouth Frog
C: => S(C,Encrypt((D,KCD,TC),KCS));
S: => D(Encrypt((C, KCD, TS), KDS));
Observations:
o Reliance on synchronized clocks to generate
timestamps
o Depends on a third-party that both participants
trust
o Initiator is trusted to generate good session keys
Chapter 6 Other Security Building Blocks
52

53. Authentication and Key-Exchange Protocols

Yahalom
C => D (C,NC);
D => S (D,Encrypt((C,NC,ND),KD));
S => C (Encrypt((D,KCD,NC,ND),KC),Encrypt((C,KCD),KD));
C => D (Encrypt((C,KCD),KD),Encrypt(ND,KCD));
Note: Diane is the first one to contact Sam
who only sends one message to Carla
Chapter 6 Other Security Building Blocks
53

54. Authentication and Key-Exchange Protocols

Denning and Sacco (public-key)
o Carla sends a message to Sam including her name and Diane’s
name
o Sam replies with signed copies of both Carla and Diane’s
public key
C: => S(C,D);
S: =>
C(Encrypt((C,CPublic,TS),SPriavte),Encrypt((D,DPublic,TS),SPriavte));
C: =>
D(Encrypt((C,CPublic,TS),SPriavte),Encrypt((D,DPublic,TS),SPriavte));
o Carla generates the session key, KCD, and signed a message
containing it and a timestamp with her private key
C: => D(Encrypt(Encrypt((KCD,TC),CPrivate),DPublic));
Chapter 6 Other Security Building Blocks
54

55. Authentication and Key-Exchange Protocols

A weakness of the Denning and Sacco protocol
o Harry can trick Diane into thinking that she is
communicating with Carla when she is really
communicating with Harry
o Harry establishes a session key, KCH, with Carla
C: => H(Encrypt(Encrypt((KCH,TC),CPrivate),HPublic));
o Harry decrypts Carla’s message and learns KCH
o Harry encrypts Carla’s signed message with Diane’s public
key, and sends the result to Diane claiming to be Carla
H: => D(Encrypt(Encrypt((KCH,TC),CPrivate),DPublic));
o Diane will decrypt the message, check the signature and
timestamp, and believe that she is talking to Carla with
KCH as the session key
Chapter 6 Other Security Building Blocks
55

56. Authentication and Key-Exchange Protocols

Fixing
the Denning and Sacco
protocol:
o Add the other party’s name to the key
exchange message:
C: =>
D(Encrypt(Encrypt((D,KCD,TC),CPrivate),DPublic));
Chapter 6 Other Security Building Blocks
56

57. Motivation for Zero Knowledge Proofs

Many challenge and response authentication
protocols
o Prove identity by demonstrating knowledge of a certain
piece of information (e.g. a password)
o Bob authenticates Alice based on her knowledge of a
secret, S
Only Alice knows the secret, S
This person knows
Therefore, this person is Alice
Drawbacks:
o Requires Alice to disclose S to Bob
Bob may subsequently be able to impersonate Alice
Chapter 6 Other Security Building Blocks
57

58. Zero-Knowledge Proofs

Alice can perform a zero-knowledge proof so that:
o Bob can verify that Alice knows the secret
o Bob does not gain any information about the secret
Overview:
o Bob will ask Alice a series of questions
o For each question:
If Alice knows the secret she will have a 100% chance of answering
correctly
If Alice does not know the secret she will have a 50% chance of
answering correctly
o If Alice answers many questions in row correctly chances are
good that she knows the secret
o None of the questions or answers give Bob any information
about Alice’s secret
Chapter 6 Other Security Building Blocks
58

59. Zero-Knowledge Proofs (cont)

Bob asks Alice up to n questions
o If Alice ever answers incorrectly, Bob stops and knows Alice
does not know S
o If Alice always answers correctly, she probably knows S
How many questions should Bob ask?
o n=1
Efficient but chance of getting fooled
Alice’s odds of guessing right once are 1 in 2
o n = 10
Less efficient, less chance of getting fooled
Alice’s odds of guessing right ten times are 1 in 210 (~1,000)
o n = 20
Much less efficient, little chance of getting fooled
Alice’s odds of guessing right twenty times are 1 in 220 (~1,000,000)
Chapter 6 Other Security Building Blocks
59

60. The Zero-Knowledge Cave

A cave with a single entrance
The entry passage forks into left and right
passages
The two passages eventually meet each
other
A door has been built where they join
o The only way to open the door is to say the
“magic words”
Chapter 6 Other Security Building Blocks
60

61. The Zero-Knowledge Cave (cont)

Chapter 6 Other Security Building Blocks
61

62. The Zero-Knowledge Cave (cont)

Alice can prove to Bob that she knows the magic
words
Alice need not reveal the magic words to Bob:
o Alice and Bob stand at the entrance to the cave
o Alice walks all the way into the cave until she is standing
at the door
o Bob walks into the cave and to the fork
Bob does not know whether Alice chose to take the left or
the right passage to the door
o Bob chooses at random to ask Alice to come out of either
the passage to Bob’s right or the one to his left
o Alice exits from the appropriate passage (using the
magic words if necessary)
Chapter 6 Other Security Building Blocks
62

63. The Zero-Knowledge Cave

There are four possiblities:
(1) Alice enters the left passage and Bob asks her to come out the
left
Alice does not need to pass through the door
(2) Alice enters the left passage and Bob asks her to come out the
right
Alice must say the magic words to pass through the door
(3) Alice enters the right passage and Bob asks her to come out the
left
Alice must say the magic words to pass through the door
(4) Alice enters the right passage and Bob asks her to come out the
right
Alice does not need to pass through the door
If Alice knows the magic words she can come out of the
proper passage 100% of the time
If Alice does not know the magic words she can come out of
the proper passage 50% of the time
Chapter 6 Other Security Building Blocks
63

64. The Zero-Knowledge Cave (cont)

No matter how many times this protocol is run Bob
learns nothing about Alice’s secret
If Alice is able to complete 20 successful exits
from the cave then either:
(1) Bob’s requests were not random (Alice was able to
predict them)
(2) There was no barrier in the cave
(3) Alice guessed correctly 20 times in a row (~1 in
1,000,000)
(4) Alice knew the secret
So when performing a zero-knowledge proof, Bob
should try to make sure neither (1) nor (2) hold
Chapter 6 Other Security Building Blocks
64

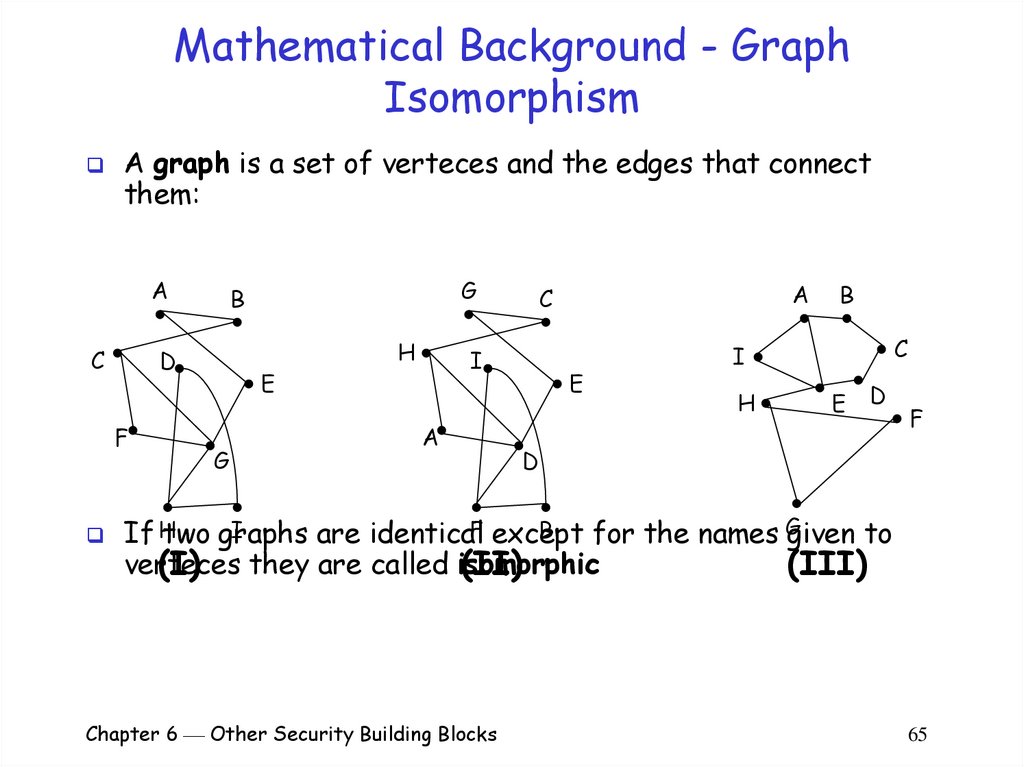
65. Mathematical Background - Graph Isomorphism

A graph is a set of verteces and the edges that connect
them:
A
C
D
F
G
B
E
G
H
I
A
A
C
E
B
C
I
H
E
D
F
D
I
B
If Htwo graphs
are identicalF except
for the names Ggiven to
verteces
(I) they are called isomorphic
(II)
(III)
Chapter 6 Other Security Building Blocks
65

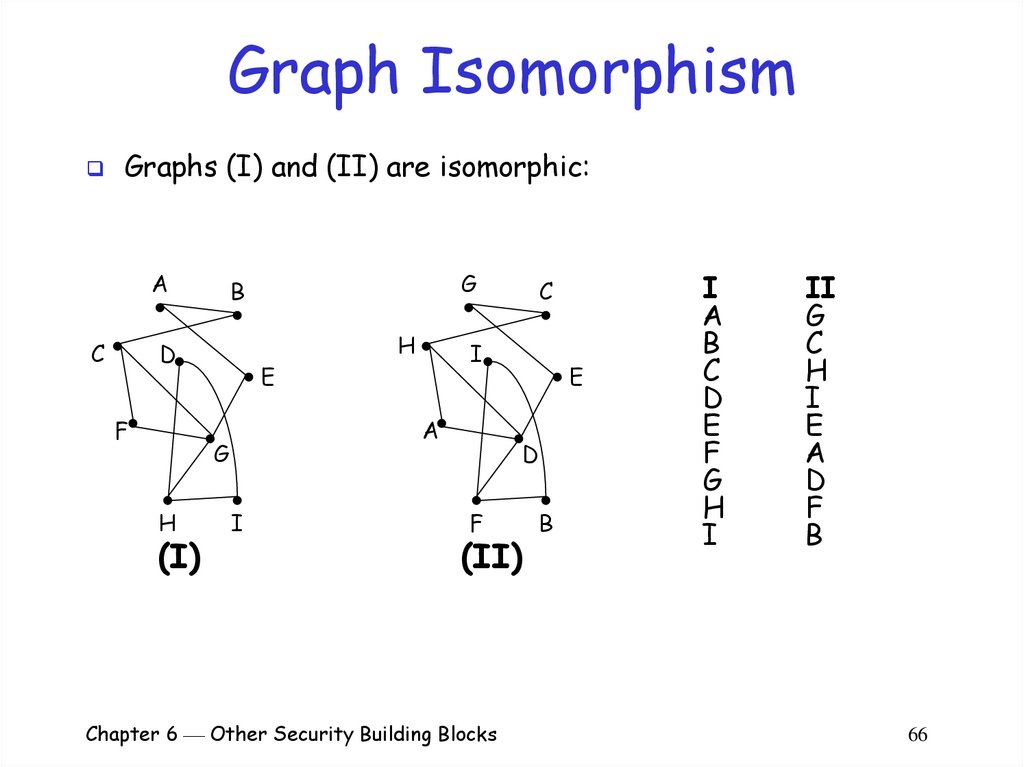
66. Graph Isomorphism

Graphs (I) and (II) are isomorphic:
A
C
D
F
E
(I)
H
I
C
I
A
G
H
G
B
E
D
F
(II)
Chapter 6 Other Security Building Blocks
B
I
A
B
C
D
E
F
G
H
I
II
G
C
H
I
E
A
D
F
B
66

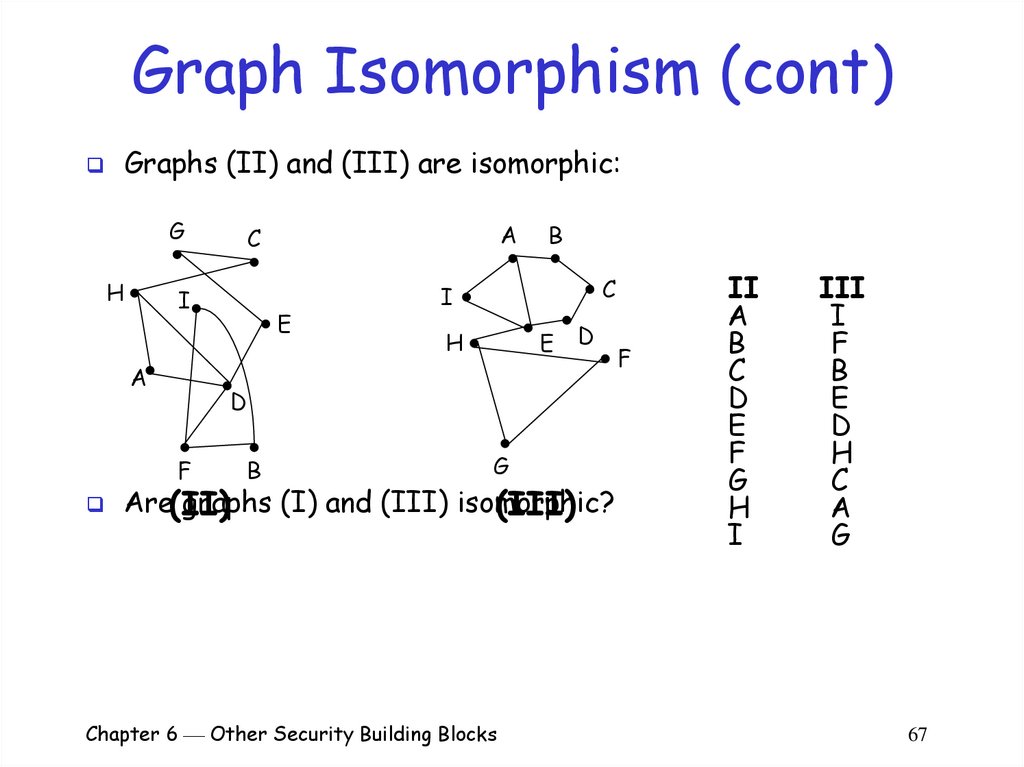
67. Graph Isomorphism (cont)

Graphs (II) and (III) are isomorphic:
G
H
I
A
E
B
C
I
H
E
D
D
F
A
C
B
G
Are(II)
graphs (I) and (III) isomorphic?
(III)
Chapter 6 Other Security Building Blocks
F
II
A
B
C
D
E
F
G
H
I
III
I
F
B
E
D
H
C
A
G
67

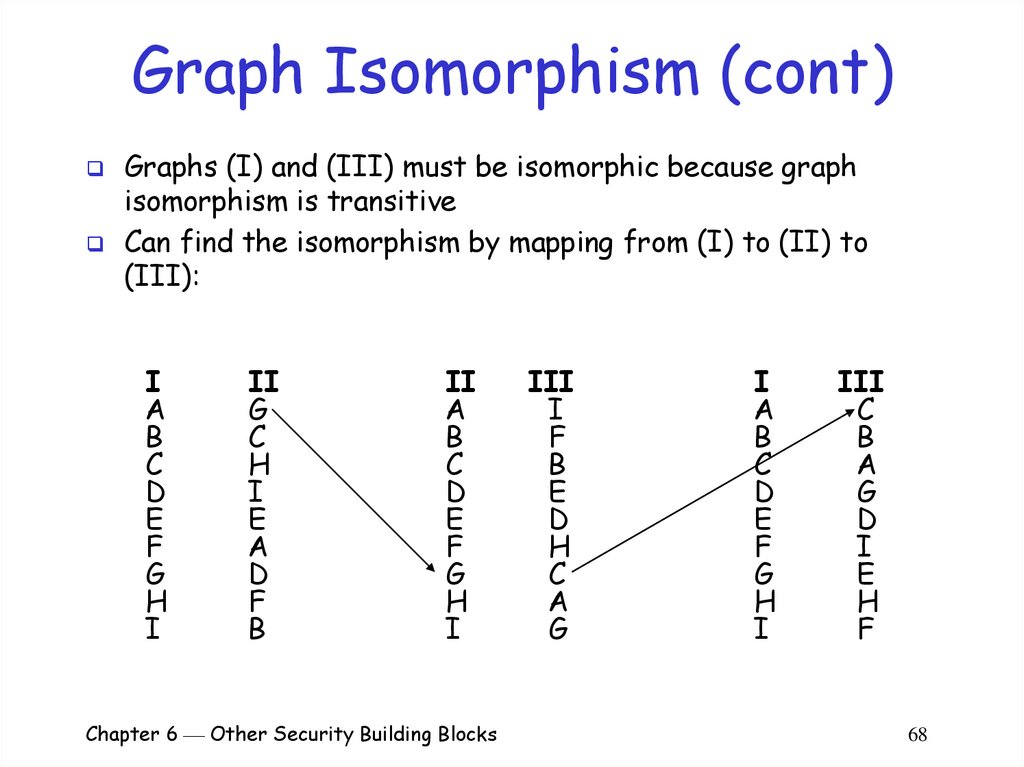
68. Graph Isomorphism (cont)

Graphs (I) and (III) must be isomorphic because graph
isomorphism is transitive
Can find the isomorphism by mapping from (I) to (II) to
(III):
I
A
B
C
D
E
F
G
H
I
II
G
C
H
I
E
A
D
F
B
II
A
B
C
D
E
F
G
H
I
Chapter 6 Other Security Building Blocks
III
I
F
B
E
D
H
C
A
G
I
A
B
C
D
E
F
G
H
I
III
C
B
A
G
D
I
E
H
F
68

69. Graph Isomorphism is a Hard Problem

In general, determining whether two
graphs are isomorphic is a difficult
problem:
o Best-known algorithm runs in time exponential
to the number of verteces
As the number of verteces gets large, finding an
answer is intractable
o A claimed isomorphism between two graphs can
be checked in polynomial time
As the number of verteces gets large, verifying an
answer is tractable
Chapter 6 Other Security Building Blocks
69

70. A Zero-Knowledge Proof Using Graph Isomorphism

Alice creates two graphs, G1 and G2, which
are isomorphic to each other:
o Randomly create G1
o Randomly permute the verteces of G1 to create
G2
o Save the permutation of G1’s verteces used to
produce G2
It is the isomorphism between the two
Alice can use a zero-knowledge proof to
convince Bob that she knows the
isomorphism without revealing it
Chapter 6 Other Security Building Blocks
70

71. Zero-Knowledge Proof Using Graph Isomorphism

Alice randomly permutes G1 to produce another
graph, H, which is isomorphic to both G1 and G2
o Alice knows the isomorphism between G1 and G2
o Alice knows the isomorphism between G1 and H
o Alice knows the isomorphism between G2 and H (by
transativity)
o For anybody who does not know the isomorphism between
G1 and G2:
Finding the isomorphism between G1 and G2 is “hard”
Finding the isomorphism between G1 and H is as hard as
finding the isomorphism between G1 and G2
Finding the isomorphism between G2 and H is as hard as
finding the isomorphism between G1 and G2
Chapter 6 Other Security Building Blocks
71

72. Zero-Knowledge Proof Using Graph Isomorphism

Alice and Bob repeat the following protocol until
Bob is satisfied:
o Alice randomly permutes G1 to produce another graph, H
o Alice sends H to Bob
o Bob asks Alice either to:
Prove that H and G1 are isomorphic, or
Prove that H and G2 are isomorphic
o Alice complies (without providing the other isomorphism)
o Bob verifies whether or not Alice’s answer is correct
Chapter 6 Other Security Building Blocks
72

73. Zero-Knowledge Proof Using Graph Isomorphism

Without knowing the isomorphism between G1 and
G2 Alice cannot create a graph H for which she
knows the isomorphism to both G1 and G2
o Otherwise she would know the isomorphism between G1
and G2 by transitivity
In each round Alice’s must choose:
o Permute G1 to produce a graph, H1, for which she knows
the isomorphism to G1 (but not G2), or
o Permute G2 to produce a graph, H2, for which she knows
the isomorphism to G2 (but not G1)
Chapter 6 Other Security Building Blocks
73

74. Zero-Knowledge Proof Using Graph Isomorphism

Alice only sends one graph to Bob in each round
Four possibilities each round:
o Alice sends
answer
o Alice sends
answer
o Alice sends
answer
o Alice sends
answer
H1 and Bob asks for (H1,G1): Alice will be able to
H1 and Bob asks for (H1,G2): Alice will not be able to
H2 and Bob asks for (H2,G1): Alice will not be able to
H2 and Bob asks for (H2,G2): Alice will be able to
Results:
o Alice has a 50% chance in each round of answering correctly
whether or not she knows the isomorphism between G1 and G2
o Each round Bob learns the isomorphism between a random graph
and either G1 or G2
Chapter 6 Other Security Building Blocks
74

75. Zero-Knowledge Proof Using Graph Isomorphism

If Alice is able to answer correctly 20
times in a row:
(1) Bob’s requests were not random
–
Alice was able to predict them and generate H
accordingly
(2) Graph isomorphism is not a hard problem
(3) Alice guessed correctly 20 times in a row
(4) Alice knew the secret
Chapter 6 Other Security Building Blocks
75

76. Problem With Zero-Knowledge Proofs

Remember the man-in-the-middle attack?
Carol is going to prove to Bob that she knows the isomorphism
between G1 and G2 (even though she doesn’t)
o Carol asks Alice to prove she knows the isomorphism
o Alice generates a graph, H, and sends it to Carol
o Carol contacts Bob and says she’s ready to start the proof; she sends H
to Bob
o Bob chooses either G1 or G2 and asks Carol for the isomorphism
o Carol asks Alice the same question
o Alice answers Carol
o Carol repeats the answer to Bob
Results:
o Carol will answer Bob correctly in every round
o Bob will believe that Carol knows the isomorphism
o Carol does not know the isomorphism
Chapter 6 Other Security Building Blocks
76

77. Summary

Beyond basic cryptography:
o Secret splitting - divide a message into n pieces, such
that all n pieces must be combined to recover the
message
o Blind signatures – produce an unlinkable digital signature
o Bit commitment allows a user to commit to a prediction
without revealing it
o Cryptographic protocols make use of cryptography to
accomplish some task securely
Authentication
Key-exchange
o Zero-knowledge proofs allows a person to prove that he
knows a secret without revealing it
Chapter 6 Other Security Building Blocks
77