Формула полной вероятности. Формула Байеса

1.

ФОРМУЛА ПОЛНОЙ
ВЕРОЯТНОСТИ. ФОРМУЛА БАЙЕСА
Практическая работа

2.

Формула полной вероятности
Если событие А не может произойти
само по себе, а лишь после того как
произойдет одно из событий
Н1, Н2 , ... Нn
составляющих полную группу
n
несовместных событий,
P H i 1
i 1

3.

Формула полной вероятности
тогда вероятность события А находится
по формуле полной вероятности
n
Р А Р Н i Р А / Н i
i 1

4.

Формула Байеса
Если событие А (из задачи на формулу полной
вероятности) уже произошло,
то можно переоценить первоначальную
вероятность гипотез по формуле Байеса
Р( Н k ) Р( A / H k )
Р( Н k / А ) n
Р( Н i ) Р( А / Н i )
i 1

5.

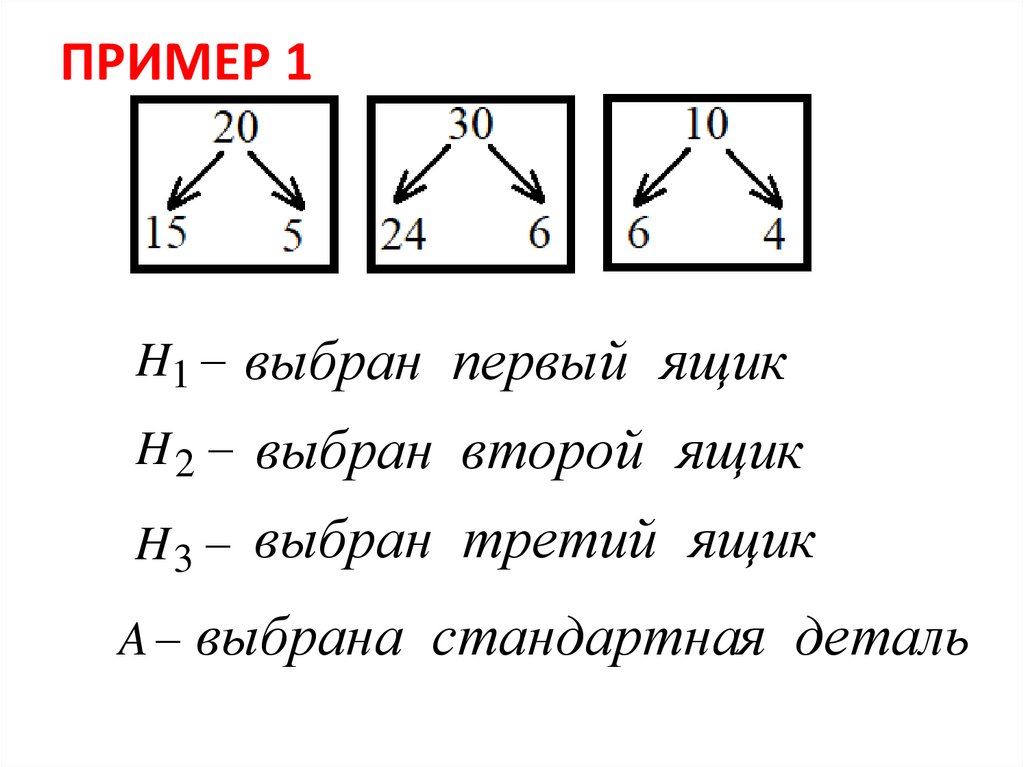
ПРИМЕР 1
В первом ящике содержится 20 деталей, из
них 15 стандартных; во втором – 30 деталей,
из них 24 стандартных; в третьем – 10
деталей, из них 6 стандартных. Найти
вероятность того, что наудачу извлеченная
деталь из наудачу взятого ящика –
стандартна.

6.

ПРИМЕР 1
H1 выбран первый ящик
H 2 выбран второй ящик
H 3 выбран третий ящик
A выбрана стандартная деталь

7.

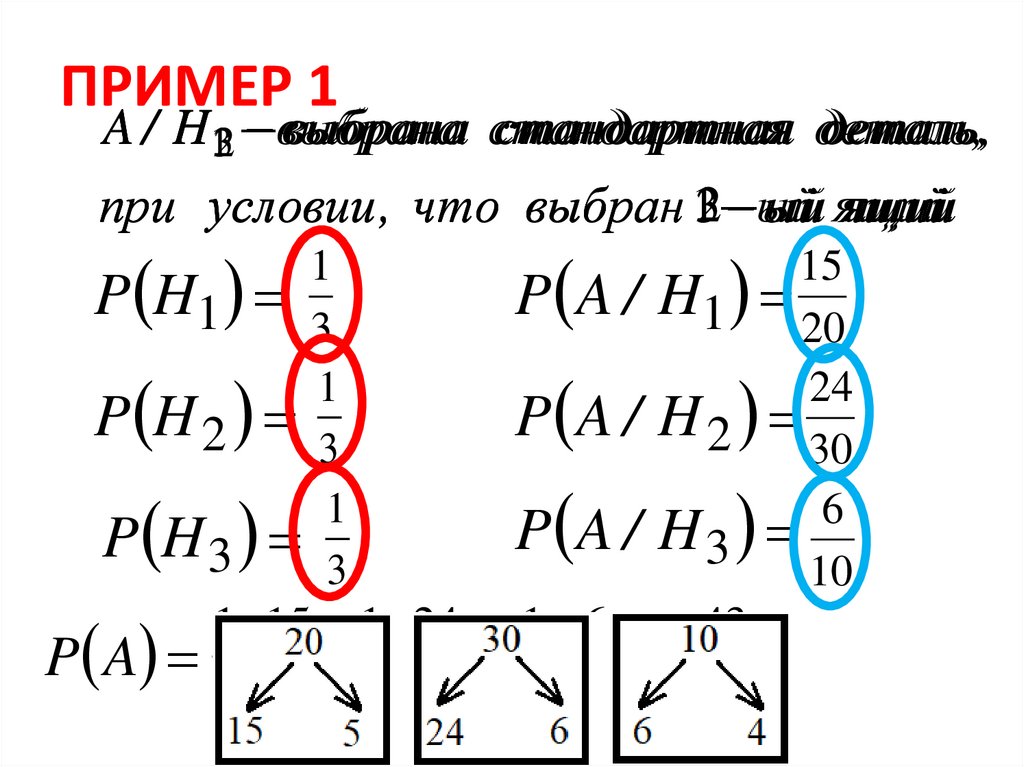
ПРИМЕР 1
выбрана стандартна
стандартнаяя деталь
деталь,,
A / H132 выбрана
при условии , что выбран 132 ый
ый ящий
ящий
1
P H1 3
1
P H2 3
1
P H3 3
15
P A / H1 20
24
P A / H 2 30
6
P A / H3
10
1 15 1 24 1 6
43
.
P A
3 20 3 30 3 10
60

8.

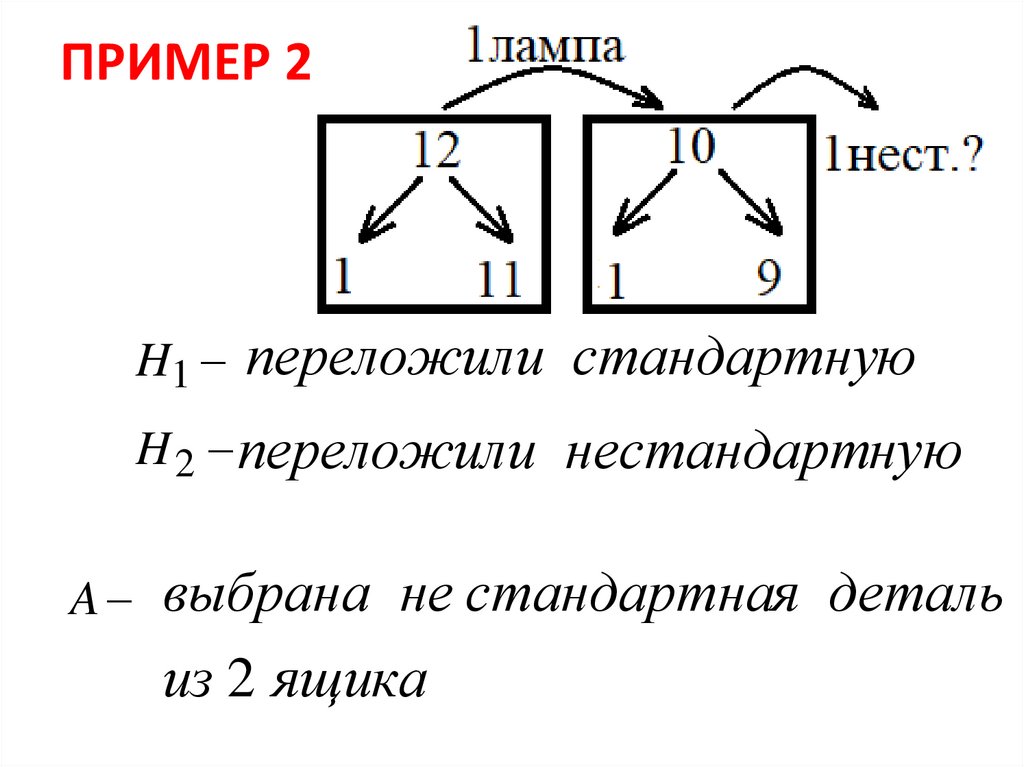
ПРИМЕР 2
В двух ящиках имеются радиолампы. В
первом ящике содержится 12 ламп, из них 1
нестандартная, во втором – 10 ламп, из них
тоже одна нестандартная. Из первого ящика
наудачу взята лампа и переложена во второй.
Найти вероятность того, что наудачу
извлеченная из второго ящика лампа будет
нестандартной.

9.

ПРИМЕР 2
H1 переложили стандартную
H 2 переложили нестандартную
A выбрана не стандартная деталь
из 2 ящика

10.

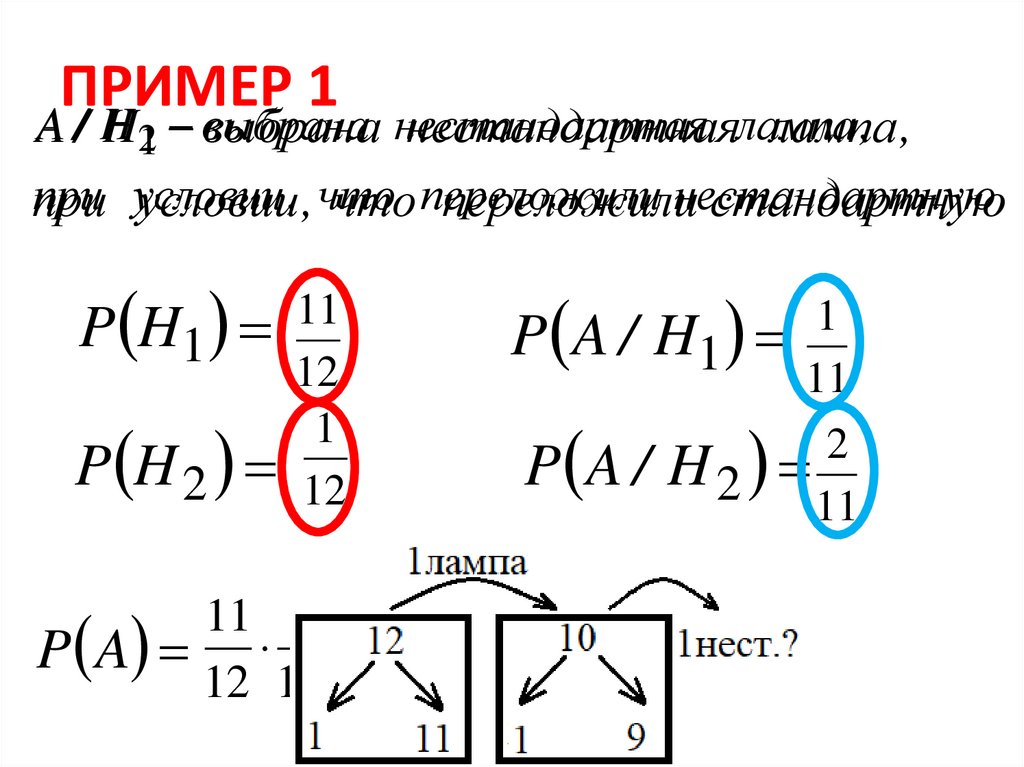
ПРИМЕР 1
A/ H
ная
, ,
H21 выбрана
выбрана нестандарт
нестандарт
наялампа
лампа
при условии
ную
условии, , что
что переложили
переложилинестандарт
стандартну
ю
P H1 11
12
1
P H 2 12
1
P A / H1
11
2
P A / H2
11
11 1 1 2 13
.
P A
12 11 12 11 132

11.

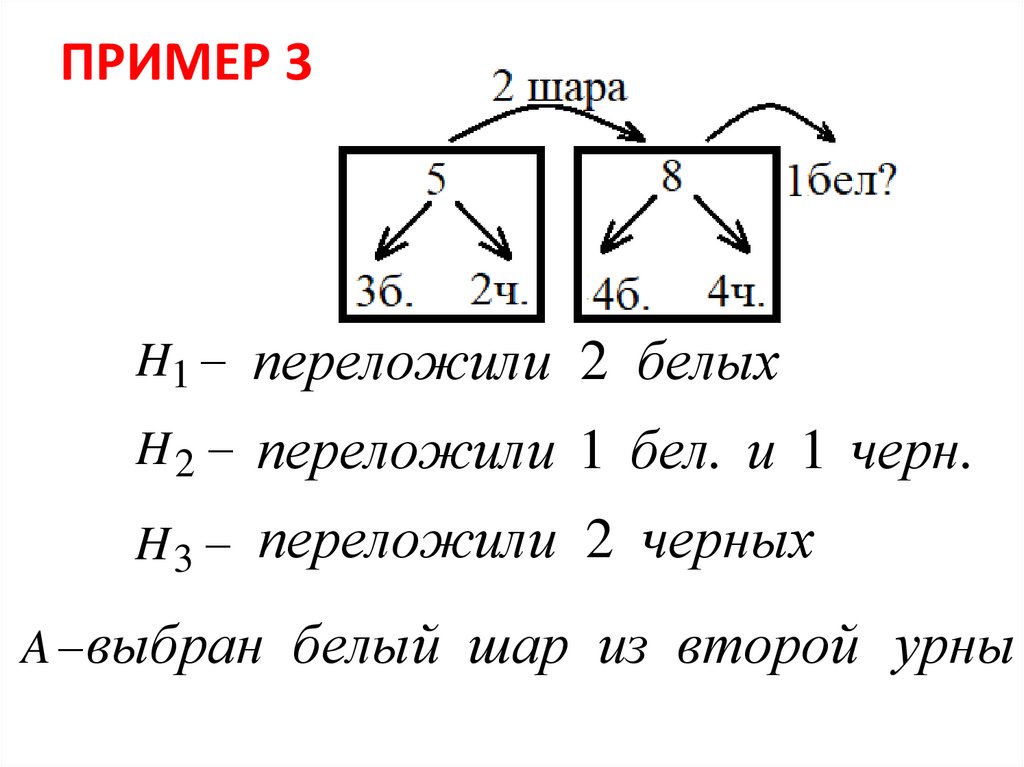
ПРИМЕР 3
Из урны, содержащей 3 белых и 2 черных
шара, переложили в урну с 4 белыми и 4
черными шарами 2 шара. После чего из
второй урны вынули один шар. Какова
вероятность того, что вынутый шар оказался
белым.

12.

ПРИМЕР 3
H1 переложили 2 белых
H 2 переложили 1 бел. и 1 черн.
H 3 переложили 2 черных
A выбран белый шар из второй урны

13.

ПРИМЕР 3
H312 выбран
из
урны
AA // H
, ,,
выбран белый
белый шар
шар из
из2 22урны
урны
при условии
условии,, что
что переложили
переложили 122бчерных
.белых
и 1 ч.
при
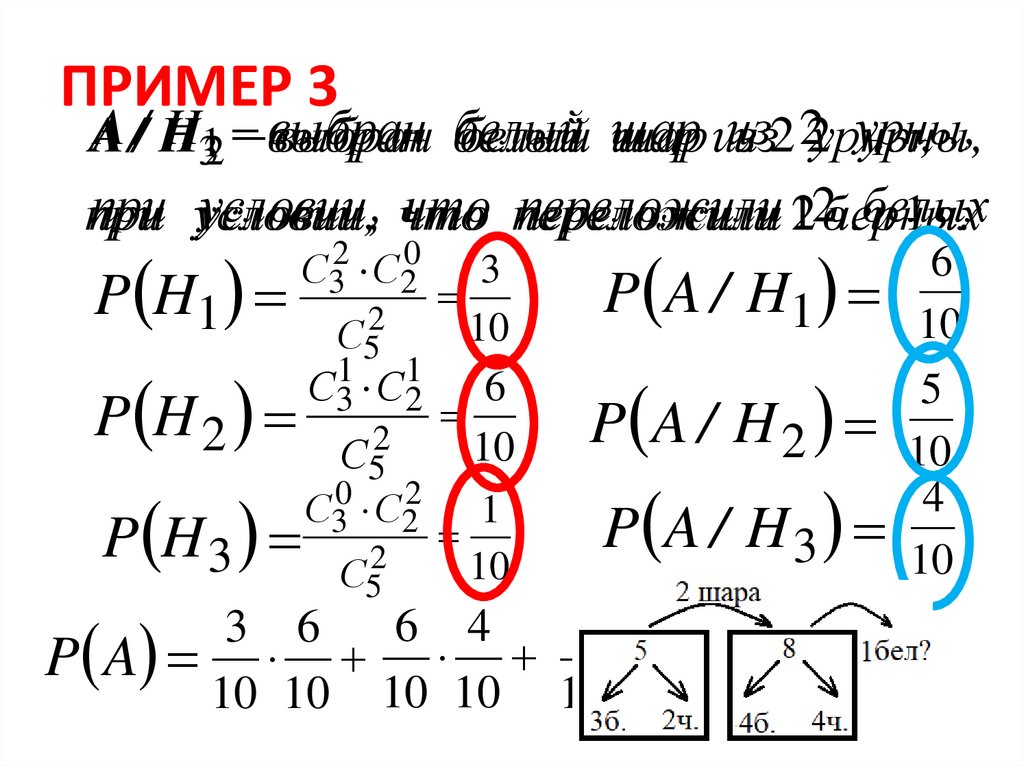
С32 С20
3
P H1 2 10
С5
С31 С12 6
P H 2 2 10
С5
С30 С22 1
P H 3 С 2 10
5
6
P A / H1 10
5
P A / H 2 10
4
P A / H 3 10
6 4
3 6
1 4
52
.
P A
10 10 10 10 10 10
100

14.

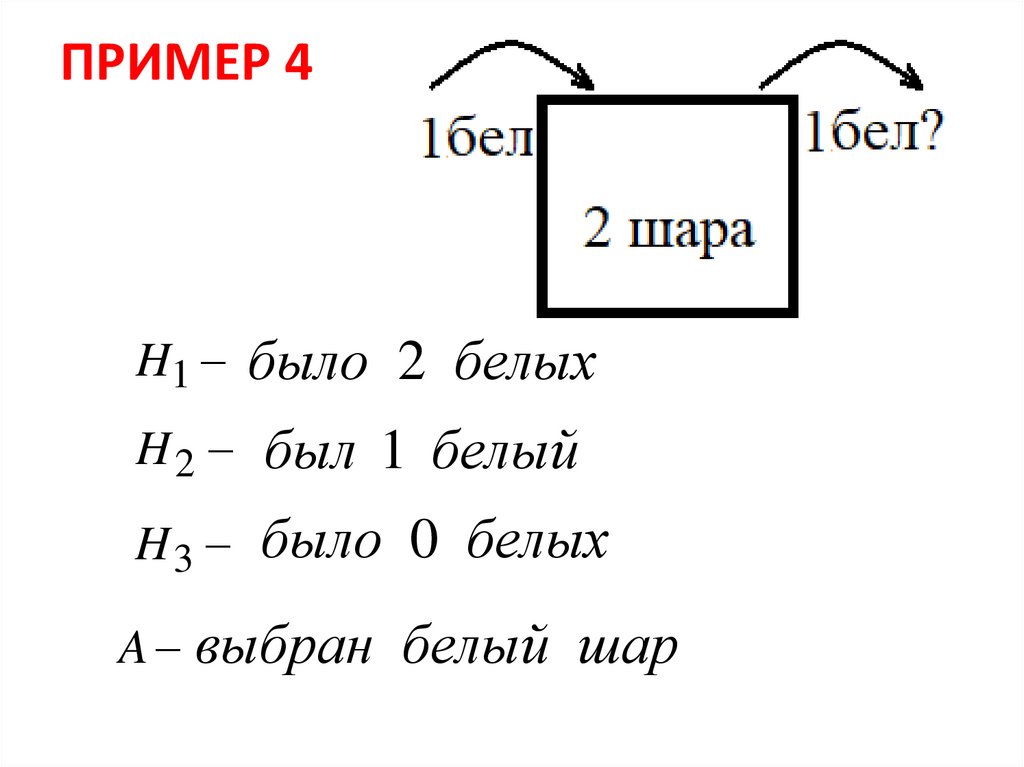
ПРИМЕР 4
В урну, содержащую два шара, опущен белый
шар. После чего из нее наудачу извлечен шар.
Найти вероятность того, что извлеченным
окажется белый, если равновероятны все
возможные предположения о
первоначальном составе шаров (по цвету)

15.

ПРИМЕР 4
H1 было 2 белых
H 2 был 1 белый
H 3 было 0 белых
A выбран белый шар

16.

ПРИМЕР 4
выбран белый
белый шар
шар,,
A
A // H
H213 выбран
при
при условии
условии,, что
что был
было1 белый
белых
02белых
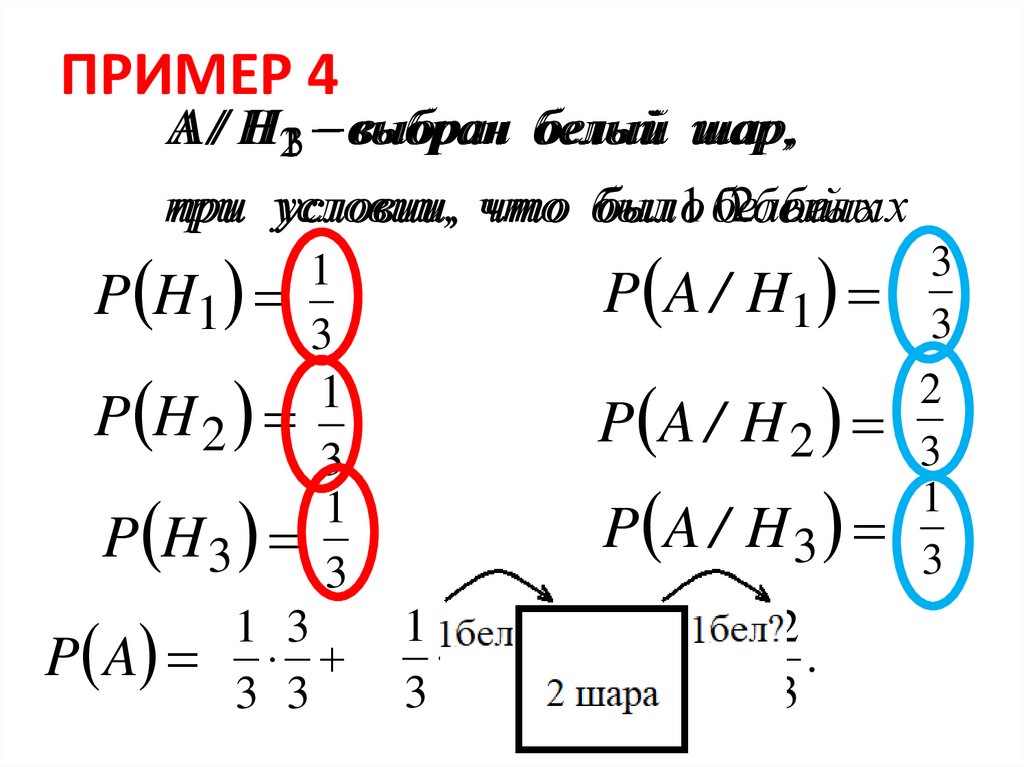
1
P H1
3
P A / H1
1
P H2
3
1
P H3
3
1 3
P A
3 3
P A / H 2
P A / H 3
1 2
3 3
1 1
3 3
2
.
3
3
3
2
3
1
3

17.

ПРИМЕР 5
В специализированную больницу поступает в
среднем 50% больных с заболеванием K, 30%
– с заболеванием L, 20% – с заболеванием М.
Вероятность полного излечения болезни K
равна 0,7; болезни L – 0,8; болезни М – 0,9.
Больной, поступивший в больницу, был
выписан здоровым. Найти вероятность того,
что этот больной страдал заболеванием K.

18.

ПРИМЕР 5
H1 AAпоступил
H213 больной
выписан
,,
с болезнью
K
больной
выписан здоровым
здоровым
// H
при
условии,с, что
что
страдал
болезнью LK
поступил
болезнью
L болезнью
H 2 при
условии
страдал
М
H 3 поступил с болезнью М
A
больной выписан здоровым
P H1 0,5
P H 2 0,3
P H 3 0,2
P A / H1 0,7
P A / H 2 0,8
P A / H 3 0,9

19.

ПРИМЕР 5
P H1 / A
0,5 0,7
0,5 0,7 0,3 0,8 0,2 0,9
5 7
35
5 7 3 8 2 9 77

20.

ПРИМЕР 6
Два автомата производят одинаковые детали,
которые поступают на общий конвейер.
Производительность первого автомата вдвое
больше производительности второго.
Первый автомат производит в среднем 60%
деталей отличного качества, а второй – 80%.
Наудачу взятая с конвейера деталь оказалась
отличного качества. Найти вероятность того, что
эта деталь произведена вторым автоматом.

21.

ПРИМЕР 6
A / H12 деталь
детальстандартна
стандартна, ,
условии
она
условии,, что
что
онаизготовлен
изготовленаа
H1 детальпри
изготовлен
а 1ым
автоматом
12ым
ымавтоматом
автоматом
H 2 деталь изготовлена 2ым автоматом
A наудачу взятая деталь стандартна
P H1 2 / 3
P H 2 1 / 3
P A / H1 0,6
P A / H 2 0,8
2 :1 2 1 3 2 / 3 и 1 / 3

22.

ПРИМЕР 6
P H 2 / A
1
3
2 6
3 10
8
10
1
3
8
10
1 8
8 2
2 6 1 8 20 5

23.

ПРИМЕР 7
Две перфораторщицы набили по
одинаковому комплекту перфокарт.
Вероятность того, что первая
перфораторщица допустит ошибку, равна
0,05. Для второй перфораторщицы эта
вероятность равна 0,1. При сверке перфокарт
была обнаружена ошибка. Найти вероятность
того, что ошиблась первая перфораторщица.

24.

ПРИМЕР 7
H21 перфокарта
AA// H
перфокартассошибкой
ошибкой, ,
принабивала
условии , что
ее набивала
при
условии
набивала щица
H1 перфокарту
1ая перфоратор
21ая перфоратор
перфораторщица
щица
H 2 перфокарту набивала 2ая перфораторщица
A наудачу взятая перфокарта с ошибкой
P H1 1 / 2
P H 2 1 / 2
P A / H1 0,05
P A / H 2 0,1
1:1 1 1 2 1 / 2 и 1 / 2

25.

ПРИМЕР 7
P H1 / A
1
2
1 5
2 100
5
100
1
2
10
100
1 5
5 1
1 5 1 10 15 3

26.

ПРИМЕР 8
При хороших метеоусловиях вероятность
благополучной посадки самолета равна
0,9999, при плохих – 0,9991. Для данного
аэропорта в 80 % случаев погода считается
летной. Найти вероятность благополучного
приземления самолета.

27.

ПРИМЕР 8
A / H12 самолет
самолет благополуч
благополунно
о приземлилс
приземлилсяя ,
H1 погода
летная
при условии , что
что погода
погодалетная
нелетная
H 2 погода нелетная
A благополуное приземление самолета
P H1 0,8
P H 2 0,2
P A / H1 0,9999
P A / H 2 0,9991
Найти вероятность благополучного приземления самолета.
8 9999 2 9991
PA
0,99974.
10 10000 10 10000

28.

ПРИМЕР 9
На предприятии установлена система
аварийной сигнализации. Когда возникает
аварийная ситуация, звуковой сигнал
появляется с вероятностью 0,95. Однако
сигнал может возникнуть и без аварийной
ситуации с вероятностью 0,001. Реальная
вероятность аварийной ситуации равна 0,005.
Чему равна вероятность аварийной ситуации,
если сигнализация сработала?

29.

ПРИМЕР 9
A / H12 сигнализац
сигнализация
иясработала
сработала,,
H1 есть аварийная
ситуация
при условии
, что есть
нет
аварийная
ситуация
аварийной
ситуации
H 2 нет аварийной
ситуации
A сигнализация сработала
P H1 0,005
P H 2 1 0,005 0,995
P A / H1 0,95
P A / H 2 0,001

30.

ПРИМЕР 9
P H1 / A
0,005 0,950
0,005 0,950 0,995 0,001
5 950
4750
0 ,83
5 950 995 1 5745

31.

ПРИМЕР 10
В данный район изделия поставляются тремя
фирмами в соотношении 5:8:7. Среди продукции
первой фирмы стандартные изделия составляют
90 %, второй – 85 %, третьей – 75 %.
а) Найти вероятность того, что приобретенное
изделие окажется нестандартным.
б) Приобретенное изделие оказалось
стандартным. Какова вероятность того, что оно
изготовлено третьей фирмой?

32.

ПРИМЕР 10
1ой фирмой
H1 изделие
A /поставлено
H изделие
изделие
стандартноее,,
стандартно
123
H 2 изделие поставлено 2ой фирмой
при условии , что оно
H 3 изделие поставлено 3ой фирмой
А
поставлено
2
1
3
ой
ой
фирмой
фирмой
изделие стандартно
P H1 5
P A / H1 0,9
8
P H 2
20
P A / H 2 0,85
20
7
P H 3
20
P A / H 3 0,75
5 : 8 : 7 5 8 7 20 5/20, 8/20, 7/20

33.

ПРИМЕР 10
P H1 5
20
P A / H1
0,9
8
P H 2
20
P A / H 2 0,85
7
P H 3
20
P A / H 3
0,75
5 90
8 85
7 75 1655
.
P A 20 10 20 100
20 100 2000
1655 345
Р А 1
.
2000 2000

34.

ПРИМЕР 10
P H 3 / A 5
20
7
20
75
100
90
8 85 7
100
20 100 20
75
100
7 75
525
5 90 8 85 7 75 1655