Умозаключение как форма мышления. Особенности применения умозаключений в юридической деятельности

1.

1.
2.
3.
4.
5.
6.
7.
План
Дедуктивные умозаключения и их виды
Непосредственные умозаключения
Простой категорический силлогизм
Опосредованные
умозаключения,
основанные на связях между высказываниями
Понятие и виды индуктивных умозаключений
Методы установления причинных связей
Умозаключения по аналогии

2.

Рассуждение – это ряд суждений, которые
относятся к определенному вопросу или
предмету, следуют один за другим
таким образом, что из предшествующих
суждений с необходимостью следуют
другие, а в результате получается
единственно правильный ответ на
поставленный вопрос.
Умозаключение – это способ получения
нового знания на основе некоторого
имеющегося

3.

Идеалистический взгляд на умозаключение – исходит из
того, что умозаключение является чисто субъективной
сущностью как по содержанию, так и по структуре.
Материалистический взгляд на умозаключение - исходит
из понимания его содержания как отражения реальных
связей, свойств и отношений.
В содержательных умозаключениях прослеживается связь
между
ситуациями
действительности,
которые
представляют
эти
высказывания.
Переход
от
содержательного
умозаключения
к
формальному/формализация/
осуществляете
посредством выявления и фиксации всей информации,
которая используется в содержательном рассуждении.
Логическое следствие из посылок – это суждение, которое
не может быть ложным, если эти посылки истинны.

4.

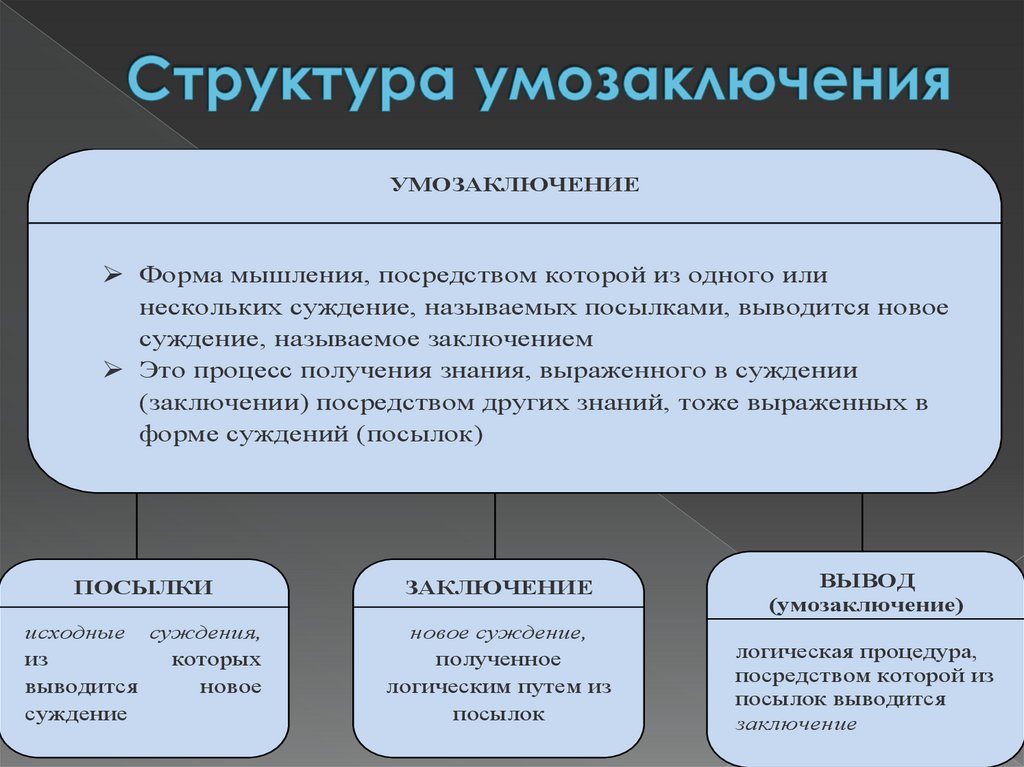
УМОЗАКЛЮЧЕНИЕ
Форма мышления, посредством которой из одного или
нескольких суждение, называемых посылками, выводится новое
суждение, называемое заключением
Это процесс получения знания, выраженного в суждении
(заключении) посредством других знаний, тоже выраженных в
форме суждений (посылок)
ПОСЫЛКИ
ЗАКЛЮЧЕНИЕ
исходные суждения,
из
которых
выводится
новое
суждение
новое суждение,
полученное
логическим путем из
посылок
ВЫВОД
(умозаключение)
логическая процедура,
посредством которой из
посылок выводится
заключение

5.

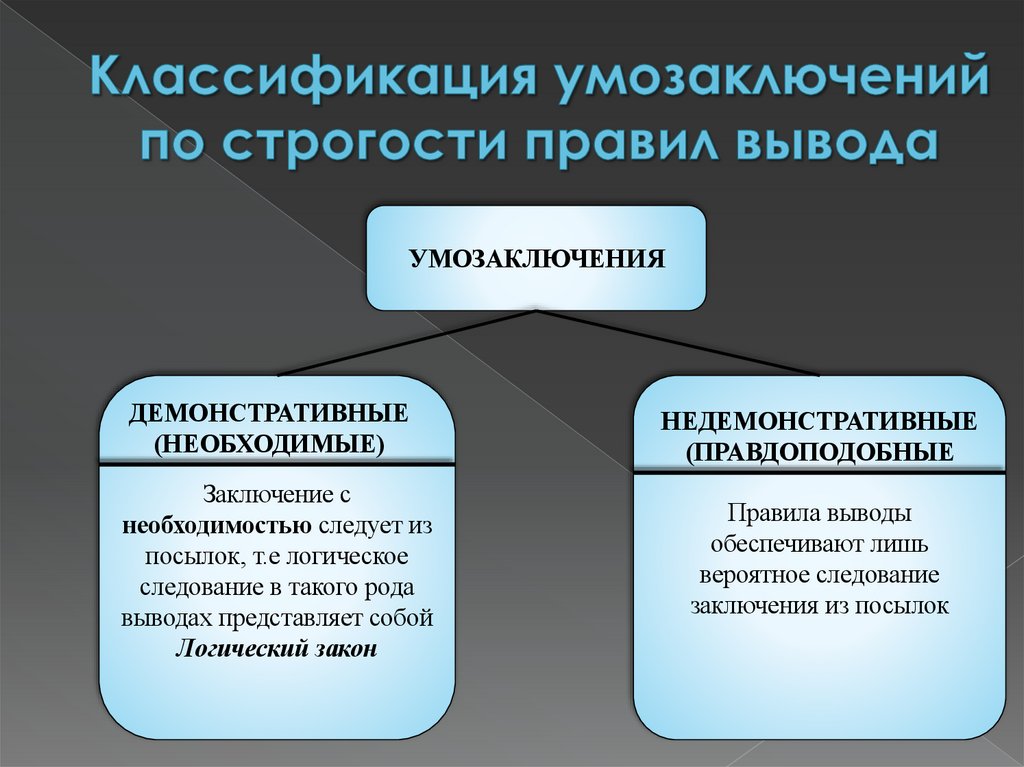
УМОЗАКЛЮЧЕНИЯ
ДЕМОНСТРАТИВНЫЕ
(НЕОБХОДИМЫЕ)
НЕДЕМОНСТРАТИВНЫЕ
(ПРАВДОПОДОБНЫЕ
Заключение с
необходимостью следует из
посылок, т.е логическое
следование в такого рода
выводах представляет собой
Логический закон
Правила выводы
обеспечивают лишь
вероятное следование
заключения из посылок

6.

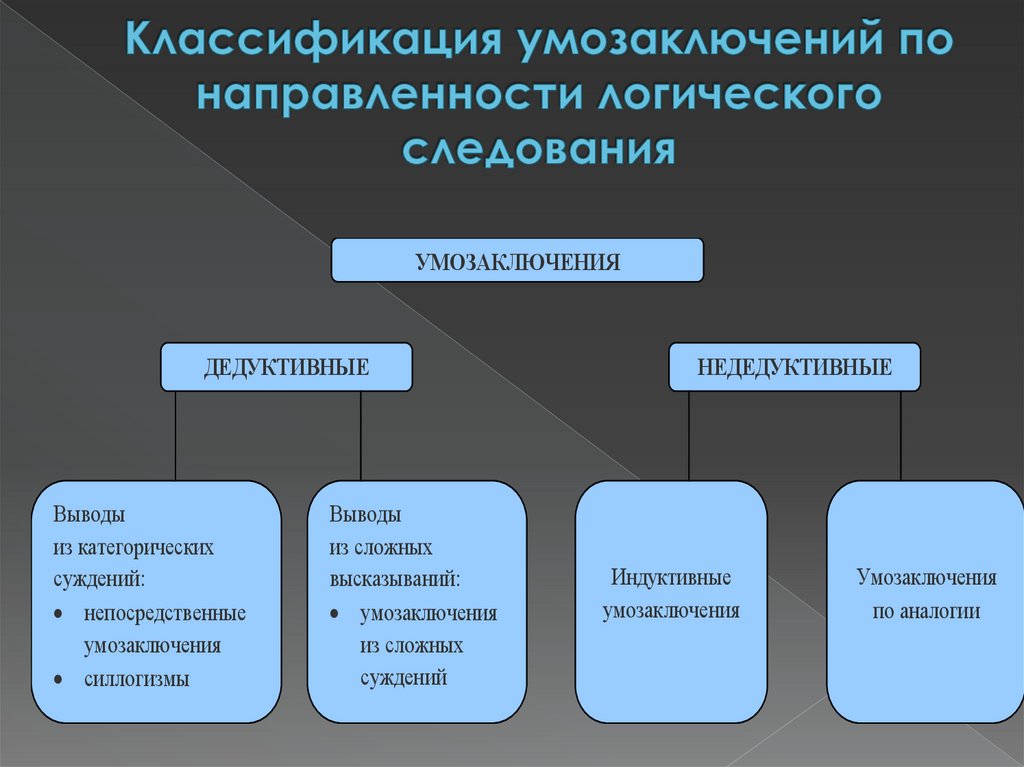
УМОЗАКЛЮЧЕНИЯ
ДЕДУКТИВНЫЕ
Выводы
из категорических
суждений:
непосредственные
умозаключения
силлогизмы
Выводы
из сложных
высказываний:
умозаключения
из сложных
суждений
НЕДЕДУКТИВНЫЕ
Индуктивные
умозаключения
Умозаключения
по аналогии

7.

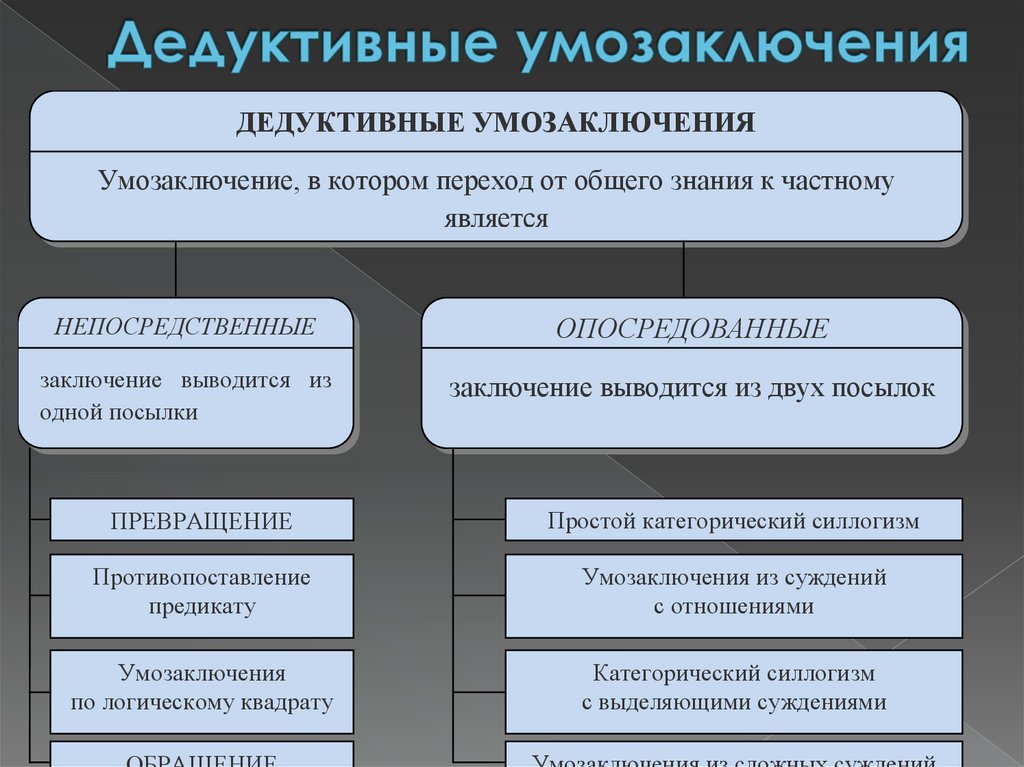
ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ
Умозаключение, в котором переход от общего знания к частному
является
логически необходимым
НЕПОСРЕДСТВЕННЫЕ
ОПОСРЕДОВАННЫЕ
заключение выводится из
одной посылки
заключение выводится из двух посылок
Противопоставление
предикату
Простой категорический силлогизм
предикату
Умозаключения из суждений
с отношениями
Умозаключения
по логическому квадрату
Категорический силлогизм
с выделяющими суждениями
ПРЕВРАЩЕНИЕ

8.

Непосредственные умозаключения - такие, которые выводятся из
одной посылки, являющейся категорическим суждением.
Превращение - преобразование суждения в суждение, в результате
которого
меняется
качество
исходного
суждения
с
одновременной заменой его предиката на противоречащее
понятие.
Схема превращения
S есть P
S не есть не - P
Превращению подлежат суждения A,E,I,O:
A→E
E→A
Все S есть P
Ни одно S не есть не - P
Ни одно S не есть P
Все S есть не-P
Пример: Ни один кит не есть рыба
Все киты есть не - рыба
Пример: Все тигры - хищные животные
Ни один тигр не является
нехищным животным
I→O
O→I
Некоторые S есть P
Некоторые S не есть не - P
Пример: Некоторые металлы являются
жидкими
Некоторые металлы не
Некоторые S не есть P
Некоторые S есть не - P
Пример: Некоторые студенты не
являются отличниками
Некоторые студенты

9.

Обращение – преобразование суждения, в результате которого субъект
исходного суждения становиться предикатом, а предикат – субъектом
заключения.
S есть P
P есть S
Обращению подлежат суждения A,E,I:
A→I
I→I
Е→ Е
Все S есть P
Некоторые P есть S
Некоторые S есть P
Некоторые P есть S
Ни одно S не есть P
Ни одно P не есть S
Пример.
Все рыбы дышат
жабрами
Некоторые дышащие
жабрами существа есть
рыбы
Пример.
Некоторые металлы - жидкости
Некоторые жидкости - металлы
Пример.
Ни один кит не является
рыбой
Ни одна рыба не есть
кит
Общеутвердительные
выделяющие
суждения
Частноутвердительные
выделяющие
суждения
Частноотрицательное
суждение (O)
Все S, и только S, есть P
Некоторые S, и только S, есть P
Все P есть S
Все P есть S
не обращается

10.

Противопоставление предикату - это преобразование суждения, в
результате которого субъектом становиться понятие, противоречащее
предикату, а предикатом – субъект исходного суждения; связка
меняется на противоположную.
Противопоставлению предикату подлежат суждения A,E,O:
A→E
E→ I
Все S есть P
Ни одно не – P не есть S
Ни одно S не есть P
Некоторые не – P есть S
Пример.
Все металлы электропроводны
Ни один не-электропроводник не
является металлом
Пример.
Ни одна бледная поганка не является
съедобным грибом
Некоторые несъедобные грибы есть
бледные поганки
O→I
Частноутвердительные суждения (I)
посредством противопоставления
предикату не преобразуется
Некоторые S не есть P
Некоторые не –P есть S
Пример.
Некоторые преступления не являются
умышленными
Некоторые неумышленные деяние
являются преступлениями

11.

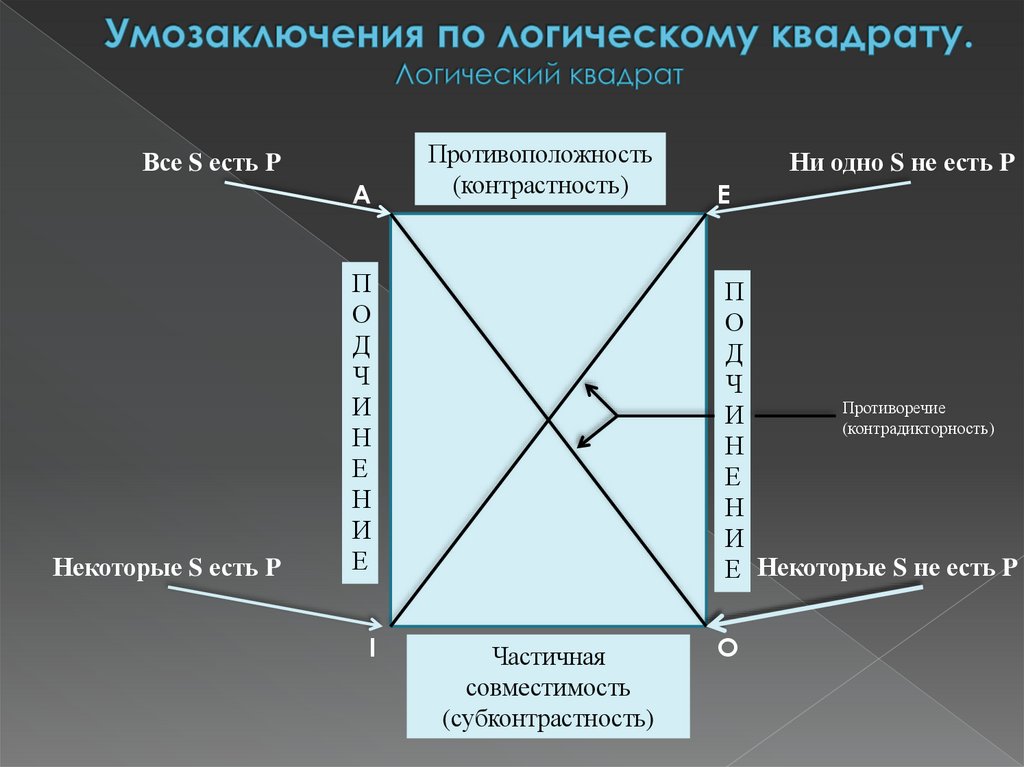
Все S есть P
A
Некоторые S есть P
Противоположность
(контрастность)
П
О
Д
Ч
И
Н
Е
Н
И
Е
I
Ни одно S не есть P
E
П
О
Д
Ч
Противоречие
И
(контрадикторность)
Н
Е
Н
И
Е Некоторые S не есть P
Частичная
совместимость
(субконтрастность)
O

12.

ОТНОШЕНИЕ ПРОТИВОРЕЧИЯ (КОНТРАДИКТОРНОСТИ) A – O, E – I
Из истинности одного суждения следует ложность другого суждения, из ложности одного – истинность
другого
Выводы строятся по схемам: A →˥ O; ˥A→ O ; E →˥ I ; ˥E→ I
ОТНОШЕНИЕ ПРОТИВОПОЛОЖНОСТИ (КОНТРАДИКТОРНОСТИ) A – E
Из истинности одного суждения следует ложность другого суждения, но из ложности одного из них не
следует истинность другого
Выводы строятся по схемам: A →˥E; E→˥A ; ˥A →(E v ˥E); ˥E→ (A v ˥A)
ОТНОШЕНИЕ ЧАСТИЧНОЙ СОВМЕСТИМОСТИ (СУБКОНТРАСТНОСТИ) I – O
Истинными могут быть оба суждения, но не могут быть вместе ложными, по крайней мере, одно из них истинно. Из ложности
одного суждения следует истинность другого, но из истинности одного из них может следовать как истинность, так и ложность
другого суждения
Выводы строятся по схемам: ˥I →O; ˥O → I; I→ (O v ˥O); O→ ( I v ˥I )
ОТНОШЕНИЕ ПОДЧИНЕНИЯ A – I, E – O
Из истинности подчиняющего суждения следует истинность подчиненного суждения, но не наоборот: из истинности
подчиненного суждения истинность подчиняющего суждения не следует, оно может быть истинным, но может быть и ложным
Выводы строятся по схемам: A → I; E→O; I→ (A v ˥A); O→ (E v ˥E); ˥ I→ ˥A); ˥ O→˥E;
˥A→ (I v ˥I); ˥E→ (O v ˥O)