Similar presentations:
Решение иррациональных уравнений
1. Решение иррациональных уравнений
2.
Ощущение тайны – наиболее прекрасноеиз доступных нам переживаний. Именно
это чувство стоит у колыбели
истинного искусства и настоящей науки.
А .Эйнштейн
3. - какое число?
IгII г
III г
IV г
X0 =27
X0 = 36
X0=8
X0 =
2=x²
- какое число?
• Избавьтесь от иррациональности
4.
Удивительное открытие пифагорийцев.Каким числом выражается длина диагонали квадрата со
стороной 1?
С латыни слово «irrationalis» означает «неразумный».
«surdus» - «глухой» или «немой»
5.
ПОНЯТИЕ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯЕсли в уравнении переменная содержится
под знаком квадратного корня, то
уравнение называют иррациональным.
Примеры:
2x 1 3
2x 5 4x 7
2 x 5x 2 x 6
2
6.
Выбрать иррациональноеуравнение:
7.
Основные методы решенияиррациональных уравнений:
возведение в степень обеих частей
уравнения;
введение новой переменной;
метод анализа уравнения.
8.
Метод возведения в квадрат обеих частейуравнения
Пример №1
2x 1 3
2x 1 3
2
2x 1 9
2x 8
x 4
Ответ: x 4
9.
Метод возведения в квадрат обеих частейуравнения
Пример №2
2x 5 4x 7
( 2x 5) ( 4x 7 )
2
2x 5 4x 7
x 1
Проверим!!!
2
10.
ПРОВЕРКАПодставим 1 вместо х в заданное
иррациональное уравнение, получим:
2 1 5 4 1 7
3 3
x 1 - посторонний корень
Ответ: иррациональное уравнение не
имеет корней
11.
ЗАПОМНИ1) Возвести обе части уравнения
в квадрат.
2) Обязательно сделать
проверку!!!
12.
Метод возведения в степеньобеих частей уравнения:
1) Если иррациональное уравнение содержит
только один радикал, то нужно записать
так, чтобы в одной части знака равенства
оказался только этот радикал. Затем обе
части уравнения возводят в одну и ту же
степень, чтобы получилась рациональное
уравнение.
13.
Метод возведения в степеньобеих частей уравнения:
2)
Если в иррациональном уравнении
содержится два или более радикала, то
сначала изолируется один из радикалов,
затем обе части уравнения возводят в одну и
ту же степень, и повторяют операцию
возведения в степень до тех пор, пока не
получится рациональное уравнение.
14.
f ( x) g ( x)f ( x) g ( x)
g ( x) 0
f ( x) g ( x)
f ( x) g ( x)
f ( x) 0( g ( x) 0)
2
15.
Решите устнох 16 1
х 17
25 х 10
х 4
2
16.
Решите устнох 5
10
х
7 х 1 3
7
2
х 1, х 4
х 5х 4 0
х 1 2
2
17.
ТРЕНИРУЕМСЯ РЕШАТЬ1)
х 2 3
х 2 3
2
х 2 9
х 7.
Проверка :
7 2 3
9 3
3 3 верно
2)
2
6 5х 2
2
6 5х 2
2
2
6 5х 2 4
2
2
х .
3
Корней нет
2
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
Метод введения новой переменнойДанный метод применяется в том
случае, когда в уравнении неоднократно
встречается
некоторое
выражение,
зависящее от неизвестной величины. Тогда
имеет смысл принять это выражение за
новую переменную и решить уравнение
сначала
относительно
введенной
неизвестной, а потом найти исходную
величину.
28.
29.
Метод замены переменнойПример №10
2х х 3 0
Делаем замену :
х t
x t2
t 2 5t 6 0
D 25 24 49
t1 6, t 2 1
Подставляе м :
х -
6
посторонний
корень
х 1, х 1
Ответ : х 1
30.
31.
Метод анализа уравненияСвойства корней, которые используют при решении
уравнений данным способом:
1. Все корни четной степени являются арифметическими, то
есть если подкоренное выражение отрицательно, то
корень лишен смысла; если подкоренное выражение
равно нулю, то корень так же равен нулю; если
подкоренное выражение положительно, то значение
корня положительно.
2. Все корни нечетной степени определены при любом
значении подкоренного выражения.
3. Функции
y
2n
x
и
y
2 n 1
x
являются возрастающими в своей области определения.
32.
33.
34.
На домрешите уравнения
1). 5 х 16 х 2
2).
2 х 8 х 16 44 2 х
3).
3х 7 х 2 3
2
4). 2 х х 3 0
35.
Уравнения, в которых переменная содержится подзнаком корня, называются иррациональными.
При возведении обеих частей уравнения
• в четную степень (показатель корня – четное
число) – возможно появление постороннего корня
(проверка необходима).
• в нечетную степень (показатель корня – нечетное
число) – получается уравнение, равносильное
исходному (проверка не нужна).
Решая иррациональные уравнения с помощью
равносильных преобразований – проверка не нужна.













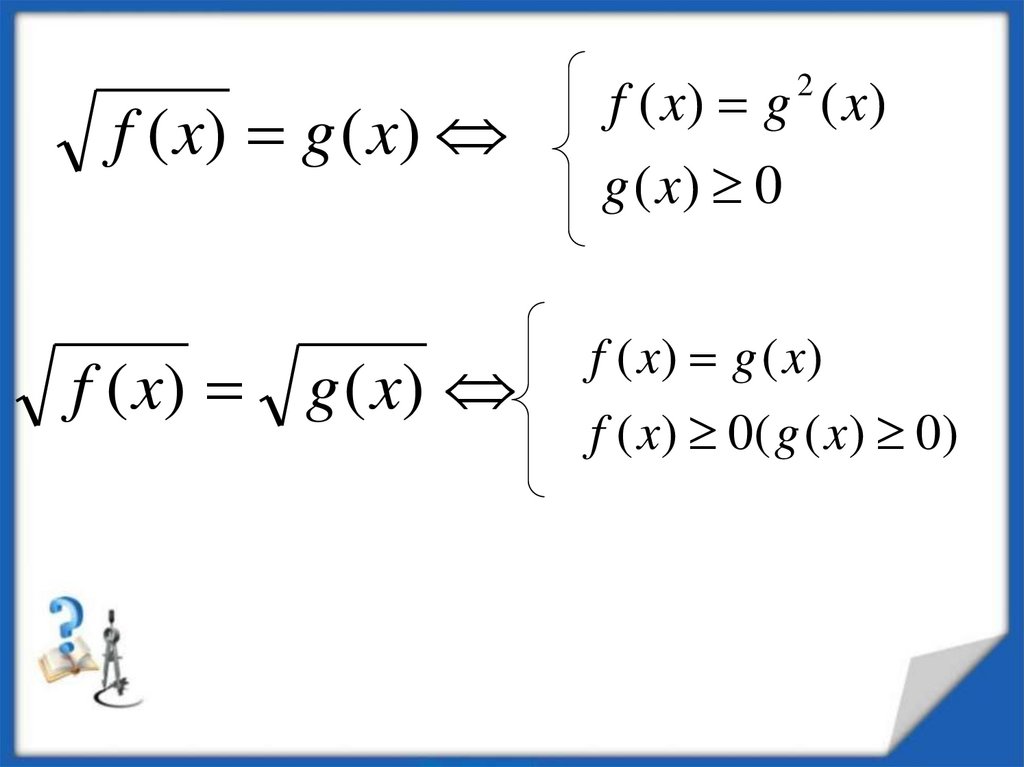





















 mathematics
mathematics








