Производная функции

1.

Производная
функции

2.

Лагранж Жозеф Луи
Лагранж Жозеф Луи (1736-1813) –
французский математик и механик, член
Берлинской и Парижской Академии наук.
Самостоятельной изучал математику, в 23 года
стал академиком. Сделал массу открытий.
Парижская АН пять раз присуждала ему
премии. В математике и механике его именем
названы несколько методов, формул и теорем.
Термин «производная» введен Лагранжем на
рубеже 18-19 веков. Производная –
произведенная, полученная по определенным
правилам из данной функции.

3.

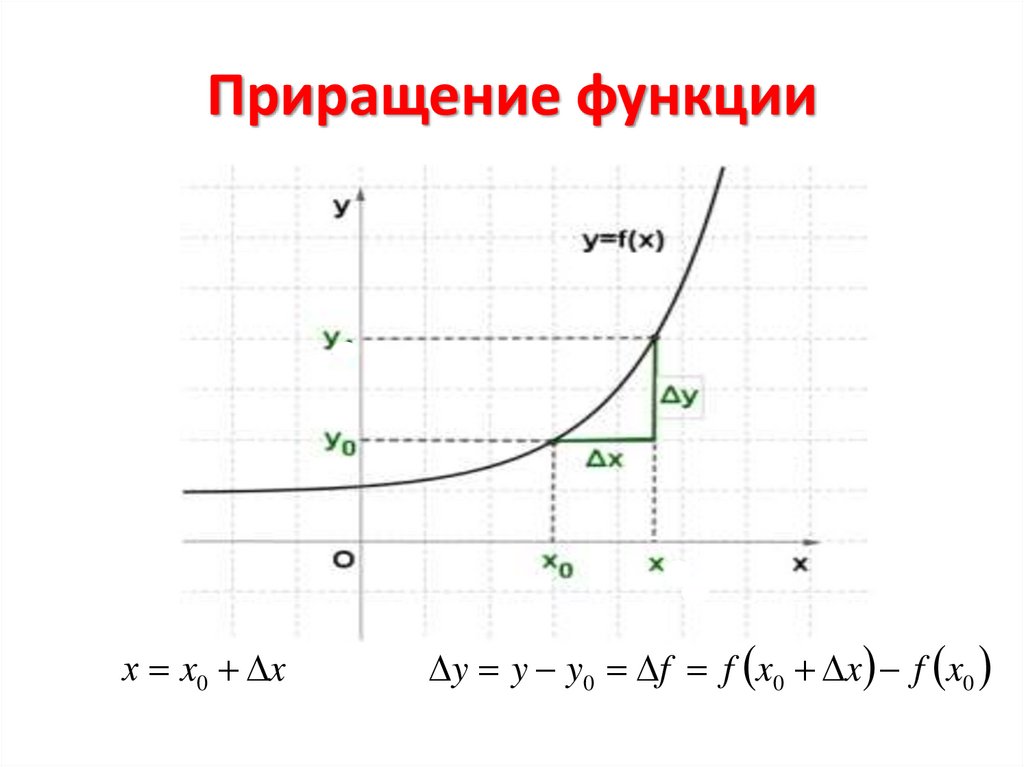
Приращение функции
Пусть дана функция y=f(x). Возьмем точку
х0єD(f).
Изучая поведение функции y=f(x) около
конкретной точки х0, важно знать, как
меняется значение функции при изменении
значения аргумента. Для этого используют
понятия приращений аргумента и функции.
• Разность x x x0 называется приращением
аргумента .
• Разность y f f х f x0 называется
приращением функции.

4.

Приращение функции
х x0 x
y y y0 f f x0 x f x0

5.

Примеры и разбор решения заданий
Пример 1.
Найдем приращение Δx и Δf в точке
2
X0, если f(x)= x , X0 =2 и X=1,9
Решение:
Δx=X- X0 =1,9-2=-0,1
2 2
Δf= f(1,9) –f(2)=1,9 -2 =-0,39
Ответ: Δx=-0,1; Δf =-0,39

6.

Примеры и разбор решения заданий
Пример 2.
Найдем приращение Δx и Δf в точке
2
X0, если f(x)=X , X0 =2 и х=2,1
Решение:
Δx= X- X0 =2,1-2=0,1
2 2
Δf= f(1,9) –f(2)=2,1 -2 =4,41-4=0,41
Ответ: Δx=0,1; Δf =0,41

7.

Примеры и разбор решения заданий
Пример 3.
1
f
x
Найдем приращение Δf функции
x
в точке X0,если приращение аргумента равно Δx.
Решение:
1
1
f f x0 x f x0
x0 x x0
x0 x0 x
x
x0 x0 x x0 x0 x
Ответ:
x
f
x0 x0 x

8.

Решите самостоятельно
Найдите приращение Δx и Δf в точке X0, если
1) f(x)= 2x2-3, X0 =3, x=2,8.
2) f(x)= 2x+1, X0 =5, x=4,99.
3) f(x)= 2x-3, X0 =-2, x=-1,9.
4) f(x)= 0,5x2, X0 =-2, x=-1,9.

9.

Ответы
1. -2,32
2. -0,02
3. 0,2
4. -0,195

10.

Физический смысл
• С помощью введенных обозначений
приращений удобно также выражать
среднюю скорость движения за
промежуток времени t0 ; t0 t .
Если точка движется по прямой и известна
ее координата x(t), то
x x t0 t x t0
vср t
t
t
• Эта формула верна и для ∆t<0 (для
промежутка t0 t ;t0 )

11.

Примеры и разбор решения заданий
Пример 4.
Точка движется по закону х(t)=2t-1. Найдите
среднюю скорость движения за промежуток
времени от t=0,8 до t=1.
Решение:
1).Найдем ∆t= 1-0,8=0,2
2). x t0 =х(0,8)= 2·0,8-1= 0,6
x t0 t = х(1)= 2·1-1= 1=х(t0+∆t)
x x t0 t x t0 1 0,6 0,4
vср t
2
t
t
0,2
0,2
• Ответ: 2.

12.

Решите самостоятельно
1).Точка движется по закону х(t)=3t+2
Найдите среднюю скорость
движения за промежуток времени
от t=0,5 до t=2.
2). Точка движется по закону
х(t)=3+12t-t2. Найдите среднюю
скорость движения за промежуток
времени от t=4 до t=5.

13.

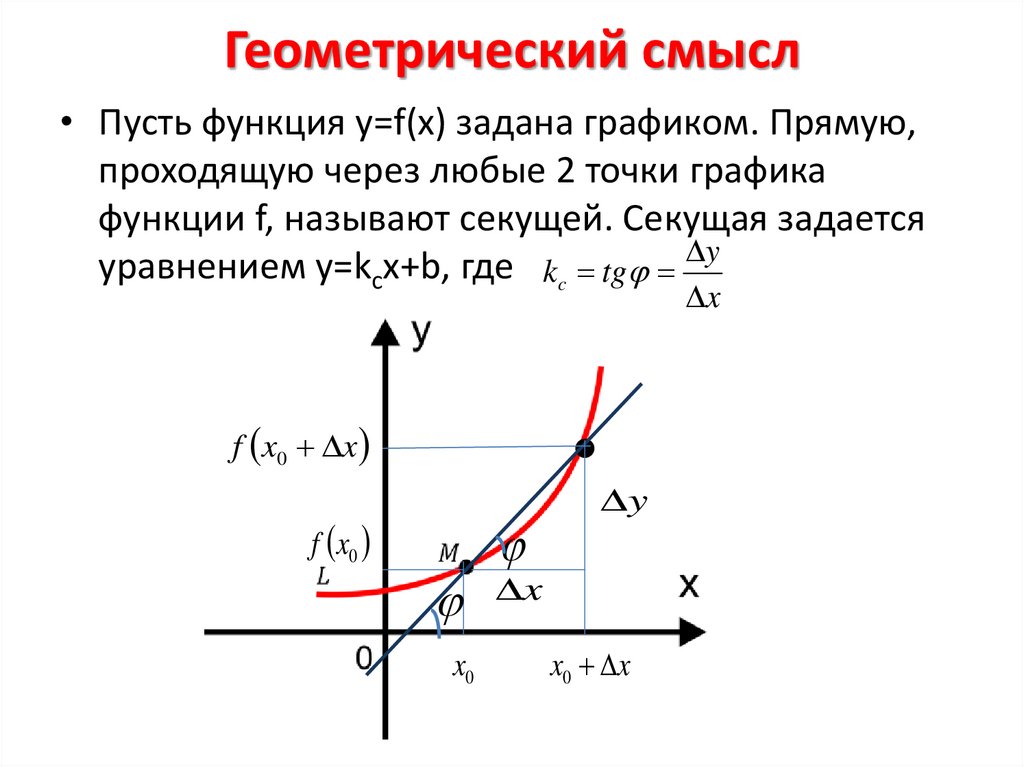
Геометрический смысл
• Пусть функция y=f(x) задана графиком. Прямую,
проходящую через любые 2 точки графика
функции f, называют секущей. Секущая задается
уравнением y=kсx+b, где kc tg y
x
f x0 x
f x0
x0
y
x
x0 x

14.

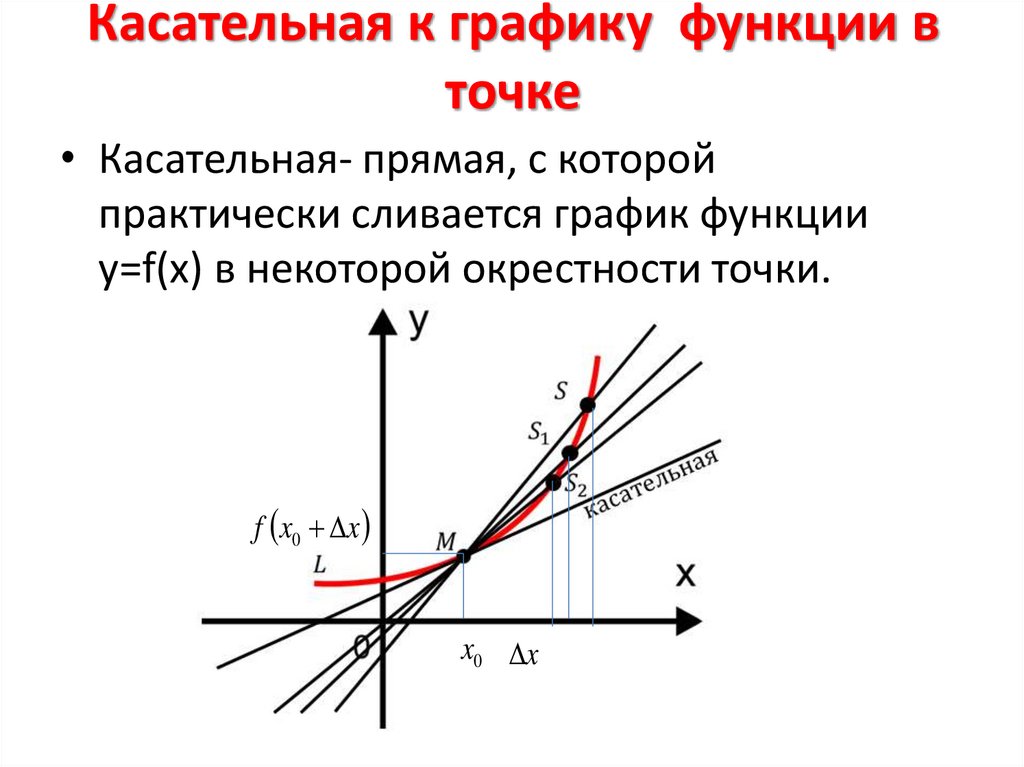
Касательная к графику функции в
точке
• Касательная- прямая, с которой
практически сливается график функции
y=f(x) в некоторой окрестности точки.
f x0 x
x0 x

15.

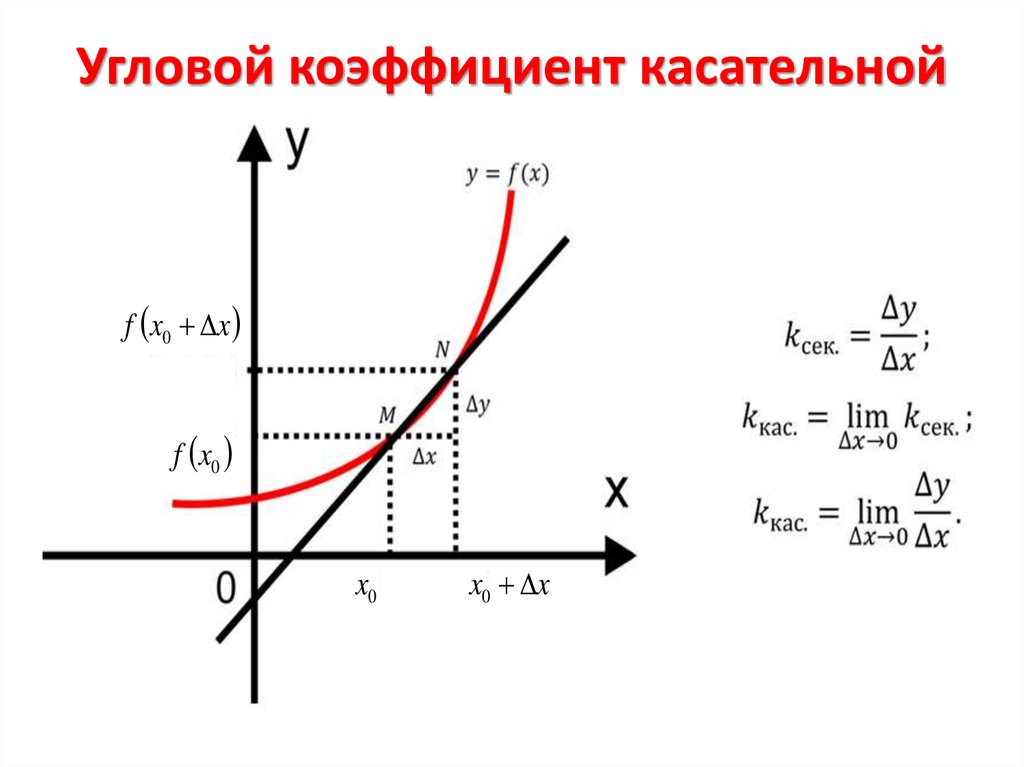
Угловой коэффициент касательной
f x0 x
f x0
x0
x0 x

16.

Определение производной
функции в точке
• Производной функции y = f (x) в точке х0
называется предел отношения приращения
функции к приращению аргумента при
∆х→0.
f x0 x f x0
у
у f x0 lim lim
x 0 x
x 0
x

17.

Дифференцирование
• Если функция f(x) имеет производную
в точке х, то эта функция называется
дифференцируемой в этой точке. Если
функция f(x) имеет производную в
каждой точке некоторого промежутка,
то эта функция дифференцируема на
этом промежутке. Операция
нахождения производной называется
дифференцированием.

18.

Алгоритм нахождения
производной функции в точке
1. Найти приращение функции
y f f х f x0
2. Найти предел отношения приращения функции к
приращению аргумента, когда приращение
аргумента стремится к нулю.
f x0 x f x
f
f ( x0 ) lim
lim
x 0 x
x 0
x

19.

Найти производную функции в
точке (по определению)
Пример 5.
f x kx b
1). f f х f x0
f x0 kx0 b
f kx b kx0 b kx b kx0 b
kx kx0 k x x0 k x
f
k x
2). f ( x0 ) lim
lim
k
x 0 x
x 0 x
kx b k

20.

Найдите производную функции в
точке (по определению)
1). f x 5 x 1
2). f x x
2

21.

Таблица производных
1. kx b k
2. x 1
3.C 0
2x
4. x
2