Производная. Вопросы для повторения

1. Производная

2. Вопросы для повторения

• Приращение аргумента. Приращение
функции. Геометрическая
иллюстрация.
• Секущая, её угловой коэффициент.
• Касательная. Угловой коэффициент
касательной.
• Определение производной функции в
точке.
• Как называют операцию нахождения
производной?

3. Геометрический смысл производной

Для функции y = f (x) ее производная y' = f '(x0)
в точке x0 равна угловому коэффициенту
(тангенсу угла наклона) касательной,
проведенной к графику функции в точке x0.
f
ксек lim
f x0
x 0 x
ксек tg
f x0 tg

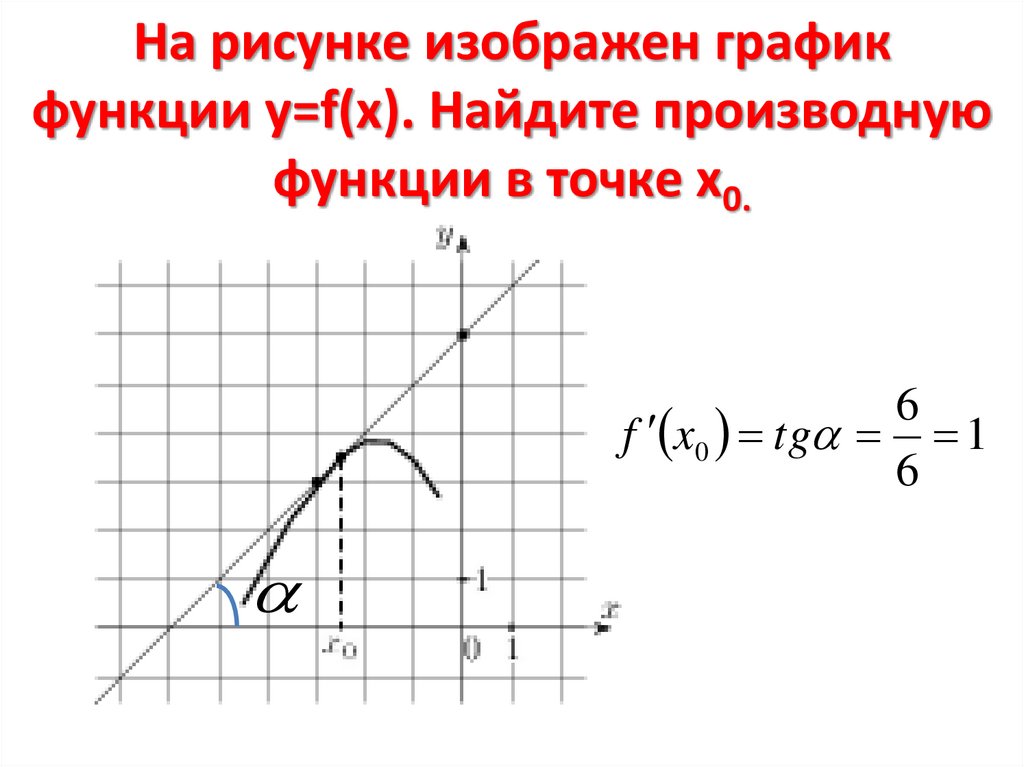
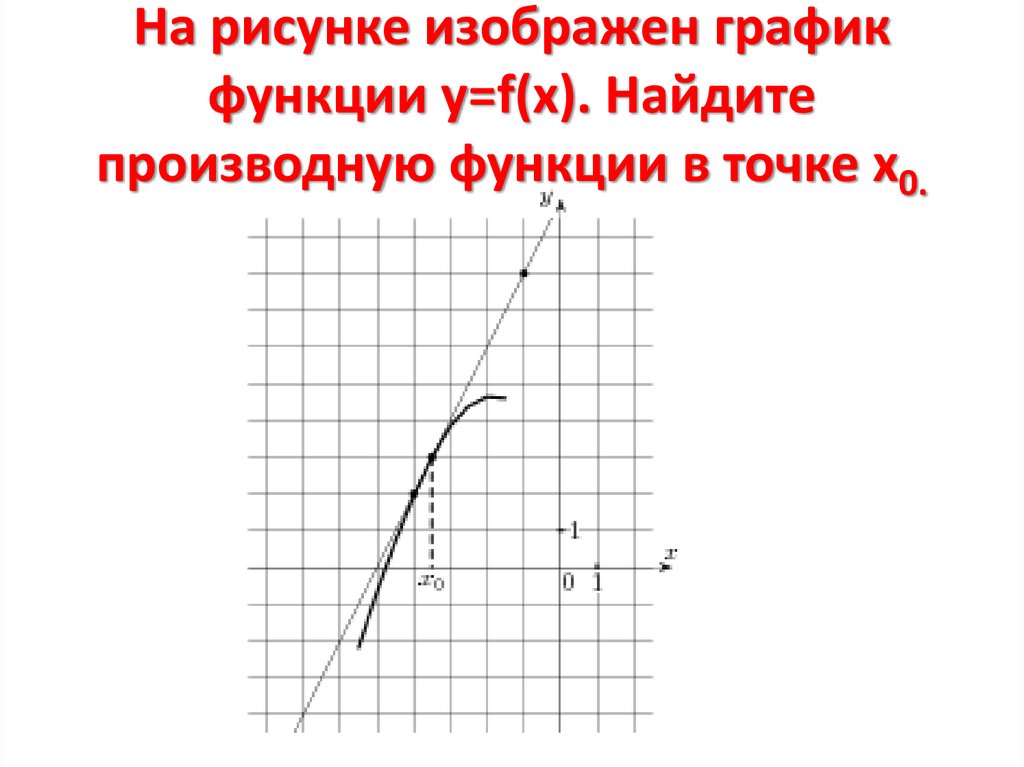
4. На рисунке изображен график функции у=f(x). Найдите производную функции в точке х0.

6
f x0 tg 1
6

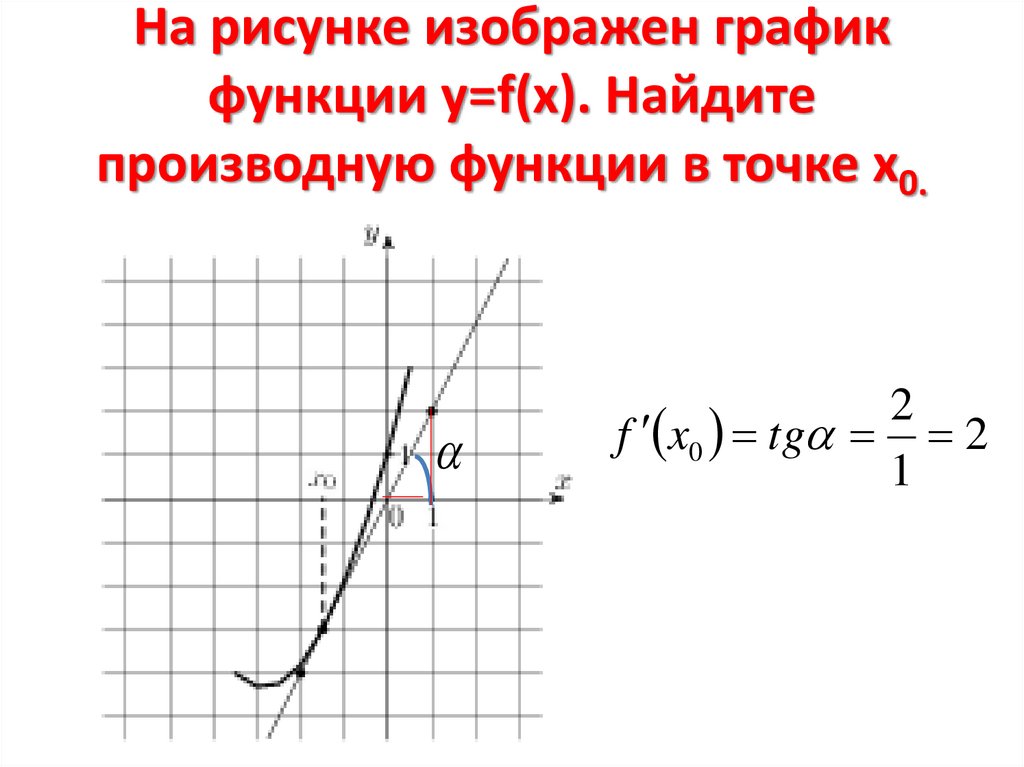
5. На рисунке изображен график функции у=f(x). Найдите производную функции в точке х0.

2
f x0 tg 2
1

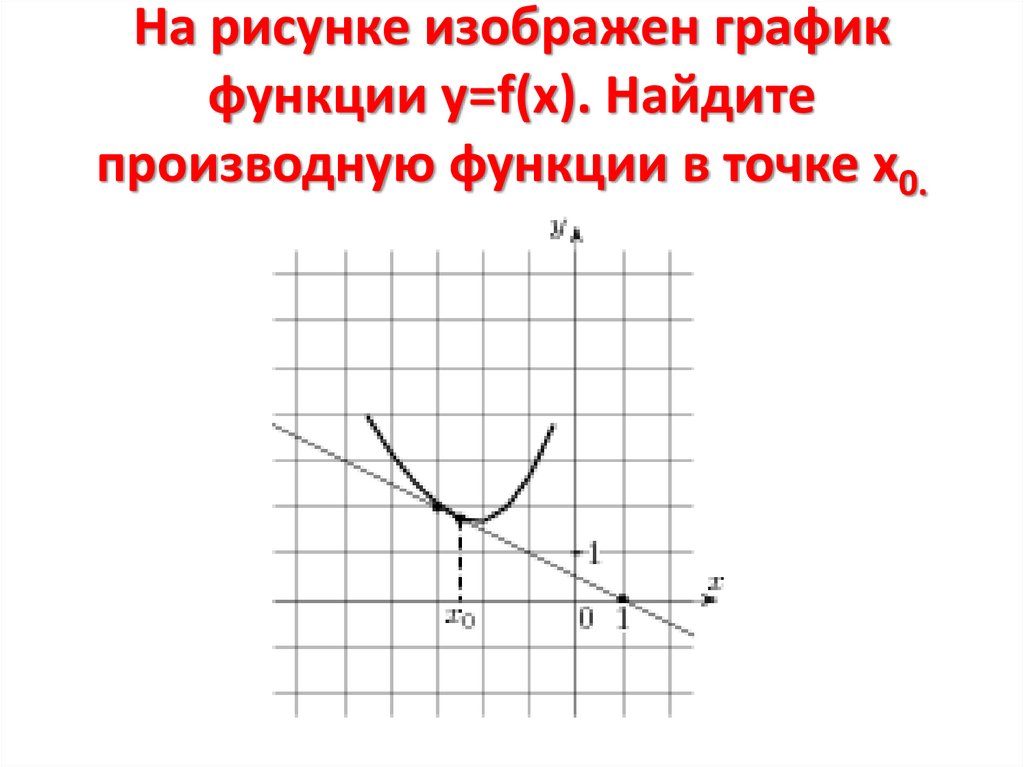
6. На рисунке изображен график функции у=f(x). Найдите производную функции в точке х0.

3
f x0 tg 0,5
6

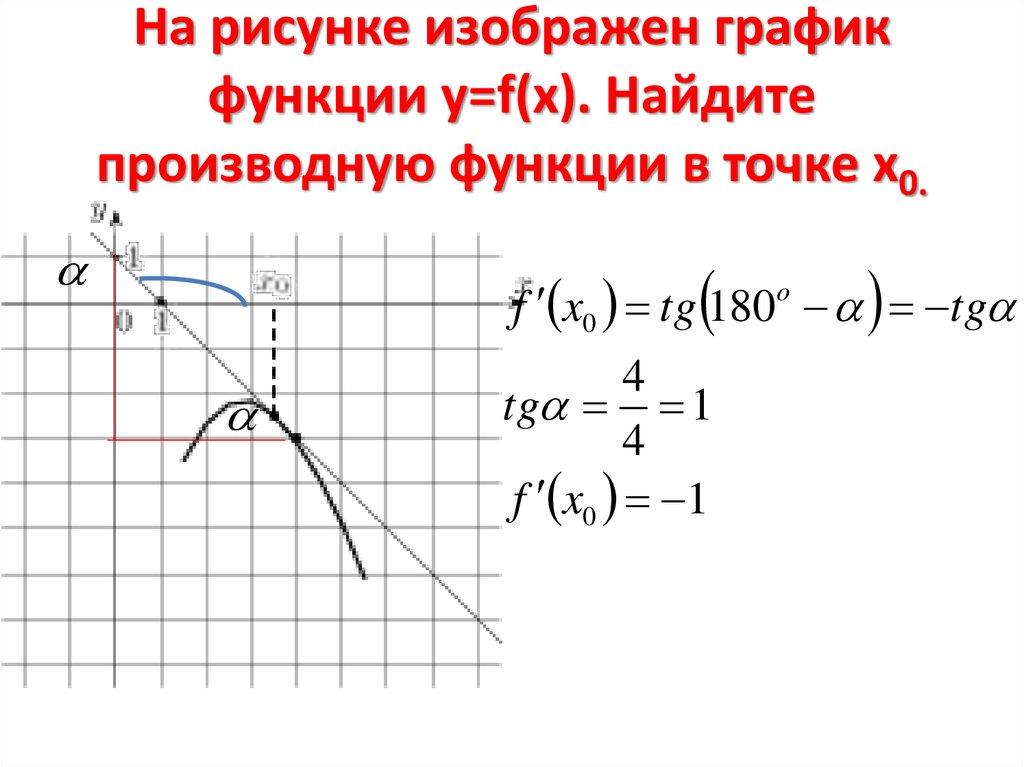
7. На рисунке изображен график функции у=f(x). Найдите производную функции в точке х0.

f x0 tg 180 tg
4
tg 1
4
f x0 1
o

8. На рисунке изображен график функции у=f(x). Найдите производную функции в точке х0.

f x0 tg 180o tg
3 1
tg
6 2
1
f x0
2

9. На рисунке изображен график функции у=f(x). Найдите производную функции в точке х0.

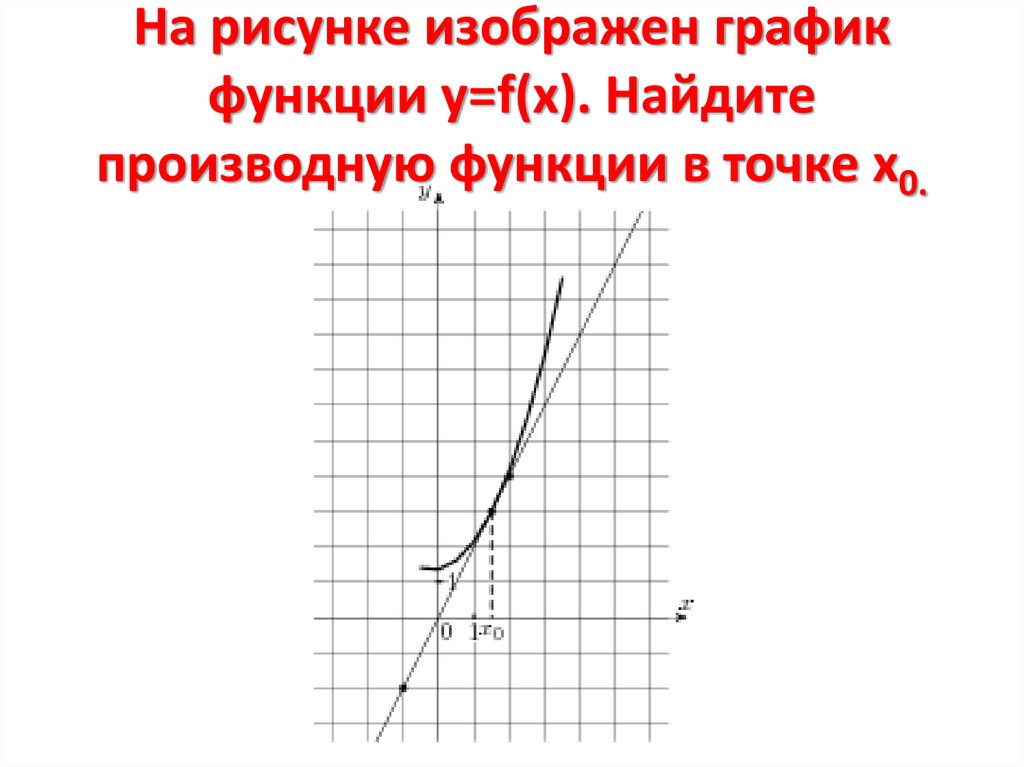
10. На рисунке изображен график функции у=f(x). Найдите производную функции в точке х0.

11. На рисунке изображен график функции у=f(x). Найдите производную функции в точке х0.

12. Ответы

• 1. 2
• 2. 2
• 3. -0,5

13. Определение производной

f x0 x f x
f
f ( x0 ) lim
lim
x 0 x
x 0
x
Найти производные по определению:
1). f x 3x 4;
2). f x x ;
1
3). f x ;
х
4). f x x
2

14. Определение производной

f x 3x 4;
Решение :
1. f f x f x0
f x0 3x0 4
f 3x 4 3x0 4 3x 4 3x0 4
3x 3x0 3 x x0 3 x
f
3 x
2. f ( x0 ) lim
lim
3.
x 0 x
x 0 x
3x 4 3

15. Определение производной

f x x ;
Решение :
2
1. f f x f x0
f x0 x0
2
f x x0 x x0 x x0
2
2
x x x0 x x0 x x0 x 2 x0 x
x 2 x0 x
f
2. f ( x0 ) lim
lim
2 x0
x 0 x
x 0
x
2
x 2x

16. Определение производной

f x х
Решение :
1. f f x f x0
f x0 x0
x x x x
f x x
0
x x0
0
2
x x0
x x0
2
x x0
x x0
f
2. f ( x0 ) lim
lim
x 0 x
x 0
x 2 x
1
0
x
x0 x x0
x
1
x0 x x0 x 2 x0

17. Определение производной

f x
Определение
производной
1
;
х
Решение :
1. f f x f x0 x0 x
1
f x0
x0
x0 x
x x0
1 1
x
f
x0 x x0 x0 x x0
x x0
x x0
f
x
1
2. f ( x0 ) lim
lim
2
x 0 x
x 0 x x x x
x0
0
0
1
1
2
x
x

18. Таблица производных

1. kx b k
2. x 1
3.C 0
2x
4. x
2
1
1
5. 2
x
x
1
6. x
2 x

19. Найдите производные по таблице

1. 4 x 6
4. 7
3
2. 10 x 2 5.
7
3. 4 8 x
6. ( 5 )
7. 5 x
5x
8.
2
4
x
9.
3
x

20. Найдите производные по таблице

1) 4 x 12
2) 6 3x
3) 0,9 x
4
4 ) х
3
3
x
5)
x
4
x
6) 5
x
7) 100
8) 0,8
9)

21. Ответы

1) 4 x 12 4
2) 6 3x 3
3) 0,9 x 0,9
4 4
4) х
3 3
3
x
5) 2 х
x
4
x
1
6) 5 2
х
x
7) 100 0
8) 0,8 0
9) 0

22. Проблема

2) 6 3 x х
1) 4 x 12 х
1
3) 5
х
2x 1
4)
3х 5

23. Правила дифференцирования

• Пусть u=u(x) и v=v(x) функции,
дифференцируемые в точке х0.
1. u v u v
2. u v u v v u
3. Cu Cu
u u v v u
4.
2
v
v

24. Правила дифференцирования

u
v
uI
u
v
uI v
1) 4 x 12 х 4 x 12
vI
х 4 2 х
1
u
vI
2) 6 3x х 6 3x х 6 3x х 3 х 6 3x
1
2 х
1
1
5
1
3) 5 5 5 2 2
х
х
х
х
2
x
1
2
x
1
3
х
5
2
x
1
3
х
5
2 3х 5 2 x 1 3
4)
2
2
3х 5
3х 5
3х 5
6 х 10 6 х 3
13
2
2
3х 5
3х 5

25. Найти производные, используя правила дифференцирования

1
1) 8 x
x
1
2) х
x
3) 6 х
2x 7
4)
4х 3

26. Производная степенной функции

x 1
х 2 х
х х х х х х х 1х х 2 х 3х
х
2
3
2
4
......
х
2
2
2
2

27. Таблица производных

х
1
х
sin x cos x tgx
f (x ) kx b x
C
x
f (x )
0
х
1
x
ln x log a x
k
1
f (x ) ctgx
e
x
1
f (x ) 2
sin x
x
e
a
x
a ln a
1
2
1
х
1
2
х х
cos x sin x
1
х ln a
1
cos 2 x