Введение кинематику. Кинематика точки

1.

А.И. Родионов
Теоретическая механика.
Ч.1. КИНЕМАТИКА

2.

Лекция 2.
Введение кинематику. Кинематика точки.
§2.1. Основные понятия.
Кинематика — раздел теоретической механики, в
котором механическое движение объектов природы и
техники, механические явления и процессы изучаются с
“геометрической” стороны, т.е. безотносительно к
взаимодействию этих объектов, причине изменения их
движения и т.д. Кинематика по-другому называется
хроногеометрией (геометрией во времени).
В кинематике строятся математические модели объектов
природы и техники, механических явлений и процессов
безотносительно к материальному составу этих объектов.

3.

§2.2. Аксиомы классической кинематики.
Кинематика – базируется на аксиомах классической
евклидовой геометрии, аксиомах о равномерном течении
времени и непрерывности Движения.
§2.3. Способы задания движения точки.
В кинематике как хроногеометрии движение точки должно
быть задано.
Движение точки считается заданным, если указан
способ, по которому определено ее положение в
пространстве в каждый момент времени.
Известны 3 способа задания движения точки: векторный,
координатный и естественный.

4.

§2.3.1. Векторный способ задания движения точки.
Векторный способ задания движения вытекает из физических
основ механики. Он связан с измерением отрезков и углов
(направлений). В силу этого этот способ практически не
применяется в ТМ для решения задач. В курсе ТМ к нему
обращаются в основном для определения кинематических
мер и для записи формул и т.д.
При векторном (физическом) способе задания движения
точки ей ставится в соответствие в каждый момент времени
её радиус-вектор относительно некоторого условного
неподвижного центра - полюса. Таким образом, радиус-вектор
является непрерывной векторной функцией аргумента t:
r r (t )
(1)

5.

t 0
l 0
e 0
вt
e t
l t
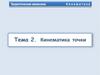
Рис.1.
Это означает, что в каждый момент движения
задаются
точки
как величина r=r(t),так и направление : e e (t) : r r (t )e (t ) , где
e (t ) 1 t

6.

У свободно движущейся точки число кинематически
независимых движений равно 3-м: по xyz. В связи с этим
говорят о 3-х степенях свободы (s) движения точки.
s = 1x+1y+1z=3
Таким образом, движение точки происходит в 3-х мерном
пространстве ее движений, совпадающем по размерности с 3х мерным пространством вещественных материальных форм,
называемом в современной науке просто пространством.

7.

§2.3.2.Траектория точки.
Точка в пространстве движется по траектории.
Траектория точки есть геометрическое место точек
пространства, которые последовательно во времени
проходит движущаяся точка. Говорят также, что
траектория точки есть годограф радиус-вектора.
В геометрии под годографом вектора понимают линию,
которую описывает его конец. Траектории бывают
разомкнутыми и замкнутыми. Разомкнутые имеют
начало при t=0. По замкнутым как правило движение
происходит по циклу. Заметим, что на разных участках
движения траектория может описываться разными
уравнениями.

8.

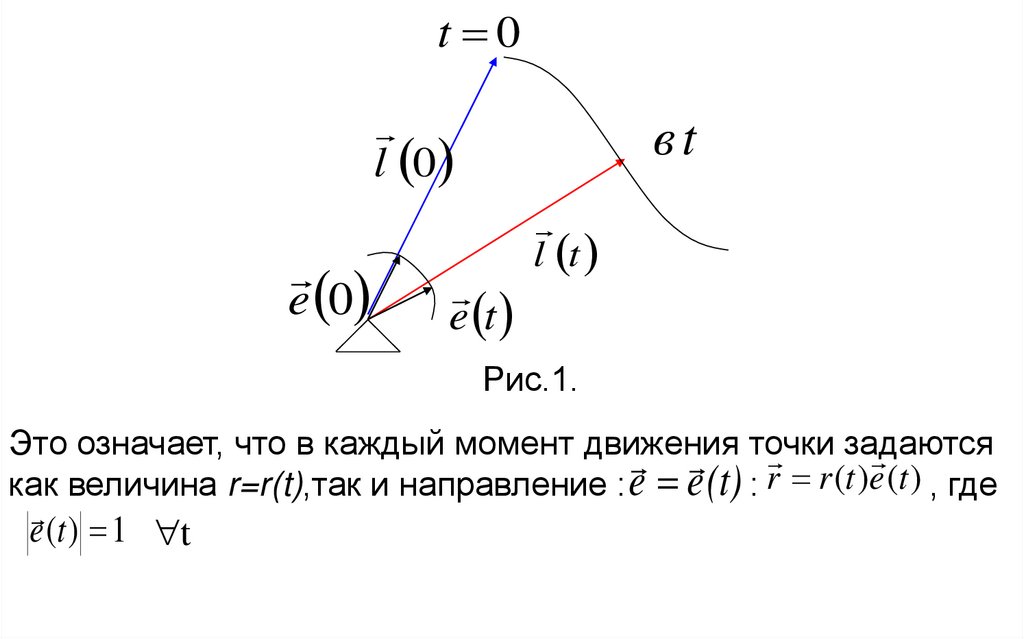
§2.3.3.Координатный способ.
При координатном способе с полюсом связывают какую-либо
систему ко ординат. Рассмотрим ниже в качестве примера
только декартовую и цилиндрическую (полярную) системы
координат
Рис. 2

9.

§2.3.3.1. Декартова система координат.
Декартовая система координат задается ее ортами — i , j , k
базисными векторами , которые не зависят от времени.
z
[i j ] k
[ j k ] i
[k i ] j
M ( 0)
M
k
0
j
y
i
x
Рис. 2а

10.

Радиус-вектор выражается через координаты точки x, y, z как
r xi yj zk
(2)
Движение точки считается заданным, если заданы
непрерывные функции
x x (t )
y y (t )
z z (t )
(3)
Совокупность зависимостей (3) определяет (задает) закон
движения точки.

11.

Приведем пример.
x x t 1t 2 2t 3
y y t 4 sin 5t
6t
z
z
t
1
e
Заметим, что коэффициенты 1,2,3,4,5,6 имеют размерность.
Причем каждый свою. Заметим также, что координаты точки x,
y, z в кинематике как хроногеометрии могут измеряться в
чём угодно: в см, м, и т.д. – это не имеет значения, и
определяется только условиями задачи.

12.

§2.3.3.2. Цилиндрическая система координат.
Цилиндрическая система координат
задается ортами 0 , p0 , k 0 ,
единичной длины | 0 | | p0 | | k0 | 1 t , которые
поворачиваются при движении точки, то есть являются
функциями времени: 0 0 (t ), p0 p0 (t ). При этом
[ 0 p0 ] k0 ,[ p0 k0 ] 0 ,[k0 p0 ] 0
Вектор 0 задает полярно-радиальное направление (ось), а
вектор p 0 – трансверсальное направление (ось), вектор k 0
во времени не изменяется и задает аксиальное направление
(ось). Положение точки в пространстве определяется
координатами: - полярным радиусом, - полярным углом, z
– координатой, аналогичной декартовой z.

13.

Движение точки в цилиндрической системе координат
считается заданным, если известны функции
(t )
(t )
z z (t )
(4)
r 0 zk0
(5)
Выражение (4) задает закон движения в цилиндрических
координатах.
Если же движение точки происходит на плоскости, то говорят
о полярной системе координат. При этом
(t )
, r r0
(t )
(6)

14.

§2.3.4. Определение траектории точки при координатном
способе задания её движения
Легко сообразить, что закон движения точки (3) или (4)
задает траекторию параметрически, где в качестве
параметра выступает время t. Поэтому траектория
движущейся точки может быть построена по циклическому
алгоритму:
1. задаем значение t = t1;
2. вычисляем значение x, y, z или , , z по формулам (3) или
(4);
3. возвращаемся к пункту 1);
4. и так до t = tn.

15.

Кроме того, уравнение траектории или уравнения траекторий
могут быть получены аналитически. Для этого необходимо
исключить параметр t из выражений системы (3).
В результате получится зависимость типа
(x, F y, z) = c
(7)
или F1(x, y) = c1, F2(x, z) = c2, F3(y, z) =c3.
Аналогично получим и для системы (4). Рассмотрим пример.
Пусть
x 2 cos 4t
y 2 sin 4t
z 2t
(8)

16.

Тогда в проекции на плоскость (X0Y) получим
В проекции на (X0Z):
x 2 y 2 22
(9)
x 2cos2z
(10)
А в проекции на плоскость (Y0Z):
y 2sin2z
(11)
Совокупность уравнений (8)…(11) задает траекторию точки,
которая является цилиндрической спиралью с шагом h = (м)
Рассмотрим другой пример. Пусть
x 10 cos 4 t
y 2 sin 4 t

17.

Тогда
2
2
x y
1
10 2
(12)
Уравнение (12) есть уравнение эллипса с полуосями = 10м, b
= 2м.
При любом другом законе движения поступаем аналогично.

18.

§2.3.5. Естественный способ задания движения точки.
Естественный или эйлеров (Leonard Eiler) способ задания
движения точки применяется чаще всего тогда, когда
заранее известна ее траектория движения. Это
имеет место особенно в задачах, связанных с техникой,
например, в редукторах, других механизмах. В этом
случае естественный способ является самым простым
и удобным для описания движения точки.
n
C
M
1
b
n
b
Рис. 3

19.

При естественном способе от точки-полюса вдоль траектории
откладывается дуговая координата S. Условно выбирается
положительное направление движения. Вводится связанный
с
движущейся точкой локальный декартов репер – , n , b
естественный трехгранник. Здесь
| | | n | | b | 1 t
[ n ] b , [n b ] , [b ] n
Касательный к траектории единичный вектор , задающий
положительное направление движения точки, называется
вектором тангенциали. Связанная с ним ось —
тангенциальной или же тангенциалью.

20.

Вектор нормали
, перпендикулярный , всегда направлен
на центр окружности кривизны, касательной к траектории в
данной точке.
Вектор бинормали перпендикулярен к векторам
и
.
Соответствующие им оси носят название нормали и
бинормали.
Рис. 4
n

21.

Векторы и n задают касательную или соприкасающуюся
плоскость (1), в которой лежит окружность кривизны,
касательная к траектории в данной точке. Векторы n и b
задают нормальную плоскость (2), а векторы и b —
спрямляющую плоскость (3). Полученный трехгранник,
составленный из касательной, нормальной и спрямляющей
плоскостей, называется естественным трехгранником.
Следует заметить, что окружности кривизны, касательные к
траектории в различных ее точках, — разные. Причем каждая
имеет свой радиус кривизны
(см. рис.5). При этом
кривизну (к) как меру определяют по формуле
к= 1/
(13)
Таким образом, например, кривизна прямой линии будет
равна к =1/ 0, а кривизна точки к. =1/0

22.

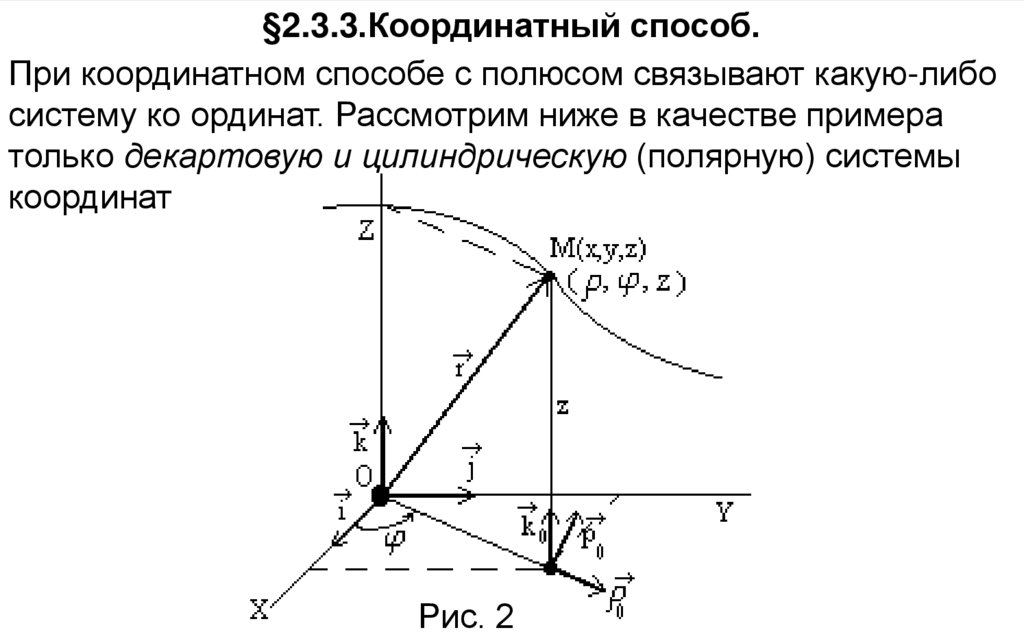
Как задается движение точки при естественном способе?
Здесь движение считается заданным, если явно задана
зависимость
(15)
S=S(t)
Рис. 15
При этом предполагается, что векторы , n , b зависят неявно от
времени. Это означает, что их производные по параметру t в
общем случае отличны от нуля. Зависимость (14) задает
закон движения точки. Например, так:
S 5t 2 e t cos S t cм