Серия независимых испытаний Бернулли. 10 класс

1.

23. Серия независимых
испытаний Бернулли
10 КЛАСС
С тат и с т и к а и т е о р и я в е р о я т н о с т и

2.

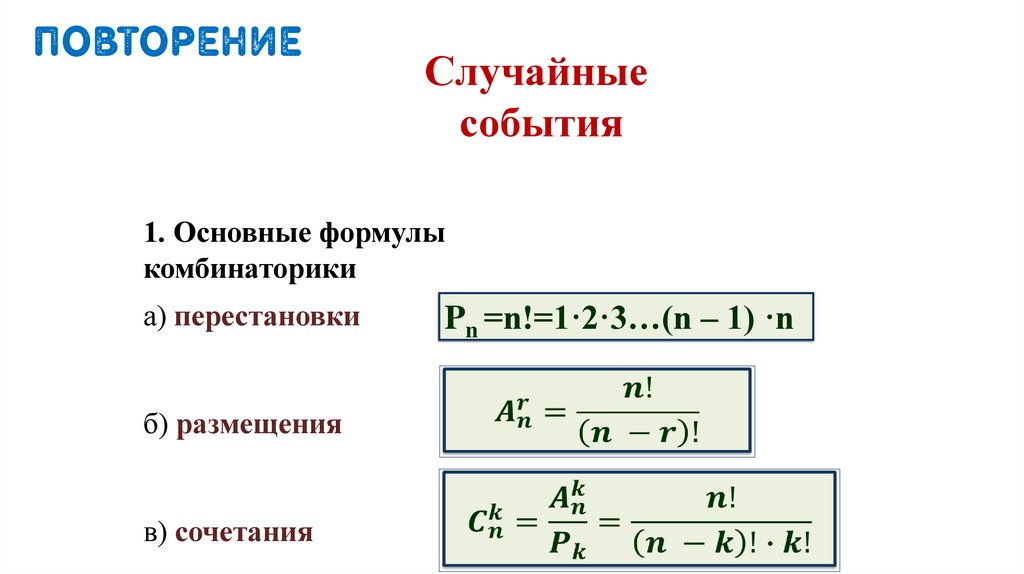
повторение
Случайные
события
1. Основные формулы
комбинаторики
а) перестановки
б) размещения
в) сочетания
Pn =n!=1·2·3…(n – 1) ·n

3.

повторение
2. Классическое
определение вероятности
, где m – число благоприятствующих
событию A исходов, n – число всех
элементарных равновозможных
исходов

4.

повторение
3. Вероятность суммы
событий
Теорема сложения вероятностей
несовместных событий:
Теорема сложения вероятностей
совместных событий: P(A+ B) = P(A) +P(B)−P(AB)

5.

повторение
Сочетания
Задача. Сколькими способам можно вывезти со склада 10
ящиков на двух автомашинах, если на каждую автомашину
грузят по 5 ящиков?
Решение. n=10, r = 5 , порядок не важен, повторений нет.
Нужна формула: Сочетания

6.

повторение
Размещения
Задача. Расписание одного дня состоит из 5 уроков.
Определить число вариантов расписания при выборе из
11 дисциплин.
Решение.
n =11, r = 5 , порядок важен (уроки идут по порядку),
повторений нет.
Нужна формула: Размещения

7.

повторение
Перестановки
Задача. Сколькими способами 4 человека могут
разместиться в четырехместном купе?
Решение.
n = 4, r = 4 , порядок важен (места в купе различны),
нужно выбрать все объекты, повторений нет.
Нужна формула: Перестановки
Pn = n!

8.

повторение
Независимые испытания. Формула Бернулли
При решении вероятностных задач часто приходится
сталкиваться с ситуациями, в которых одно и тоже
испытание повторяется многократно и исход каждого
испытания независим от исходов других. Такой
эксперимент еще называется схемой повторных
независимых испытаний или схемой Бернулли.

9.

Независимые испытания. Формула Бернулли
1) многократное извлечение из урны
одного шара при условии, что вынутый
шар после регистрации его цвета
кладется обратно в урну;
2) повторение одним стрелком
выстрелов по одной и той же
мишени при условии, что
вероятность удачного
попадания при каждом
выстреле принимается
одинаковой

10.

Независимые испытания. Формула Бернулли
Проведем n испытаний Бернулли. Это означает, что
все n испытаний независимы; вероятность появления
события А в каждом отдельно взятом или единичном
испытании постоянна и от испытания к испытанию не
изменяется (т.е. испытания проводятся в одинаковых
условиях).
А

11.

Независимые испытания. Формула Бернулли
Сумма вероятностей всегда равна 1.
Тогда вероятность того, что событие А появится в
этих n испытаниях ровно k раз, выражается формулой
Бернулли
Распределение числа успехов (появлений события) носит
название биномиального распределения.

12.

Формула Бернулли
вероятность появления события ровно k раз при n независимых
испытаниях, p - вероятность появления события при одном
испытании.

13.

Задание 1.
(Округлите до сотых)
Монету подбрасывают 5 раз. Какова
вероятность того, что герб выпадет
ровно 3 раза?

14.

Задание 2.
(Округлите до сотых) Вероятность
попадания стрелка в мишень при одном
выстреле равна 0,8. Стрелок делает 4
выстрела. Какова вероятность того, что
он попадет в мишень ровно 2 раза?

15.

Задание 3.
(Округлите до сотых) В партии из 10
деталей 2 бракованные. Наугад выбирают
3 детали. Какова вероятность того, что
среди них окажется ровно 1 бракованная?
(Считаем, что выбор происходит с
возвращением)

16.

Задание 4.
(Округлите до сотых) Игральную кость
бросают 6 раз. Какова вероятность того, что
шестерка выпадет не более 1 раза?

17.

Задание 5.
(Округлите до сотых) Вероятность того,
что покупатель выберет определенный
товар в магазине, равна 0,3. В магазин
зашли 5 покупателей. Какова вероятность
того, что товар выберут ровно 2
покупателя?

18.

Задание 6.
(Округлите до сотых) Проводится 7
независимых испытаний, в каждом из
которых вероятность успеха равна
0,6. Какова вероятность того, что
произойдет от 4 до 6 успехов
включительно?

19.

Задание 7.
(Округлите до сотых) Производится 8
независимых испытаний, в каждом из
которых вероятность успеха равна 0,7.
Какова
вероятность
того,
что
произойдет не менее 6 успехов?

20.

Задание 8.
(Округлите до сотых) В некотором
городе 20% населения имеют высшее
образование.
Случайным
образом
выбирают 6 человек. Какова вероятность
того, что высшее образование имеют
ровно 3 из них?

21.

Задание 9.
(Округлите до сотых) Вероятность того, что
студент сдаст экзамен, равна 0,75. Какова
вероятность того, что из 4 студентов,
сдающих экзамен, хотя бы 2 сдадут его?

22.

Задание 10.
(Округлите до сотых) Рабочий обслуживает 4 станка.
Вероятность того, что станок потребует внимания
рабочего в течение часа, равна 0,2. Какова вероятность
того, что в течение часа ровно два станка потребуют
внимания рабочего?

23.

Домашнее задание
Задание 1. (Округлите до сотых) В урне 6 белых и 4 черных шара. Из урны
5 раз извлекают шар, каждый раз возвращая его обратно. Какова
вероятность, что ровно 3 раза вынут белый шар?
Задание 2. (Округлите до сотых) Баскетболист совершает 6 бросков по
кольцу. Вероятность попадания при каждом броске равна 0,7. Найти
вероятность, что он попадет в кольцо не менее 4 раз.
Задание 3. (Округлите до сотых) Вероятность того, что при одном
измерении некоторой физической величины произойдет ошибка, равна 0,1.
Произведено 10 независимых измерений. Найти вероятность того, что не
более двух измерений будут содержать ошибку.