Similar presentations:
Замечательные точки и отрезки треугольника
1.
З А М Е Ч АТ Е Л Ь Н Ы ЕТОЧКИ И ОТРЕЗКИ
ТРЕУГОЛЬНИКА
2.
7.1.1.15 сравнивать расположение высот востроугольном, прямоугольном и тупоугольном
треугольниках;
9.1.2.6 знать и применять свойства медиан
треугольника;
9.1.4.16 знать и применять свойство биссектрисы
треугольника;
2/18/2025
Sample Footer Text
2
3.
H T T P : / / L E A R N I N G A P P S . O R G / WAT C H ? V=P38BRTVXN17
4.
ТЕРМИНОЛОГИЯ• Altitude – высота
• Bisector - биссектриса
• Median – медиана
• Measure - величина, мера
• Angle – угол
• Value – значение
5.
ЗАДАНИЕ 1.Архитектор планирует построить парк развлечений в пределах легкого
доступа от трех крупнейших городов в этом районе, как показано на карте
ниже. Архитектор должен принять решение с ABC Construction Company о
наилучшем местонахождении для парка развлечения, чтобы
минимизировать затраты там, где это возможно.
Дороги должны быть построены непосредственно к городам или к
существующим автомагистралям независимо от того, где расположен парк
развлечений.
6.
Обратите внимание на карту и выберитеместо, которое, по вашему мнению, будет
лучше всего для создания парка
развлечения. Обоснуйте свой ответ.
7.
Какую точку Вы рекомендуете дляместонахождение парка
развлечения?
8.
КОНСПЕК Т_СХЕМА ДЛЯ ЗАПОЛНЕНИЯ9.
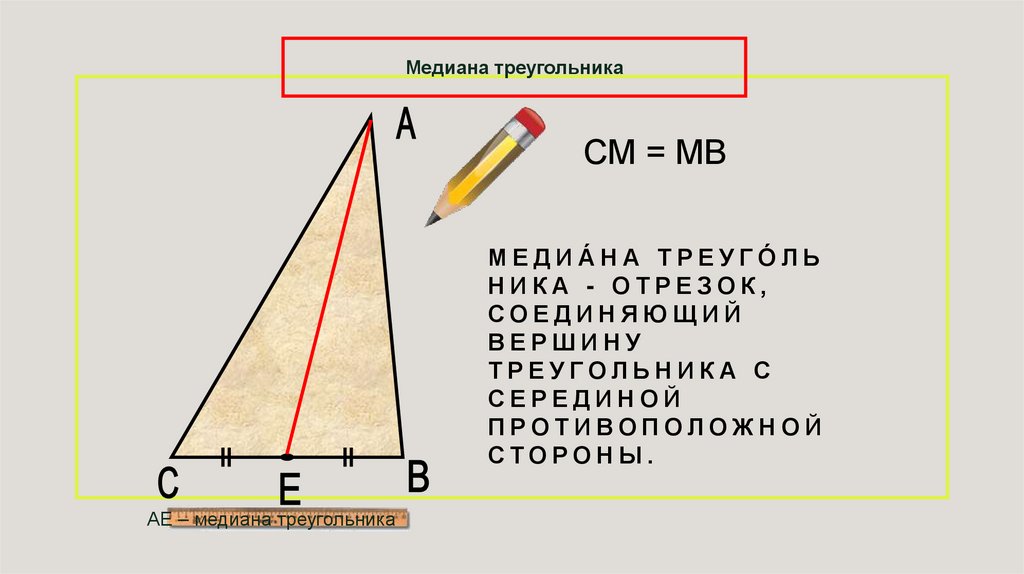
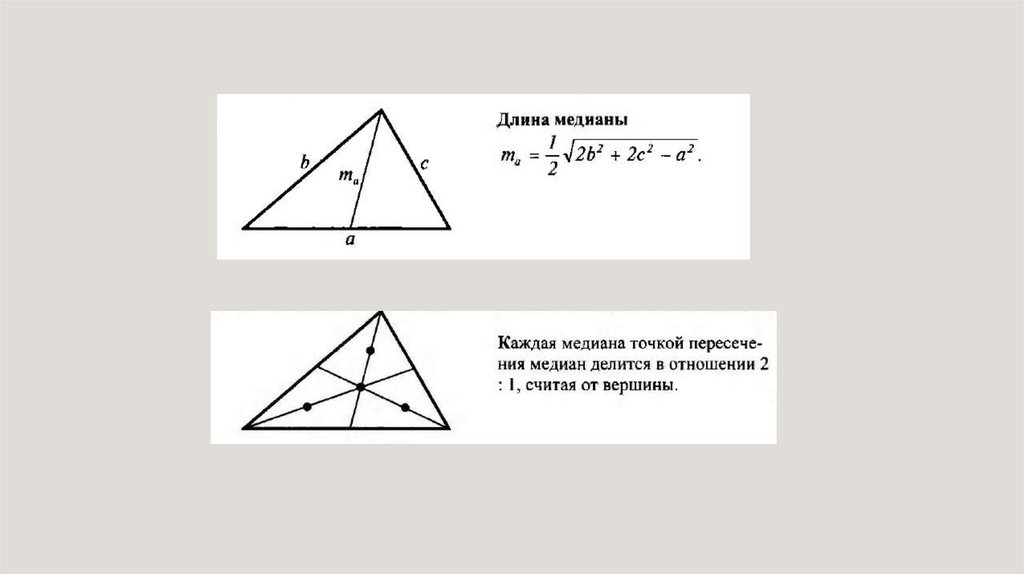
Медиана треугольникаСМ = МВ
М Е Д И А́ Н А Т Р Е У Г О́ Л Ь
НИКА - ОТРЕЗОК,
СОЕДИНЯЮЩИЙ
ВЕРШИНУ
ТРЕУГОЛЬНИКА С
СЕРЕДИНОЙ
ПРОТИВОПОЛОЖНОЙ
СТОРОНЫ.
АЕ – медиана треугольника
10.
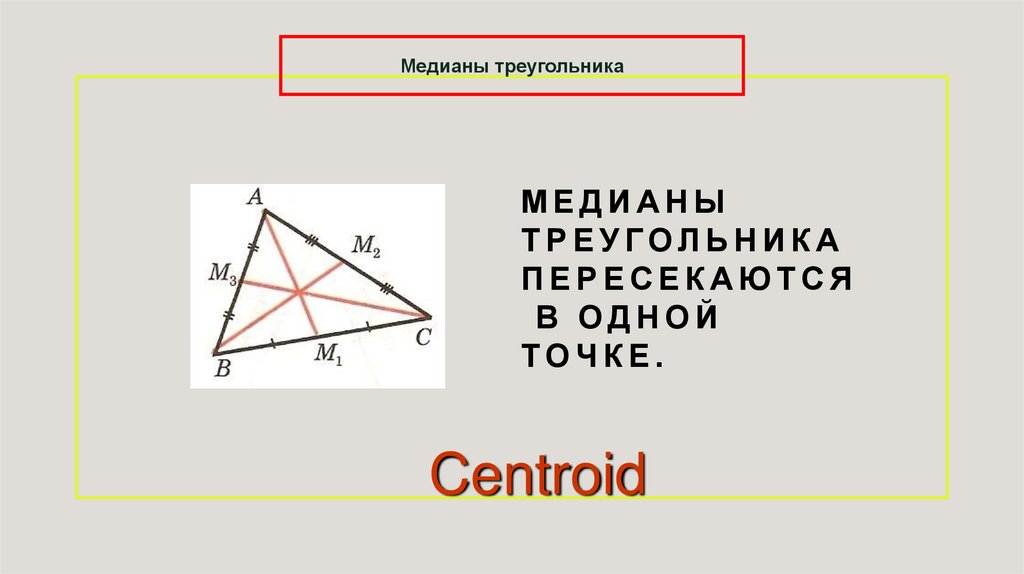
Медианы треугольникаМЕДИАНЫ
ТРЕУГОЛЬНИКА
ПЕРЕСЕКАЮТСЯ
В ОДНОЙ
ТОЧКЕ.
Centroid
11.
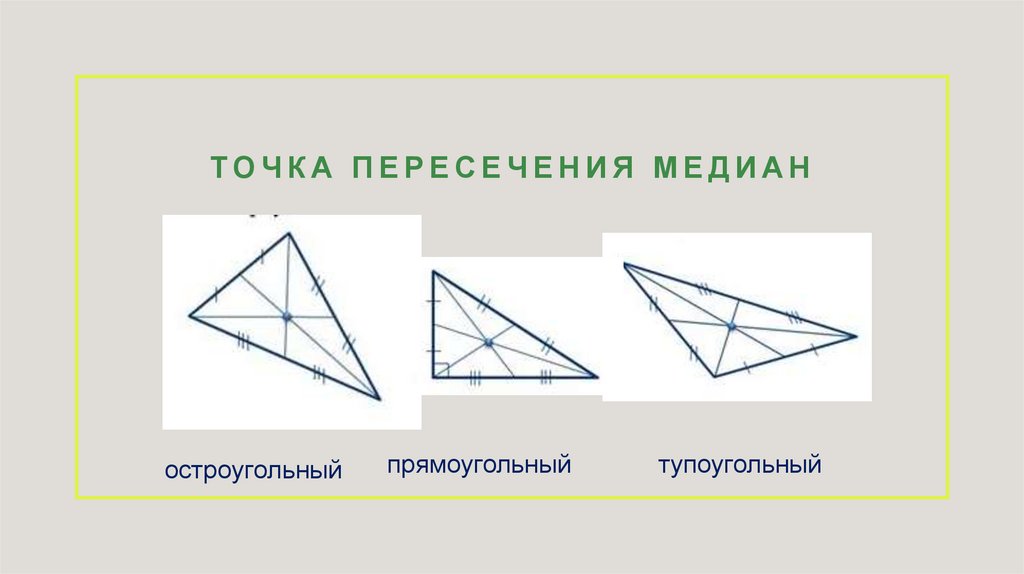
ТОЧКА ПЕРЕСЕЧЕНИЯ МЕДИАНостроугольный
прямоугольный
тупоугольный
12.
Центр тяжести13.
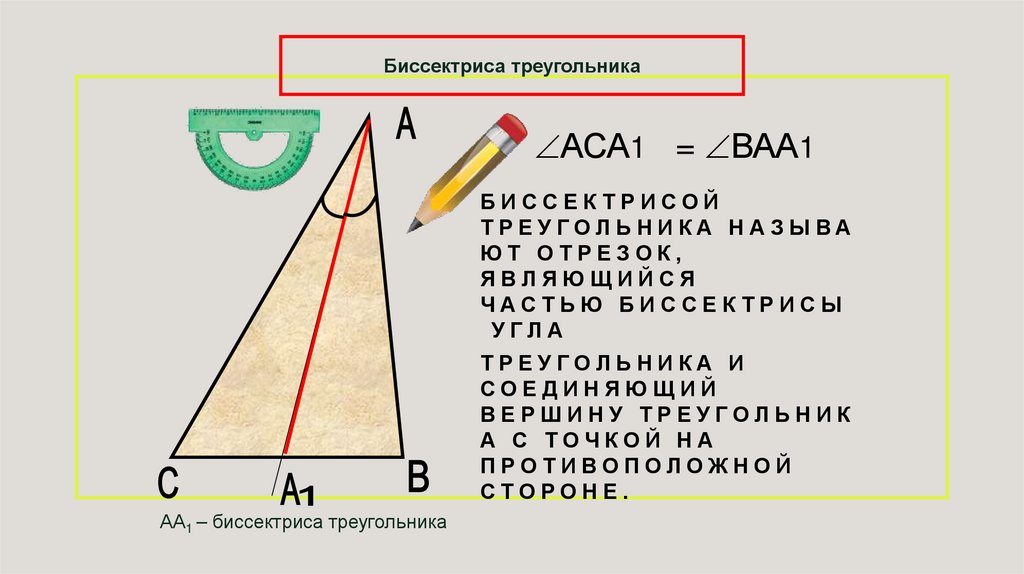
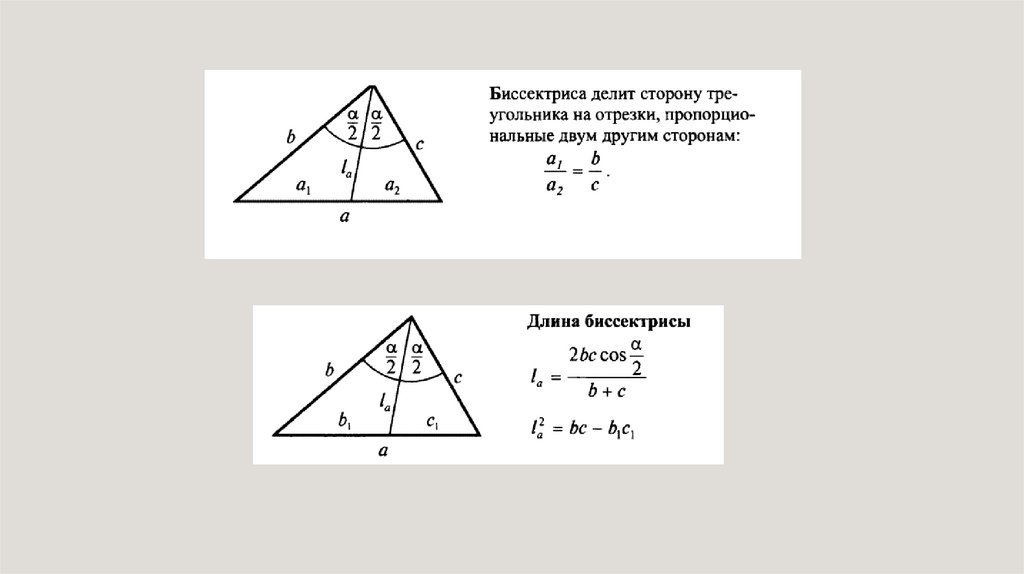
Биссектриса треугольникаАСА1 = ВАА1
БИССЕКТРИСОЙ
ТРЕУГОЛЬНИКА НАЗЫВА
ЮТ ОТРЕЗОК,
ЯВЛЯЮЩИЙСЯ
ЧАСТЬЮ БИССЕКТРИСЫ
УГЛА
ТРЕУГОЛЬНИКА И
СОЕДИНЯЮЩИЙ
ВЕРШИНУ ТРЕУГОЛЬНИК
А С ТОЧКОЙ НА
ПРОТИВОПОЛОЖНОЙ
СТОРОНЕ.
АА1 – биссектриса треугольника
14.
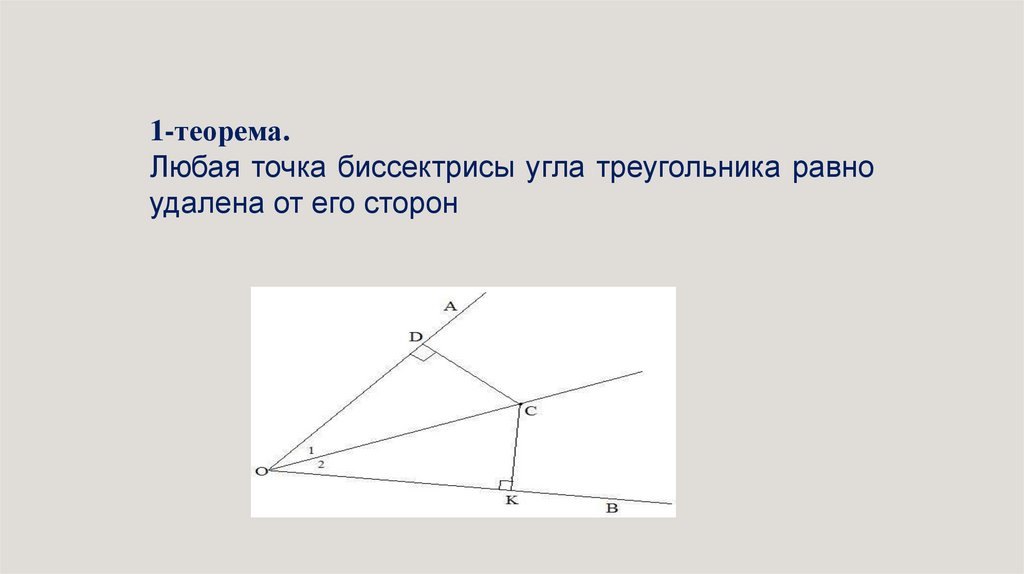
1-теорема.Любая точка биссектрисы угла треугольника равно
удалена от его сторон
15.
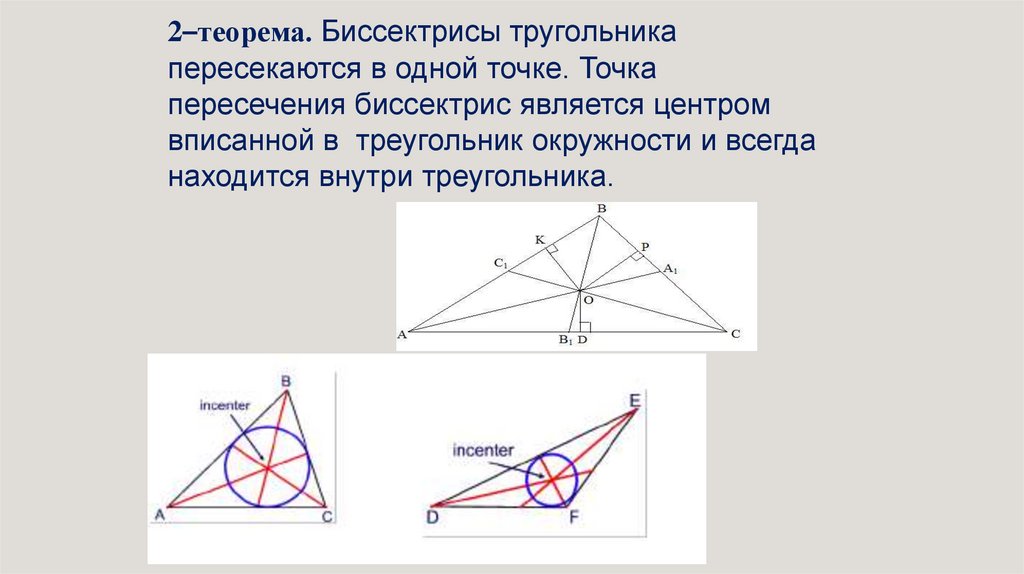
2–теорема. Биссектрисы тругольникапересекаются в одной точке. Точка
пересечения биссектрис является центром
вписанной в треугольник окружности и всегда
находится внутри треугольника.
16.
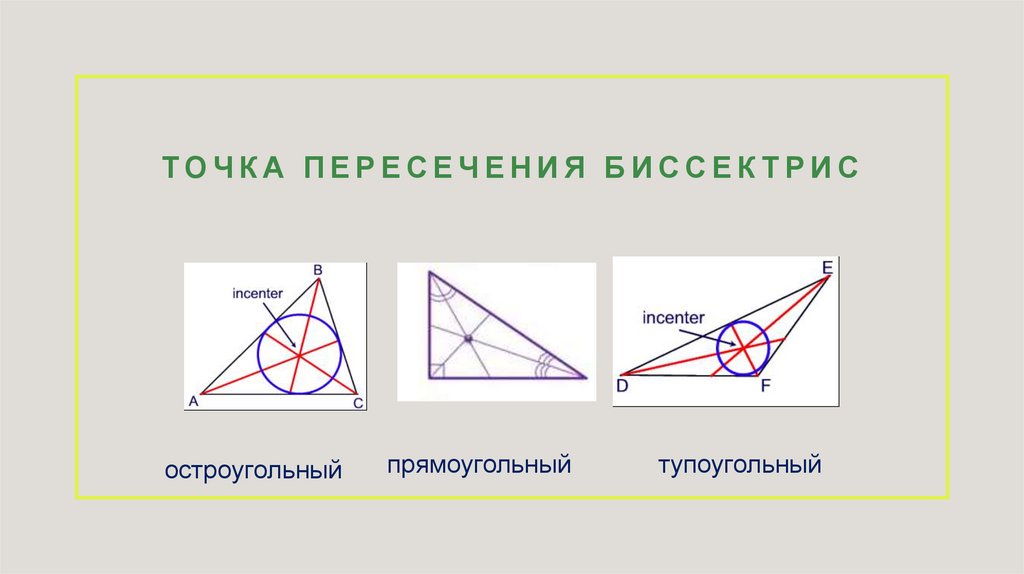
ТОЧКА ПЕРЕСЕЧЕНИЯ БИССЕК ТРИСостроугольный
прямоугольный
тупоугольный
17.
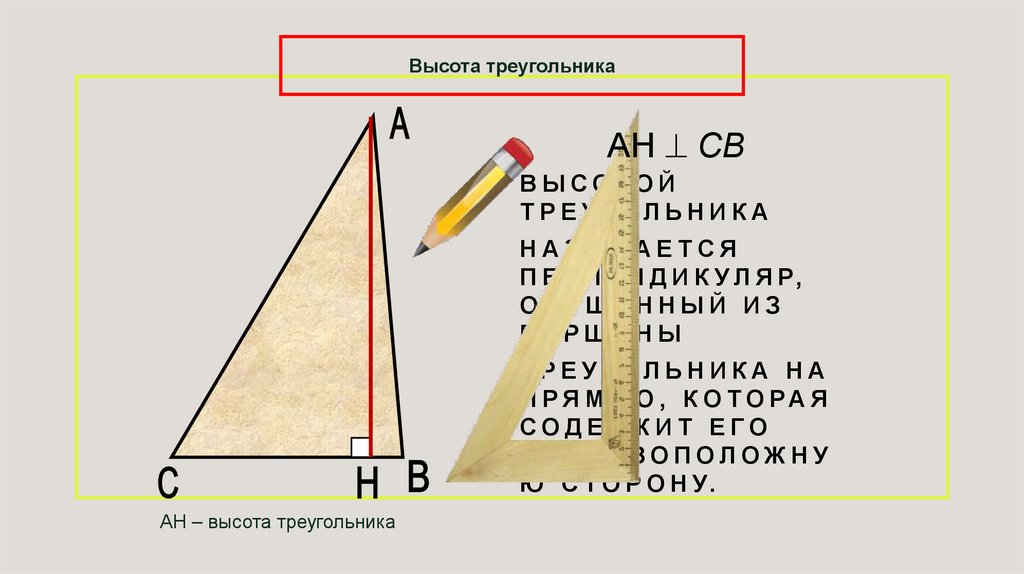
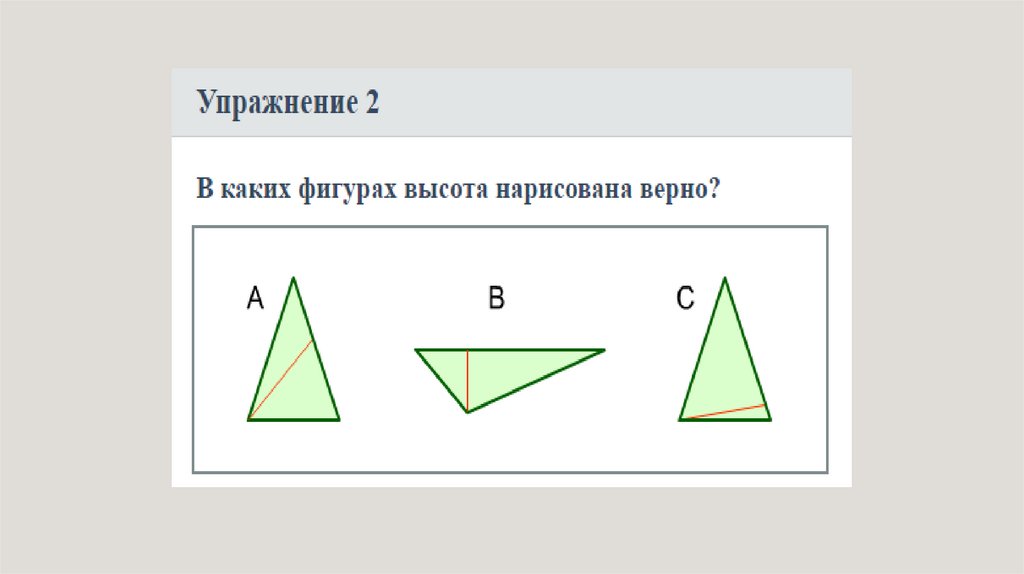
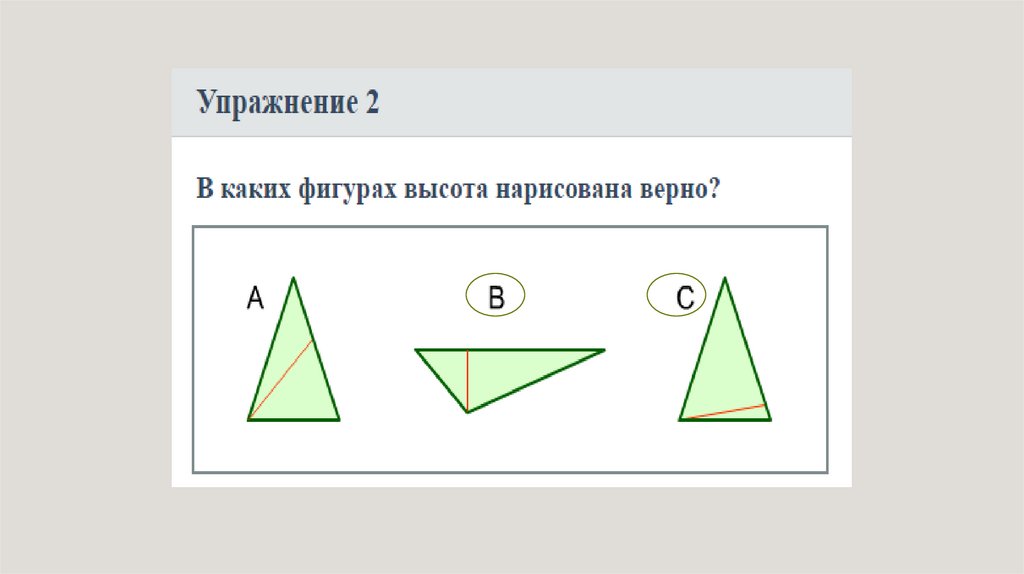
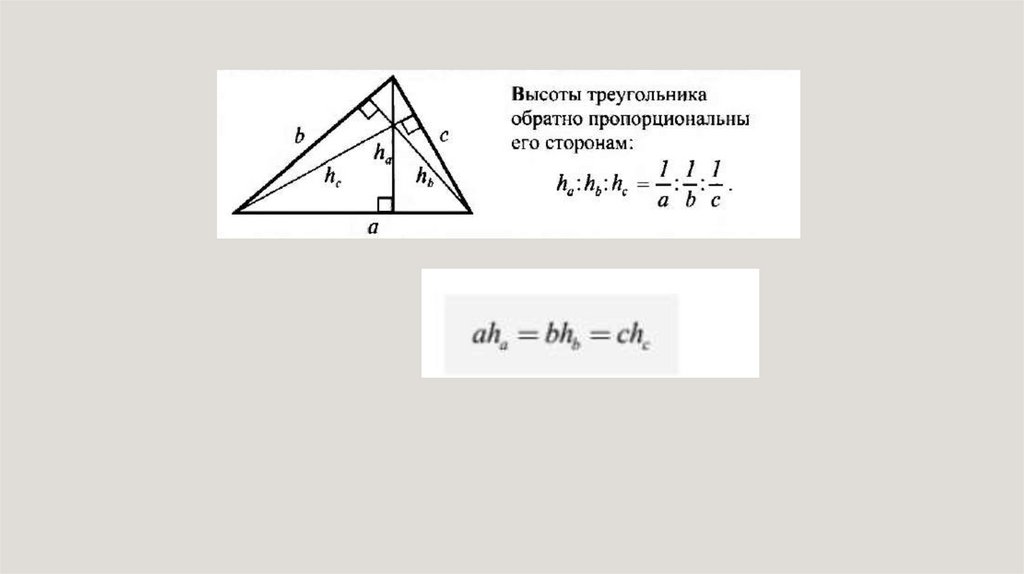
Высота треугольникаАН СВ
ВЫСОТОЙ
ТРЕУГОЛЬНИКА
НАЗЫВАЕТСЯ
П Е Р П Е Н Д И К У Л Я Р,
ОПУЩЕННЫЙ ИЗ
ВЕРШИНЫ
ТРЕУГОЛЬНИКА НА
П Р Я М У Ю , К О Т О РА Я
СОДЕРЖИТ ЕГО
ПРОТИВОПОЛОЖНУ
Ю С Т О Р О Н У.
АН – высота треугольника
18.
5-теорема. Высоты треугольника или ихпродолжения пересекаются в одной
точке. Точку пересечения высот
называется ортоцентром треугольника.
19.
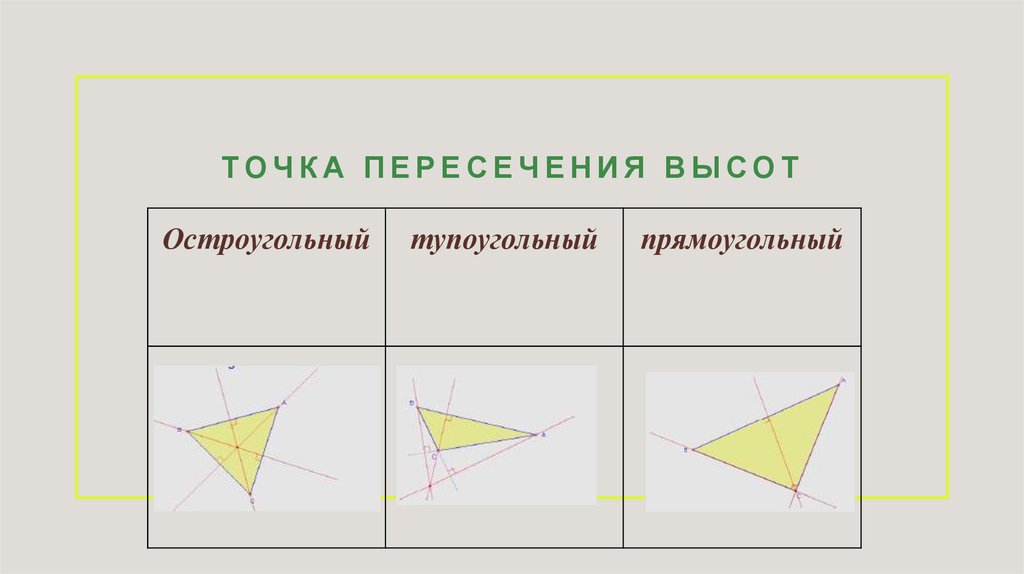
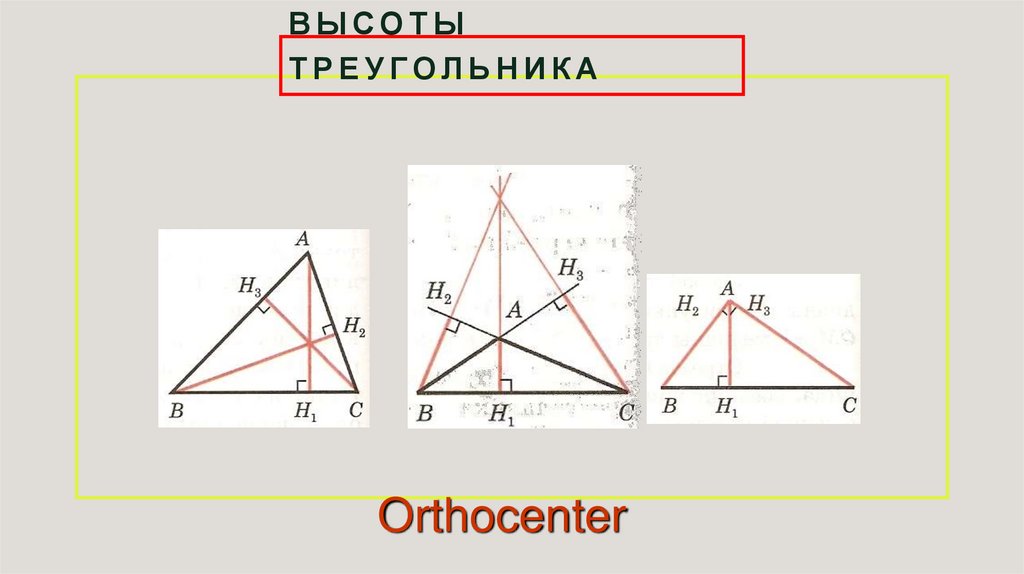
ТОЧКА ПЕРЕСЕЧЕНИЯ ВЫСОТОстроугольный
тупоугольный
прямоугольный
20.
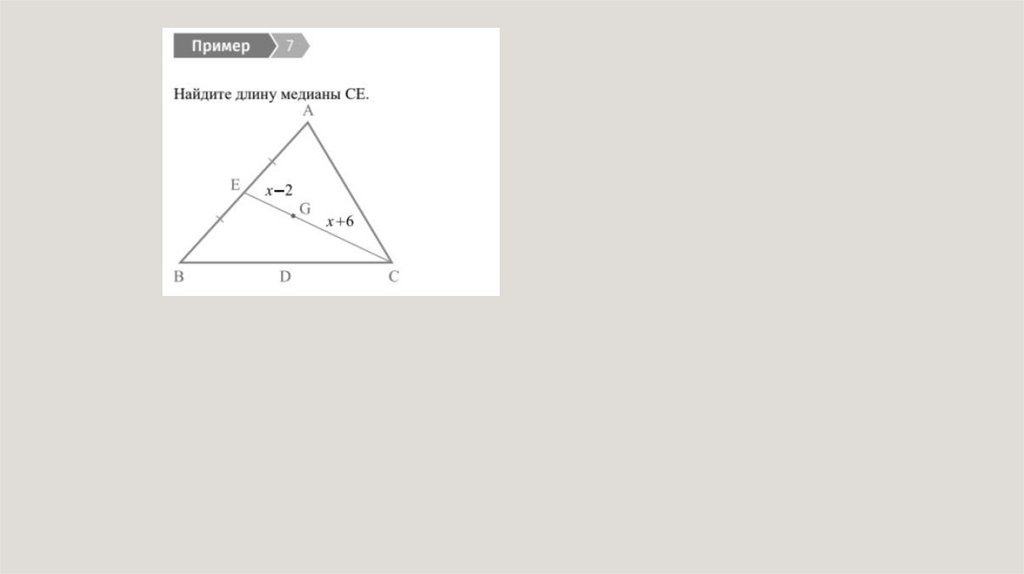
21.
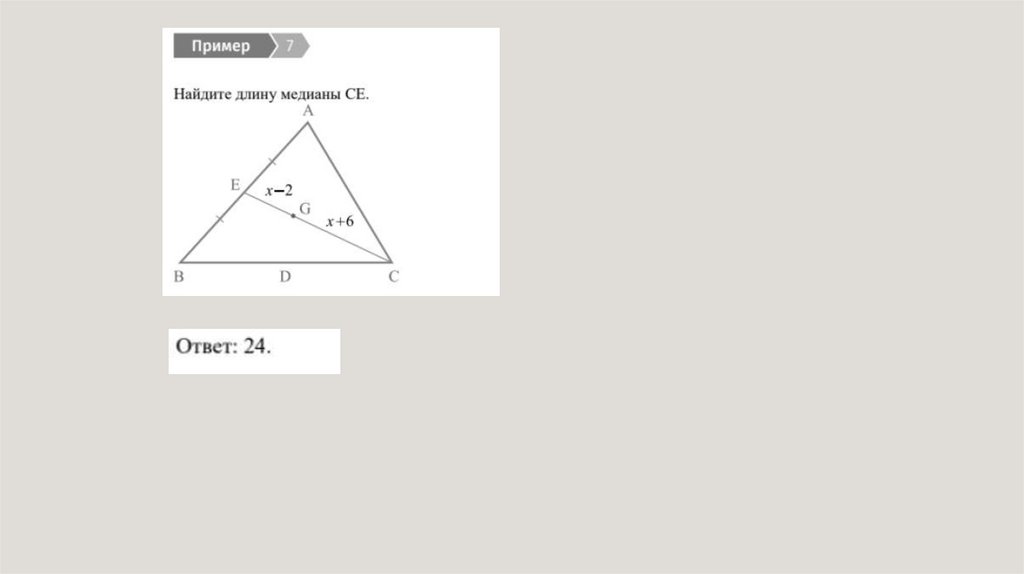
22.
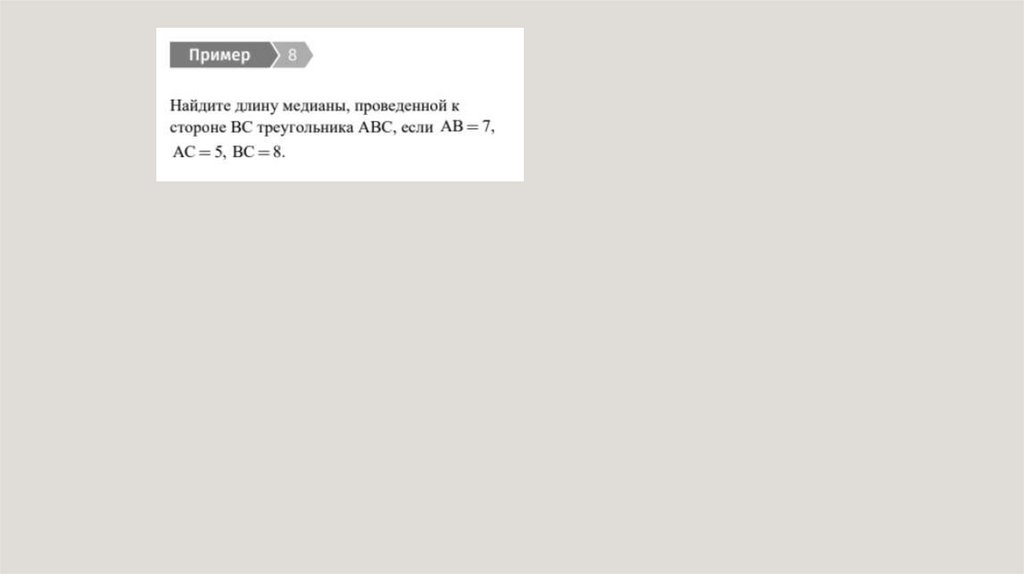
23.
24.
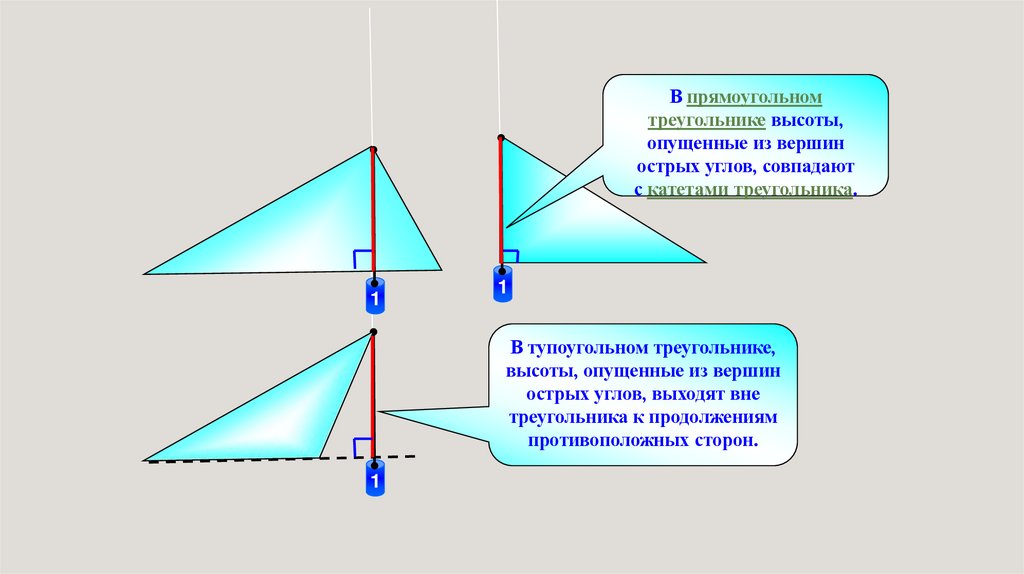
В прямоугольномтреугольнике высоты,
опущенные из вершин
острых углов, совпадают
с катетами треугольника.
1
1
В тупоугольном треугольнике,
высоты, опущенные из вершин
острых углов, выходят вне
треугольника к продолжениям
противоположных сторон.
1
25.
ВЫСОТЫТРЕУГОЛЬНИКА
Orthocenter
26.
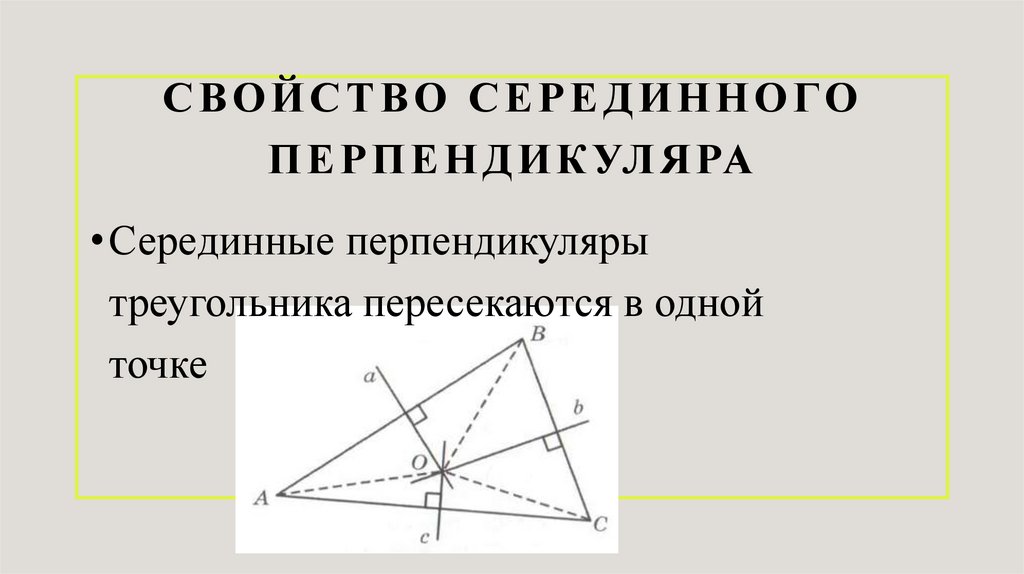
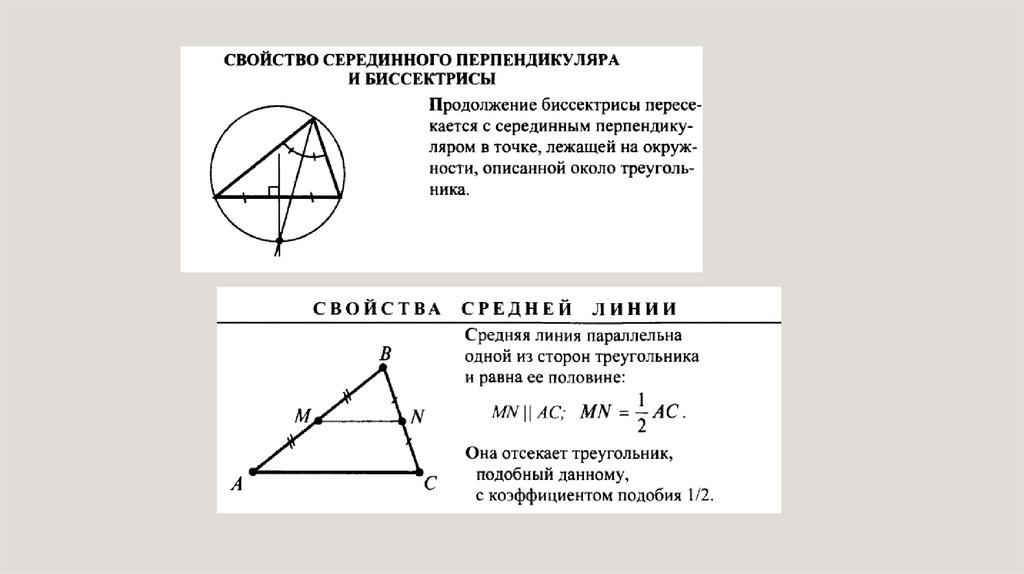
СВОЙСТВО СЕРЕДИННОГОП Е Р П Е Н Д И К УЛ Я РА
• Серединные перпендикуляры
треугольника пересекаются в одной
точке
27.
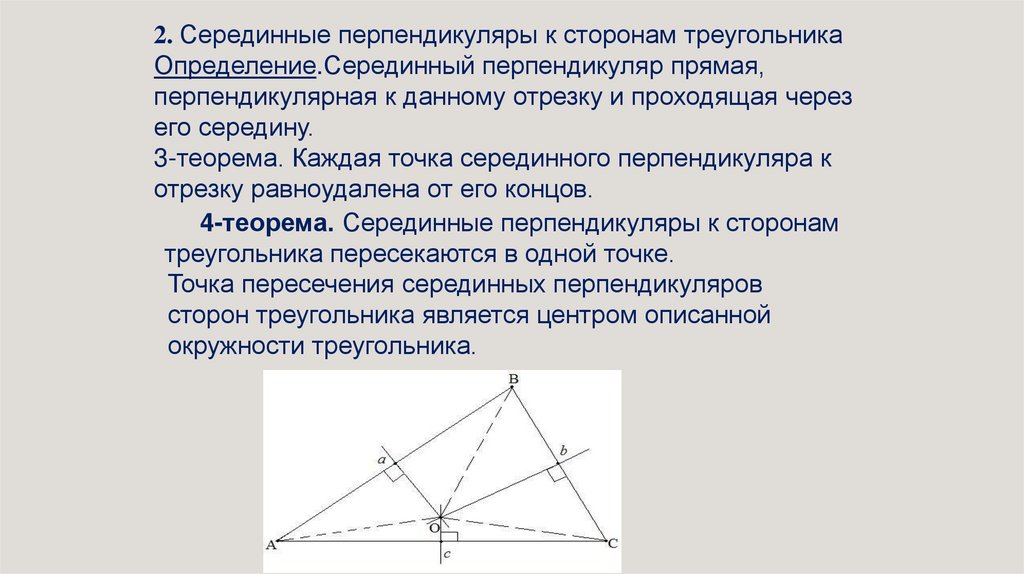
2. Серединные перпендикуляры к сторонам треугольникаОпределение.Серединный перпендикуляр прямая,
перпендикулярная к данному отрезку и проходящая через
его середину.
3-теорема. Каждая точка серединного перпендикуляра к
отрезку равноудалена от его концов.
4-теорема. Серединные перпендикуляры к сторонам
треугольника пересекаются в одной точке.
Точка пересечения серединных перпендикуляров
сторон треугольника является центром описанной
окружности треугольника.
28.
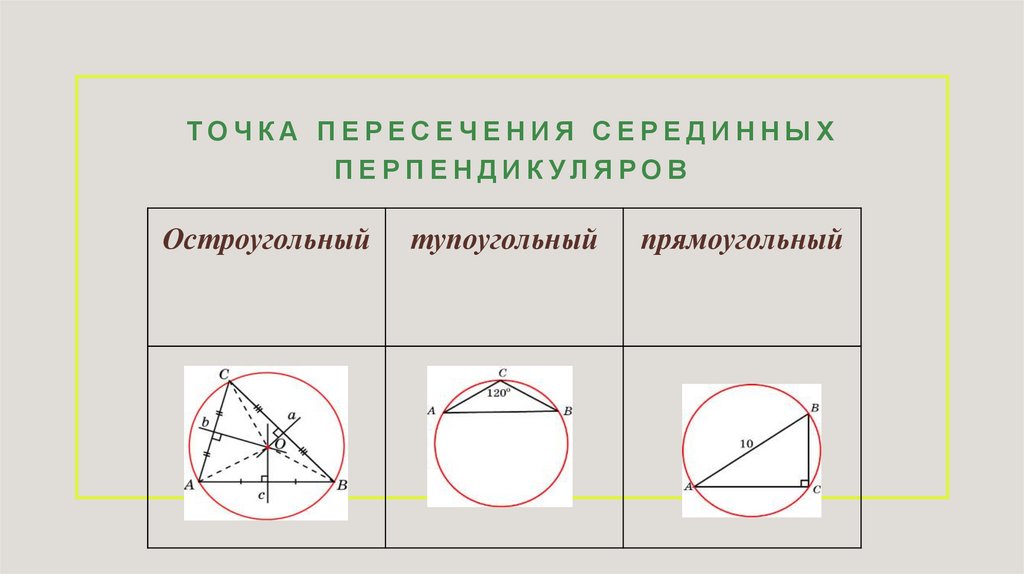
ТОЧКА ПЕРЕСЕЧЕНИЯ СЕРЕДИННЫХПЕРПЕНДИК УЛЯРОВ
Остроугольный
тупоугольный
прямоугольный
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
РЕФЛЕКСИЯЧто я знал(а) раньше
Что я узнал(а)
О чем мне нельзя забывать




























 mathematics
mathematics








